Class 6 Understanding Elementary Shape Extra Questions
Understanding Elementary Shape Class 6 Extra Questions Very Short Answer Type
Question 1.
Which of the following line-segments is longer?
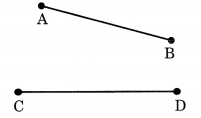
Solution:
By using divider, \(\overline { CD }\) seems to be longer than \(\overline { AB }\) .
Question 2.
How many line segments are used in making a triangle?
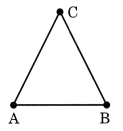
Solution:
Three line segments are used to make a triangle.
Question 3.
What is the measure of straight angle?
Solution:
The measure of straight angle is 180°.
Question 4.
What is complete angle?
Solution:
The angle for one revolution is called a complete angle.
Question 5.
Find the number of right angle turned through by the hour hand of a clock when it goes from 3 to 6.
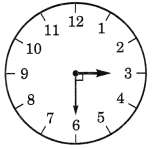
Solution:
When the hour hand of a clock goes from 3 to 6, it turns through a right angle.
Question 6.
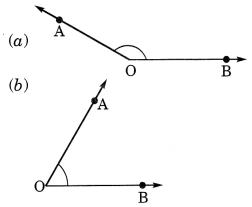
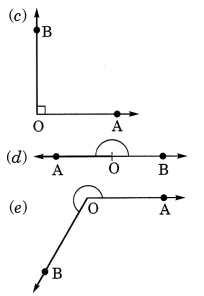
Draw the rough sketch of the following:
(a) Acute angle
(b) Obtuse angle
(c) Reflex angle
Solution:
(a) Acute angle
(b) Obtuse angle
(c) Reflex angle
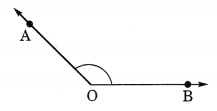
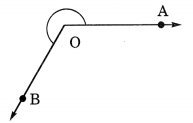
Question 7.
Identify the types of angle from the given figures:
Solution:
(a) Obtuse angle
(b) Acute angle
(c) Right angle
(d) Straight angle
(e) Reflex angle
Question 8.
What are the degree measures of the following angles?
(a) Right angle
(b) A complete angle
(c) Straight angle
Solution:
(a) Degree measure of a right angle is 90°.
(b) Degree measure of a complete angle is 360°.
(c) Degree measure of a straight angle is 180°.
Question 9.
What are the types of the given triangles on the basis of angles?
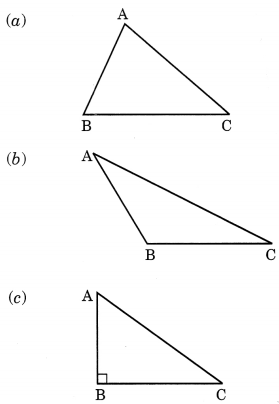
Solution:
(a) Acute angled triangle.
(b) Obtuse angled triangle.
(c) Right angled triangle.
Question 10.
What are the types of the following triangles on the basis of sides?
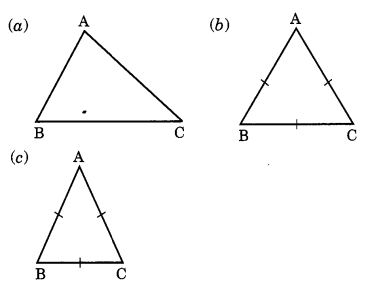
Solution:
(a) Scalene triangle.
(b) Equilateral triangle.
(c) Isosceles triangle.
Basic Geometrical Ideas Class 6 Extra Questions Short Answer Type
Question 11.
In the given figure, name the following angles as acute, obtuse, right, straight or reflex.
(a) ∠QOY
(b) ∠YOP
(c) ∠ROX
(d) ∠QOX
(e) ∠POQ
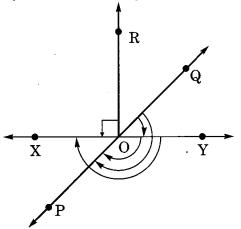
Solution:
(a) ∠QOY = acute angle.
(b) ∠YOP = obtuse angle.
(c) ∠ROX = right angle.
(d) ∠QOX = reflex angle.
(e) ∠POQ = straight angle.
Question 12.
In the given figure, find the measure of the angles marked with a, b, c, d, e and f.
Solution:
∠a = 180° -129° = 51°
∠b = 180° – (51° + 92°)
= 180° – 143° = 37°
∠c = 180° – 88° = 92°
∠d = 180° – 152° = 28°
∠e = 180° – 143° = 37°
∠f= 180° – (∠e + ∠d)
= 180° – (37° + 28°)
= 180°- 65°= 115°
∠g = 180° – ∠f = 180° – 115° = 65°
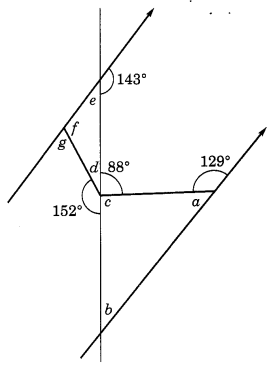
Question 13.
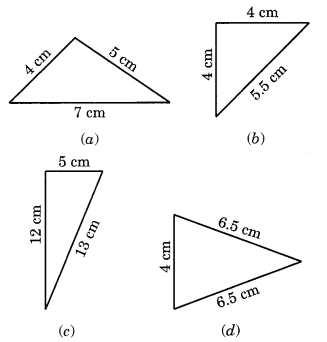
Classify the given triangles whose sides are indicated on them.
Solution:
(a) All sides are different. So, it is a scalene triangle.
(a) Lengths of two sides of the triangle are same. So, it is an isosceles triangle.
(b) All sides are unequal and one angle is right angle. So it is scalene right angled triangle.
(c) Two sides of this triangle are equal. So, it is an isosceles triangle.
Question 14.
Complete each of the following, so as to make a true statement:
(a) A ……….. is a rectangle with a pair of adjacent sides equal.
(b) A parallelogram with a pair of adjacent sides equal is called a ………. .
(c) A quadrilateral having exactly one pair of parallel sides is called a …….. .
(d) A quadrilateral having both pairs of opposite sides parallel, is called a ……… .
(e) A parallelogram whose each angle is a right angle is called a ………… .
Solution:
(a) Square
(b) Rhombus
(c) Trapezium
(d) Parallelogram
(e) Rectangle.
Basic Geometrical Ideas Class 6 Extra Questions Long Answer Type
Question 15.
Verify the ‘Euler’s formula’ V + F = E + 2 for the given figures.
(a) A triangular prism having 5 faces, 9 edges and 6 vertices.
(b) A rectangular prism with 6 faces, 12 edges and 8 vertices.
(c) A pentagonal prism with 7 faces, 15 edges and 10 vertices.
(d) A tetrahedron -with 4 faces, 6 edges and 4 vertices.
Solution:
(a) Here, F = 5, E = 9 and V = 6
∴ V + F = E + 2
⇒ 6 + 5 = 9 + 2
⇒ 11 = 11
Hence, verified.
(b) Here, F = 6, E = 12 and V = 8
∴ V + F = E + 2
⇒ 8 + 6 = 12 + 2
⇒ 14 = 14
Hence, verified.
(c) Here, F = 7, E = 15 and V = 10
∴ V + F = E + 2
⇒ 10 + 7 = 15 + 2
⇒ 17 = 17
Hence, verified.
(d) Here, F = 4, E = 6 and V = 4
∴ V + F = E + 2
⇒ 4 + 4 = 6 + 2
⇒ 8 = 8
Hence, verified.
Question 16.
Complete the given table for prisms:
| Prism | Number Of faces | Number Of edges | Number Of vertices |
| Triangular | – | – | – |
| Quadrilateral | – | – | – |
| Pentagonal | – | – | – |
| Hexagonal | – | – | – |
| Octagonal | – | – | – |
| Decagonal | – | – | – |
Solution:
| Prism | Number Of faces | Number Of edges | Number Of vertices |
| Triangular | 5 | 9 | 6 |
| Quadrilateral | 6 | 12 | 8 |
| Pentagonal | 7 | 15 | 10 |
| Hexagonal | 8 | 18 | 12 |
| Octagonal | 10 | 24 | 16 |
| Decagonal | 12 | 30 | 20 |
Basic Geometrical Ideas Class 6 Extra Questions Multiple Choice Type
Question 17.
Number of right angles turned by the hour hand of a clock when it goes from 3 to 6.
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
Correct option is (a).
Question 18.
A quadrilateral having a pair of unequal opposite sides is called
(a) Parallelogram
(b) Square
(c) Rectangle
(d) Trapezium
Solution:
The correct option is (d).
Basic Geometrical Ideas Class 6 Extra Questions Higher Order Thinking Skills (Hots)
Question 19.
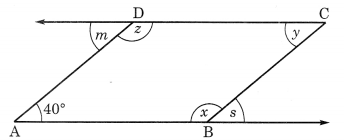
In the given figure, find the values of x, y, z, s and m.
Solution:
Given that ∠A = 40°
(i) ∠DAB + ∠ABC = 180° (adjacent angles)
⇒ 40° + ∠ABC = 180°
⇒ ∠ABC = 180° – 40° = 140°
Hence, ∠x = 140°
(ii) ∠x + ∠y = 180° (adjacent angles)
⇒ 140° + ∠y = 180°
⇒ ∠y = 180° – 140° = 40°
Hence, ∠y = 40°
(iii) ∠y + ∠z – 180° (adjacent angles)
⇒ 40° + ∠z = 180°
⇒ ∠z = 180° – 40° = 140°
Hence, ∠z = 140°
(iv) ∠x + ∠s = 180° (straight angles)
⇒ 140° + ∠s = 180°
⇒ ∠s = 180° – 140° = 40°
Hence, ∠s = 40°
(v) ∠m + ∠z = 180° (straight angles)
⇒ ∠m + 140° = 180°
⇒ ∠m = 180° – 140° = 40°
Question 20.
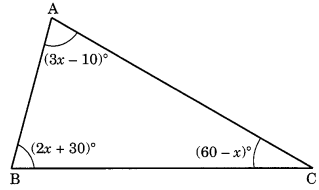
Find the value of x from the given figure and hence find the measure of each angle of the triangle.
Solution:
(i) Sum of the three angles of a triangle = 180°
∴ 2x + 30° + 60° – x + 3x – 10° = 180°
⇒ (2x – x + 3x) + (30° + 60° – 10°) = 180°
⇒ 4x + 80° = 180°
⇒ 4x = 180° – 80°
⇒ 4x = 100°
∴ x = \(\frac { { 100 }^{ 0 } }{ 4 }\) = 25°
∴ Measure of the angles are:
(i) (2x + 30)° – 2 x 25° + 30° = 80°
(ii) (60 – x)° = 60° – 25° = 35°
(iii) (3x – 10)° = 3 x 25° – 10° = 75° – 10° = 65°
Hence, x = 25° and the angles of the triangles are: 80°, 35° and 65°.