RD Sharma Class 9 solutions Chapter 25 Probability
RD Sharma Class 9 Solution Chapter 25 Probability Ex 25.1
Question 1.
A coin is tossed 1000 times with the following frequencies
Head : 455, Tail : 545.
Compute the probability for each event.
Solution:
Total number of events (m) 1000
(i) Possible events (m) 455
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 455 }{ 1000 } \)
= \(\frac { 91 }{ 200 } \) = 0.455
(ii) Possible events (m) = 545
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 545 }{ 1000 } \) = \(\frac { 109 }{ 200 } \) = 0.545
Question 2.
Two coins are tossed simultaneously 500 times with the following frequencies of different
outcomes:
Two heads : 95 times
One tail : 290 times
No head: 115 times
Find the probability of occurrence of each of these events.
Solution:
Two coins are tossed together simultaneously 500 times
∴ Total outcomes (n) 500
(i) 2 heads coming (m) = 95 times
∴Probability P(A) = \(\frac { m }{ n } \)
= \(\frac { No. of possible events }{ Total number of events } \)
= \(\frac { 95 }{ 500 } \) = \(\frac { 19 }{ 100 } \) = 0.19
(ii) One tail (m) = 290 times
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 290 }{ 500 } \) = \(\frac { 580 }{ 1000 } \) = \(\frac { 58 }{ 100 } \) = 0.58
(iii) No head (m) = 115 times
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 115 }{ 500 } \) = \(\frac { 23 }{ 100 } \) = 0.23
Question 3.
Three coins are tossed simultaneously 1oo times with the following frequencies of different outcomes:

If the three coins are simultaneously tossed again, compute the probability of:
(i) 2 heads coming up.
(ii) 3 heads coming up.
(iii) at least one head coming up.
(iv) getting more heads than tails.
(v) getting more tails than heads.
Solution:
Three coins are tossed simultaneously 100 times
Total out comes (n) = 100

(i) Probability of 2 heads coming up (m) = 36
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 36 }{ 100 } \) = 0.36
(ii) Probability of 3 heads (m) = 12
ProbabilityP(A)= \(\frac { m }{ n } \) = \(\frac { 12 }{ 100 } \) = 0.12
(iii) Probability of at least one head coming up (m) = 38 + 36 + 12 = 86
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 86 }{ 100 } \) = 0.86
(iv) Probability of getting more heads than tails (m) = 36 + 12 = 48
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 48 }{ 100 } \) = 0.48
(v) Getting more tails than heads (m) = 14 + 38 = 52
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 52 }{ 100 } \) = 0.52
Question 4.
1500 families with 2 children were selected randomly and the following data were recorded:

If a family is chosen at random, compute the probability that it has:
(i) No girl
(ii) 1 girl
(iii) 2 girls
(iv) at most one girl
(v) more girls than boys
Solution:
Total number of families (n) = 1500

(i) Probability of a family having no girls (m) = 211
∴Probability P(A)= \(\frac { m }{ n } \) = \(\frac { 211 }{ 1500 } \) = 0.1406
(ii) Probability of a family having one girl (in) = 814
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 814 }{ 1500 } \) = 0.5426
(iii) Probability of a family having 2 girls (m) = 475
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 475 }{ 1500 } \) = 0.3166
(iv) Probability of a family having at the most one girls
∴m = 814 + 211 = 1025
∴Probability P(A) =\(\frac { m }{ n } \) = \(\frac { 1025 }{ 1500 } \) = 0.6833
(v) Probability of a family having more girls than boys (m) = 475
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 475 }{ 1500 } \) = 0.3166
Question 5.
In a cricket match, a batsman hits a boundary 6 times out of 30 balls he plays. Find the probability that on a ball played:
(i) he hits boundary
(ii) he does not hit a boundary.
Solution:
Total balls played (n) 30
No. of boundaries = 6
(i) When the batsman hits the boundary = 6
∴m = 6
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 6 }{ 30 } \) = \(\frac { 1 }{ 5 } \) = 0.2
(ii) When the batsman does not hit the boundary (m) = 30 – 6 = 24
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 24 }{ 30 } \) = \(\frac { 4 }{ 5 } \) = 0.8
Question 6.
The percentage of marks obtained by a student in monthly unit tests are given below:

Find the probability that the student gets:
(i) more than 70% marks
(ii) less than 70% marks
(iii) a distinction.
Solution:
Percentage of marks obtain in

(i) Probability of getting more than 70% marks (m) = In unit test II, III, V = 3
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 3 }{ 5 } \) = 0.6
(ii) Getting less then 70% marks = units test I and IV
∴m = 2
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2 }{ 5 } \) = 0.4
(iii) Getting a distinction = In test V (76 of marks)
∴m = 1
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 1 }{ 5 } \) = 0.2
Question 7.
To know the opinion of the students about Mathematics, a survey of 200 students was conducted. The data is recorded in the following table:

Find the probability that a student chosen at random
(i) likes Mathematics
(ii) does not like it.
Solution:
Total number of students (n) = 200

(i) Probability of students who like mathematics (m) = 135
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 135 }{ 200 } \) = 0.675
(ii) Probability of students who dislike mathematics (m) = 65
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 65 }{ 200 } \) = 0.325
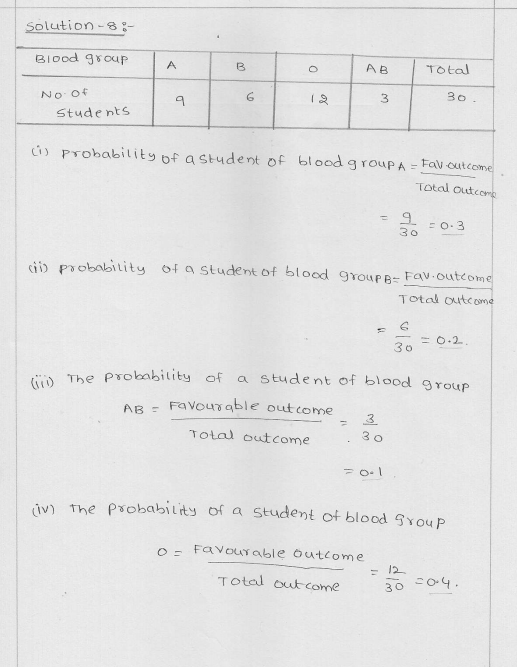
Question 8.
The blood groups of 30 students of class IX are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O,
A student is selected at random from the class from blood donation. Find the probability that the blood group of the student chosen is:
(i) A (ii) B (iii) AB (iv) O
Solution:
Total number of students of IX class = 30
No. of students of different blood groups
A AB B O
9 3 6 12

Question 9.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour
(in kg):
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Number of total bags (n) = 11
No. of bags having weight more than 5 kg (m) = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 11 } \)
Question 10.
Following table shows the birth month of 40 students of class IX.
![]()
Find the probability that a student was born in August.
Solution:
Total number of students (n) = 40
![]()
Number of students who born in Aug. (m) = 6
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 6 }{ 40 } \) = \(\frac { 3 }{ 20 } \)
Question 11.
Given below is the frequency distribution table regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days.

Find the probability of concentration of sulphur dioxide in the interval 0.12 – 0.16 on any of these days.
Solution:
Total number of days (n) = 30

Probability of cone, of S02 of the interval 0.12-0.16 (m) = 2
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2 }{ 30 } \) = \(\frac { 1 }{ 15 } \)
Question 12.
A company selected 2400 families at random and survey them to determine a relationship between income level and the number of vehicles in a home. The information gathered is listed in the table below:

If a family is chosen, find the probability that the family is:
(i)earning Rs 10000-13000 per month and owning exactly 2 vehicles.
(ii)earning Rs 16000 or more per month and owning exactly I vehicle.
(iii)earning less than Rs 7000 per month and does not own any vehicle.
(iv)earning Rs 13000-16000 per month and owning more than 2 vehicle.
(v)owning not more than 1 vehicle.
(vi)owning at least one vehicle.
Solution:
Total number of families (n) = 2400

(i) Number of families earning income Rs 10000-13000 and owning exactly 2 vehicles (m) = 29
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 29 }{ 2400 } \)
(ii) Number of families earning income Rs 16000 or more having one vehicle (m) = 579
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 579 }{ 2400 } \)
(iii) Number of families earning income less than Rs 7000 having no own vehicle (m) = 10
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 10 }{ 2400 } \) = \(\frac { 1 }{ 240 } \)
(iv) Number of families having X13000 to X16000 having more than two vehicles (m) = 25
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 25 }{ 2400 } \) = \(\frac { 1 }{ 96 } \)
(v) Number of families owning not more than one vehicle (m)
= 10 + 1 + 2 + 1 + 160 + 305 + 533 + 469 + 579 = 2062
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2062 }{ 2400 } \) = \(\frac { 1031 }{ 1200 } \)
(vi) Number of families owning at least one vechile (m) = 2048 + 192 + 110 = 2356
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2356 }{ 2400 } \) = \(\frac { 589 }{ 600 } \)
Question 13.
The following table gives the life time of 400 neon lamps:

A bulb is selected at random. Find the probability that the life time of the selected bulb is: (i) less than 400 (ii) between 300 to 800 hours (iii) at least 700 hours.
Solution:
Total number of neon lamps (n) = 400

A bulb is chosen:
(i)No. of bulbs having life time less than 400 hours (m) = 14
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 14 }{ 400 } \) = \(\frac { 7 }{ 200 } \)
(ii)No. of bulbs having life time between 300 to 800 hours (m) = 14 + 56 + 60 + 86 + 74 = 290
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 290 }{ 400 } \) = \(\frac { 29 }{ 40 } \)
(iii)No. of bulbs having life time at least 700 hours (m) = 74 + 62 + 48 = 184
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 184 }{ 400 } \) = \(\frac { 23 }{ 50 } \)
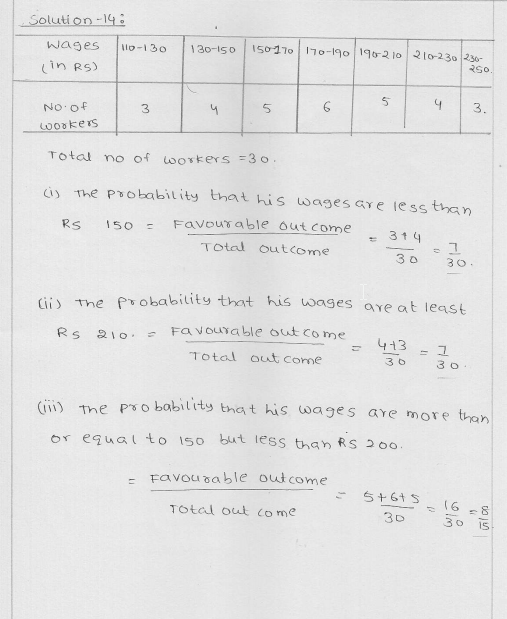
Question 14.
Given below is the frequency distribution of wages (in Rs) of 30 workers in a certain factory:

A worker is selected at random. Find the probability that his wages are:
(i) less than Rs 150
(ii) at least Rs 210
(iii) more than or equal to 150 but less than Rs 210.
Solution:
A worker is selected.
(i)No. of workers having less than Rs 150 (m) = 3 + 4 = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 30 } \)
(ii)No. of workers having at least Rs 210 (m) = 4 + 3 = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 30 } \)
(iii)No. of workers having more than or equal to Rs 150 but less than Rs 210 = 5 + 6 + 5 = 16
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 16 }{ 30 } \) = \(\frac { 8 }{ 15 } \)
Probability Class 9 RD Sharma Solutions VSAQS
Question 1.
Define a trial.
Solution:
When we perform an experiment, it is called a trial of the experiment.
Question 2.
Define an elementary event.
Solution:
An outcome of a trial of an experiment is called an elementary event.
Question 3.
Define an event.
Solution:
An event association to a random experiment is said to occur in a trial.
Question 4.
Define probability of an event.
Solution:
In n trials of a random experiment if an event A happens m times, then probability of happening
of A is given by P(A) = \(\frac { m }{ n } \)
Question 5.
A bag contains 4 white balls and some red balls. If the probability of drawing a white ball from the bag is \(\frac { 2 }{ 5 } \), find the number of red balls in the bag
Solution:
No. of white balls = 4
Let number of red balls = x
Then total number of balls (n) = 4 white + x red = (4 + x) balls

Question 6.
A die is thrown 100 times. If the probability of getting an even number is \(\frac { 2 }{ 5 } \). How many times an odd number is obtained?
Solution:
Total number of a die is thrown = 100
Let an even number comes x times, then probability of an even number = \(\frac { x }{ 100 } \)

Question 7.
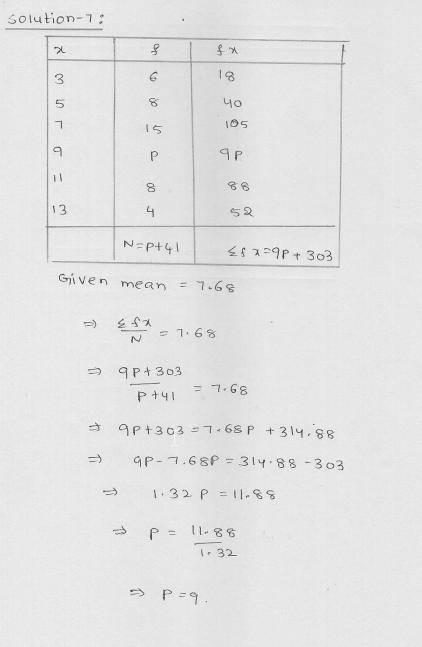
Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes

Find the probability of getting at most two heads.
Solution:
Total number of three coins are tossed (n) = 200
Getting at the most 2 heads (m) = 72 + 77 + 28 = 177
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 177 }{ 200 } \)
Question 8.
In the Q. No. 7, what is the probability of getting at least two heads?
Solution:
Total number of possible events = 200
No. of events getting at the least = 2 heads (m) = 23 + 72 = 95
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 95 }{ 200 } \) = \(\frac { 19 }{ 40 } \)
RD Sharma Class 9 PDF Chapter 25 Probability MCQS
Mark the correct alternative in each of the following:
Question 1.
The probability of an impossible event is
(a) 1
(b) 0
(c) less than 0
(d) greater than 1
Solution:
The probability of an impossible event is 0 (b)
Question 2.
The probability on a certain event is
(a) 0
(b) 1
(c) greater than 1
(d) less than 1
Solution:
The probability of a certain event is 1 (b)
Question 3.
The probability of an event of a trial is
(a) 1
(b) 0
(c) less than 1
(d) more than 1
Solution:
The probability of an even of a trial is less than 1 (c)
Question 4.
Which of the following cannot be the probability of an event?
(a) \(\frac { 1 }{ 3 } \)
(b) \(\frac { 3 }{ 5 } \)
(c) \(\frac { 5 }{ 3 } \)
(d) 1
Solution:
The probability of an event is less than 1
\(\frac { 5 }{ 3 } \) i.e .\(1\frac { 2 }{ 3 } \) is not the probability
Question 5.
Two coins are tossed simultaneously. The probability of getting atmost one head is
(a) \(\frac { 1 }{ 4 } \)
(b) \(\frac { 3 }{ 4 } \)
(c) \(\frac { 1 }{ 2 } \)
(d) \(\frac { 1 }{ 4 } \)
Solution:
Total number of possible events (n) = 2 + 2 = 4
Number of events coming at the most 1 head (m) 2 times + 1 times = 3
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 3 }{ 4 } \) (b)
Question 6.
A coin is tossed 1000 times, if the probability of getting a tail is 3/8, how many times head is obtained?
(a) 525
(b) 375
(c) 625
(d) 725
Solution:
No. of times a coin is tossed (n) = 1000
Probability of getting a tail = \(\frac { 3 }{ 8 } \)
Let No. of tail come = x
Probability P(A) = \(\frac { m }{ n } =\frac { x }{ 1000 } \)
\(\frac { x }{ 1000 } \) = \(\frac { 3 }{ 8 } \)
=> \(\frac { x }{ 1000 } =\frac { 3 }{ 8 } \) => \(\frac { 3X1000 }{ 8 } =3X125\)
=> x = 375
∴ No. of heads are obtained = 1000 – 375 = 625 (c)
Question 7.
A dice is rolled 600 times and the occurrence of the outcomes 1, 2, 3, 4, 5 and 6 are given below:

The probability of getting a prime number is
(a)\(\frac { 1 }{ 3 } \)
(b)\(\frac { 2 }{ 3 } \)
(c)\(\frac { 49 }{ 60 } \)
(d)\(\frac { 39 }{ 125 } \)
Solution:
Total number of times a dice is rolled (n) = 600

Now total number of times getting a prime number i.e. 2, 3, 5, (m) = 30 + 120 + 50 = 200
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 200 }{ 600 } \) = \(\frac { 1 }{ 3 } \) (a)
Question 8.
The percentage of attendance of different classes in a year in a school is given below:

What is the probability that the class attendance is more than 75%?
(a) \(\frac { 1 }{ 6 } \)
(b) \(\frac { 1 }{ 3 } \)
(c) \(\frac { 5 }{ 6 } \)
(d) \(\frac { 1 }{ 2 } \)
Solution:
Percentage of attendance of different classes

Total attendance more than 75% (m) VIII,VII and VI = 3 classes
and total number of classes (n) = 6
Probability P(A) = \(\frac { 3 }{ 6 } \) = \(\frac { 1 }{ 2 } \).
Question 9.
A bag contains 50 coins and each coin is marked from 51 to 100. One coin is picked at random.
The probability that the number on the coin is not a prime number, is
(a) \(\frac { 1 }{ 5 } \)
(b) \(\frac { 3 }{ 5 } \)
(c) \(\frac { 2 }{ 5 } \)
(d) \(\frac { 4 }{ 5 } \)
Solution:
Total number of coins (n) = 50
Prime numbers between 51 to 100 are 53, 59, 6, 67, 71, 73, 79, 83, 89, 97 = 10
Numbers which are not primes (m) = 50 – 10 = 40
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 40 }{ 50 } \) = \(\frac { 4 }{ 5 } \)(d)
Question 10.
In a football match, Ronaldo makes 4 pals from 10 penalty kids. The probability of converting a penalty kick into a goal by Ronaldo,is
(a) \(\frac { 1 }{ 4 } \)
(b) \(\frac { 1 }{ 6 } \)
(c) \(\frac { 1 }{ 3 } \)
(d) \(\frac { 2 }{ 5 } \)
Solution:
No. of penalty kicks (n) = 10
No. of goal scored (m) = 4
Probability of converting a penally Into goals P(A) = \(\frac { 4 }{ 10 } \) = \(\frac { 2 }{ 5 } \)(d)
RD Sharma Class 9 solutions Chapter 25 Probability









NCERT Solutions for maths in Video
https://www.youtube.com/user/cbsepapers/videos
CBSE sample papers
http://www.cbsesamplepapers.info/
RD Sharma Class 9 Solutions