RD Sharma class 10 solutions Chapter 8 Quadratic Equations Ex 8.12
RD
Question 1.
A takes 10 days less than the time taken by B to finish a piece of work. If both A and B together can finish the work in 12 days, find the time taken by B to finish the work. .
Solution:
Let B can do the work in = x days
A will do the same work in = (x – 10) days
A and B both can finish the work in = 12 days
According to the condition,

⇒ x (x – 4) – 30 (x – 4) = 0
⇒ (x – 4) (x – 30) = 0
Either x – 4 = 0, then x = 4
or x – 30 = 0, then x = 30
But x = 4 is not possible
B can finish the work in 30 days
Question 2.
If two pipes function simultaneously, a reservoir will be filled in 12 hours. One pipe fills the reservoir 10 hours faster than the other. How many hours will the second pipe take to fill the reservoir ?
Solution:
Two pipes can fill the .reservoir in = 12 hours
Let first pipe can fill the reservoir in = x hrs
Then second pipe will fill it in = (x – 10) hours
Now according to the condition,

⇒ x² – 10x = 24x – 120
⇒ x² – 10x – 24x + 120 = 0
⇒ x² – 34x + 120 = 0
⇒ x² – 30x – 4x + 120 = 0
⇒ x (x – 30) – 4 (x – 30) = 0
⇒ (x – 30) (x – 4) = 0
Either x – 30 = 0, then x = 30
or x – 4 = 0 but it is not possible as it is < 10
The second pipe will fill the reservoir in = x – 10 = 30 – 10 = 20 hours
Question 3.
Two water taps together can fill a tank in 9\(\frac { 3 }{ 8 }\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Two taps can fill the tank in = 9\(\frac { 3 }{ 8 }\) = \(\frac { 75 }{ 8 }\) hr
Let smaller tap fill the tank in = x hours
Then larger tap will fill it in = (x – 10) hours
According to the condition,


Smaller tap can fill the tank in = 25 hours
and larger tap can fill the tank in = 25 – 10 = 15 hours
Question 4.
Tw o pipes running together can fill a tank in 11\(\frac { 1 }{ 9 }\) minutes. If one pipe takes 5 minutes more than the other to fill the tank separately, find the time in which each pipe would fill the tank separately. [CBSE 2010]
Solution:RD Sharma Class 10 Solutions Chapter 8 Quadratic Equations
” width=”374″ height=”454″ />
⇒ 9x (x – 20) + 25 (x – 20) = 0
⇒ (x – 20) (9x + 25) = 0
Either x = – 20 = 0, then x = 20 or 9x + 25 = 0 then 9x = -25
⇒ x = \(\frac { -25 }{ 9 }\) but it is not possible being negative
x = 20
Time taken by the two pipes = 20 minutes and 20 + 5 = 25 minutes
Question 5.
To fill a swimming pool two pipes are used. If the pipe of larger diameter used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool? [CBSE 2015]
Solution:
Let pipe of larger diameter can fill the tank = x hrs
and pipe of smaller diameter can fill in = y hrs

⇒ 26x + 80 = x² + 10x
⇒ x² + 10x – 26x – 80 = 0
⇒ x² – 16x – 80 = 0
⇒ x² – 20x + 4x – 80 = 0
⇒ x (x – 20) + 4 (x – 20) = 0
⇒ (x – 20) (x + 4) = 0
Either x – 20 = 0, then x = 20
or x + 4 = 0, then x = – 4 which is not possible
x = 20 and y = 10 + x = 10 + 20 = 30
Larger pipe can fill the tank in 20 hours and smaller pipe can fill in 30 hours.
Sharma

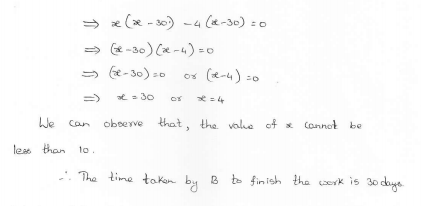


RD Sharma Class 10 Solutions
- Chapter 8 Quadratic Equations Ex 8.1
- Chapter 8 Quadratic Equations Ex 8.2
- Chapter 8 Quadratic Equations Ex 8.3
- Chapter 8 Quadratic Equations Ex 8.4
- Chapter 8 Quadratic Equations Ex 8.5
- Chapter 8 Quadratic Equations Ex 8.6
- Chapter 8 Quadratic Equations Ex 8.7
- Chapter 8 Quadratic Equations Ex 8.8
- Chapter 8 Quadratic Equations Ex 8.9
- Chapter 8 Quadratic Equations Ex 8.10
- Chapter 8 Quadratic Equations Ex 8.11
- Chapter 8 Quadratic Equations Ex 8.12
- Chapter 8 Quadratic Equations Ex 8.13