CBSE Class 11 Maths Notes Chapter 7 Permutations and Combinations
Fundamental Principles of Counting
Multiplication Principle: Suppose an operation A can be performed in m ways and associated with each way of performing of A, another operation B can be performed in n ways, then total number of performance of two operations in the given order is mxn ways. This can be extended to any finite number of operations.
Addition Principle: If an operation A can be performed in m ways and another operation S, which is independent of A, can be performed in n ways, then A and B can performed in (m + n) ways. This can be extended to any finite number of exclusive events.
Factorial
The continued product of first n natural number is called factorial ‘n’.
It is denoted by n! or n! = n(n – 1)(n – 2)… 3 × 2 × 1 and 0! = 1! = 1
Permutation
Each of the different arrangement which can be made by taking some or all of a number of objects is called permutation.
Permutation of n different objects
The number of arranging of n objects taking all at a time, denoted by
n
P
n
, is given by
n
P
n
= n!
The number of an arrangement of n objects taken r at a time, where 0 < r ≤ n, denoted by nP
r
is given by
n
P
r
= \(\frac { n! }{ \left( n-r \right) ! }\)
Properties of Permutation
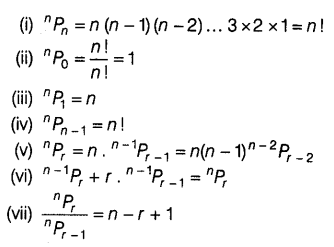
Important Results on Permutation
The number of permutation of n things taken r at a time, when repetition of object is allowed is nr.
The number of permutation of n objects of which p1 are of one kind, p2 are of second kind,… pk are of kth kind such that p 1 + p 2 + p 3 + … + p k = n is \(\frac { n! }{ { { p }_{ 1 }!{ { p }_{ 2 }!{ p }_{ 3 }!…..{ p }_{ k }! } } }\)
Number of permutation of n different objects taken r at a time,
When a particular object is to be included in each arrangement is r.
n-1
P
r-1
When a particular object is always excluded, then number of arrangements = n-1 P r .
Number of permutations of n different objects taken all at a time when m specified objects always come together is m! (n – m + 1)!.
Number of permutation of n different objects taken all at a time when m specified objects never come together is n! – m! (n – m + 1)!.
Combinations
Each of the different selections made by taking some or all of a number of objects irrespective of their arrangements is called combinations. The number of selection of r objects from; the given n objects is denoted by
n
C
r
, and is given by
n
C
r
= \(\frac { n! }{ r!\left( n-r \right) ! }\)
Properties of Combinations
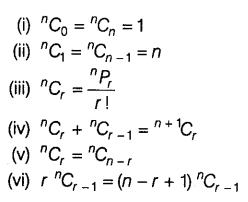
CBSE Class 11 Maths Notes Chapterwise
- Chapter 1 Sets Class 11 Notes
- Chapter 2 Relations and Functions Class 11 Notes
- Chapter 3 Trigonometric Functions Class 11 Notes
- Chapter 4 Principle of Mathematical Induction Class 11 Notes
- Chapter 5 Complex Numbers and Quadratic Equations Class 11 Notes
- Chapter 6 Linear Inequalities Class 11 Notes
- Chapter 7 Permutations and Combinations Class 11 Notes
- Chapter 8 Binomial Theorem Class 11 Notes
- Chapter 9 Sequences and Series Class 11 Notes
- Chapter 10 Straight Lines Class 11 Notes
- Chapter 11 Conic Sections Class 11 Notes
- Chapter 12 Introduction to Three Dimensional Geometry Class 11 Notes
- Chapter 13 Limits and Derivatives Class 11 Notes
- Chapter 14 Mathematical Reasoning Class 11 Notes
- Chapter 15 Statistics Class 11 Notes
- Chapter 16 Probability Class 11 Notes