NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.2

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Ex 14.2

• Class 8 Maths Factorisation Exercise 14.1
• Class 8 Maths Factorisation Exercise 14.2
• Class 8 Maths Factorisation Exercise 14.3
• Factorisation Class 8 Extra Questions

NCERT Solutions for Class 8 Maths Chapter 14 Factorisation Exercise 14.2

Ex 14.2 Class 8 Maths Question 1.
Factorise the following expressions.
(i) a ² + 8a +16
(ii) p ² – 10p + 25
(iii) 25m ² + 30m + 9
(iv) 49y ² + 84yz + 36z ²
(v) 4x ² – 8x + 4
(vi) 121b ² – 88bc + 16c ²
(vii) (l + m) ² – 4lm. (Hint: Expand (l + m) ² first)
(viii) a ⁴ + 2a ² b ² + b ⁴
Solution:
(i) a ² + 8a + 16
Here, 4 + 4 = 8 and 4 × 4 = 16
a ² + 8a +16
= a ² + 4a + 4a + 4 × 4
= (a ² + 4a) + (4a + 16)
= a(a + 4) + 4(a + 4)
= (a + 4) (a + 4)
= (a + 4) ²

(ii) p ² – 10p + 25
Here, 5 + 5 = 10 and 5 × 5 = 25
p ² – 10p + 25
= p ² – 5p – 5p + 5 × 5
= (p ² – 5p) + (-5p + 25)
= p(p – 5) – 5(p – 5)
= (p – 5) (p – 5)
= (p – 5) ²

(iii) 25m ² + 30m + 9
Here, 15 + 15 = 30 and 15 × 15 = 25 × 9 = 225
25m ² + 30m + 9
= 25m ² + 15m + 15m + 9
= (25m ² + 15m) + (15m + 9)
= 5m(5m + 3) + 3(5m + 3)
= (5m + 3) (5m + 3)
= (5m + 3) ²

(iv) 49y ² + 84yz + 36z ²
Here, 42 + 42 = 84 and 42 × 42 = 49 × 36 = 1764
49y ² + 84yz + 36z ²
= 49y ² + 42yz + 42yz + 36z ²
= 7y(7y + 6z) +6z(7y + 6z)
= (7y + 6z) (7y + 6z)
= (7y + 6z) ²

(v) 4x ² – 8x + 4
= 4(x ² – 2x + 1) [Taking 4 common]
= 4(x ² – x – x + 1)
= 4[x(x – 1) -1(x – 1)]
= 4(x – 1)(x – 1)
= 4(x – 1) ²

(vi) 121b ² – 88bc + 16c ²
Here, 44 + 44 = 88 and 44 × 44 = 121 × 16 = 1936
121b ² – 88bc + 16c ²
= 121b ² – 44bc – 44bc + 16c ²
= 11b(11b – 4c) – 4c(11b – 4c)
= (11b – 4c) (11b – 4c)
= (11b – 4c) ²

(vii) (l + m) ² – 4lm
Expanding (l + m) ² , we get
l ² + 2lm + m ² – 4lm
= l ² – 2lm + m ²
= l ² – Im – lm + m ²
= l(l – m) – m(l – m)
= (l – m) (l – m)
= (l – m) ²

(viii) a ⁴ + 2a ² b ² + b ⁴
= a ⁴ + a ² b ² + a ² b ² + b ⁴
= a ² (a ² + b ² ) + b ² (a ² + b ² )
= (a ² + b ² )(a ² + b ² )
= (a ² + b ² ) ²

Ex 14.2 Class 8 Maths Question 2.
Factorise.
(i) 4p ² – 9q ²
(ii) 63a ² – 112b ²
(iii) 49x ² – 36
(iv) 16x ⁵ – 144x ³
(v) (l + m) ² – (l – m) ²
(vi) 9x ² y ² – 16
(vii) (x ² – 2xy + y ² ) – z ²
(viii) 25a ² – 4b ² + 28bc – 49c ²
Solution:
(i) 4p ² – 9q ²
= (2p) ² – (3q) ²
= (2p – 3q) (2p + 3q)
[∵ a ² – b ² = (a + b)(a – b)]

(ii) 63a ² – 112b ²
= 7(9a ² – 16b ² )
= 7 [(3a) ² – (4b) ² ]
= 7(3a – 4b)(3a + 4b)
[∵ a ² – b ² = (a + b)(a – b)]

(iii) 49x ² – 36 = (7x) ² – (6) ²
= (7x – 6) (7x + 6)
[∵ a ² – b ² = (a + b)(a – b)]

(iv) 16x ⁵ – 144x ³ = 16x ³ (x ² – 9)
= 16x ³ [(x) ² – (3) ² ]
= 16x ³ (x – 3)(x + 3)
[∵ a ² – b ² = (a + b)(a – b)]

(v) (l + m) ² – (l – m) ²
= (l + m) – (l – m)] [(l + m) + (l – m)]
[∵ a ² – b ² = (a + b)(a – b)]
= (l + m – l + m)(l + m + l – m)
= (2m) (2l)
= 4ml

(vi) 9x ² y ² – 16 = (3xy) ² – (4) ²
= (3xy – 4)(3xy + 4)
[∵ a ² – b ² = (a + b)(a – b)]

(vii) (x ² – 2xy + y ² ) – z ²
= (x – y) ² – z ²
= (x – y – z) (x – y + z)
[∵ a ² – b ² = (a + b)(a – b)]

(viii) 25a ² – 4b ² + 28bc – 49c ²
= 25a ² – (4b ² – 28bc + 49c ² )
= (5a) ² – (2b – 7c) ²
= [5a – (2b – 7c)] [5a + (2b – 7c)]
= (5a – 2b + 7c)(5a + 2b – 7c)

Ex 14.2 Class 8 Maths Question 3.
Factorise the expressions.
(i) ax ² + bx
(ii) 7p ² + 21q ²
(iii) 2x ³ + 2xy ² + 2xz ²
(iv) am ² + bm ² + bn ² + an ²
(v) (lm + l) + m + 1
(vi) y(y + z) + 9(y + z)
(vii) 5y ² – 20y – 8z + 2yz
(viii) 10ab + 4a + 5b + 2
(ix) 6xy – 4y + 6 – 9x
Solution:
(i) ax ² + bx = x(ax + 5)

(ii) 7p ² + 21q ² = 7(p ² + 3q ² )

(iii) 2x ³ + 2xy ² + 2xz ² = 2x(x ² + y ² + z ² )

(iv) am ² + bm ² + bn ² + an ²
= m ² (a + b) + n ² (a + b)
= (a + b)(m ² + n ² )

(v) (lm + l) + m + 1
= l(m + 1) + (m + 1)
= (m + 1) (l + 1)

(vi) y(y + z) + 9(y + z) = (y + z)(y + 9)

(vii) 5y ² – 20y – 8z + 2yz
= 5y ² – 20y + 2yz – 8z
= 5y(y – 4) + 2z(y – 4)
= (y – 4) (5y + 2z)

(viii) 10ab + 4a + 5b + 2
= 2a(5b + 2) + 1(5b + 2)
= (5b + 2)(2a + 1)

(ix) 6xy – 4y + 6 – 9x
= 6xy – 4y – 9x + 6
= 2y(3x – 2) – 3(3x – 2)
= (3x – 2) (2y – 3)

Ex 14.2 Class 8 Maths Question 4.
Factorise.
(i) a ⁴ – b ⁴
(ii) p ⁴ – 81
(iii) x ⁴ – (y + z) ⁴
(iv) x ⁴ – (x – z) ⁴
(v) a ⁴ – 2a ² b ² + b ⁴
Solution:
(i) a ⁴ – b ⁴ – (a ² ) ² – (b ² ) ²
[∵ a ² – b ² = (a – b)(a + b)]
= (a ² – b ² ) (a ² + b ² )
= (a – b) (a + b) (a ² + b ² )

(ii) p ⁴ – 81 = (p ² ) ² – (9) ²
= (p ² – 9) (p ² + 9)
[∵ a ² – b ² = (a – b)(a + b)]
= (p – 3)(p + 3) (p ² + 9)

(iii) x ⁴ – (y + z) ⁴ = (x ² ) ² – [(y + z) ² ] ²
[∵ a ² – b ² = (a – b)(a + b)]
= [x ² – (y + z) ² ] [x ² + (y + z) ² ]
= [x – (y + z)] [x + (y + z)] [x ² + (y + z) ² ]
= (x – y – z) (x + y + z) [x ² + (y + z) ² ]

(iv) x ⁴ – (x – z) ⁴ = (x ² ) ² – [(y – z) ² ] ²
= [x ² – (y – z) ² ] [x ² + (y – z) ² ]
= (x – y + z) (x + y – z) (x ² + (y – z) ² ]

(v) a ⁴ – 2a ² b ² + b ⁴
= a ⁴ – a ² b ² – a ² b ² + b ⁴
= a ² (a ² – b ² ) – b ² (a ² – b ² )
= (a ² – b ² )(a ² – b ² )
= (a ² – b ² ) ²
= [(a – b) (a + b)] ²
= (a – b) ² (a + b) ²

Ex 14.2 Class 8 Maths Question 5.
Factorise the following expressions.
(i) p ² + 6p + 8
(ii) q ² – 10q + 21
(iii) p ² + 6p – 16
Solution:
(i) p ² + 6p + 8
Here, 2 + 4 = 6 and 2 × 4 = 8
p ² + 6p + 8
= p ² + 2p + 4p + 8
= p (p + 2) + 4(p + 2)
= (p + 2) (p + 4)

(ii) q ² – 10q + 21
Here, 3 + 7 = 10 and 3 × 7 = 21
q ² – 10q + 21
= q ² – 3q – 7q + 21
= q(q – 3) – 7(q – 3)
= (q – 3) (q – 7)

(iii) p ² + 6p – 16
Here, 8 – 2 = 6 and 8 × 2 = 16
p ² + 6p – 16
= p ² + 8p – 2p – 16
= p(p + 8) – 2(p + 8)
= (p + 8) (p – 2)

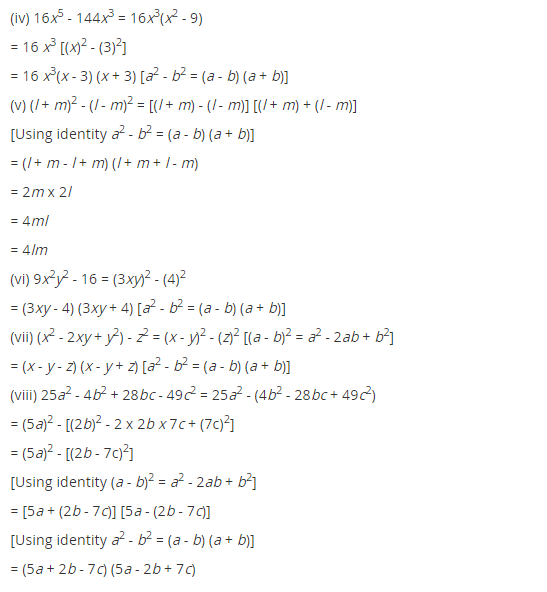
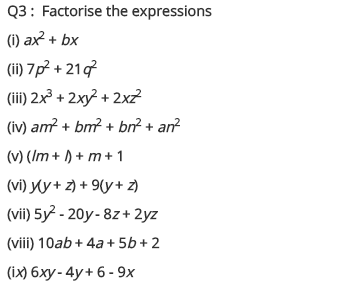
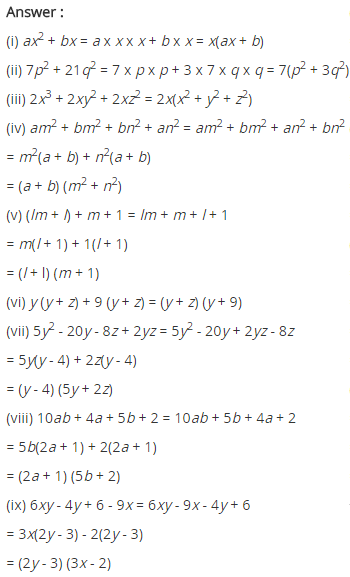
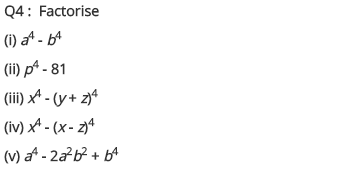
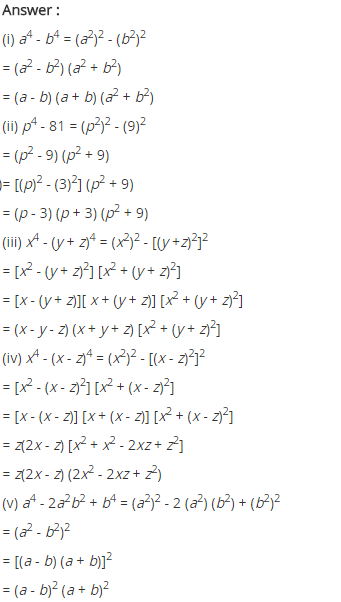
More CBSE Class 8 Study Material

• NCERT Solutions for Class 8 Maths
• NCERT Solutions for Class 8 Science
• NCERT Solutions for Class 8 Social Science
• NCERT Solutions for Class 8 English
• NCERT Solutions for Class 8 English Honeydew
• NCERT Solutions for Class 8 English It So Happened
• NCERT Solutions for Class 8 Hindi
• NCERT Solutions for Class 8 Sanskrit
• NCERT Solutions