NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Ex 8.3
- Class 7 Maths Comparing Quantities Exercise 8.1
- Class 7 Maths Comparing Quantities Exercise 8.2
- Class 7 Maths Comparing Quantities Exercise 8.3
NCERT Solutions for Class 7 Maths Chapter 8 Comparing Quantities Exercise 8.3
Ex 8.3 Class 7 Maths Question 1.
Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for ₹ 250 and sold for ₹ 325.
(b) A refrigerator bought for ₹ 12,000 and sold at ₹ 13,500.
(c) A cupboard bought for ₹ 2,500 and sold at ₹ 3,000.
(d) A skirt bought for ₹ 250 and sold at ₹ 150.
Solution:
(a) Here, CP = ₹ 250
SP = ₹ 325
Since SP > CP
∴ Profit = SP – CP
= ₹ 325 – ₹ 250 = ₹ 75
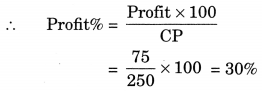
Hence, the required profit = ₹ 75
and Profit per cent = 30%
(b) Here, CP = ₹ 12,000
SP = ₹ 13,500
Since SP > CP
∴ Profit = SP – CP
= ₹ 13,500 – ₹ 12,000 = ₹ 1,500
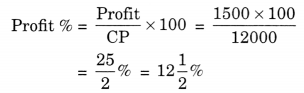
Hence, the required profit = ₹ 1500 × 100
profit % = \(12 \frac{1}{2}\)%
(c) Here, CP = ₹ 2500
SP = ₹ 3000
Since SP > CP
∴ Profit = SP – CP
= ₹ 3000 – ₹ 2500 = ₹ 500

Hence, the required profit = ₹ 500 and profit% = 20%
(d) Here, CP = ₹ 250
SP = ₹ 150
Here CP > SP
∴ Loss = CP – SP
= ₹ 250 – ₹ 150 = ₹ 100
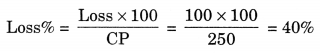
Hence, the required loss = ₹ 100 and loss% = 40%
Ex 8.3 Class 7 Maths Question 2.
Convert each part of the ratio to Percentage:
(a) 3:1
(b) 2:3:5
(c) 1 : 4
(d) 1:2:5
Solution:
(a) 3 : 1
Sum of the ratio parts = 3 + 1 = 4
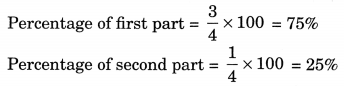
(b) 2 : 3 : 5
Sum of the ratio parts = 2 + 3 + 5 = 10

(c) 1 : 4
Sum of the ratio parts =1 + 4 = 5
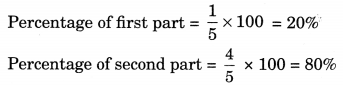
(d) 1 : 2 : 5
Sum of the ratio parts = 1 + 2 + 5 = 8

Ex 8.3 Class 7 Maths Question 3.
The population of a city decreased from 25,000 to 24,500. Find the Percentage decrease.
Solution:
Initial population = 25,000
Decreased population = 24,500
Decrease in population
= 25,000 – 24,500 = 500
Percentage of decrease = \(\frac{500 \times 100}{25000}\) = 2%
Hence the Percentage of decrease in population = 2%.
Ex 8.3 Class 7 Maths Question 4.
Arun bought a car for ₹ 3,50,000. The next year, the price went upto ₹ 3,70,000. What was the Percentage of price increase?
Solution:
Original price of the car = ₹ 3,50,000
Price increased next year = ₹ 3,70,000
Increase in price = ₹ 3,70,000 – ₹ 3,50,000
= ₹ 20,000
∴ Percentage of the increase in the price
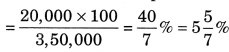
Hence, the Percentage of increase in price = \(5 \frac{5}{7} \%\)
Ex 8.3 Class 7 Maths Question 5.
I buy a TV for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?
Solution:
Here, CP = ₹ 10,000
Profit = 20%
SP = ?
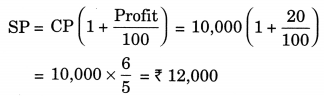
Hence, the required money got by me = ₹ 12,000.
Ex 8.3 Class 7 Maths Question 6.
Juhi sells a washing machine for ₹ 13,500. She loses 20% in the bargain. What was the price at which she bought it?
Solution:
SP of the washing machine = ₹ 13,500
Loss = 20%
CP = ?

Hence, the cost price of the machine = ₹ 16875.
Ex 8.3 Class 7 Maths Question 7.
(i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12. Find the Percentage of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3 g, what is the weight of the chalk stick?
Solution:
(i) Sum of the ratio parts = 10 + 3 + 12 = 25
∴ Percentage of carbon in chalk
= \(=\frac{3}{25} \times 100 \%=12 \%\)
Hence, the Percentage of carbon in chalk = 12%
(ii) Weight of carbon = 3 g
∴ Weight of chalk = \(=\frac{3}{3}\) × 25 g = 25 g
Hence, the weight of chalk = 25 g
Ex 8.3 Class 7 Maths Question 8.
Amina buys a book for ₹ 275 and sells it at a loss of 15%. How much does she sell it for?
Solution:
CP of book = ₹ 275
Loss = 15%
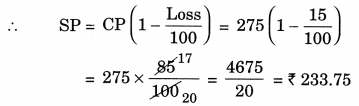
Hence, the required selling price = ₹ 233.75
Ex 8.3 Class 7 Maths Question 9.
Find the amount to be paid at the end of 3 years in each case.
(a) Principal = ₹ 1200 at 12% p.a.
(b) Principal = ₹ 7500 at 5% p.a.
Solution:
(a) Given: Principal = ₹ 1200
Rate of interest = 12% p.a., T = 3 years
∴ Interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}=\frac{1200 \times 12 \times 3}{100}\)
Amount = Principal + Interest
= ₹ 1200 + ₹ 432 = ₹ 1632
Hence, the required amount = ₹ 1632
(b) Given: Principal = ₹ 7500
Rate = 5% p.a.
Time = 3 years
∴ Interest = \(\frac{\mathrm{P} \times \mathrm{R} \times \mathrm{T}}{100}=\frac{7500 \times 5 \times 3}{100}\)
= ₹1125
Amount = Principal + Interest
= ₹ 7500 + 11125 = ₹ 8625
Hence, the required amount = ₹ 8625.
Ex 8.3 Class 7 Maths Question 10.
What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 years?
Solution:
Given: Principal = ₹ 56,000
Interest = ₹280
Time = 2 years
Rate = ?
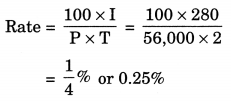
Hence, the required rate = 0.25%
Ex 8.3 Class 7 Maths Question 11.
If Meena gives an interest of ₹ 45 for one year at 9% rate p.a. What is the sum she has borrowed?
Solution:
Given: Interest = ₹ 45
Time = 1 year
Rate = 9% p.a.
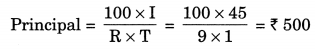
Hence, the required sum = ₹ 500.






NCERT Solutions Maths Science Social English Sanskrit Hindi RD Sharma