NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Ex 6.3
- Class 7 Maths The Triangle and Its Properties Exercise 6.1
- Class 7 Maths The Triangle and Its Properties Exercise 6.2
- Class 7 Maths The Triangle and Its Properties Exercise 6.3
- Class 7 Maths The Triangle and Its Properties Exercise 6.4
- Class 7 Maths The Triangle and Its Properties Exercise 6.5
NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties Exercise 6.3
Ex 6.3 Class 7 Maths Question 1.
Find the value of the unknown x in the following diagrams:
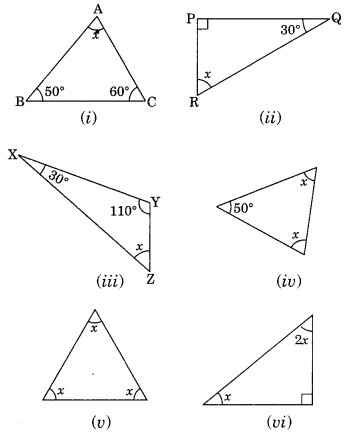
Solution:
(i) By angle sum property of a triangle, we have
∠x + 50° + 60° = 180°
⇒ ∠x + 110° = 180°
∴ ∠x = 180° – 110° = 70°
(ii) By angle sum property of a triangle, we have
∠x + 90° + 30 = 180° [∆ is right angled triangle]
⇒ ∠x + 120° = 180°
∴ ∠x – 180° – 120° = 60°
(iii) By angle sum property of a triangle, we have
∠x + 30° + 110° – 180°
⇒ ∠x + 140° = 180°
∴ ∠x = 180° – 140° = 40°
(iv ) By angle sum property of a triangle, we have
∠x + ∠x + 50° = 180°
⇒ 2x + 50° = 180°
⇒ 2x = 180° – 50°
⇒ 2x = 130°
∴ \(x=\frac{130^{0}}{2}=65^{\circ}\)
(v) By angle sum property of a triangle, we have
∠x + ∠x +∠x =180°
⇒ 3 ∠x = 180°
∴ \(\angle x=\frac{180^{0}}{3}=60^{\circ}\)
(vi) By angle sum property of a triangle, we have
x + 2 x + 90° = 180° (∆ is right angled triangle)
⇒ 3x + 90° = 180°
⇒ 3x = 180° – 90°
⇒ 3x = 90°
∴ \(x=\frac{90^{0}}{3}=30^{\circ}\)
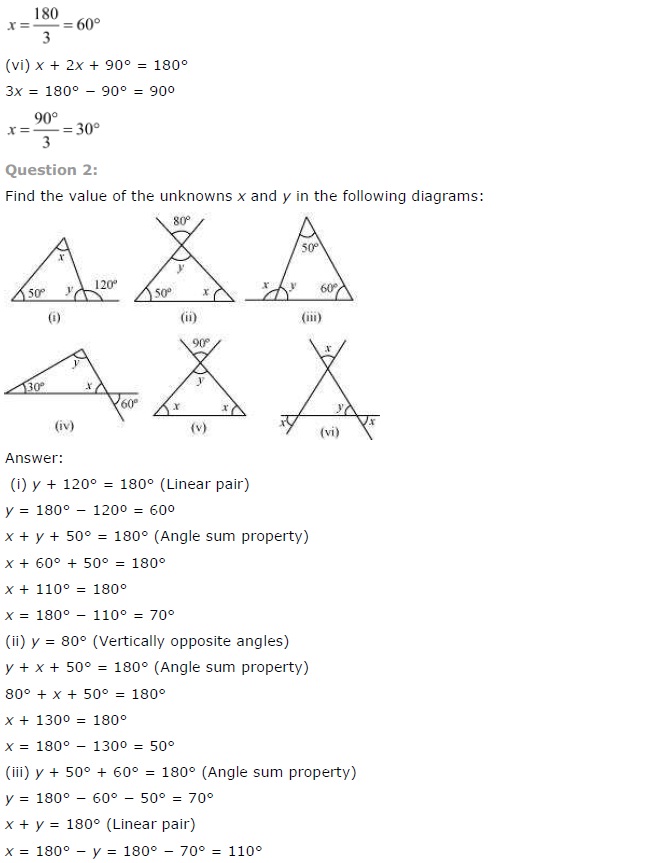
Ex 6.3 Class 7 Maths Question 2.
Find the values of the unknowns x and y in the following diagrams:
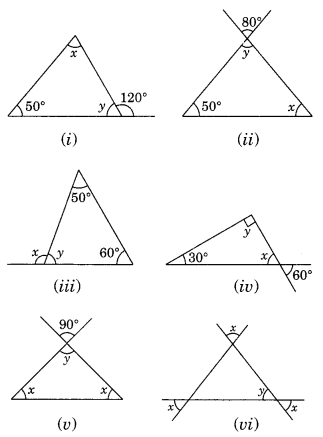
Solution:
(i) ∠x + 50° = 120° (Exterior angle of a triangle)
∴ ∠x = 120°- 50° = 70°
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
70° + ∠y + 50° = 180°
∠y + 120° = 180°
∠y = 180° – 120°
∴ ∠y = 60°
Thus ∠x = 70 and ∠y – 60°
(ii) ∠y = 80° (Vertically opposite angles are same)
∠x + ∠y + 50° = 180° (Angle sum property of a triangle)
⇒ ∠x + 80° + 50° = 180°
⇒ ∠x + 130° = 180°
∴ ∠x = 180° – 130° = 50°
Thus, ∠x = 50° and ∠y = 80°
(iii) ∠y + 50° + 60° = 180° (Angle sum property of a triangle)
∠y + 110° = 180°
∴ ∠y = 180°- 110° = 70°
∠x + ∠y = 180° (Linear pairs)
⇒ ∠x + 70° = 180°
∴ ∠x = 180° – 70° = 110°
Thus, ∠x = 110° and y = 70°
(iv) ∠x = 60° (Vertically opposite angles)
∠x + ∠y + 30° = 180° (Angle sum property of a triangle)
⇒ 60° + ∠y + 30° = 180°
⇒ ∠y + 90° = 180°
⇒ ∠y = 180° – 90° = 90°
Thus, ∠x = 60° and ∠y = 90°
(v) ∠y = 90° (Vertically opposite angles)
∠x + ∠x + ∠y = 180° (Angle sum property of a triangle)
⇒ 2 ∠x + 90° = 180°
⇒ 2∠x = 180° – 90°
⇒ 2∠x = 90°
∴ \(\angle x=\frac{90^{\circ}}{2}=45^{\circ}\)
Thus, ∠x = 45° and ∠y = 90°
(vi) From the given figure, we have
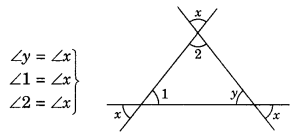
Adding both sides, we have
∠y + ∠1 + ∠2 = 3∠x
⇒ 180° = 3∠x (Angle sum property of a triangle)
∴ \(\angle x=\frac{180^{\circ}}{3}=60^{\circ}\)
∠x = 60°, ∠y = 60°

NCERT Solutions Maths Science Social English Sanskrit Hindi RD Sharma