NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Ex 11.3
- Class 7 Maths Perimeter and Area Exercise 11.1
- Class 7 Maths Perimeter and Area Exercise 11.2
- Class 7 Maths Perimeter and Area Exercise 11.3
- Class 7 Maths Perimeter and Area Exercise 11.4
NCERT Solutions for Class 7 Maths Chapter 11 Perimeter and Area Exercise 11.3
Ex 11.3 Class 7 Maths Question 1.
Find the circumference of the circles with the following radius. (Take π =\(\frac{22}{7}\))
(a) 14 cm
(b) 28 mm
(c) 21 cm
Solution:
(a) Given: Radius (r) = 14 cm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 14
= 88 cm
(b) Given: Radius (r) = 28 mm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 28
= 176 mm
(c) Given: Radius (r) = 21 cm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 21
= 132 cm
Ex 11.3 Class 7 Maths Question 2.
Find the area of the following circles, given that (Take π =\(\frac{22}{7}\))
(a) radius = 14 mm
(b) diameter = 49 m
(c) radius = 5 cm
Solution:
(a) Here, r = 14 mm
∴ Area of the circle = πr
2
= π × 14 × 14 = \(\frac{22}{7}\) × 14 × 14
(b) Here, diameter = 49 m 49
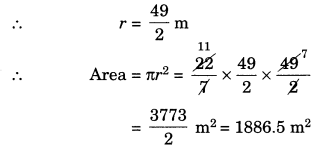
(c) Here, radius = 5 cm
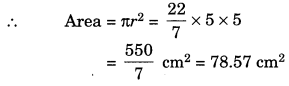
Ex 11.3 Class 7 Maths Question 3.
If the circumference of a circular sheet is 154 m, find its radius. Also find the area of the sheet. (Take π =\(\frac{22}{7}\))
Solution:
Given: Circumference = 154 m
∴ 2πr = 154
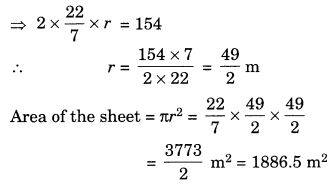
Ex 11.3 Class 7 Maths Question 4.
A gardener wants to fence a circular garden of diameter 21 m. Find the length of the rope he needs to purchase, if he makes 2 rounds offence. Also find the cost of the rope, if it costs ₹ 4 per metre. (Take π =\(\frac{22}{7}\))
Solution:
Diameter of the circular garden = 21 m
∴ Radius = \(\frac{21}{2}\) m
∴ Circumference = 2πr = \(2 \times \frac{22}{7} \times \frac{21}{2}\)
= 66 m
Length of rope needed for 2 rounds
= 2 × 66 m = 132 m
Cost of the rope = ₹4 × 132 = ₹ 528
Ex 11.3 Class 7 Maths Question 5.
From a circular sheet of radius 4 cm, a circle of radius 3 cm is removed. Find the area of the remaining sheet. (Take π = 3.14)
Solution:
Radius of the circular sheet = 4 cm
∴ Area = πr
2
= π × 4 × 4 = 16π cm
2
Radius of the circle to be removed = 3 cm
∴ Area of sheet removed = πr
2
= 9π cm
2
Area of the remaining sheet
= (16π – 9π) cm2 = 7π cm
2
= 7 × 3.14 cm
2
= 21.98 cm
2
Hence, the required area = 21.98 cm
2
.
Ex 11.3 Class 7 Maths Question 6.
Saima wants to put a lace on the edge of a circular table cover of diameter 1.5 m. Find the length of the lace required and also find its cost if one metre of the lace costs ₹ 15. (Take π = 3.14)
Solution:
Diameter of the table cover = 1.5 m
∴ Radius = \(\frac{1.5}{2}\) = 0.75 m
∴ Length of the lace = 2πr = 2 × 3.14 × 0.75
= 4.710 m
Cost of the lace = ₹ 15 × 4.710 = ₹ 70.65
Ex 11.3 Class 7 Maths Question 7.
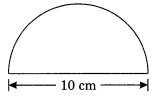
Find the perimeter of the given figure, which is a semicircle including its diameter.
Solution:
Given: Diameter = 10 cm

Hence, the required perimeter
= 25.7 cm. (approx.)
Ex 11.3 Class 7 Maths Question 8.
Find the cost of polishing a circular table-top of diameter 1.6 m, if the rate of polishing is ₹ 15 m
2
. (Take π = 3.14)
Solution:
Given:
Diameter = 1.6 m
∴ Radius = \(\frac{1.6}{2}\) = 0.8 m
Area of the table-top = πr
2
= 3.14 × 0.8 × 0.8 m
2
= 2.0096 m
2
∴ Cost of polishing = ₹ 15 × 2.0096
= ₹ 30.14 (approx.)
Ex 11.3 Class 7 Maths Question 9.
Shazli took a wire of length 44 cm and bent it into the shape of a circle. Find the radius of that circle. Also find its area. If the same wire is bent into the shape of a square, what will be the length of each of its sides? Which figure encloses more area, the circle or the square? (Take π =\(\frac{22}{7}\))
Solution:
Length of the wire to be bent into a circle = 44 cm
2πr = 44
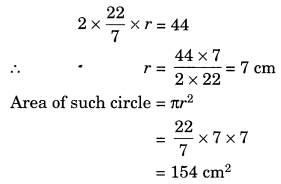
Now, the length of the wire is bent into a square.
Here perimeter of square
= Circumference of line k
Length of each side of the square
\(=\frac{\text { Perimeter }}{4}=\frac{44}{4}=11 \mathrm{cm}\)
Area of the square = (Side)
2
= (11)
2
= 121 cm
2
Since, 154 cm
2
>121 cm
2
Thus, the circle encloses more area.
Ex 11.3 Class 7 Maths Question 10.
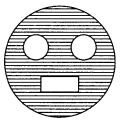
From a circular card sheet of radius 14 cm, two circles of radius 3.5 cm and a rectangle of length 3 cm and breadth 1 cm are removed, (as shown in the given figure below). Find the area of the remaining sheet. (Take π = \(\frac{22}{7}\))
Solution:
Radius of the circular sheet = 14 cm
∴ Area = πr
2
= \(\frac{22}{7}\) × 14 × 14 cm
2
= 616 cm
2
Area of 2 small circles = 2 × πr
2
= 2 × \(\frac{22}{7}\) × 3.5 × 3.5 cm
2
= 77.0 cm
2
Area of the rectangle = l × b
= 3 × 1 cm
2
= 3 cm
2
Area of the remaining sheet after removing the 2 circles and 1 rectangle
= 616 cm
2
– (77 + 3) cm
2
= 616 cm
2
– 80 cm
2
= 536 cm
2
Ex 11.3 Class 7 Maths Question 11.
A circle of radius 2 cm is cut out from a square piece of an aluminium sheet of side 6 cm. What is the area of the left over aluminium sheet? (Take π = 3.14)
Solution:
Side os the square sheet = 6 m
∴ Area of the sheet = (Side)
2
= (6)
2
= 36 cm
2
Radius of the circle = 2 cm
∴ Area of the circle to be cut out = πr
2
= \(=\frac{22}{7} \times 2 \times 2=\frac{88}{7} \mathrm{cm}^{2}\)
Area of the left over sheet
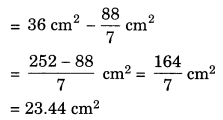
Ex 11.3 Class 7 Maths Question 12.
The circumference of a circle is 31.4 cm. Find the radius and the area of the circle. (Take π = 3.14)
Solution:
Circumference of the circle = 31.4 cm
2πr = 31.4
∴ \(r=\frac{31.4}{2 \times 3.14}\) = 5cm
Area of the circle = 7πr
2
= 3.14 × 5 × 5 = 78.5 cm
2
Hence, the required radius = 5 cm and area = 78.5 cm
2
.
Ex 11.3 Class 7 Maths Question 13.
A circular flower bed is surrounded by a path 4 m wide. The diameter of the flower bed is 66 m. What is the area of this path? (Take π = 3.14)
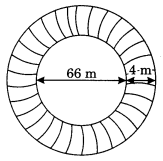
Solution:
Diameter of the flower bed = 66 m .
∴ Radius = \(\frac{66}{2}\) = 33 m
Let r
1
= 33 m
Width of the path = 4 m
Radius of the flower bed included path
= 33 m + 4 m = 37m
Let r
2
= 37m
Area of the circular path = \(\pi\left(r_{2}^{2}-r_{1}^{2}\right)\)
= 3.14 (37
2
– 33
2
)
= 3.14 × (37 + 33) (37 – 33) [Y a
2
– b
2
= (a + b)(a-b)]
= 3.14 × 70 × 4 = 879.20 m
2
Hence, the required area = 879.20 m
2
Ex 11.3 Class 7 Maths Question 14.
A circular flower garden has an area of 314 m
2
. A sprinkler at the centre of the garden can cover an area that has a radius of 12 m. Will the sprinkler can water the entire garden?
[Take π = 3.14]
Solution:
Area of the flower garden = 314 m
2
Radius of the circular portion covered by the sprinkler = 12 m
∴ Area = 7πr
2
= 3.14 × 12 × 12
= 3.14 × 144 m
2
= 452.16 m
2
Since 452.16 m
2
> 314 m
2
Yes, the sprinkler will water the entire garden.
Ex 11.3 Class 7 Maths Question 15.
Find the circumference of the inner and the outer circles, shown in the given figure. (Take π = 3.14)
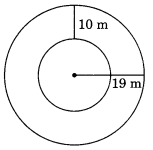
Solution:
Radius of the outer circle = 19 m
∴ Circumference of the outer circle = 2πr
= 2 × 3.14 × 19 = 3.14 × 38 m
= 119.32 m
Radius of the inner circle
= 19m – 10m = 9m
∴ Circumference = 2πr = 2 × 3.14 × 9
= 56.52 m
Here the required circumferences are 56.52 m and 119.32 m.
Ex 11.3 Class 7 Maths Question 16.
How many times a wheel of radius 28 cm must rotate to go 352 m? (Take π = \(\frac{22}{7}\))
Solution:
Radius of the wheel = 28 cm
∴ Circumference = 2πr = 2 × \(\frac{22}{7}\) × 28 = 176 cm
Number of rotations made by the wheel in going 352 m or 35200 cm
\(=\frac{35200}{176}=200\)
Hence, the required number of rotation = 200.
Ex 11.3 Class 7 Maths Question 17.
The minute hand of a circular clock is 15 cm long. How far does the tip of the minute hand move in 1 hour? (Take π = 3.14)
Solution:
Length of minute hand = 15 cm
∴ Radius = 15 cm
Circumference = 2πr
= 2 × 3.14 × 15 cm = 94.2 cm
Since the minute hand covers the distance in 1 hour equal to the circumference of the circle. Here the required distance covered by the minute hand = 94.2 cm.







NCERT Solutions Maths Science Social English Sanskrit Hindi RD Sharma