NCERT Solutions for Class 12 Maths Chapter 13 Probability Ex 13.5
The topics and sub-topics included in Chapter 13 Probability the following:
| Section Name | Topic Name |
| 13 | Probability |
| 13.1 | Introduction |
| 13.2 | Conditional Probability |
| 13.3 | Multiplication Theorem on Probability |
| 13.4 | Independent Events |
| 13.5 | Bayes’ Theorem |
| 13.6 | Random Variables and its Probability Distributions |
| 13.7 | Bernoulli Trials and Binomial Distribution |
NCERT Solutions for Class 12 Maths Chapter 13 Probability 13.5 are part of NCERT Solutions for Class 12 Maths . Here we have given Class 12 Maths NCERT Solutions Probability Ex 13.5
Class 12 Maths Probability Solutions
- Probability Class 12 NCERT Solutions Ex 13.1
- Probability Class 12 NCERT Solutions Ex 13.2
- Probability Class 12 NCERT Solutions Ex 13.3
- Probability Class 12 NCERT Solutions Ex 13.4
Question 1.
A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of
(i) 5 successes?
(ii) at least 5 successes?
(iii) at most 5 successes?
Solution:
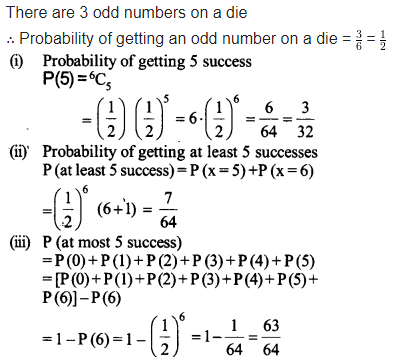
Question 2.
There are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item ?
Solution:

Question 3.
A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability, of two successes.
Solution:
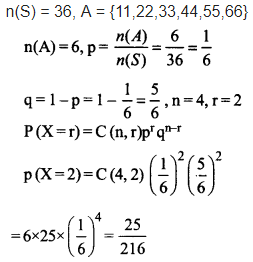
Question 4.
Five cards are drawn successively with replacement from a well- shuffled deck of 52 cards. What is the probability that
(i) all the five cards are spades?
(ii) only 3 cards are spades?
(iii) none is spade?
Solution:
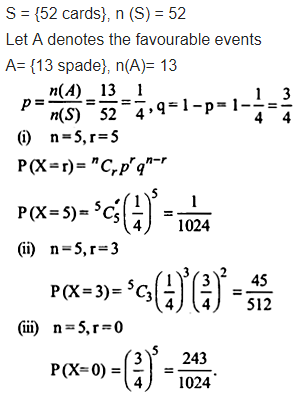
Question 5.
The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs.
(i) none
(ii) not more than one
(iii) more than one
(iv) at least one will fuse after 150 days of use
Solution:

Question 6.
A bag consists of 10 balls each marked with one of the digits 0 to 9. If four bails are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?
Solution:

Question 7.
In an examination, 20 questions of true – false type are asked. Suppose a student tosses fair coin to determine his answer to each question. If the coin falls heads, he answers ‘true,’ if it falls tails, he answers “ false’. Find the probability that he answers at least 12 questions correctly.
Solution:

Question 8
Suppose X has a binomial distribution \(B\left( 6,\frac { 1 }{ 2 } \right) \). Show that X = 3 is the most likely outcome.
(Hint: P (X = 3) is the maximum among all P (Xi), xi. = 0,1,2,3,4,5,6)
Solution:
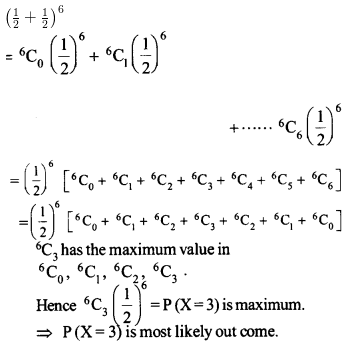
Question 9.
On a multiple choice examination with three possible answers for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing?
Solution:
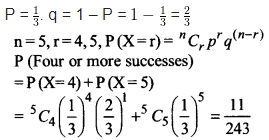
Question 10.
A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is \(\frac { 1 }{ 100 }\) . What is the probability that he will win a prize?
(a) at least once,
(b) exactly once,
(c) at least twice?
Solution:

Question 11.
Find the probability of getting 5 exactly twice in 7 throws of a die.
Solution:
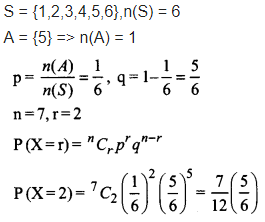
Question 12.
Find the probability of throwing at most 2 sixes in 6 throws of a single die.
Solution:
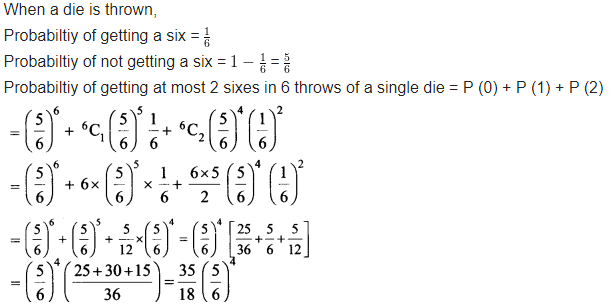
Question 13.
It is known that 10% of certain articles manufactured are defective. What is the probability that in a random sample of 12 such articles 9 are defective?
Solution:
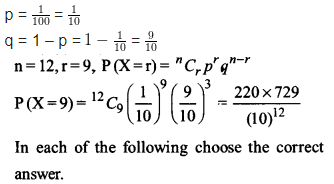
Question 14.
In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is
(a) \({ 10 }^{ -1 }\)
(b) \({ \left( \frac { 1 }{ 2 } \right) }^{ 5 }\)
(c) \({ \left( \frac { 9 }{ 10 } \right) }^{ 5 }\)
(d) \(\frac { 9 }{ 10 }\)
Solution:
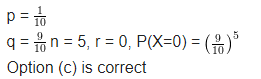
Question 15.
The probability that a student is not a swimmer is \(\frac { 1 }{ 5 }\). Then the probability that out of five students, four are swimmers is:

Solution:
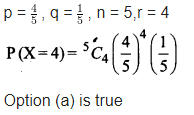
Class 12 Maths NCERT Solutions
- Chapter 1 Relations and Functions
- Chapter 2 Inverse Trigonometric Functions
- Chapter 3 Matrices
- Chapter 4 Determinants
- Chapter 5 Continuity and Differentiability
- Chapter 6 Application of Derivatives
- Chapter 7 Integrals Ex 7.1
- Chapter 8 Application of Integrals
- Chapter 9 Differential Equations
- Chapter 10 Vector Algebra
- Chapter 11 Three Dimensional Geometry
- Chapter 12 Linear Programming
- Chapter 13 Probability Ex 13.1