Conic Sections Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections All Exercises were prepared by Experienced LearnCBSE.online Teachers.
Free download NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections Ex 11.1, Ex 11.2, Ex 11.3, Ex 11.4 and Miscellaneous Exercise PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.
- शंकु परिच्छेद प्रश्नावली 11.1 का हल हिंदी में
- शंकु परिच्छेद प्रश्नावली 11.2 का हल हिंदी में
- शंकु परिच्छेद प्रश्नावली 11.3 का हल हिंदी में
- शंकु परिच्छेद प्रश्नावली 11.4 का हल हिंदी में
- शंकु परिच्छेद विविध प्रश्नावली का हल हिंदी में
- Conic Sections Class Notes
- NCERT Exemplar Class 11 Maths Conic Sections
- JEE Main Mathematics Conic Sections Previous Year Questions
NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections

Topics and Sub Topics in Class 11 Maths Chapter 11 Conic Sections:
| Section Name | Topic Name |
| 11 | Conic Sections |
| 11.1 | Introduction |
| 11.2 | Sections of a Cone |
| 11.3 | Circle |
| 11.4 | Parabola |
| 11.5 | Ellipse |
| 11.6 | Hyperbola |
National Council of Educational Research and Training (NCERT) Book Solutions for class 11th
Subject: Maths
Chapter: Chapter 11 Conic Sections
Class 11th Maths Chapter 11 Conic Sections NCERT Solution is given below.
NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.1
Ex 11.1 Class 11 Question 1:
![]()
Ans:
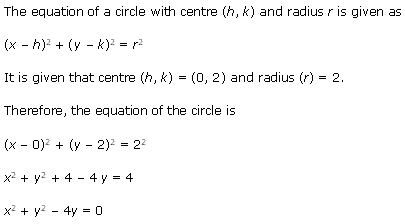
Ex 11.1 Class 11 Maths Question 2:
![]()
Ans:
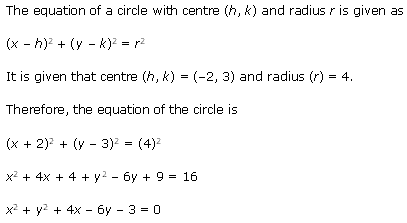
RD Sharma Class 11 Maths Solutions
Ex 11.1 Class 11 Maths Question 3:
![]()
Ans:
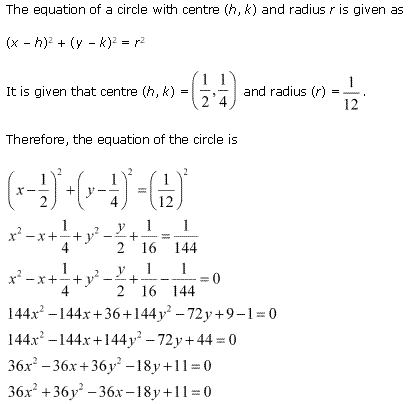
Ex 11.1 Class 11 Maths Question 4:
![]()
Ans:
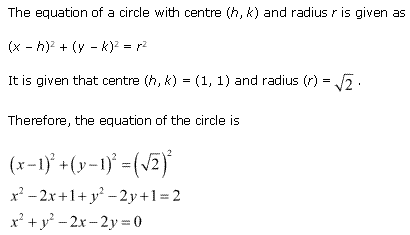
Ex 11.1 Class 11 Maths Question 5:
![]()
Ans:
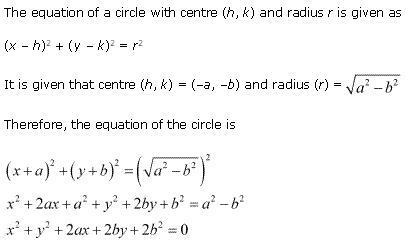
Ex 11.1 Class 11 Maths Question 6:
![]()
More Resources for CBSE Class 11
- NCERT Solutions
- NCERT Solutions Class 11 Maths
- NCERT Solutions Class 11 Physics
- NCERT Solutions Class 11 Chemistry
- NCERT Solutions Class 11 Biology
Ans:
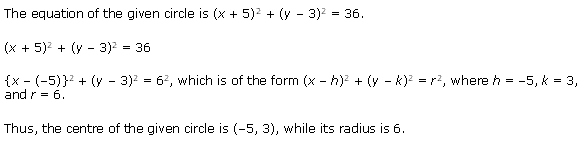
Ex 11.1 Class 11 Maths Question 7:
![]()
Ans:
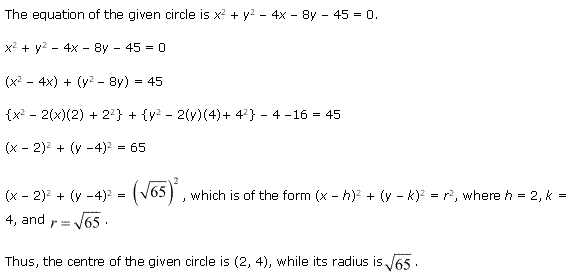
Ex 11.1 Class 11 Maths Question 8:
![]()
Ans:
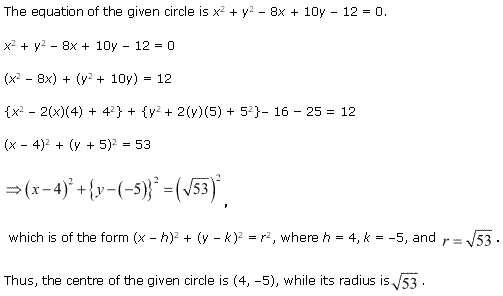
Ex 11.1 Class 11 Maths Question 9:
![]()
Ans:
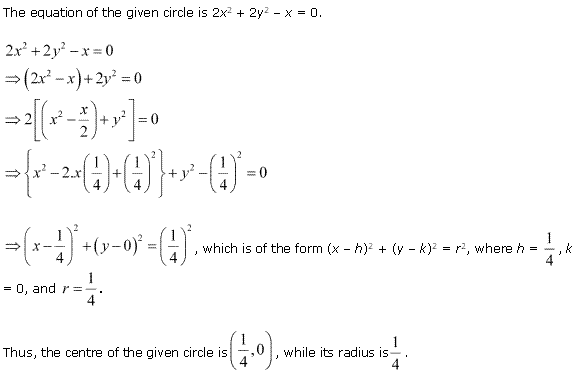
Ex 11.1 Class 11 Maths Question 10:
![]()
Ans:

Ex 11.1 Class 11 Maths Question 11:
Find the equation of the circle passing through the points (2, 3) and (-1, 1) and whose centre is on the line x – 3y – 11 = 0.
Solution:
The equation of the circle is,
(x – h)2 + (y – k)2 = r2 ….(i)
Since the circle passes through point (2, 3)
∴ (2 – h)2 + (3 – k)2 = r2
⇒ 4 + h2 – 4h + 9 + k2 – 6k = r2
⇒ h2+ k2 – 4h – 6k + 13 = r2 ….(ii)
Also, the circle passes through point (-1, 1)
∴ (-1 – h)2 + (1 – k)2 = r2
⇒ 1 + h2 + 2h + 1 + k2 – 2k = r2
⇒ h2 + k2 + 2h – 2k + 2 = r2 ….(iii)
From (ii) and (iii), we have
h2 + k2 – 4h – 6k + 13 = h2 + k2 + 2h – 2k + 2
⇒ -6h – 4k = -11 ⇒ 6h + 4k = 11 …(iv)
Since the centre (h, k) of the circle lies on the line x – 3y-11 = 0.
∴ h – 3k – 11 = 0 ⇒ h -3k = 11 …(v)
Solving (iv) and (v), we get
h = \(\frac { 7 }{ 2 } \) and k = \(\frac { -5 }{ 2 } \)
Putting these values of h and k in (ii), we get
\(\left( \frac { 7 }{ 2 } \right) ^{ 2 }+\left( \frac { -5 }{ 2 } \right) ^{ 2 }-\frac { 4\times 7 }{ 2 } -6\times \frac { -5 }{ 2 } +13={ r }^{ 2 }\)
⇒ \(\frac { 49 }{ 4 } +\frac { 25 }{ 4 } -14+15+13 \) ⇒ \({ r }^{ 2 }=\frac { 65 }{ 2 } \)
Thus required equation of circle is
⇒ \(\left( x-\frac { 7 }{ 2 } \right) ^{ 2 }+\left( y+\frac { 5 }{ 2 } \right) ^{ 2 }=\frac { 65 }{ 2 } \)
⇒ \({ x }^{ 2 }+\frac { 49 }{ 4 } -7x+{ y }^{ 2 }+\frac { 25 }{ 4 } +5y=\frac { 65 }{ 2 } \)
⇒ 4×2 + 49 – 28x + 4y2 + 25 + 20y = 130
⇒ 4×2 + 4y2 – 28x + 20y – 56 = 0
⇒ 4(x2 + y2 – 7x + 5y -14) = 0
⇒ x2 + y2 – 7x + 5y -14 = 0.
Ex 11.1 Class 11 Maths Question 12:
![]()
Ans:

Ex 11.1 Class 11 Maths Question 13:
![]()
Ans:

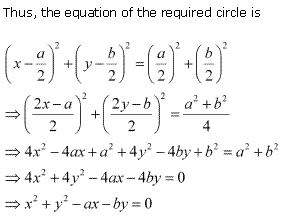
Ex 11.1 Class 11 Maths Question 14:
![]()
Ans:
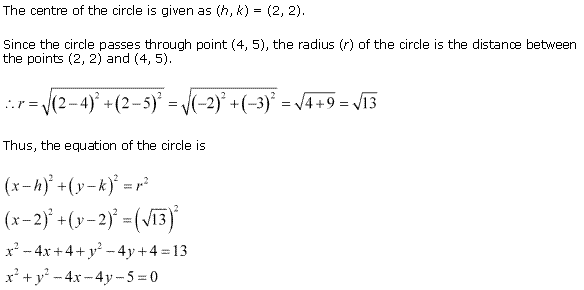
Ex 11.1 Class 11 Maths Question 15:
![]()
Ans:

NCERT Solutions for Class 11 Maths Chapter 11 Conic Sections (शंकु परिच्छेद) Hindi Medium Ex 11.1









NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.2
Ex 11.2 Class 11 Maths Question 1:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 2:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 3:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 4:
![]()
Ans:
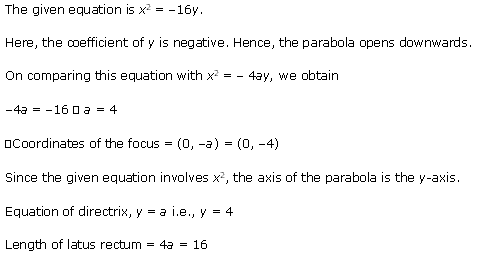
Ex 11.2 Class 11 Maths Question 5:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 6:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 7:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 8:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 9:
![]()
Ans:
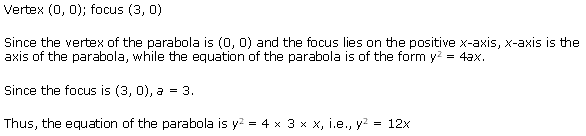
Ex 11.2 Class 11 Maths Question 10:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 11:
![]()
Ans:

Ex 11.2 Class 11 Maths Question 12:
![]()
Ans:
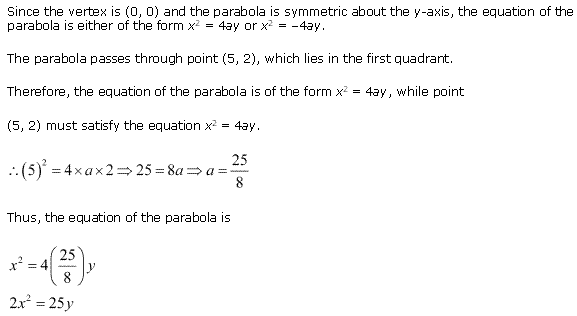
NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.3
Ex 11.3 Class 11 Maths Question 1:

Ans:

Ex 11.3 Class 11 Maths Question 2:

Ans:

Ex 11.3 Class 11 Maths Question 3:

Ans:

Ex 11.3 Class 11 Maths Question 4:

Ans:

Ex 11.3 Class 11 Maths Question 5:

Ans:

Ex 11.3 Class 11 Maths Question 6:

Ans:

Ex 11.3 Class 11 Maths Question 7:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 8:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 9:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 10:
![]()
Ans:
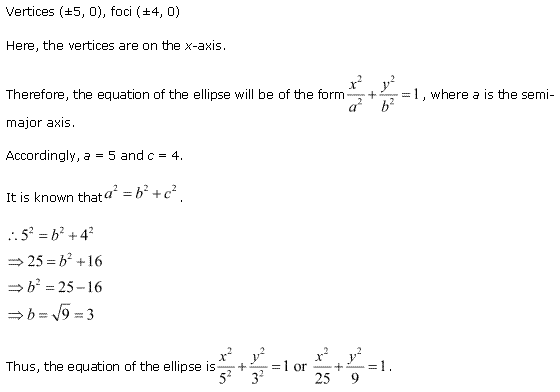
Ex 11.3 Class 11 Maths Question 11:
![]()
Ans:
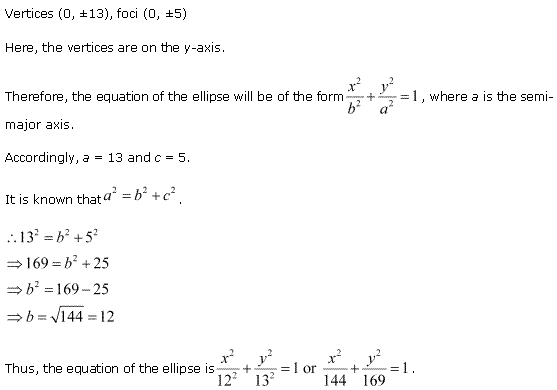
Ex 11.3 Class 11 Maths Question 12:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 13:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 14:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 15:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 16:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 17:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 18:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 19:
![]()
Ans:

Ex 11.3 Class 11 Maths Question 20:
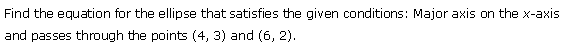
Ans:

NCERT Solutions for Class 11 Maths Chapter 11 Exercise 11.4
Ex 11.4 Class 11 Maths Question 1:

Ans:

Ex 11.4 Class 11 Maths Question 2:
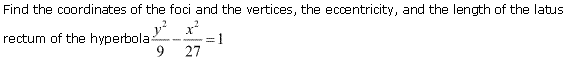
Ans:

Ex 11.4 Class 11 Maths Question 3:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 4:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 5:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 6:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 7:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 8.
Vertices (0, ±5), foci (0, ±8)
Solution:
Vertices are (0, ±5) which lie on x-axis. So the equation of hyperbola in standard form

Ex 11.4 Class 11 Maths Question 9.
Vertices (0, ±3), foci (0, ±5)
Solution:
Vertices are (0, ±3) which lie on x-axis. So the equation of hyperbola in standard form
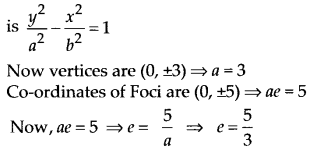
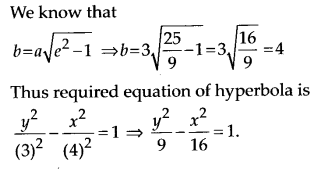
Ex 11.4 Class 11 Maths Question 10:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 11:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 12:
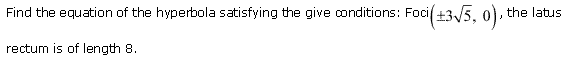
Ans:

Ex 11.4 Class 11 Maths Question 13:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 14:
![]()
Ans:

Ex 11.4 Class 11 Maths Question 15:
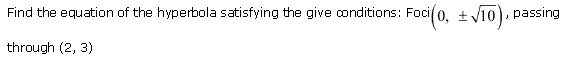
Ans:


Class 11 Maths NCERT Solutions – Miscellaneous Questions
Miscellaneous Exercise Class 11 Maths Question 1:
![]()
Ans:

Miscellaneous Exercise Class 11 Maths Question 2:
![]()
Ans:


Miscellaneous Exercise Class 11 Maths Question 3:

Ans:
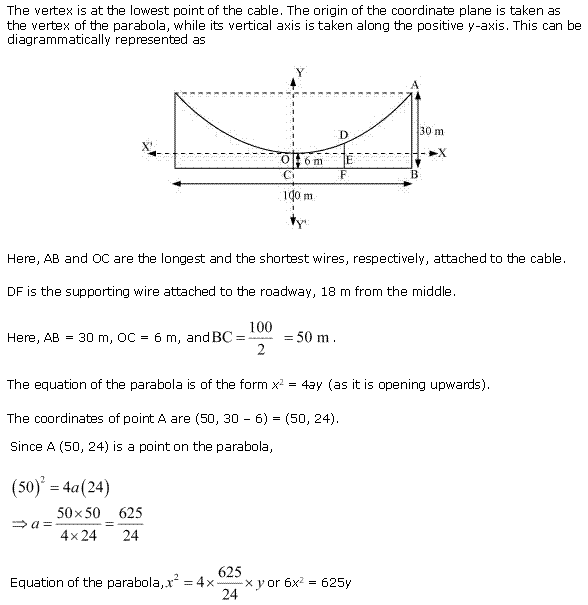

Miscellaneous Exercise Class 11 Maths Question 4:
![]()
Ans:


Miscellaneous Exercise Class 11 Maths Question 5:

Ans:

Miscellaneous Exercise Class 11 Maths Question 6:
![]()
Ans:
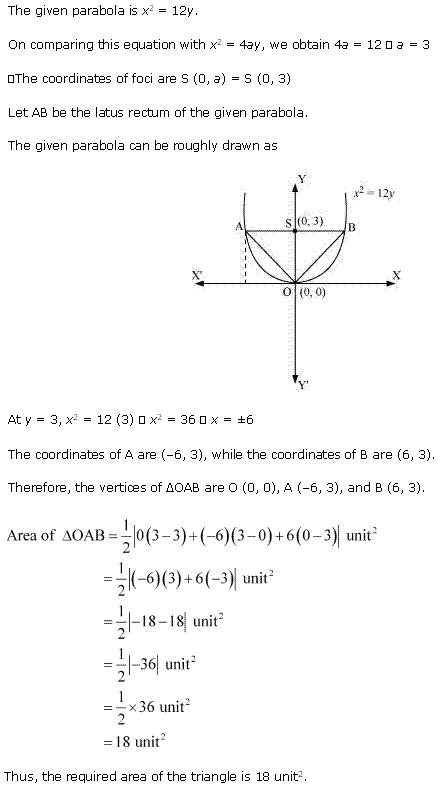
Miscellaneous Exercise Class 11 Maths Question 7:

Ans:


Miscellaneous Exercise Class 11 Maths Question 8:
![]()
Ans:
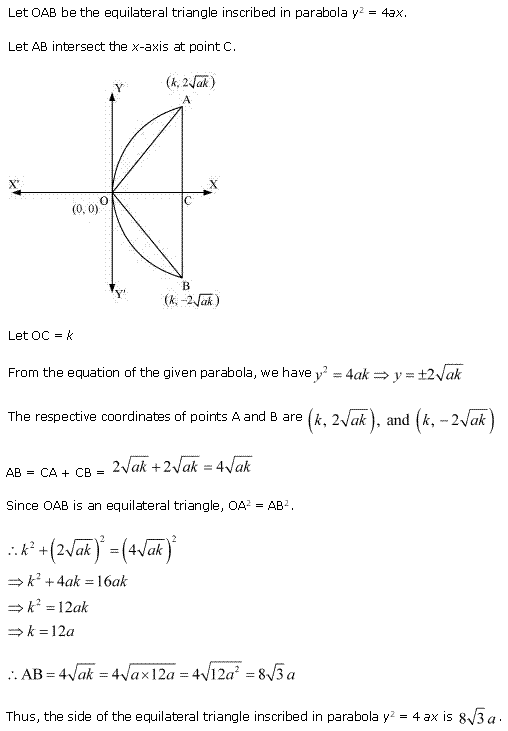
Exercise 11.1
Q.1: A circle is given with centre (0, 3) and radius 3. Obtain the equation of the given circle.
Q.2: A circle is given with centre (-1, 2) and radius 4. Find the equation of the circle.
Q.4: A circle is given with centre (2, 2) and radius √5
Q.6: The equation of a given circle is given as (a + 5) 2 + (b – 3) 2 = 36. Find the centre and radius of the circle.. Obtain the equation of the given circle.
Q.7: The equation of a given circle is given as a 2 + b 2 – 4a – 4b + 3 = 0
Find the radius and centre of the circle.
Q.8: The equation of a given circle is given as a 2 + b 2 – 6a + 8b – 14 = 0
Find the centre and radius of the circle.
Q.9: The equation of a given circle is given as 2a 2 + 2b 2 – 8a = 0
Find the centre and radius of the circle.
Q.10: The circle passing through the points (6, 2) and (4, 3) and whose centre lies on the line 2a + y = 8. Find the equation of the circle.
Q.11: The circle passing through the points (3, 2) and (-2, 2) and whose centre lies on the line a – 3y – 13 = 0. Find the equation of the circle.
Q.12: The radius of the circle is 6 whose centre lies on x – axis and passes through the point (3, 2). Find the equation.
Q.13: The circle passing through (0, 0) and making intercepts a and b on the coordinate axes. Find the equation of the circle.
Q.14: The circle with centre (3, 3) and passes through the point (6, 5), find the equation of a circle?
Q. 15: Check whether the point (–2.0, 3.0) lies inside, outside or on the circle x 2 + y 2 = 25?
Exercise 11.2
Q.1: For the equation y 2 = 16x, determine the focus coordinates, the directrix equation, the length of the latus rectum and the axis of the parabola.
Q.2: For the equation x 2 = 8y, determine the focus coordinates, the directrix equation, the length of the latus rectum and the axis of the parabola.
Q.3: For the equation y 2 = – 12x, determine the focus coordinates, the directrix equation, the length of the latus rectum and the axis of the parabola.
Q.4: For the equation x 2 = – 20y, determine the focus coordinates, the directrix equation, the length of the latus rectum and the axis of the parabola.
Q.5: For the equation y 2 = 24x, determine the focus coordinates, the directrix equation, the length of the latus rectum and the axis of the parabola.
Q.6: For the equation x 2 = – 7y, determine the focus coordinates, the directrix equation, the length of the latus rectum and the axis of the parabola.
Q7. Obtain the equation of the parabola which satisfies the given conditions below:
(i) Focus coordinates = (8, 0)
(ii) Directrix (x) = – 8
Q.8: Obtain the equation of the parabola which satisfies the given conditions below:
(i) Focus coordinates = (0, – 5)
(ii) Directrix (y) = 5
Q.9: Obtain the equation of the parabola which satisfies the given conditions below:
(i) Vertex is at origin.
(ii) Focus coordinates = (4, 0)
Q.10: Obtain the equation of the parabola which satisfies the given conditions below:
(i) Vertex is at origin.
(ii) Focus coordinates = (- 3, 0)
Q.11: Obtain the equation of the parabola which satisfies the given conditions below:
(i) Vertex is at origin.
(ii) Passing through coordinates = (3, 5)
The axis of the parabola is on x – axis.
Q.12: Obtain the equation of the parabola which satisfies the given conditions below:
(i) Vertex is at the origin.
(ii) Passing through coordinates = (6, 4)
The equation is symmetric as considered with y-axis.
Exercise 11.3
Q.7: Obtain the coordinates of the vertices, the foci, the major and the minor axis, the length of the latus rectum and the eccentricity of the ellipse 49x 2 + 9y 2 = 441
Q.8: Obtain the coordinates of the vertices, the foci, the major and the minor axis, the length of the latus rectum and the eccentricity of the ellipse 4x 2 + 16y 2 = 64
Q.9: Obtain the coordinates of the vertices, the foci, the major and the minor axis, the length of the latus rectum, and the eccentricity of the ellipse 4x 2 + y 2 = 4
Q.10: For the given condition obtain the equation of the ellipse.
(i) Vertices ( ± 6, 0)
(ii) Foci ( ± 3, 0)
Q.11: For the given condition obtain the equation of the ellipse.
(i) Vertices (0, ± 8)
(ii) Foci ( 0, ± 4)
Q.12: For the given condition obtain the equation of the ellipse.
(i) Vertices ( ± 5, 0)
(ii) Foci ( ± 3, 0)
Q.13: For the given condition obtain the equation of the ellipse.
(i) Coordinates of major axis ( ± 5, 0)
(ii) Coordinates of minor axis (0, ± 3)
Q.14: For the given condition obtain the equation of the ellipse.
(i) Coordinates of major axis (0, ± 2)
(ii) Coordinates of minor axis ( ± √3 , 0)
Q.15: For the given condition obtain the equation of the ellipse.
(i) Length of major axis 30
(ii) Coordinates of foci ( ± 4, 0)
Q.16: For the given condition obtain the equation of the ellipse.
(i) Length of minor axis 26
(ii) Coordinates of foci (0, ± 9)
Q.17: For the given condition obtain the equation of the ellipse.
(i) Coordinates of foci ( ± 4, 0)
(ii) m = 6
Q.18: For the given condition obtain the equation of the ellipse.
(i) n = 2, c = 3 (on the x – axis)
(ii) Coordinates of centre (0, 0)
Q.19: For the given condition obtain the equation of the ellipse.
(i) Centre is at origin and major axis is along the y – axis
(ii) It passes through the points (1, 6) and (3, 2)
Q.20: For the given condition obtain the equation of the ellipse.
(i) Major axis is represented along x – axis
(ii) It passes through the points (6, 2) and (4, 3)
Exercise 11.4
Q.3: Obtain the coordinates of the vertices, the foci, the length of the latus rectum and the eccentricity of the hyperbola 25 y 2 – 4 x 2 = 100
Q.4: Obtain the coordinates of the vertices, the foci, the length of the latus rectum and the eccentricity of the hyperbola 9 x 2 – 4 y 2 = 36
Q.5: Obtain the coordinates of the vertices, the foci, the length of the latus rectum and the eccentricity of the hyperbola 6 y 2 – 16 x 2 = 96
Q.6: Obtain the coordinates of the vertices, the foci, the length of the latus rectum and the eccentricity of the hyperbola 64 y 2 – 9 x 2 = 96
Q.7: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the vertices ( ± 3, 0)
(ii) Coordinates of the foci ( ± 4, 0)
Q.8: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the vertices (0, ± 7)
(ii) Coordinates of the foci (0, ± 9)
Q.9: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the vertices (0, ± 8)
(ii) Coordinates of the foci (0, ± 11)
Q.10: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the foci ( ± 7, 0),
(ii) The length of the transverse axis is 12
Q.11: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the foci (0, ± 8)
(ii) The length of the conjugate axis is 16
Q.12: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the foci ( ± 2 √3 , 0 )
(ii) The length of the latus rectum is 8
Q.13: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the foci ( ± 2 √6 , 0)
(ii) The length of the latus rectum is 10
Q.15: For the given condition obtain the equation of the hyperbola.
(i) Coordinates of the foci (0, ± √10 )
(ii) It passes through (2, 3)
NCERT Solutions for Class 11 Maths All Chapters
- Chapter 1 Sets
- Chapter 2 Relations and Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Principle of Mathematical Induction
- Chapter 5 Complex Numbers and Quadratic Equations
- Chapter 6 Linear Inequalities
- Chapter 7 Permutation and Combinations
- Chapter 8 Binomial Theorem
- Chapter 9 Sequences and Series
- Chapter 10 Straight Lines
- Chapter 11 Conic Sections
- Chapter 12 Introduction to Three Dimensional Geometry
- Chapter 13 Limits and Derivatives
- Chapter 14 Mathematical Reasoning
- Chapter 15 Statistics
- Chapter 16 Probability