NCERT Solutions for Class 11 Maths Chapter 9 Sequences and Series Miscellaneous Exercise

Get Free NCERT Solutions for Class 11 Maths Chapter 9 Sequences and Series Miscellaneous Exercise PDF in Hindi and English Medium. Sequences and Series Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Sequences and Series Miscellaneous Exercise Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.online Teachers. Detailed answers of all the questions in Chapter 9 Class 11 Sequences and Series Miscellaneous Exercise provided in NCERT Textbook.

• Sequences and Series Class 11 Ex 9.1
• Sequences and Series Class 11 Ex 9.2
• Sequences and Series Class 11 Ex 9.3
• Sequences and Series Class 11 Ex 9.4
• Sequences and Series Class 11 Miscellaneous Exercise
• अनुक्रम तथा श्रेणी प्रश्नावली 9.1 का हल हिंदी में
• अनुक्रम तथा श्रेणी प्रश्नावली 9.2 का हल हिंदी में
• अनुक्रम तथा श्रेणी प्रश्नावली 9.3 का हल हिंदी में
• अनुक्रम तथा श्रेणी प्रश्नावली 9.4 का हल हिंदी में
• अनुक्रम तथा श्रेणी विविध प्रश्नावली का हल हिंदी में
• Sequences and Series Class 11 Notes
• NCERT Exemplar Class 11 Maths Sequences and Series
• JEE Main Mathematics Sequences and Series Previous Year Questions

Free download NCERT Solutions for Class 11 Maths Chapter 9 Sequences and Series Miscellaneous Exercise PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

NCERT Solutions for Class 11 Maths Chapter 9 Sequences and Series Miscellaneous Exercise

Question 1:
Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.
Ans:

Question 2:
If the sum of three numbers in AP is 24 and their product is 440, find the numbers.
Ans:
Let the three numbers in A.P. be a – d, a, and a + d.
According to the given information,
(a – d) + (a) + (a + d) = 24
3a = 24
⇒ a = 8
and (a – d) a (a + d) = 440 ………………(ii)
(8 – d) (8) (8 + d) = 440
(8 – d) (8 + d) = 55
= 64 – d ² = 55
d ² = 64 – 55 = 9
d = ±3
Therefore, when d = 3, the numbers are 5, 8 and 11 and when d = – 3, the numbers are 11, 8 and 5.
Thus, the three numbers are 5, 8 and 11.

Question 3:
Let the sum of n, 2n, 3n terms of an A.P. be S ₁ , S ₂ and S ₃ , respectively, show that S ₃ = 3 (S ₂ – S ₁ ).
Ans:

Hence, S ₃ = 3 (S ₂ – S ₁ )

Question 4:
Find the sum of all numbers between 200 and 400 which are divisible by 7.
Ans:

S _n = \(\frac{n}{2}\) [2a + (n – 1) d]
S ₂₉ = \(\frac{29}{2}\) [2 × 203 + (29 – 1) 7]
= \(\frac{29}{2}\) [406 + 28 × 7]
= \(\frac{29}{2}\) [406 + 196]
= \(\frac{29}{2}\) × 602 2 2 2
= 29 × 301 = 8729.

Question 5:
Find the sum of integers from 1 to 100 that are divisible by 2 or 5.
Ans:

Question 6:
Find the sum of all two digit numbers which when divided by 4, yields 1 as remninder.
Ans:
The sum of two digit numbers divisible by 4 yield 1 as remainder is 13 + 17 + 21 + ………… + 97.
Let the sum be denoted by S and let 97 be the nth term.
∴ T _n = a + (n – 1) d
97 = a + (n – 1) d
= 13 + (n – 1) 4
⇒ 97 = 13 + 4n – 4
⇒ 97 – 9 = 4n
⇒ n = 22
∴ The sum, S _n = 13 + 17 + 21 + ………….+ 97
∴ S _n = \(\frac{n}{2}\) [2a + (n – 1)d]
= \(\frac{22}{7}\) [2 × 13 + (22 – 1) × 4]
= 11 [26 + 21 × 4]
= 11 [26 + 84]
= 11 × 110 = 1210

Question 7:

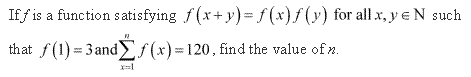
Ans:
It is given that,
f(x + y) = f(x) × f(y) for all x, y ∈ N
f(1) = 3
Taking x = y = 1 in eq. (i), we obtain
f(1 + 1) = f(2) = f(1)
f(1) = 3 × 3 = 9
Similarly, f(1 + 1 + 1) = f(3) = f(1 + 2) = f(1) f(2) = 3 × 9 = 27
f(4) = f(1 + 3) = f(1) f(3) = 3 × 27 = 81
f(1), f(2), f(3) , that is 3, 9, 27, …………, forms a G.P. with both the first term and common ratio equal to 3.
It is known that, S _n = \(\frac{a\left(r^{n}-1\right)}{r-1}\)
It is given that, \(\sum_{x=1}^{n}\) f(x) = 120
∴ 120 = \(\frac{3\left(3^{n}-1\right)}{3-1}\)

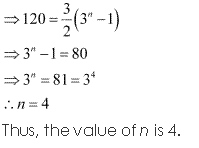
Question 8:
The sum of some terms of G.P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.
Ans:
Let the sum of n terms of the G.P. be 315.
It is known that, S ⁿ = \(\frac{a\left(r^{n}-1\right)}{r-1}\)
It is given that the first term a is 5 and common ratio r is 2.
315 = \(\frac{5\left(2^{n}-1\right)}{2-1}\)
⇒ 2n = 64 = (2) ⁶
⇒ n = 6
∴ Last term of the G.P.= 6th term
= ar ^{6 – 1} = (5) (2) ⁵ = (5) (32) = 160
Thus, the last term of the G.P. is 160.

Question 9:
The first term of a G.P. is 1. The sum of the third term and fifth term is 90. Find the common ratio of G.P.
Ans:

Question 10:
The sum of three numbers in G.P. is 56. If we subtract 1, 7, 21 from these numbers in that order, we obtain an arithmetic progression. Find the numbers.
Ans:
Let the three numbers in G.P. be a, ar and ar ² .
From the given condition, a + ar + ar ² = 56
a (1 + r + r ² ) = 56
a = \(\frac{56}{1+r+r^{2}}\) …………………(i)
a – 1, ar – 7, ar ² – 21 forms an A.P.
∴ (ar – 7) – (a – 1) = (ar ² – 21) – (ar – 7)
⇒ ar – a – 6 = ar ² – ar – 14
⇒ ar ² – 2ar + a = 8
⇒ ar ² – ar – ar + a = 8
a(r ² + 1 – 2r) = 8
a(r – 1) ² = 8 ………….(ii)
\(\frac{56}{1+r+r^{2}}\) (r – 1) ² = 8 [using eq. (1)]
⇒ 7 (r ² – 2r + 1) = 1 + r + r ²
⇒ 7r ² – 14r + 7 – 1 – r – r ² = 0
⇒ 6r ² – 15r + 6 = 0
⇒ r ² – 12r – 3r + 6 = 0
⇒ 6r (r – 2) – 3 (r – 2) = 0
⇒ (6r – 3)(r – 2) = 0
∴ r = 2, \(\frac{1}{2}\)
When r = 2, a = 8; When r = \(\frac{1}{2}\), a = 32
Therefore, when r = 2, the three numbers in G.P. are 8, 16 and 32.
When r = \(\frac{1}{2}\), the three numbers in G.P. are 32, 16 and 8.
Thus, in either case, the three required numbers are 8, 16, and 32.

Question 11:
A G.P. consists of an even number of terms. If the sum of all the terms is 5 times the sum of terms occupying odd places, then find its common ratio.
Ans:

Question 12:
The sum of the first four terms of an A.P. is 56. The sum of the last four terms is 112. If its first term is 11, then find the number of terms.
Ans:
Let the A.P. be a, a + d, a + 2d, a + 3d,… a + (n – 2) d, a + (n – 1 )d
Sum of first four terms = a + (a + d) + (a + 2d) + (a + 3d) = 4a + 6d
Sum of last four terms = [a + (n – 4) d] + [a +(n – 3) d] + [a + (n – 2) d] + [(a + n – 1) d]
= 4a + (4n – 10)d
According to the given condition,
4a + 6d = 56
⇒ 4 (11) + 6d = 56 [Since a = 11 (given)]
⇒ 6d = 12
⇒ d = 2
4a + (4n – 10) d = 112
⇒ 4(11) + (4n – 10) 2 = 112
⇒ (4n – 10)2 = 68
⇒ 4n – 10 = 34
4n = 44
n = 11
Thus, the number of terms of the A.P. is 11.

Question 13:
If \(\frac{a+b x}{a-b x}=\frac{b+c x}{b-c x}=\frac{c+d x}{c-d x}\), then show that a, b, c and d are in G.P.
Ans:

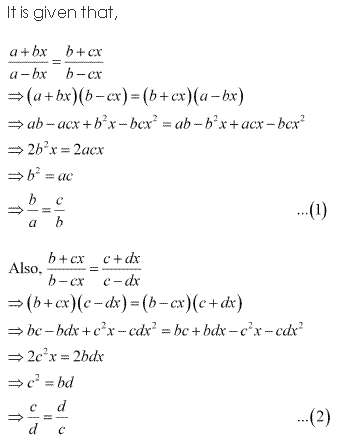
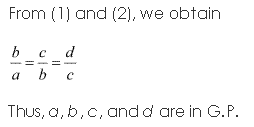
Question 14:
Let S be the sum, P the product and R the sum of reciprocal of n terms in a G.P. Prove that P ² R ⁿ = S ⁿ .
Ans:
Let the G.P. be a, ar, ar ² , ar ³ , ………….., ar ^{n – 1}
According to the given information,
S = \(\frac{a\left(r^{n}-1\right)}{r-1}\)
P = a ⁿ r ^{\(\frac{n(n-1)}{2}\)}
[∵ Sum of n natural numbers is n \(\frac{(n+1)}{2}\)]

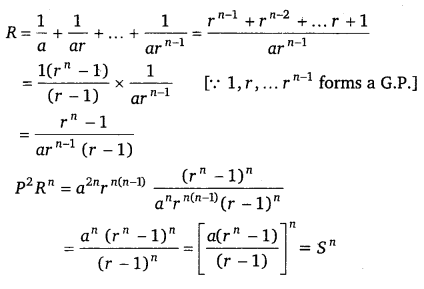
Hence P ² R ⁿ = S ⁿ .

Question 15:
The th, qth and rth terms of an AP. are a, b, c respectively. Show that(q – r)a + (r – p) b + (p – q) c = 0.
Ans:
Let A be the first term and d be the common difference.
Since, T _p = a
⇒ A + (p – 1) d = a ……………(i)
T _q = b
⇒ A + (q – 1) d = b …………….(ii)
and T _r = c
⇒ A + (r – 1) d = c ……………..(iii)
(i) On multiplying eq. (i) by (q – r), eq. (ii) by (r – p) and eq. (iii) by (p – q),we get
(q – r) A + (p – 1) (q – r) d = a (q – r) …………..(iv)
(r – p) A + (q – 1) (r – p) d = b (r – p) …………….(v)
and (p – q) A + (r – 1) (p – q) d = c (p – q) ……………(vi)
On adding eqs. (iv), (v) and eq. (vi), we get
(q – r) A + (p – 1) (q – r) d + (r – p) A + (q – 1) (r – p) d + (p – q) A + (r – 1) (p – q) d = a (q – r) + b (r – p) + c (p – q)
⇒ A [(q – r) + (r – p) + (p – q)] + (p – 1) (q – r) + (q – 1) (r – p) + (r – 1) (p – q)] d = a (q – r) + b (r – p) + c (p – q)
A(0) + (0)d = a (q – r) + b (r – p) + c (p – q)
a (q – r) + b (r – p) + c (p – q) = 0
Hence proved.

Question 16:
If \(a\left(\frac{1}{b}+\frac{1}{c}\right), b\left(\frac{1}{c}+\frac{1}{a}\right), c\left(\frac{1}{a}+\frac{1}{b}\right)\) are in A.P.,prove that a, b, c are in A.P.
Ans:

It is given that \(a\left(\frac{1}{b}+\frac{1}{c}\right), b\left(\frac{1}{c}+\frac{1}{a}\right), c\left(\frac{1}{a}+\frac{1}{b}\right)\) are in A.P.

∴ \(b\left(\frac{1}{c}+\frac{1}{a}\right)-a\left(\frac{1}{b}+\frac{1}{c}\right)=c\left(\frac{1}{a}+\frac{1}{b}\right)-b\left(\frac{1}{c}+\frac{1}{a}\right)\)

⇒ \(\frac{b(a+c)}{a c}-\frac{a(b+c)}{b c}=\frac{c(a+b)}{a b}-\frac{b(a+c)}{a c}\)

⇒ \(\frac{b^{2} a+b^{2} c-a^{2} b-a^{2} c}{a b c}=\frac{c^{2} a+c^{2} b-b^{2} a-b^{2} c}{a b c}\)

⇒ b ² a – a ² b + b ² c – a ² c = c ² a – b ² a + c ² b – b ² c
⇒ ab (b – a) + c (b ² – a ² ) = a (c ² – b ² ) + bc (c – b)
⇒ ab (b – a) + c (b – a) (b + a) = a (c – b) (c + b) + bc (c – b)
⇒ (b – a) (ab + cb + ca) = (c – b) (ac + ab + bc)
⇒ b – a = c – b
Thus, a, b and c are in A.P.

Question 17:
If a, b, c, d are in G.P. prove that (a ⁿ + b ⁿ ), (b ⁿ + c ⁿ ), (c ⁿ + d ⁿ ) are in G.P.
Ans:

Question 18:
If a and b are the roots of x ² – 3x + p = 0 and c, d are roots of x ² – 12x + q = 0, where a, b, c, d form a G.P. Prove that (q + p) : (q – p) = 17 : 15.
Ans:

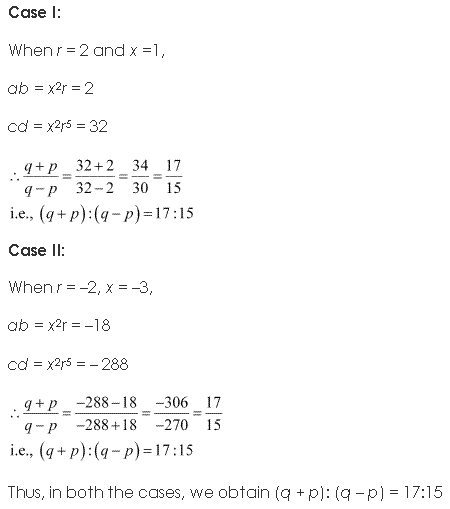
Question 19:
The ratio of the A.M. and G.M. of two positive numbers a and b, is m : n. Show that a : b (m + \(\sqrt{m^{2}-n^{2}}\)) : (m – \(\sqrt{m^{2}-n^{2}}\)).
Ans:

Question 20:

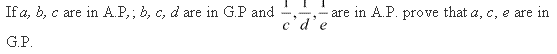
Ans:

Question 21:
Find the sum of the following series up to n terms.
(i) 5 + 55 + 555 + ……………
(ii) .6 + .66 + .666 + ……………
Ans:

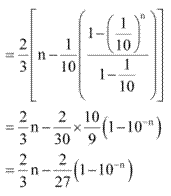
Question 22:

Ans:

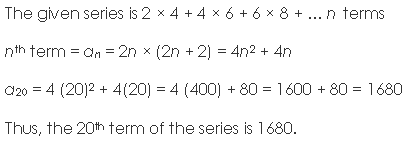
Question 23:

Ans:

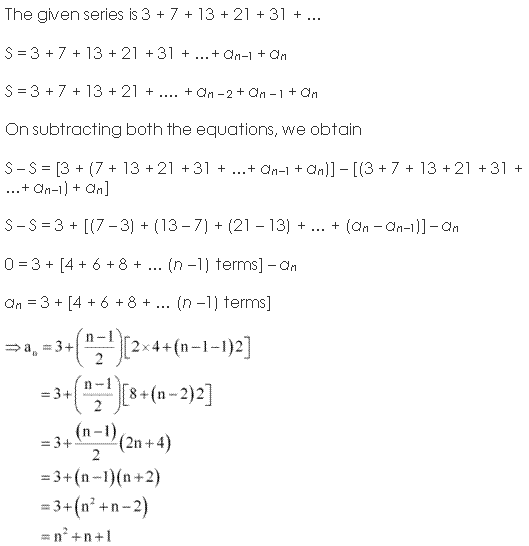
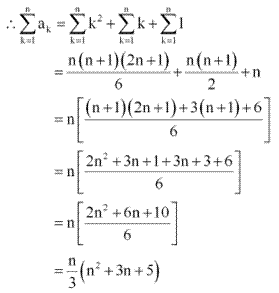
Question 24:

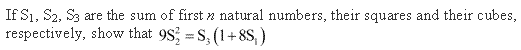
Ans:

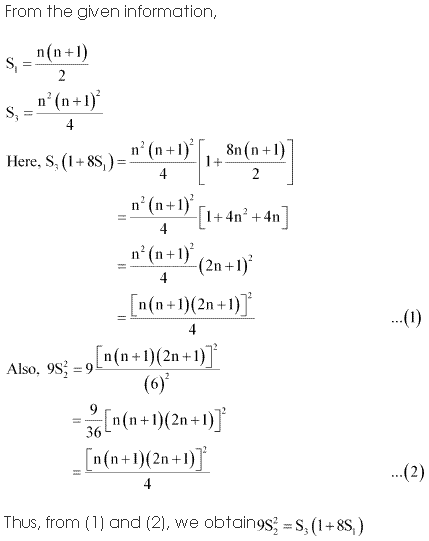
Question 25:

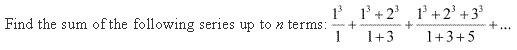
Ans:

Question 26:

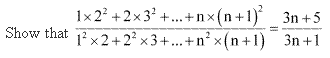
Ans:

Question 27:
A farmer buys a used tractor for Rs. 12000. He pays Rs. 6000 cash and agrees to pay the balance in annual installments of Rs. 500 plus 12% interest on the unpaid amount. How much will be the tractor cost him?
Ans:

Question 28:
Shamshad Ali buys a scooter for Rs. 22000. He pays Rs. 4000 cash and agrees to pay the balance in annual installment of Rs. 1000 plus 10% interest on the unpaid amount. How much will the scooter cost him?
Ans:

Question 29:
A person writes a letter to four of his friends. He asks each one of them to copy the letter and mail to four different persons with instruction that they move the chain similarly. Assuming that the chain is not broken and that it costs 50 paise to mail one letter. Find the amount spent on the postage when 8th set of letter is mailed.
Ans:

Question 30:
A man deposited Rs. 10000 in a bank at the rate of 5% simple interest annually. Find the amount in 15 ^th year since he deposited the amount and also calculate the total amount after 20 years.
Ans:

Question 31:
A manufacturer reckons that the value of a machine, which costs him Rs. 15625, will depreciate each year by 20%. Find the estimated value at the end of 5 years.
Ans:

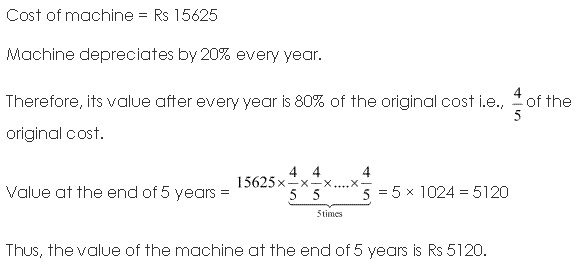
Question 32:
150 workers were engaged to finish a job in a certain number of days. 4 workers dropped out on second day, 4 more workers dropped out on third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed.
Ans:

NCERT Solutions for Class 11 Maths Chapter 9 Sequences and Series (अनुक्रम तथा श्रेणी) Miscellaneous Exercise Hindi Medium

NCERT Solutions for Class 11 Maths All Chapters

• Chapter 1 Sets
• Chapter 2 Relations and Functions
• Chapter 3 Trigonometric Functions
• Chapter 4 Principle of Mathematical Induction
• Chapter 5 Complex Numbers and Quadratic Equations
• Chapter 6 Linear Inequalities
• Chapter 7 Permutation and Combinations
• Chapter 8 Binomial Theorem
• Chapter 9 Sequences and Series
• Chapter 10 Straight Lines
• Chapter 11 Conic Sections
• Chapter 12 Introduction to Three Dimensional Geometry
• Chapter 13 Limits and Derivatives
• Chapter 14 Mathematical Reasoning
• Chapter 15 Statistics
• Chapter 16 Probability

AI CONTENT END 1 <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#" xmlns:dc="http://purl.org/dc/elements/1.1/" xmlns:trackback="http://madskills.com/public/xml/rss/module/trackback/"> <rdf:Description rdf:about="https://www.LearnCBSE.online/ncert-solutions-for-class-11-maths-chapter-9-miscellaneous-exercise/" dc:identifier="https://www.LearnCBSE.online/ncert-solutions-for-class-11-maths-chapter-9-miscellaneous-exercise/" dc:title="NCERT Solutions for Class 11 Maths Chapter 9 Sequences and Series Miscellaneous Exercise" trackback:ping="https://www.LearnCBSE.online/ncert-solutions-for-class-11-maths-chapter-9-miscellaneous-exercise/trackback/" /> </rdf:RDF>