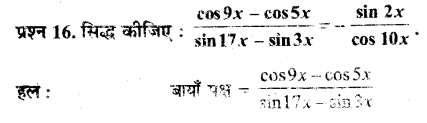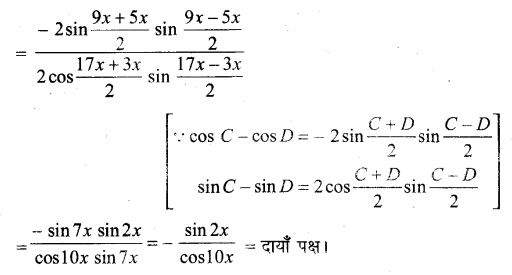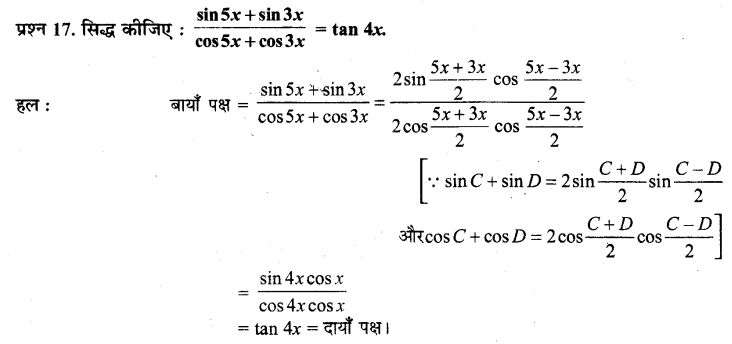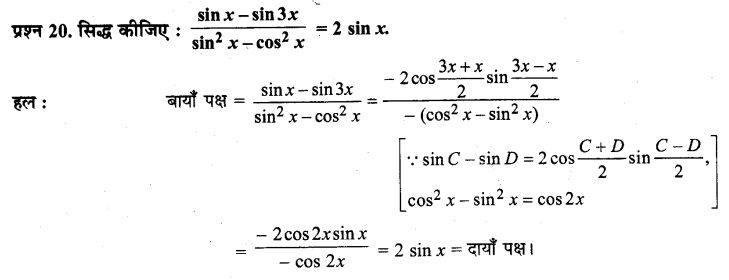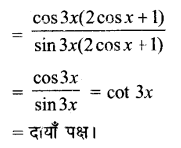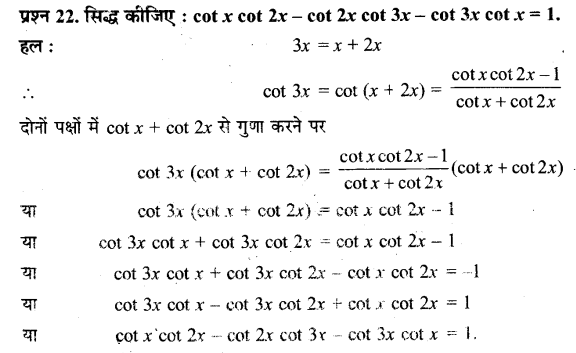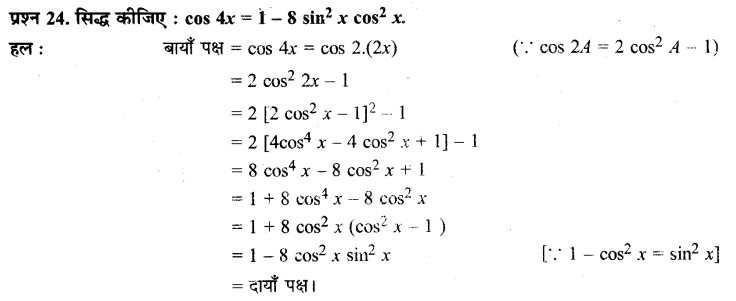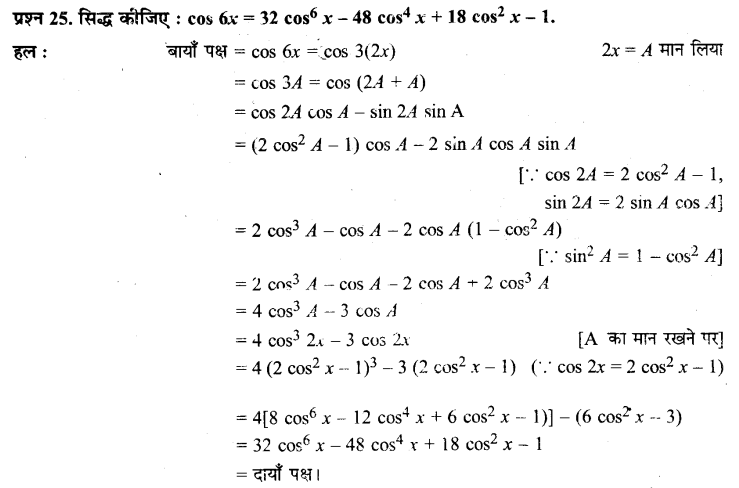NCERT Solutions for Class 11 Maths Chapter 3 Ex 3.3

Get Free NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.3 PDF in Hindi and English Medium. Trigonometric Functions Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Trigonometric Functions Exercise 3.3 Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.online Teachers. Detailed answers of all the questions in Chapter 3 Class 11 Trigonometric Functions Ex 3.3 provided in NCERT Textbook.

• Trigonometric Functions Class 11 Ex 3.1
• Trigonometric Functions Class 11 Ex 3.2
• Trigonometric Functions Class 11 Ex 3.3
• Trigonometric Functions Class 11 Ex 3.4
• Trigonometric Functions Class 11 Miscellaneous Exercise
• त्रिकोणमितीय फलन प्रश्नावली 3.1 का हल हिंदी में
• त्रिकोणमितीय फलन प्रश्नावली 3.2 का हल हिंदी में
• त्रिकोणमितीय फलन प्रश्नावली 3.3 का हल हिंदी में
• त्रिकोणमितीय फलन प्रश्नावली 3.4 का हल हिंदी में
• त्रिकोणमितीय फलन विविध प्रश्नावली का हल हिंदी में
• Trigonometry Formulas
• Trigonometry Functions Class 11 Notes
• NCERT Exemplar Class 11 Maths Chapter 3 Trigonometric Functions
• Trig Cheat Sheet
• JEE Main Trigonometry Previous Year Questions

Free download NCERT Solutions for Class 11 Maths Chapter 3 Trigonometric Functions Ex 3.3 PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

NCERT Solutions for Class 11 Maths Chapter 3 Ex 3.3

Ex 3.3 Class 11 Maths Question 1:

Prove that: sin ² \(\frac{\pi}{6}\) + cos ² \(\frac{\pi}{3}\) – tan ² \(\frac{\pi}{4}\) = – \(\frac{1}{2}\)
Ans:

L.H.S.= sin ² \(\frac{\pi}{6}\) + cos ² \(\frac{\pi}{3}\) – tan ² \(\frac{\pi}{4}\)

= \(\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}\) – (1) ²

= \(\frac{1}{4}+\frac{1}{4}-1=-\frac{1}{2}\)

= R.H.S.
Hence proved.

Ex 3.3 Class 11 Maths Question 2:
Prove that: 2 sin ² \(\frac{\pi}{6}\) + cosec ² \(\frac{7 \pi}{6}\) cos ² \(\frac{\pi}{3}\) = \(\frac{3}{2}\)
Ans:

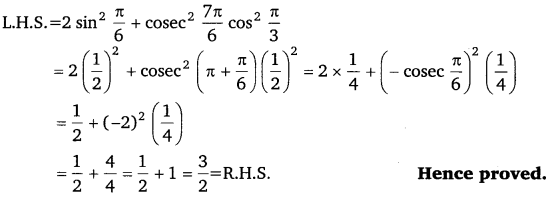
Ex 3.3 Class 11 Maths Question 3:
Prove that :cot ² \(\frac{\pi}{6}\) + cosec \(\frac{5 \pi}{6}\) + 3 tan ² \(\frac{\pi}{6}\) = 6
Ans:

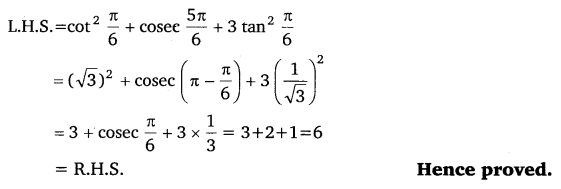
Ex 3.3 Class 11 Maths Question 4:
Prove that: 2 sin ² \(\frac{3 \pi}{4}\) + 2 cos ² \(\frac{\pi}{4}\) + 2 sec ² \(\frac{\pi}{3}\) = 10
Ans:

L.H.S = \(2 \sin ^{2} \frac{3 \pi}{4}+2 \cos ^{2} \frac{\pi}{4}+2 \sec ^{2} \frac{\pi}{3}\)

= \(2\left\{\sin \left(\pi-\frac{\pi}{4}\right)\right\}^{2}+2\left(\frac{1}{\sqrt{2}}\right)^{2}+2(2)^{2}\)

= \(2\left\{\sin \frac{\pi}{4}\right\}^{2}+2 \times \frac{1}{2}+8\)

= 2 \(\left(\frac{1}{\sqrt{2}}\right)^{2}\) + 1 + 8

= 1 + 1 + 8
= 10 = R.H.S.
Hence proved.

Ex 3.3 Class 11 Maths Question 5:
Find the value of: (i) sin 75°,
(ii) tan 15°
Ans:

(i) sin 75° sin (45° + 30°)
= sin 45° cos 30° + cos 45° sin 30°
[∵ sin (x + y) = sin x cos y + cos x sin y]
= \(\left(\frac{1}{\sqrt{2}}\right)\left(\frac{\sqrt{3}}{2}\right)+\left(\frac{1}{\sqrt{2}}\right)\left(\frac{1}{2}\right)\)

= \(\frac{\sqrt{3}}{2 \sqrt{2}}+\frac{1}{2 \sqrt{2}}=\frac{\sqrt{3}+1}{2 \sqrt{2}}\)

(ii) tan 15° = tan (45° – 30°)

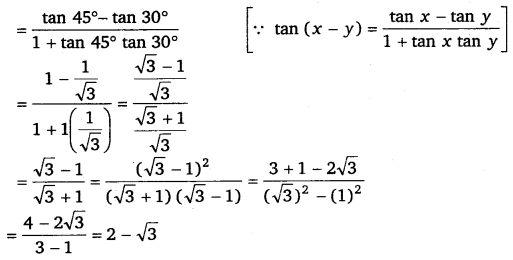
Ex 3.3 Class 11 Maths Question 6:
\(\cos \left(\frac{\pi}{4}-x\right) \cos \left(\frac{\pi}{4}-y\right)-\sin \left(\frac{\pi}{4}-x\right) \sin \left(\frac{\pi}{4}-y\right)\) = sin (x + y)
Ans:

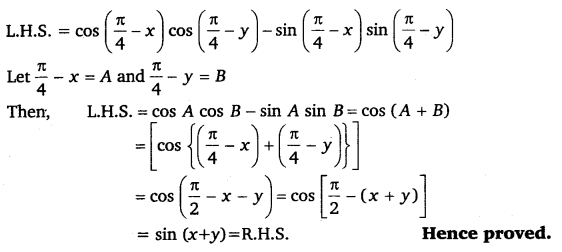
Ex 3.3 Class 11 Maths Question 7:
Prove that: \(\frac{\tan \left(\frac{\pi}{4}+x\right)}{\tan \left(\frac{\pi}{4}-x\right)}=\left(\frac{1+\tan x}{1-\tan x}\right)^{2}\)
Ans:

= \(\left(\frac{1+\tan x}{1-\tan x}\right)^{2}\)
= R.H.S
Hence proved.
Ex 3.3 Class 11 Maths Question 8:
Prove that: \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}\) = cot ² x
Ans:

L.H.S = \(\frac{\cos (\pi+x) \cos (-x)}{\sin (\pi-x) \cos \left(\frac{\pi}{2}+x\right)}\)

= \(\frac{[-\cos x][\cos x]}{(\sin x)(-\sin x)}=\frac{-\cos ^{2} x}{-\sin ^{2} x}\)

= cot ² x

= R.H.S
Hence proved.

Ex 3.3 Class 11 Maths Question 9:
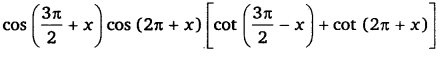= 1
Ans:

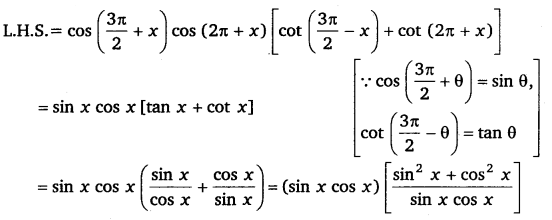
= 1 = R.H.S
Hence proved.
Ex 3.3 Class 11 Maths Question 10:
Prove that: sin (n + 1) x sin (n + 2) x + cos (n + 1) x cos (n + 2) x = cos x
Ans:
L.H. S. = sin (n + 1 )x sin (n + 2) x + cos (n +1) x cos (n + 2) x
[By the formula, cos (A – B) = cos A cos B + sin A sin B]
= cos [(n + 2) x + (n + 1) x]
= cos (4x + 2x – 4x – x)
= cos x = R.H.S.
Hence proved.
Ex 3.3 Class 11 Maths Question 11:
Prove that: \(\cos \left(\frac{3 \pi}{4}+x\right)-\cos \left(\frac{3 \pi}{4}-x\right)=-\sqrt{2} \sin x\)
Ans:

It is known that
cos A – cos B = \(-2 \sin \left(\frac{A+B}{2}\right) \cdot \sin \left(\frac{A-B}{2}\right)\)

∴ L.H.S.= \(=\cos \left(\frac{3 \pi}{4}+x\right)-\cos \left(\frac{3 \pi}{4}-x\right)\)

= \(– 2 \sin \left\{\frac{\left(\frac{3 \pi}{4}+x\right)+\left(\frac{3 \pi}{4}-x\right)}{2}\right\} \cdot \sin \left\{\frac{\left(\frac{3 \pi}{4}+x\right)-\left(\frac{3 \pi}{4}-x\right)}{2}\right\}\)

= – 2 sin (\(\frac{3 \pi}{4}\)) sin x

= – 2 sin (- \(\frac{\pi}{4}\)) sin x

= – √2 sin x = R.H.S.
Hence proved.

Ex 3.3 Class 11 Maths Question 12:
Prove that: sin ² 6x – sin ² 4x = sin 2x sin 10 x
Ans:

It is known that
sin A + sin B = 2 \(\sin \left(\frac{A-B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)

sin A – sin B = 2 \(\cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\)
L.H.S.= sin ² 6x – sin ² 4x
= (sin 6x + sin 4x) (sin 6x – sin 4x)
= (2 sin 5x cos x) (2 cos 5x sin x)
= (2 sin 5x cos 5x) (2 sin x cos x)
= sin 10x sin 2x = R.H.S.
Hence proved.

Ex 3.3 Class 11 Maths Question 13:
Prove that: cos ² 2x cos ² 6x = sin 4x sin 8x
Ans:

It is known that
cos A + cos B = 2 \(\cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)

cos A – cos = 2 \(\sin \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\)

∴ L.H.S = cos ² 2x – cos ² 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= \(\left[2 \cos \left(\frac{2 x+6 x}{2}\right) \cos \left(\frac{2 x-6 x}{2}\right)\right]\left[-2 \sin \left(\frac{2 x+6 x}{2}\right) \sin \frac{(2 x-6 x)}{2}\right]\)
∴ L.H.S.= cos ² 2x – cos ² 6x
= (cos 2x + cos 6x) (cos 2x – 6x)
= [2 cos 4x cos (-2x)] [- 2 sin 4x sin (- 2x)]
= [2 cos 4x cos 2x] [- 2 sin 4x (- sin 2x)]
= (2 sin 4x cos 4x) (2 sin 2x cos 2x)
= sin 8x sin 4x
= R.H.S.
Hence proved.

Ex 3.3 Class 11 Maths Question 14:
Prove that: sin 2x + 2 sin 4x + sin 6x = 4 cos ² x sin 4x
Ans:
L.H.S.= sin 2x + 2 sin 4x + sin 6x
= [sin 2x + sin 6x] + 2 sin 4x
= \(\left[2 \sin \left(\frac{2 x+6 x}{2}\right) \cos \left(\frac{2 x-6 x}{2}\right)\right]\) + 2 sin 4x
[∵ sin A + sin B = 2 \(\sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)]
= 2 sin 4x cos (- 2x) + 2 sin 4x
= 2 sin 4x cos 2x + 2 sin 4x
= 2 sin 4x (cos 2x + 1)
= 2 sin 4x (2 cos ² x – 1 + 1)
= 2 sin 4x (2 cos ² x)
= 4 cos ² x sin 4x
= R.H.S.
Hence proved.
Ex 3.3 Class 11 Maths Question 15:
cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)
Ans:

Ex 3.3 Class 11 Maths Question 16:
Prove that: \(\frac{\cos 9 x-\cos 5 x}{\sin 17 x-\sin 3 x}=-\frac{\sin 2 x}{\cos 10 x}\)
Ans:

Ex 3.3 Class 11 Maths Question 17:
Prove that: \(\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}\) = tan 4x
Ans:

It is known that
sin A + sin = 2 \(\sin \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)

cos A + cos = 2 \(\cos \left(\frac{A+B}{2}\right) \cos \left(\frac{A-B}{2}\right)\)

∴ L.H.S = \(\frac{\sin 5 x+\sin 3 x}{\cos 5 x+\cos 3 x}\)

= \(\frac{2 \sin \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)}{2 \cos \left(\frac{5 x+3 x}{2}\right) \cos \left(\frac{5 x-3 x}{2}\right)}\)

= \(\frac{2 \sin 4 x \cos x}{2 \cos 4 x \cos x}=\frac{\sin 4 x}{\cos 4 x}\)

= tan 4x = R.H.S.
Hence proved.

Ex 3.3 Class 11 Maths Question 18:
Prove that: \(\frac{\sin x-\sin y}{\cos x+\cos y}=\tan \frac{x-y}{2}\).
Ans:

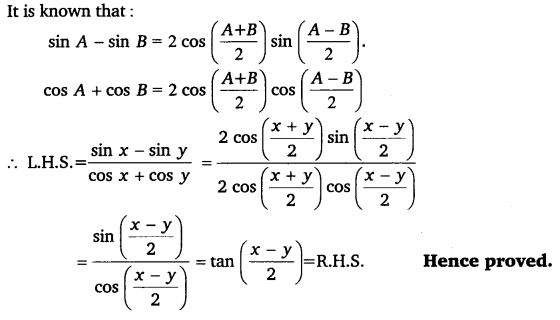
Ex 3.3 Class 11 Maths Question 19:
Prove that: \(\frac{\sin x+\sin 3 x}{\cos x+\cos 3 x}\) = tan 2x
Ans:

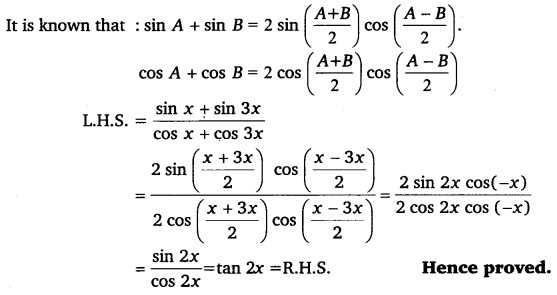
Ex 3.3 Class 11 Maths Question 20:
Prove that: \(\frac{\sin x-\sin 3 x}{\sin ^{2} x-\cos ^{2} x}\) = 2 sin x
Ans:

It is known that
sin A – sin B = 2 \(\cos \left(\frac{A+B}{2}\right) \sin \left(\frac{A-B}{2}\right)\)

cos ² A – sin ² A = cos 2A

∴ L.H.S. = \(=\frac{\sin x-\sin 3 x}{\sin ^{2} x-\cos ^{2} x}\)

= \(\frac{2 \cos \left(\frac{x+3 x}{2}\right) \sin \left(\frac{x-3 x}{2}\right)}{-\cos 2 x}\)

= \(\frac{2 \cos 2 x \sin (-x)}{-\cos 2 x}\)

= – 2 × (- sin x) = 2 sin x

= R.H.S

Hence proved.

Ex 3.3 Class 11 Maths Question 21:
Prove that: \(\frac{\cos 4 x+\cos 3 x+\cos 2 x}{\sin 4 x+\sin 3 x+\sin 2 x}\) = cot 3x
Ans:

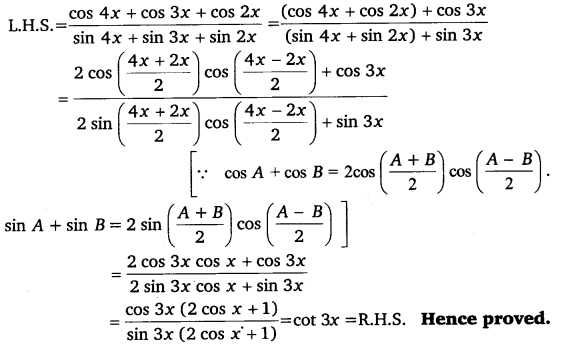
Ex 3.3 Class 11 Maths Question 22:
Prove that : cot x cot 2x – cot 2x cot 3x – cot 3x cot x = 1
Ans:
L.H.S.= cot x cot 2x – cot 2x cot 3x – cot 3x cot x
= cot x cot 2x – cot 3x (cot 2x + cot x)
= cot x cot 2x – cot (2x + x) (cot 2x + cot x)
= cot x cot 2x – \(\left[\frac{\cot 2 x \cot x-1}{\cot x+\cot 2 x}\right]\) (cot 2x + cot x)
[∵ cot (A + B) = \(\frac{\cot A \cot B-1}{\cot A+\cot B}\)]
= cot x cot 2x – (cot 2x cot x – 1)
= 1 = R.H.S.
Hence proved.
Ex 3.3 Class 11 Maths Question 23:
Prove that: tan 4x = \(\frac{4 \tan x\left(1-\tan ^{2} x\right)}{1-6 \tan ^{2} x+\tan ^{4} x}\).
Ans:
It is known that:
tan 2A = \(\frac{2 \tan A}{1-\tan ^{2} A}\)

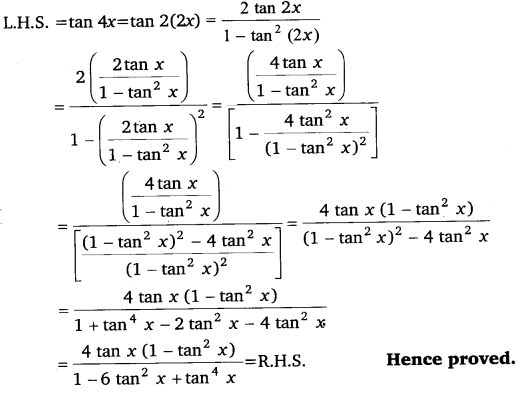
Ex 3.3 Class 11 Maths Question 24:
Prove that: cos 4x = 18 sin ² x cos ² x
Ans:
L.H.S. = cos 4x = cos 2(2x)
= 1 – 2 sin ² 2x [∵ cos 2A = 1 – 2 sin ² A]
= 1 – 2(2 sin x cos x) ² [∵ sin 2A = 2 sin A cos A]
= 1 – 8 sin ² x cos ² x
= R.H.S.
Hence proved.
Ex 3.3 Class 11 Maths Question 25:
Prove that: cos 6x = 32 cos ⁶ x – 48 cos ⁴ x + 18 cos ² x – 1
Ans:
We know that: cos 3x = 4 cos ³ x – 3cos x
On replacing x by 2x, we get
cos 3(2x) = 4 cos ³ (2x) – 3 cos 2x
⇒ cos 6x = 4 (2cos ² x – 1) ³ – 3 (2cos ² x – 1)
[∵ cos 2x = 2cos ² x – 1]
= 4 [8 cos ⁶ x – 12 cos ⁴ x + 6 cos ² x – 1] – 6 cos ² x + 3
[∵ (a – b) ³ = a ³ – 3a ² b + 3ab ² – b ³ ]
= 32 cos ⁶ x – 48 cos ⁴ x + 24 cos ² x – 4 – 6 cos ² x + 3
⇒ cos 6x = 32 cos ⁶ x – 48 cos ⁴ x + 18 cos ² x – 1
Hence proved.

त्रिकोणमितीय फलन प्रश्नावली 3.3 का हल हिंदी में

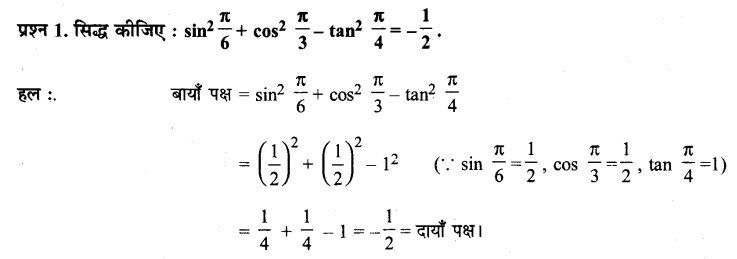
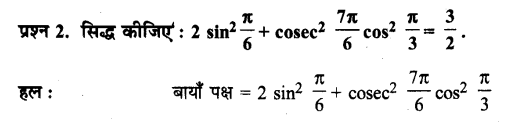
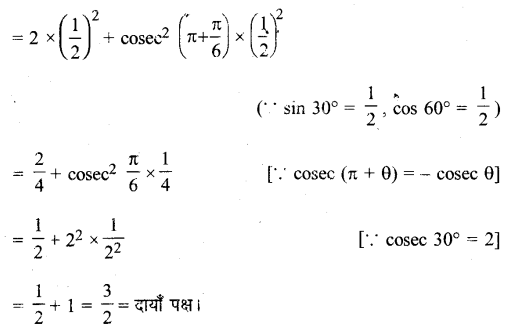
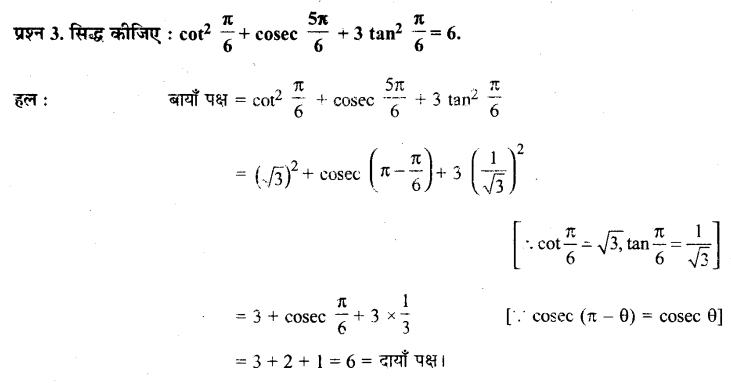
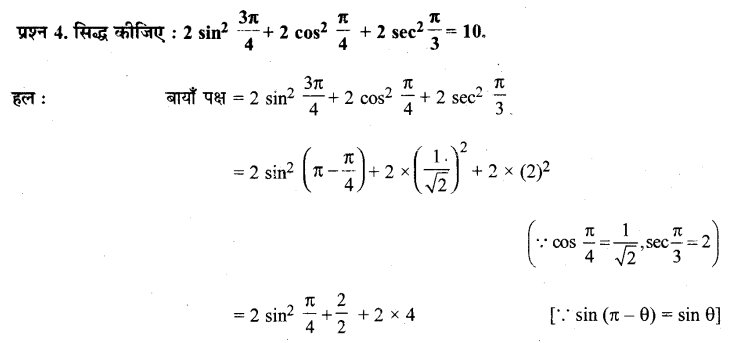
प्रश्न 5.
मान ज्ञात कीजिए:
(i) sin (75°)

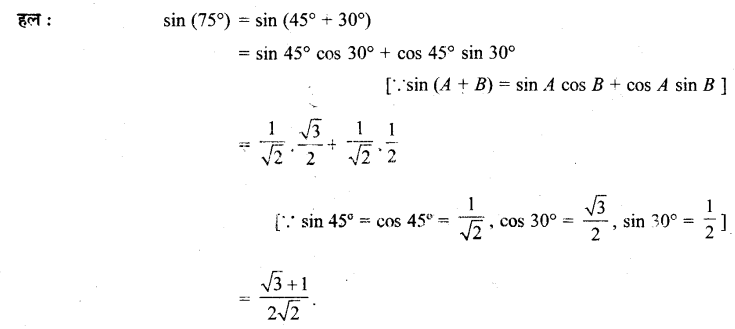
(ii) tan 15°

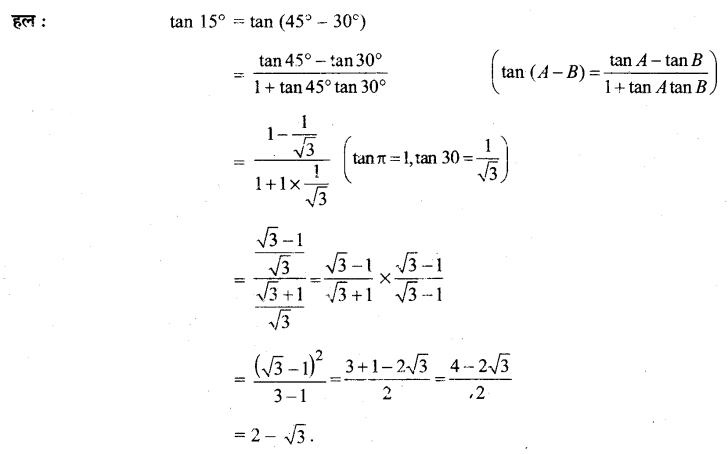
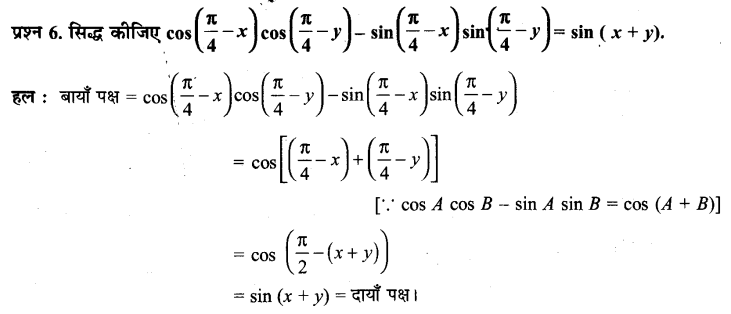
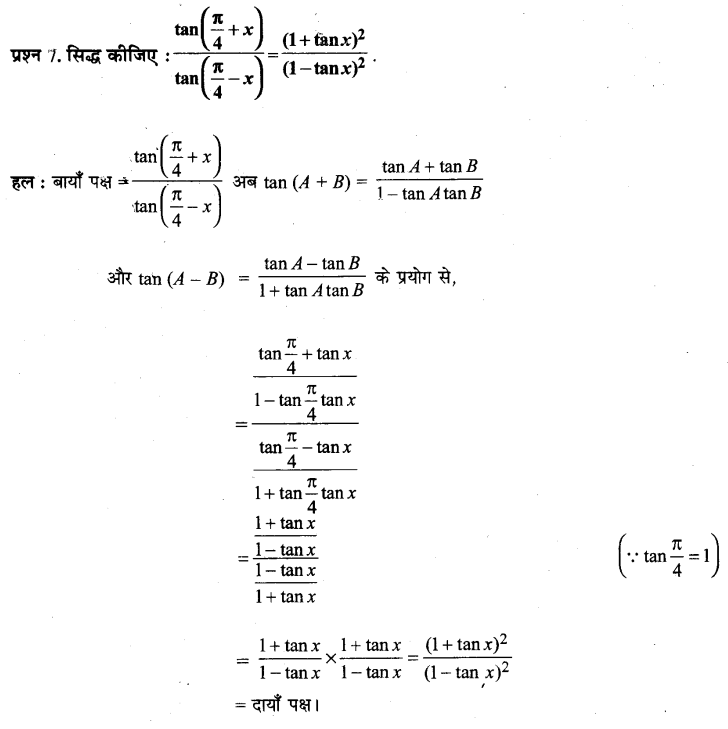
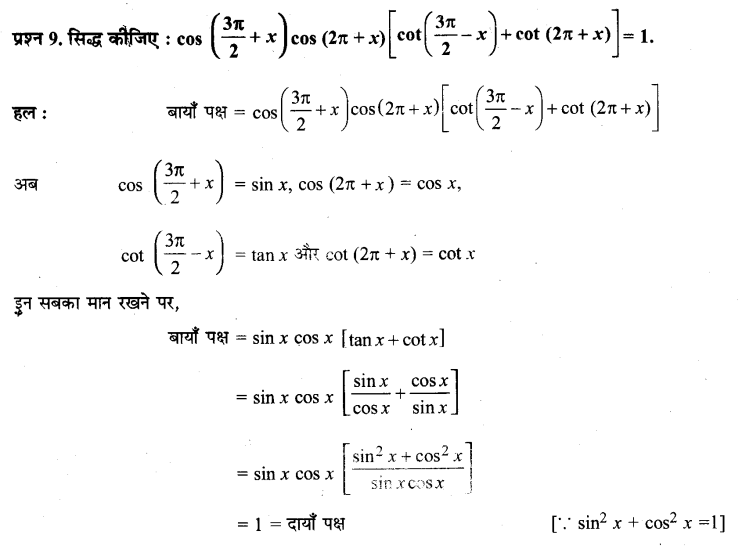
प्रश्न 10.
सिद्धि कीजिए : sin (n + 1)x sin (n + 2)x + cos (n + 1)x cos (n + 2)x = cos x.
हल :
बायां पक्ष = sin (n + 1)x sin (n + 2) x + cos (n + 1)x cos (n + 2)x
मान लीजिए (n + 2)x = A, (n + 1) x = B
= sin B sin A + cos B cos A
= cos A cos B + sin A sin B
= cos (A – B)
= cos ((n + 2) x – (n + 1) x] [A और B के मान रख कर ]
= cos (nx + 2x – nx – x)
= cos x = दाया पक्ष

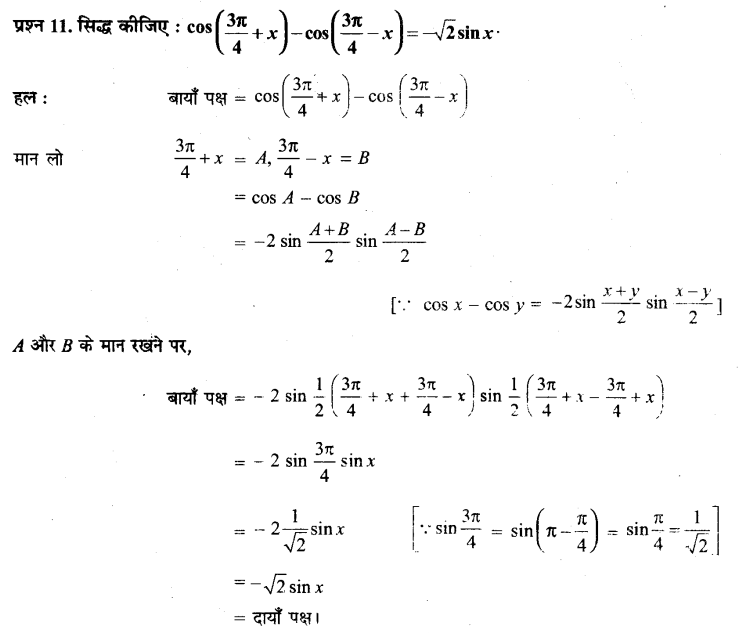
प्रश्न 12.
सिद्धि कीजिए : sin² 6x – sin² 4x = sin 2x sin 10x
हल :
बायां पक्ष = sin² 6x – sin² 4x
= sin (6x + 4x) sin (6x – 4x)
( सूत्र sin² A – sin² B = sin (A + B) sin (A – B) का प्रयोग करे]
sin 10x sin 2x
sin 2x sin 10x = दाया पक्ष

प्रश्न 13.
सिद्धि कीजिए : cos² 2x – cos² 6x = sin 4x sin 8x
हल :
बायां पक्ष = cos² 2x – cos² 6x
= 1 – sin² 2x – (1 – sin² 6x)
= sin² 6x – sin² 2x
sin² A – sin² B = sin (A + B) sin (A – B)
= sin² 6x – sin² 2x
= sin (6x + 2x) sin (6x – 2x)
= sin 8x sin 4x
= sin 4x sin 8x = दाया पक्ष

प्रश्न 14.
सिद्धि कीजिए : sin 2x + 2 sin 4x + sin 6x = 4 cos² x sin 4x
हल :
बायां पक्ष = sin 2x + 2 sin 4x + sin 6x
= (sin 2x + sin 6x) + 2 sin 4x
= 2 sin 4x cos 2x + 2 sin 4x
= 2 sin 4x (cos 2x + 1)
= 2 sin 4x (2 cos² x – 1 + 1)
= 4 sin 4x cos² x
= 4 cos² x sin 4x = दाया पक्ष

प्रश्न 15.
सिद्धि कीजिए : cot 4x (sin 5x + sin 3x) = cot x (sin 5x – sin 3x)

AI CONTENT END 1 <rdf:RDF xmlns:rdf="http://www.w3.org/1999/02/22-rdf-syntax-ns#" xmlns:dc="http://purl.org/dc/elements/1.1/" xmlns:trackback="http://madskills.com/public/xml/rss/module/trackback/"> <rdf:Description rdf:about="https://www.LearnCBSE.online/ncert-solutions-for-class-11-maths-chapter-3-ex-3-3/" dc:identifier="https://www.LearnCBSE.online/ncert-solutions-for-class-11-maths-chapter-3-ex-3-3/" dc:title="NCERT Solutions for Class 11 Maths Chapter 3 Ex 3.3" trackback:ping="https://www.LearnCBSE.online/ncert-solutions-for-class-11-maths-chapter-3-ex-3-3/trackback/" /> </rdf:RDF>