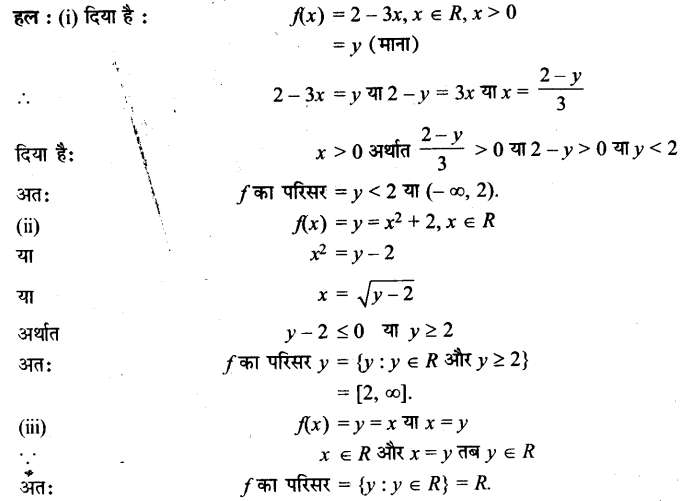Get Free NCERT Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3 PDF in Hindi and English Medium. Relations and Functions Class 11 Maths NCERT Solutions are extremely helpful while doing your homework. Relations and Functions Exercise 2.3 Class 11 Maths NCERT Solutions were prepared by Experienced LearnCBSE.online Teachers. Detailed answers of all the questions in Chapter 2 Class 11 Relations and Functions Ex 2.3 provided in NCERT Textbook.
- Relations and Functions Class 11 Ex 2.1
- Relations and Functions Class 11 Ex 2.2
- Relations and Functions Class 11 Ex 2.3
- Relations and Functions Class 11 Miscellaneous Exercise
- संबंध एवं फलन प्रश्नावली 2.1 का हल हिंदी में
- संबंध एवं फलन प्रश्नावली 2.2 का हल हिंदी में
- संबंध एवं फलन प्रश्नावली 2.3 का हल हिंदी में
- संबंध एवं फलन विविध प्रश्नावली का हल हिंदी में
- NCERT Exemplar Class 11 Maths Chapter 2 Relations and Functions
- Relations and Functions Class 11 Notes
- Relations and Functions Formulas
- RD Sharma Class 11 Solutions Chapter 2 Relations
Free download NCERT Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3 PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, BIE, Intermediate and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.
NCERT Solutions for Class 11 Maths Chapter 2 Ex 2.3

Question-1
Which of the following relations are functions? Give reasons. If it is a function, determine its domain and range.
(i) {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) (1, 3), (1, 5), (2, 5)}
Ans.
(i) {(2, 1), (5,1), (8, 1), (11, 1), (14, 1), (17,1)}
Since 2, 5, 8, 11, 14, and 17 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain={2, 5, 8, 11, 14, 17} and range={l}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
Since 2, 4, 6, 8, 10, 12, and 14 are the elements of the domain of the given relation having their unique images, this relation is a function.
Here, domain = {2, 4, 6, 8, 10, 12, 14} and range = {1, 2, 3, 4, 5, 6, 7}
(iii) {(1, 3), (1, 5), (2, 5)}
Since the same first element i.e., 1 corresponds to two different images i.e.,3 and 5, this relation is not a function.
Question-2
Find the domain and range of the following real functions:
(i) f(x) = – |x|
(ii) f(x) =
![]()
Ans.
(i) f(x) = – |x|, f(x) ≤ 0, ∀ x ∈ R
Domain of f = R
Range of f = {y ∈ R, y < 0}
(ii) f(x) =
![]()
All, f is not defined for 9 – x
2
≤ 0 or x
2
≤ 9 or when x ≥ 3 or x ≤ – 3.
Also, for each real number x lying between – 3 and 3 or for x = – 3, 3 f(x) is unique.
∴ Domain (f) = {x : x ∈ R and – 3 < x < 3}
Further, y =
![]() or y
2
= 9 – x
2
or y
2
= 9 – x
2
or x =
![]()
Again, x is not defined for
9 – y
2
< 0 or y
2
> 9 or y > 3 or y < – 3.
But y cannot be – ve
∴ Range (f) = {y : y ∈ R and 0 < y < 3}
Question-3
A function fis defined by f(x) = 2x – 5. Write down the values of
(i) f(0)
(ii) f(7)
(iii) f(- 3)
Ans.
The given function is f(x) = 2x – 5. Therefore,
(i) f(0) = 2 × 0 – 5 = 0 – 5 = – 5
(ii) f(7) = 2 × 7 – 5 = 14 – 5 = 9
(iii) f(- 3) = 2 × (- 3) – 5 = – 6 – 5 = -11.
Question-4
The function ‘t’ which maps temperature in degree Celsius into temperature in degree Fahrenheit is defined by t(C) = \(\frac{9 C}{5}\) + 32. Find
(i) f(0)
(ii) t(28)
(iii) t(- 10)
(iv) The value of C, when t(C) = 212.
Ans.
The given function is t (C) = \(\frac{9 C}{5}\) + 32. Therefore,
(i) t(0) = \(\frac{9 \times 0}{5}\) + 32 = 0 + 32 = 32
(ii) t(28) = \(\frac{9 \times 28}{5}\) + 32 = \(\frac{252+160}{5}\) = \(\frac{412}{5}\)
(iii) t (- 10) = \(\frac{9 \times(-10)}{5}\) + 32 = 9 × ( – 2) + 32
(iv) It is given that t(C) = 212
∴ 212 = \(\frac{9 C}{5}\) + 32 \(\frac{9 C}{5}\)
= 212 – 32 \(\frac{9 C}{5}\) = 180
9C = 180 × 5 C = \(\frac{180 \times 5}{9}\) = 100.
Thus, the value of t, when t(C) = 212, is 100.
Question-5
Find the range of each of the following functions :
(i) f(x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x
2
+ 2, x is a real number.
(iii) f(x) = x, x is a real number.
Ans.
(i) Let f(x) = y = 2 – 3x is x = \(\frac{2-y}{3}\)
Now x > 0 is 2 – y > 0 or y < 2
Range (f) = {y : y ∈ R and y < 2}
(ii) Let f(x) = y = x
2
+ 2 is x
2
= y – 2 or x =
![]() ⇒ y > 2
⇒ y > 2
Range (f) = {y : y ∈ R and y > 2}
(iii) f(x) = x, x is a real number
x = f(x) = y = a real number
Range (f) = {y : y ∈ R}
NCERT Solutions for Class 11 Maths Chapter 2 Relations and Functions Ex 2.3
प्रश्न 1.
निम्नलिखित संबंधों में से कौन से फलन हैं ? कारण का उल्लेख कीजिए। यदि संबंध एक फलन है तो उसका परिसर निर्धारित कीजिए।
(i) {(2,1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
(ii) {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
(iii) {(1, 3), (1, 5), (2, 5)}
हल:
(i) माना R = {(2, 1), (5, 1), (8, 1), (11, 1), (14, 1), (17, 1)}
यह संबंध एक फलन है क्योंकि किसी भी दो क्रमित युग्म का पहला घटक बराबर नहीं है।
प्रान्त = {2, 6, 8, 11, 14, 17} तथा परिसर = {1}.
(ii) माना R = {(2, 1), (4, 2), (6, 3), (8, 4), (10, 5), (12, 6), (14, 7)}
यह एक फलन है क्योंकि किसी भी दो क्रमित युग्म का पहला घटक बराबर नहीं है।
अतः प्रांत = {2, 4, 6, 8, 10, 12, 14}, परिसर = {1, 2, 3, 4, 5, 6, 7}.
(iii) यह एक फलन नहीं है क्योंकि (1, 3), (1, 5) में पहला घटक समान है।

प्रश्न 4.
फलन ‘t’ सेल्सियस तापमान का फारेनहाइट तापमान में प्रतिचित्रण करता है, जो t(C) = \(\frac { 9C }{ 5 }\) + 32 द्वारा परिभाषित है। निम्नलिखित को ज्ञात कीजिए:
(i) t(0)
(ii) t(28)
(iii) t(-10)
(iv) C का मान, जब t(C) = 212
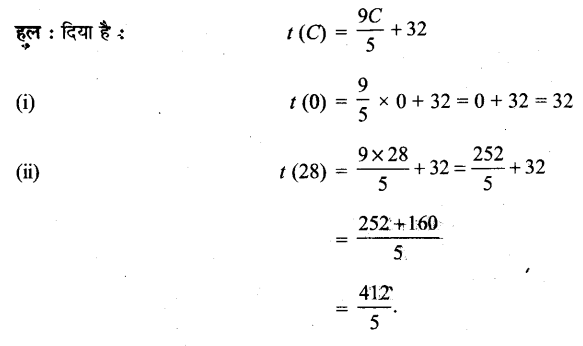
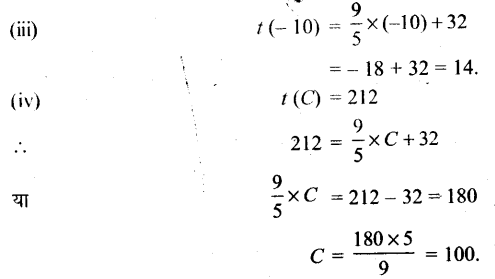
प्रश्न 5.
निम्नलिखित में से प्रत्येक फलन का परिसर ज्ञात कीजिए:
(i) f(x) = 2 – 3x, x ∈ R, x > 0.
(ii) f(x) = x² + 2, x एक वास्तविक संख्या है।
(iii) f(x) = x, एक वास्तविक संख्या है।