NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.4

Get Free NCERT Solutions for Class 10 Maths Chapter 6 Ex 6.4 PDF. Triangles Class 10 Maths NCERT Solutions are extremely helpful while doing your homework. Exercise 6.4 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.in Teachers. Detailed answers of all the questions in Chapter 6 Maths Class 10 Triangles Exercise 6.4 provided in NCERT TextBook.

You can also download NCERT Solutions For Class 10 Maths to help you to revise complete syllabus and score more marks in your examinations.

Free download NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.4 Triangles PDF in Hindi Medium as well as in English Medium for CBSE, Uttarakhand, Bihar, MP Board, Gujarat Board, AP SSC, TS SSC and UP Board students, who are using NCERT Books based on updated CBSE Syllabus for the session 2019-20.

• Triangles Class 10 Mind Map
• Triangles Class 10 Ex 6.1
• Triangles Class 10 Ex 6.1 in Hindi Medium
• Triangles Class 10 Ex 6.2
• Triangles Class 10 Ex 6.2 in Hindi Medium
• Triangles Class 10 Ex 6.3
• Triangles Class 10 Ex 6.3 in Hindi Medium
• Triangles Class 10 Ex 6.4
• Triangles Class 10 Ex 6.4 in Hindi Medium
• Triangles Class 10 Ex 6.5
• Triangles Class 10 Ex 6.5 in Hindi Medium
• Triangles Class 10 Ex 6.6
• Triangles Class 10 Ex 6.6 in Hindi Medium
• Extra Questions for Class 10 Maths Triangles
• Triangles Class 10 Notes Maths Chapter 6
• NCERT Exemplar Class 10 Maths Chapter 6 Triangles
• Important Questions for Class 10 Maths Chapter 6 Triangles

You can also download the free PDF of Ex 6.4 Class 10 Triangles NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 6
Chapter Name	Triangles
Exercise	Ex 6.4
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions For Class 10 Maths Chapter 6 Triangles Ex 6.4

NCERT Solutions for Class 10 Maths Chapter 6 Triangles Ex Ex 6.4 are part of NCERT Class 10 Maths Solutions . Here we have given NCERT Solutions for Class 10 Maths Chapter 6 Triangles Exercise 6.4

Question 1.
Let ∆ABC ~ ∆DEF and their areas be, respectively, 64 cm ² and 121 cm ² . If EF = 15.4 cm, find BC.
Solution:

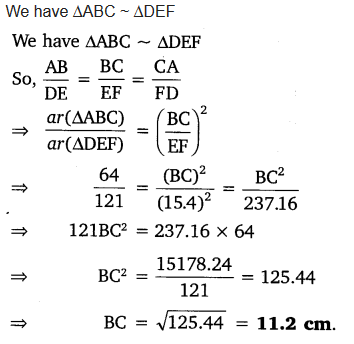
Question 2.
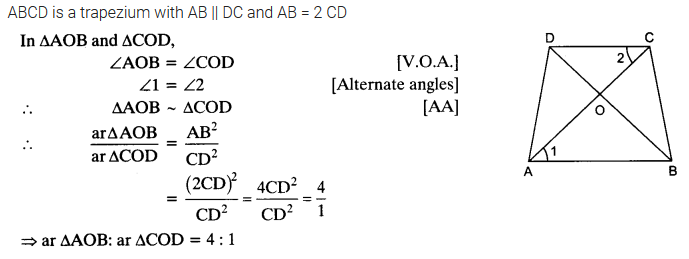
Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Solution:

Download NCERT Solutions For Class 10 Maths Chapter 6 Triangles PDF

Question 3.
In the given figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that: \(\frac { ar\left( ABC \right) }{ ar\left( DBC \right) } =\frac { AO }{ DO } \)
Solution:

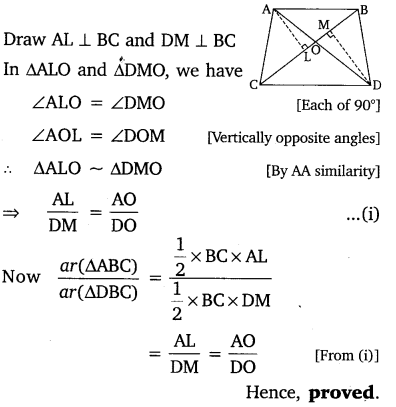
Question 4.
If the areas of two similar triangles are equal, prove that they are congruent.
Solution:

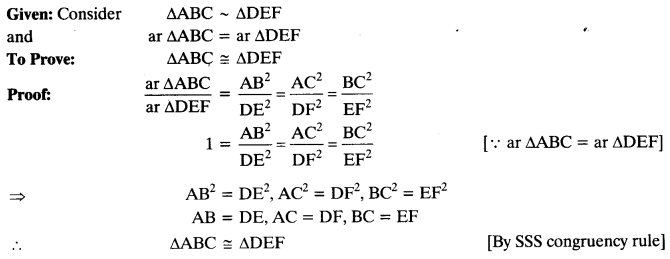
Question 5.
D, E and F are respectively the mid-points of sides AB, BC and CA of ∆ABC. Find the ratio of the areas of ∆DEF and ∆ABC.
Solution:

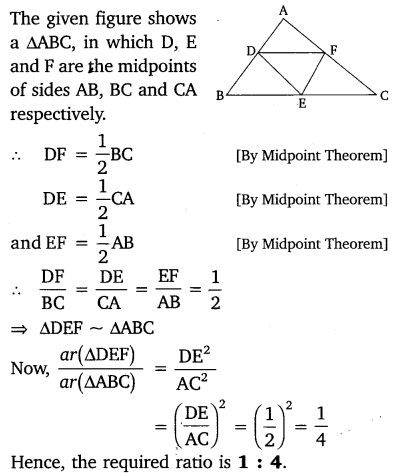
Question 6.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:

Question 7.
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:

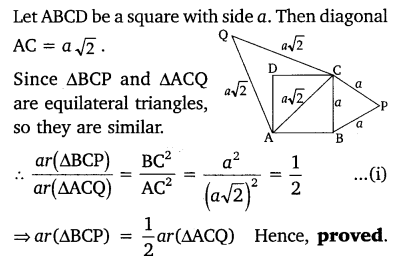
Question 8.
Tick the correct answer and justify
(i) ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(a) 2 :1
(b) 1:2
(c) 4 :1
(d) 1:4

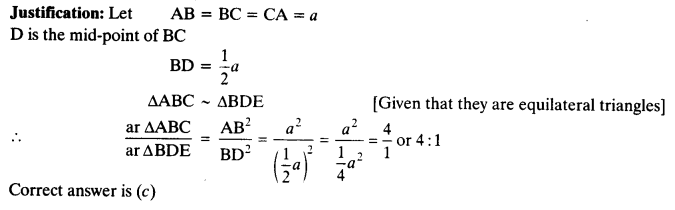
(ii) Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3
(b) 4 : 9
(c) 81 : 16
(d) 16 : 81

NCERT Solutions for Class 10 Maths Chapter 6 Triangles in Hindi Medium Ex 6.4 (NCERT Book Page No – 158)

एनसीईआरटी समाधान कक्षा 10 गणित त्रिभुज प्रश्नावली 6.4 का हल हिंदी में

प्र० 1. मान लीजिए ΔABC ~ ΔDEF और इनके क्षेत्रफल क्रमशः 64 cm2 और 121 cm ² हैं| यदि EF = 15.4 cm ² हो, तो BC ज्ञात कीजिए |
हलः हमें प्राप्त है।
ar(ΔABC) = 64 cm ²

प्र० 2. एक समलंब ABCD जिसमें AB || DC हैं, के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं| यदि AB = 2 CD हो तो ΔAOB और ΔCOD के क्षेत्रफलों का अनुपात ज्ञात कीजिए|
हलः हमें प्राप्त है: समलंब ABCD में, AB | DC
विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।
ΔAOB और ΔCOD में,
∠AOB = ∠COD [शीर्षभिमुख कोण]
∠OAB = ∠OCD [एकान्तर कोण]

प्र० 3. आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं| यदि AD, BC कोप O पर प्रतिच्छेद करे, तो दर्शाइए की

प्र० 4.यदि दो समरूप तत्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वान्गसम होते हैं|

प्र० 5. एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिन्दु क्रमशः D, E और F हैं| त्रिभुज DEF और त्रिभुज ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए|
हलः हमें प्राप्त है: ΔABC में भुजाओं AB, AC और BC
के मध्य बिन्दु क्रमशः D, E और F हैं।
D, F और F को मिलाने पर ΔDEF बनता है
अब, D भुजा AB का मध्य बिंदु है।

प्र० 6. सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है|
हलः हमें प्राप्त है: ΔABC और ΔDEF इस प्रकार है कि ΔABC ~ ΔDEF
तथा AM और DN क्रमशः भुजाओं BC और EF’ के संगत माध्यिकाएँ हैं।
चूंकि ΔABC ~ ΔDEF
इनके क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के वर्गों के अनुपात के समान होगी।

प्र० 7. सिद्ध कीजिए कि दो एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है |
हलः हमें प्राप्त है कि वर्ग ABCD में विकर्ण AC है।
भुजा BC पर समबाहु ΔBQC और विकर्ण AC पर समबाहु ΔAPC बनाई गई है।
सभी समबाहु त्रिभुजें समरूप होती हैं।

प्र० 8. ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कोई भुजद BC का मध्य-बिन्दु है| त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है:
(A) 2 : 1
(B) 1 : 2
(C) 4 : 1
(D) 1 : 4
हलः हमें प्राप्त है।
समबाहु ΔABC में, भुजा BC का मध्यबिंदु D है। DE को इस प्रकार खींचा गया है कि ΔBDE भी एक समबाहु त्रिभुज है।

चूंकि सभी समबाहु त्रिभुजें समरूप होती हैं।
ΔABC ~ ΔBDE
इनके क्षेत्रफलों का अनुपात इनकी संगत भुजाओं के वर्गों के अनुपात के समान होता है।

प्र० 9. दो समरूप त्रिभुजों की भुजाएँ 4 : 9 के अनुपात में हैं| इन त्रिभुजों के क्षेत्रफलों का अनुपात है :
(A) 2 : 3
(B) 4 : 9
(C) 81 : 16
(D) 16 : 81
हलः हमें दो समरूप त्रिभुजें इस प्रकार प्राप्त हैं कि उनकी संगत भुजाओं का अनुपात 4:9 है।
चूंकि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के वर्गों के समान होता है।

LearnCBSE Online