Get Free NCERT Solutions for Class 10 Maths Chapter 11 Ex 11.1 PDF. Constructions Class 10 Maths NCERT Solutions are extremely helpful while doing your homework. Exercise 11.1 Class 10 Maths NCERT Solutions were prepared by Experienced LearnCBSE.online Teachers. Detailed answers of all the questions in Chapter 11 Maths Class 10 Constructions Exercise 11.1 provided in NCERT TextBook.
Topics and Sub Topics in Class 10 Maths Chapter 11 Constructions:
| Section Name | Topic Name |
| 11 | Constructions |
| 11.1 | Introduction |
| 11.2 | Division Of A Line Segment |
| 11.3 | Construction Of Tangents To A Circle |
| 11.4 | Summary |
- Constructions Class 10 Ex 11.1
- प्रश्नावली 11.1 का हल हिंदी में
- Constructions Class 10 Ex 11.2
- प्रश्नावली 11.2 का हल हिंदी में
- Extra Questions for Class 10 Maths Constructions
NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1
NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1 are part of NCERT Solutions for Class 10 Maths . Here we have given NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.1
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 10 |
| Subject | Maths |
| Chapter | Chapter 11 |
| Chapter Name | Constructions |
| Exercise | Ex 11.1 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
Ex 11.1 Class 10 Maths Question 1.
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Solution:
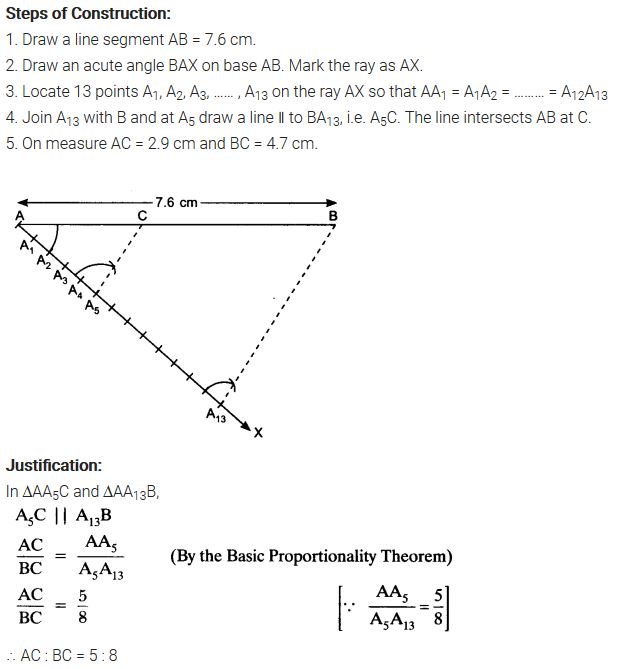
Ex 11.1 Class 10 Maths Question 2.
Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac { 2 }{ 3 }\) of the corresponding sides of the first triangle.
Solution:
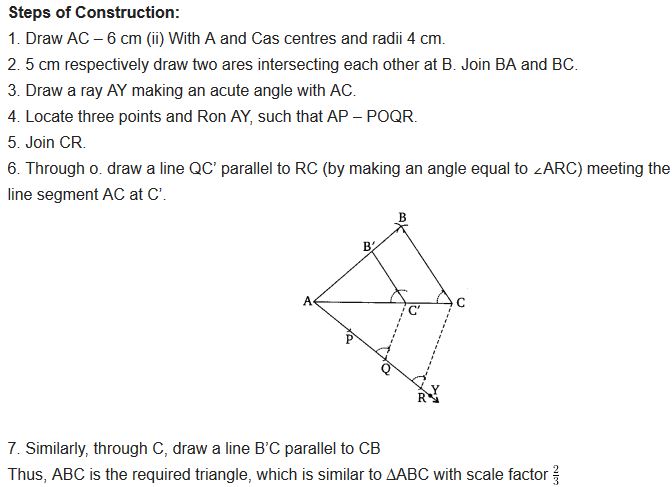

You can also download the free PDF of Ex 11.1 Class 10 Constructions NCERT Solutions or save the solution images and take the print out to keep it handy for your exam preparation.
Download NCERT Solutions For Class 10 Maths Chapter 11 Constructions PDF
Ex 11.1 Class 10 Maths Question 3.
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are \(\frac { 7 }{ 5 }\) of the corresponding sides of the first triangle.
Solution:
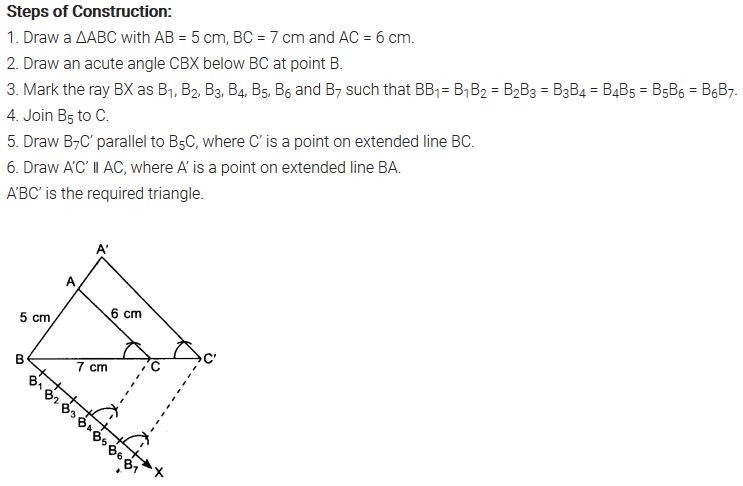

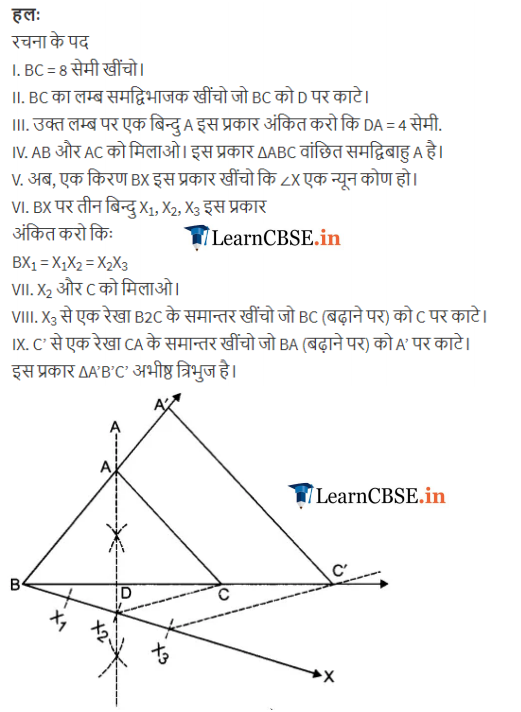
Ex 11.1 Class 10 Maths Question 4.
Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 1\(\frac { 1 }{ 2 }\) times the corresponding sides of the isosceles triangle.
Solution:
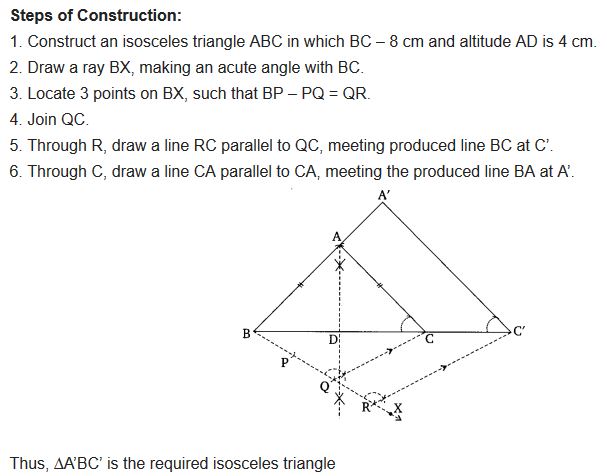

Ex 11.1 Class 10 Maths Question 5.
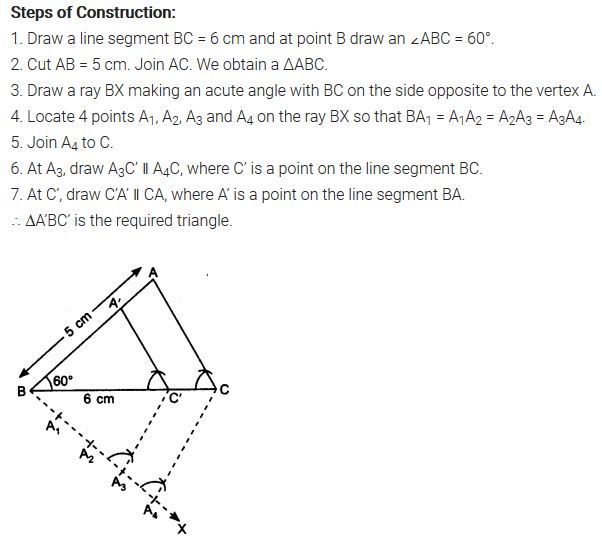
Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac { 3 }{ 4 }\) of the corresponding sides of the triangle ABC.
Solution:

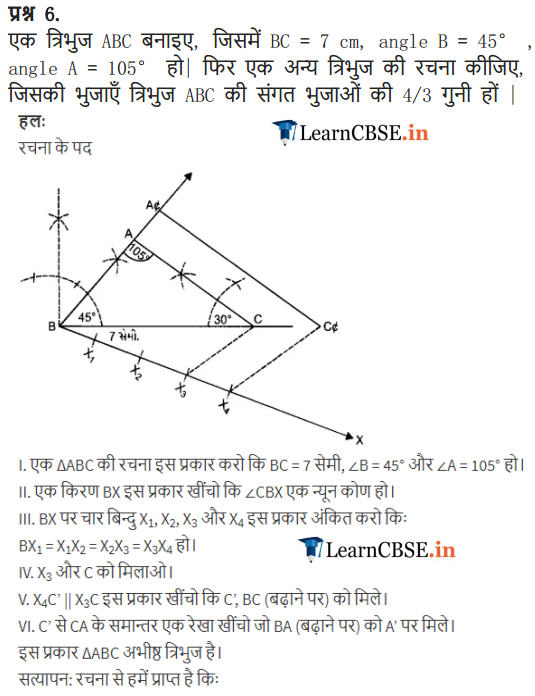
Ex 11.1 Class 10 Maths Question 6.
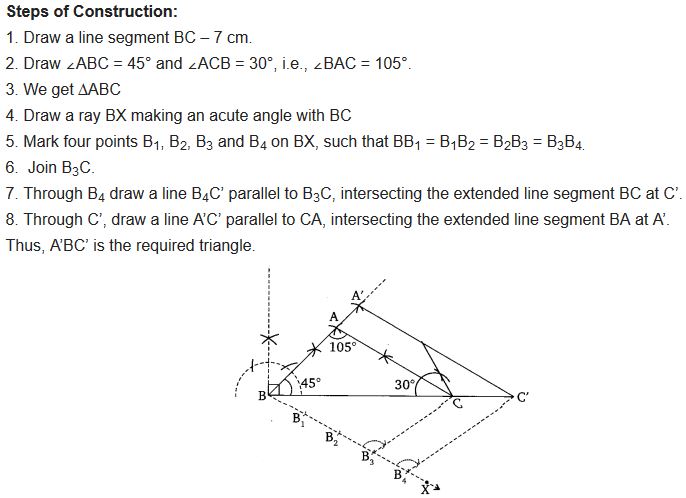
Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac { 4 }{ 3 }\) times the corresponding sides of ∆ABC.
Solution:

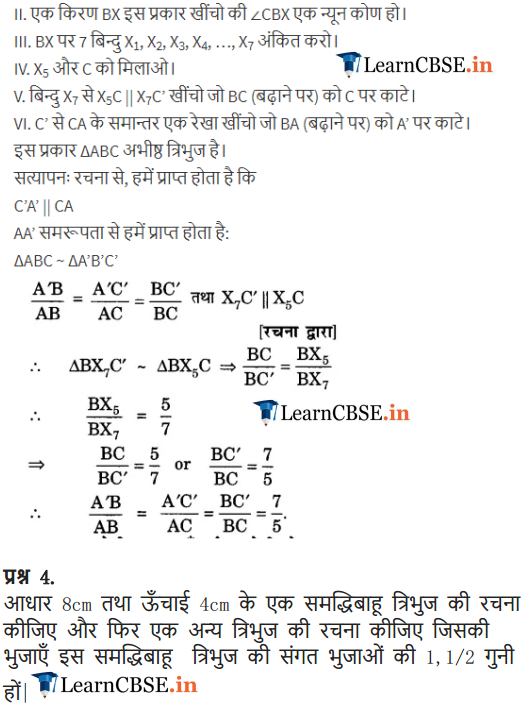
Ex 11.1 Class 10 Maths Question 7.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac { 5 }{ 3F }\) times the corresponding sides of the given triangle.
Solution:
Steps of Construction:
1. Construct a ∆ABC, such that BC = 4 cm,
CA = 3 cm and ∠BCA = 90°
2. Draw a ray BX making an acute angle
with BC.
3. Mark five points B
1
, B
2
, B
3
, B
4
and B
5
on BX,
such that BB
1
= B
1
B
2
= B
2
B
3
= B
3
B
4
= B
4
B
5.
4. Join B
3
C.
5. Through B
5
, draw B
5
C’ parallel to B
3
C
intersecting BC produced at C’.
6. Through C’, draw C’A’ parallel to CA
intersecting AB produced at A’.
Thus, ∆A’BC’ is the required right triangle.
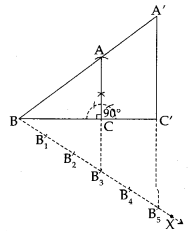
Justification:

Class 10 Maths Constructions Mind Maps
Construction
Construction implies drawing geometrical figures accurately such that triangles, quadrilateral and circles with the help of ruler and compass.
Division of a Line Segment
A line segment can be divided in a given ratio (both internally and externally)
Example:
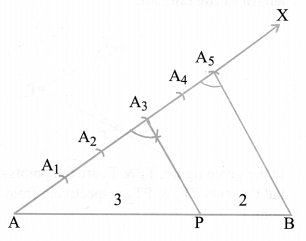
Divide a line segment of length 12 cm internally in the ratio 3:2.
Solution :
Steps of construction :
(i) Draw a line segment AB = 12 cm. by using a ruler.
(ii) Draw a ray making a suitable acute angle ∠BAX with AB.
(iii) Along AX, draw 5 ( = 3 + 2) arcs intersecting the ray AX at A
1
? A
2
, A
3
, A
4
and A
5
such that
AA
1
= A
1
A
2
= A
2
A
3
= A
3
A
4
= A
4
A
5
(iv) Join BA
5
.
(v) Through A
3
draw a line A
3
P parallel to A
5
B making ∠AA
3
P = ∠AA
5
B, intersecting AB at point P.
The point P so obtained is the required point, which divides AB internally in the ratio 3 : 2.
Similar Triangles
(i) This Construction involves two different situation.
(a) Construction of a similar triangle smaller than the given triangle.
(b) Construction of a similar triangle greater than the given triangle.
(ii) The ratio of sides of the triangle to be constructed with the corresponding sides of the given triangle is called scale factor.
Example:
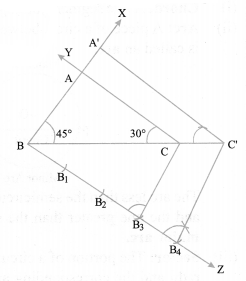
Draw a triangle ABC with side BC = 7 cm. ∠B = 45°, ∠A = 105°. Construct a triangle whose sides are (4/3) times the corresponding side of ∆ABC.
Solution :
Steps of construction :
(i) Draw BC = 7 cm.
(ii) Draw a ray BX and CY such that ∠CBX= 45° and
∠BCY = 180° – (45° + 105°) = 30°
Suppose BX and CY intersect each other at A.
∆ABC so obtained is the given triangle.
(iii) Draw a ray BZ making a suitable acute angle with BC on opposite side of vertex A with respect to BC.
(iv) Draw four (greater of 4 and 3 in 4/3) arcs intersecting the ray BZ at B
1
, B
2
, B
3
, B
4
such that BB
1
= B
1
B
2
= B
2
B
3
= B
3
B
4
.
(v) Join B
3
to C and draw a line through B
4
parallel to B
3
C, intersecting the extended line segment BC at C’.
(vi) Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’. Triangle A’BC’ so obtained is the required triangle.
Tangents to a Circle
Two tangents can be drawn to a given circle from a point outside it.
Example:
Draw a circle of radius 4 cm. Take a point P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.
Solution :
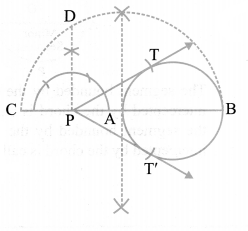
Steps of construction :
(i) Draw a circle of radius 4 cm.
(ii) Take a point P outside the circle and draw a secant PAB, intersecting the circle at A and B.
(iii) Produce AP to C such that AP = CP.
(iv) Draw a semi-circle with CB as diameter.
(v) Draw PD ⊥ CB, intersecting the semi-circle at D.
(vi) With P as centre and PD as radius draw arcs to intersect the given circle at T and T’
(vii) Join PT and PT’. Then, PT and PT’ are the required tangents.
Note:
If centre of a circle is not given, then it can be located by finding point of intersection of perpendicular bisector, of any two nonparallel chords of a circle.
NCERT Solutions for Class 10 Maths Chapter 11 Constructions (Hindi Medium) Ex 11.1
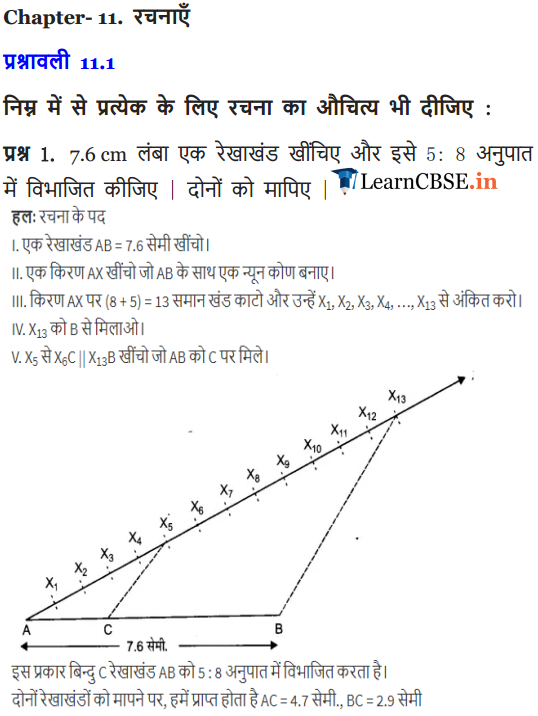


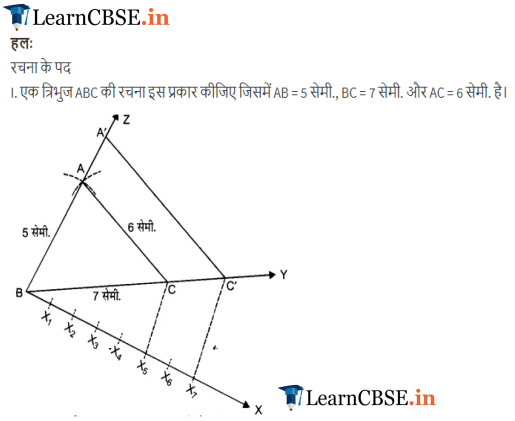





NCERT Solutions for Class 10 Maths
- Chapter 1 Real Numbers
- Chapter 2 Polynomials
- Chapter 3 Pair of Linear Equations in Two Variables
- Chapter 4 Quadratic Equations
- Chapter 5 Arithmetic Progressions
- Chapter 6 Triangles
- Chapter 7 Coordinate Geometry
- Chapter 8 Introduction to Trigonometry
- Chapter 9 Some Applications of Trigonometry
- Chapter 10 Circles
- Chapter 11 Constructions
- Chapter 12 Areas Related to Circles
- Chapter 13 Surface Areas and Volumes
- Chapter 14 Statistics
- Chapter 15 Probability