NCERT Exemplar Class 11 Maths Chapter 8 Binomial Theorem are part of NCERT Exemplar Class 11 Maths . Here we have given NCERT Exemplar Class 11 Maths Chapter 8 Binomial Theorem.
NCERT Exemplar Class 11 Maths Chapter 8 Binomial Theorem
Short Answer Type Questions:
Q1. Find the term independent of x, where x≠0, in the expansion of \({ \left( \frac { 3{ x }^{ 2 } }{ 2 } -\quad \frac { 1 }{ 3x } \right) }^{ 15 }\)

Q2. If the term free from x is the expansion of \({ \left( \sqrt { x } -\frac { k }{ { x }^{ 2 } } \right) }^{ 10 }\) is 405, then find the value of k.
Sol: Given expansion is \({ \left( \sqrt { x } -\frac { k }{ { x }^{ 2 } } \right) }^{ 10 }\)
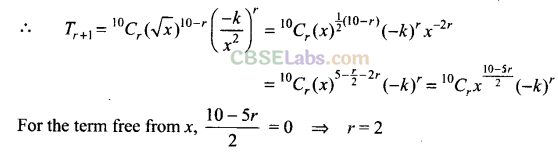
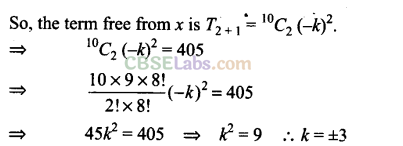
Q3. Find the coefficient of x in the expansion of (1 – 3x + 1x 2 )( 1 -x) 16 .
Sol: (1 – 3x + 1x 2 )( 1 -x) 16
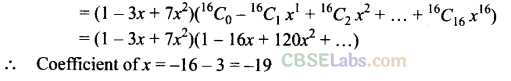
Q4. Find the term independent of x in the expansion of \({ \left( 3x-\frac { 2 }{ { x }^{ 2 } } \right) }^{ 15 }\)
Sol: Given Expression \({ \left( 3x-\frac { 2 }{ { x }^{ 2 } } \right) }^{ 15 }\)

Q5. Find the middle term (terms) in the expansion of


Q6. Find the coefficient of x 15 in the expansion of \({ \left( x-{ x }^{ 2 }\quad \right) }^{ 10 }\)
Sol: Given expression is \({ \left( x-{ x }^{ 2 }\quad \right) }^{ 10 }\)
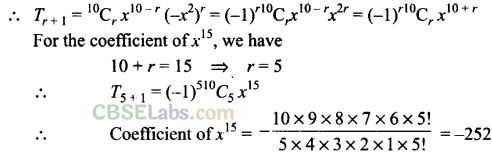
Q7. Find the coefficient of \(\frac { 1 }{ { x }^{ 17 } } \) in the expansion of \({ \left( { x }^{ 4 }-\frac { 1 }{ { x }^{ 3 } } \quad \right) }^{ 15 } \)

Q8. Find the sixth term of the expansion (y 1/2 + x 1/3 ) n , if the binomial coefficient of the third term from the end is 45.
>
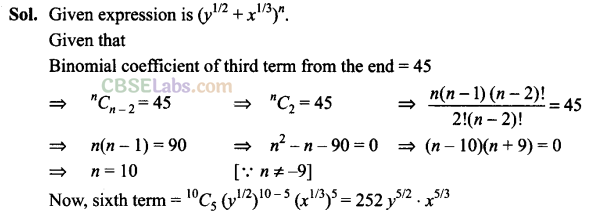
Q9. Find the value of r, if the coefficients of (2r + 4)th and (r – 2)th terms in the expansion of (1 + x) 18 are equal.

Q10. If the coefficient of second, third and fourth terms in the expansion of (1 + x) 2 ” are in A.P., then show that 2n 2 – 9n + 7 = 0.

Q11. Find the coefficient of x 4 in the expansion of (1 + x + x 2 + x 3 ) 11 .
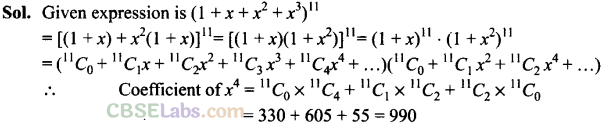
Long Answer Type Questions
Q12. If p is a real number and the middle term in the expansion \({ \left( \frac { p }{ 2 } +2\quad \right) }^{ 8 } \) is 1120, then find the value of p.
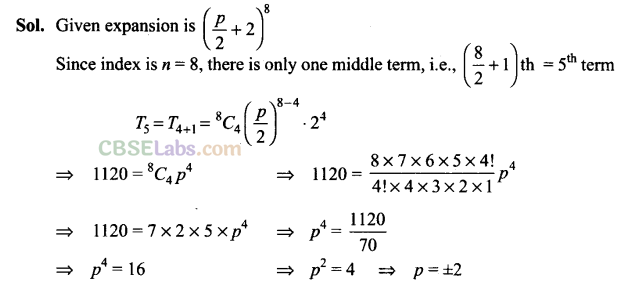


Q15. In the expansion of (x + a) n , if the sum of odd term is denoted by 0 and the sum of even term by Then, prove that

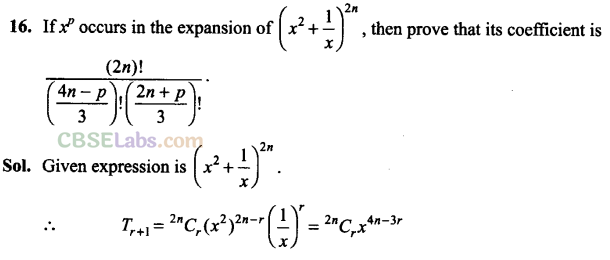
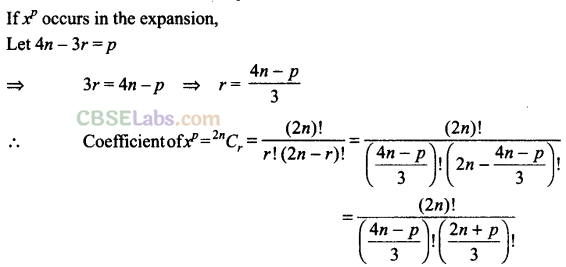
Q17. Find the term independent ofx in the expansion of (1 +x + 2x
3
)\({ \left( \frac { 3 }{ 2 } { x }^{ 2 }-\frac { 1 }{ 3x } \quad \quad \right) }^{ 9 } \)

Objective Type Questions
Q18. The total number of terms in the expansion of (x + a) 100 + (x – a) 100 after simplification is
(a) 50
(b) 202
(c) 51
(d) none of these
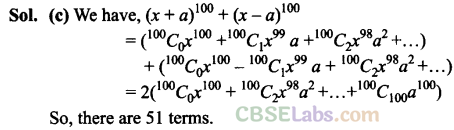
Q19. If the integers r > 1, n > 2 and coefficients of (3r)th and (r + 2)nd terms in the binomial expansion of (1 + x)
2n
are equal, then
(a) n = 2r
(b) n = 3r
(c) n = 2r + 1
(d) none of these
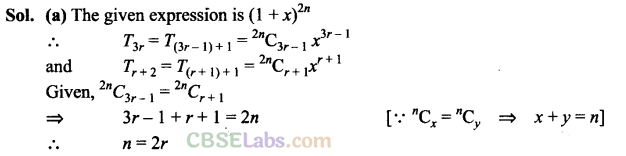
Q20. The two successive terms in the expansion of (1 + x)
24
whose coefficients are in the ratio 1 : 4 are
(a) 3
rd
and 4
th
(b) 4
th
and 5
th
(c) 5
th
and 6
th
(d) 6
th
and 7
th

Q21. The coefficients of x
n
in the expansion of (1 + x)
2n
and (1 + x)
2n
~
1
are in the ratio
(a) 1 : 2
(b) 1 : 3
(c) 3 : 1
(d) 2:1

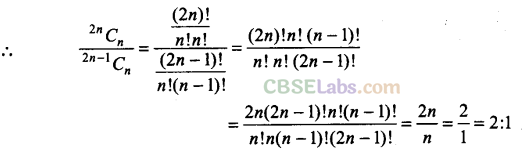
Q22. If the coefficients of 2
nd
, 3
rd
and the 4
th
terms in the expansion of (1 + x)
n
are in A.P., then the value of n is
(a) 2
(b) 7
(c) 11
(d) 14

Q23. If A and B are coefficients of x n in the expansions of (1 + x) 2n and (1 + x) 2n – 1 respectively, then A/B equals to
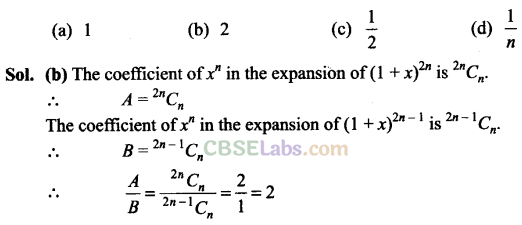



NCERT Exemplar Class 11 Maths Solutions
- Chapter 1 Sets
- Chapter 2 Relations and Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Principle of Mathematical Induction
- Chapter 5 Complex Numbers and Quadratic Equations
- Chapter 6 Linear Inequalities
- Chapter 7 Permutations and Combinations
- Chapter 8 Binomial Theorem
- Chapter 9 Sequence and Series
- Chapter 10 Straight Lines
- Chapter 11 Conic Sections
- Chapter 12 Introduction to Three-Dimensional Geometry
- Chapter 13 Limits and Derivatives
- Chapter 14 Mathematical Reasoning
- Chapter 15 Statistics
- Chapter 16 Probability