NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations are part of NCERT Exemplar Class 11 Maths . Here we have given NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations.
NCERT Exemplar Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations
Short Answer Type Questions

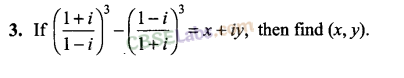
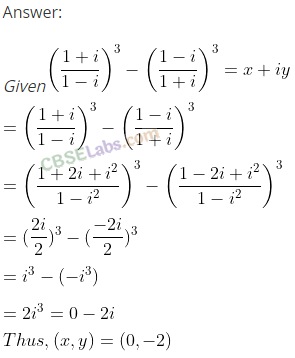
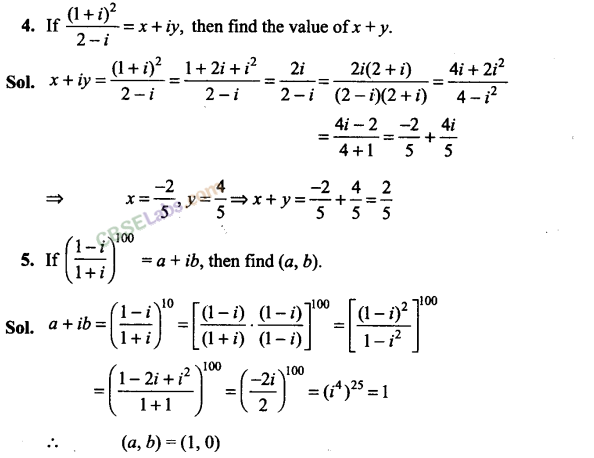
Q6. If a = cos θ + i sin θ, then find the value of (1+a/1-a)
Sol:
a = cos θ + i sin θ
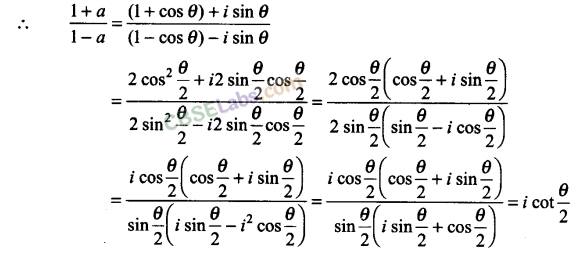

Q10. Show that the complex number z, satisfying the condition arg lies on arg (z-1/z+1) = π/4 lies on a circle.
Sol:
Let z = x +
iy
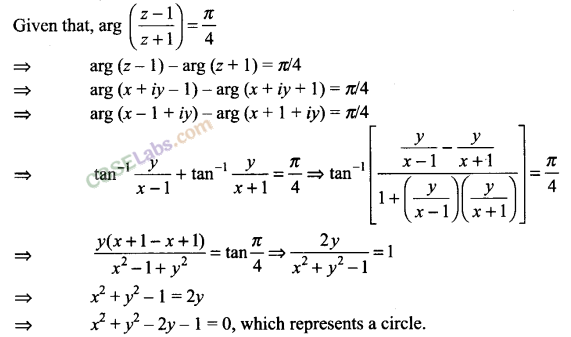
Q11. Solve the equation |z| = z + 1 + 2i.
Sol:
We have |z| = z + 1 + 2i
Putting z = x + iy, we get
|x + iy| = x + iy + 1+2i
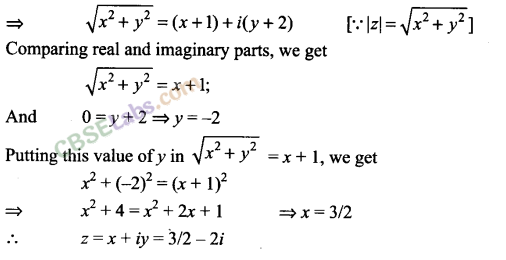
Long Answer Type Questions
Q12. If |z + 1|
= z + 2( 1 + i), then find the value of z.
Sol:
We have |z + 1
1
= z + 2(1+ i)
Putting z = x +
iy,
we get
Then, |x +
iy
+ 1
1
= x +
iy
+ 2(1 + i)
⟹
|x +
iy
+
l|=x
+
iy
+ 2(1
+i)
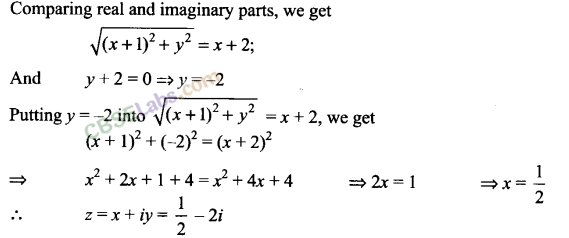
Q13. If arg (z – 1) = arg (z + 3i), then find (x – 1) : y, where z = x + iy.
Sol:
We have arg (z – 1) = arg (z + 3i), where z = x + iy
=> arg (x + iy – 1) = arg (x + iy + 3i)
=> arg (x – 1 + iy) = arg [x + i(y + 3)]
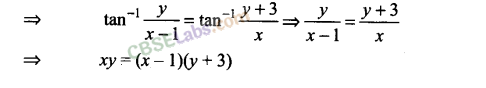
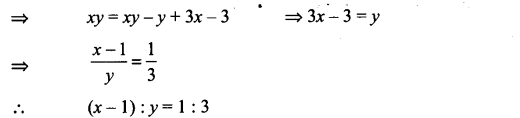
Q14. Show that | z-2/z-3| = 2 represents a circle . Find its center and radius .
Sol:
We have | z-2/z-3| = 2
Puttingz=x + iy, we get
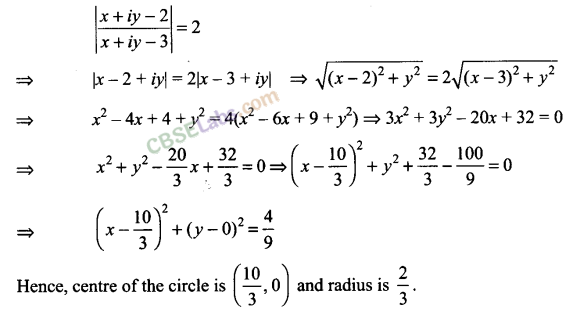
Q15. If z-1/z+1 is a purely imaginary number (z ≠1), then find the value of |z|.
Sol:
Let z = x + iy
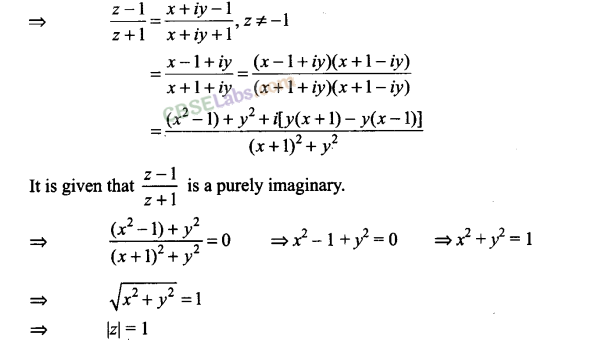
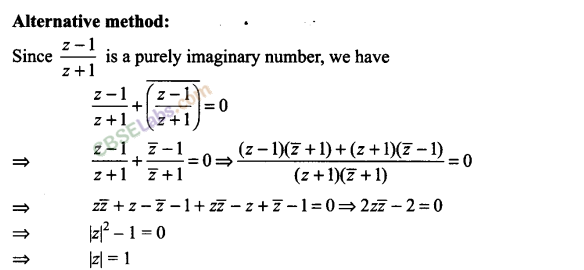

Q17. If |z
1
| = 1 (z
1
≠ -1) and z
2
= z
1
– 1/ z
1
+ 1 , then show that real part of z
2
is zero
.

Q18. If Z
1
, Z
2
and Z
3
, Z
4
are two pairs of conjugate complex numbers, then find arg (Z
1/
Z
4
) + arg (Z
2/
Z
3
)
Sol. It is given that z
1
and z
2
are conjugate complex numbers.

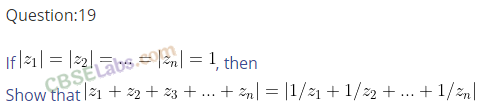
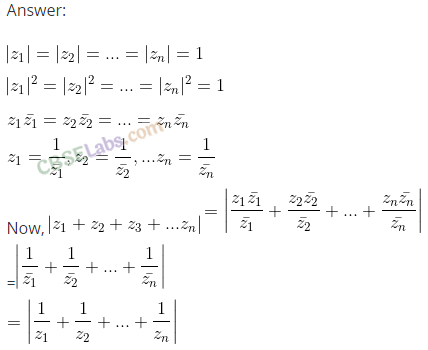
Q20. If for complex number z 1 and z 2 , arg (z 1 ) – arg (z 2 ) = 0, then show that |z 1 – z 2 | = | z 1 |- |z 2 |
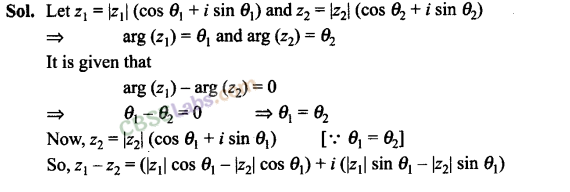

Q21. Solve the system of equations Re (z 2 ) = 0, |z| = 2.
Sol:
Given that, Re(z
2
) = 0, |z| = 2
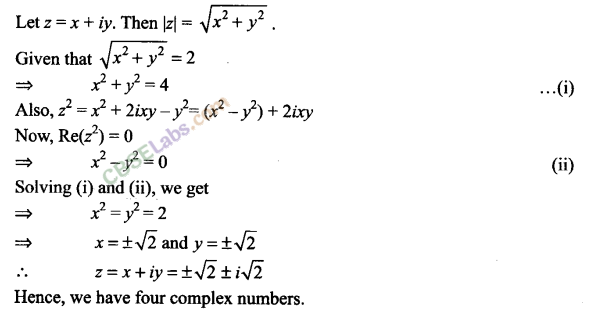
Q22. Find the complex number satisfying the equation z + √2 |(z + 1)| + i = 0.
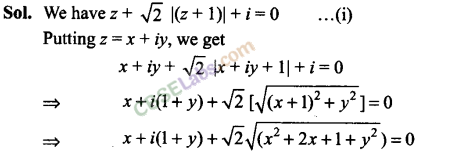
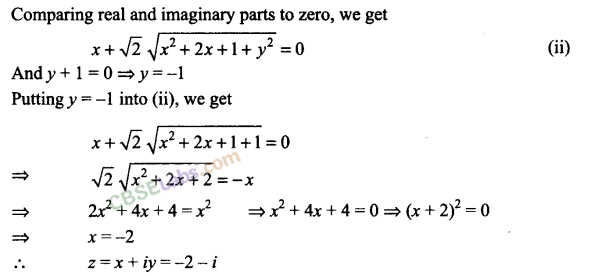

Fill in the blanks



True/False Type Questions
Q26. State true or false for the following.
(i) The order relation is defined on the set of complex numbers.
(ii) Multiplication of a non-zero complex number by -i rotates the point about origin through a right angle in the anti-clockwise direction.
(iii) For any complex number z, the minimum value of |z| + |z – 11 is 1.
(iv) The locus represented by |z — 11= |z — i| is a line perpendicular to the join of the points (1,0) and (0, 1).
(v) If z is a complex number such that z ≠ 0 and Re(z) = 0, then Im (z
2
) = 0.
(vi) The inequality |z – 4| < |z – 2| represents the region given by x > 3.
(vii) Let Z
1
and Z
2
be two complex numbers such that |z, + z
2
| = |z
1
j + |z
2
|, then arg (z
1
– z
2
) = 0.
(viii) 2 is not a complex number.
Sol:
(i) False
We can compare two complex numbers when they are purely real. Otherwise comparison of complex numbers is not possible or has no meaning.
(ii) False


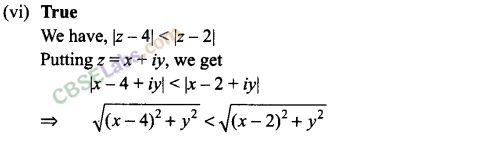

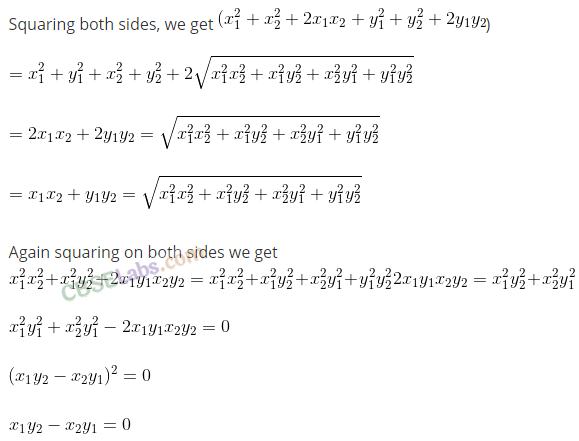

Matching Column Type Questions
Q24. Match the statements of Column A and Column B.
| Column A | Column B | ||
| (a) | The polar form of i + √3 is | (i) | Perpendicular bisector of segment joining (-2, 0) and (2,0) |
| (b) | The amplitude of- 1 + √-3 is | (ii) | On or outside the circle having centre at (0, -4) and radius 3. |
| (c) | It |z + 2| = |z – 2|, then locus of z is | (iii) | 2/3 |
| (d) | It |z + 2i| = |z – 2i|, then locus of z is | (iv) | Perpendicular bisector of segment joining (0, -2) and (0,2) |
| (e) | Region represented by |z + 4i| ≥ 3 is | (v) | 2(cos /6 +I sin /6) |
| (0 | Region represented by |z + 4| ≤ 3 is | (Vi) | On or inside the circle having centre (-4,0) and radius 3 units. |
| (g) | Conjugate of 1+2i/1-I lies in | (vii) | First quadrant |
| (h) | Reciprocal of 1 – i lies in | (viii) | Third quadrant |



Q28. What is the conjugate of 2-i / (1 – 2i)
2
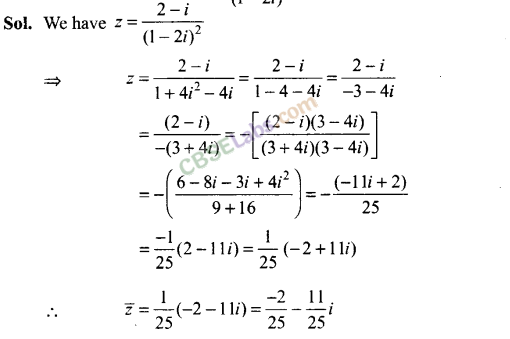
Q29. If |Z
1
| = |Z
2
|, is it necessary that Z
1
= Z
2
?
Sol:
If |Z
1
| = |Z
2
| then z
1
and z
2
are at the same distance from origin.
But if arg(Z
1
) ≠arg(z
2
), then z
1
and z
2
are different.
So, if (z
1
| = |z
2
|, then it is not necessary that z
1
= z
2
.
Consider Z
1
= 3 + 4i and Z
2
= 4 + 3i
Q30.If (a
2
+1)
2
/ 2a –i = x + iy, then what is the value of x
2
+ y
2
?
Sol:
(a
2
+1)
2
/ 2a –i = x + iy

Q31. Find the value of z, if |z| = 4 and arg (z) = 5π/6
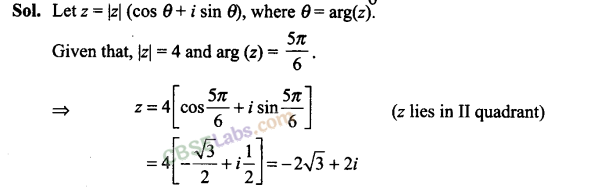




Q34. Where does z lies, if | z – 5i / z + 5i | = 1?
Sol:
We have | z – 5i / z + 5i |

Instruction for Exercises 35-40: Choose the correct answer from the given four options indicated against each of the Exercises.
Q35. sin x + i cos 2x and cos x – i sin 2x are conjugate to each other for
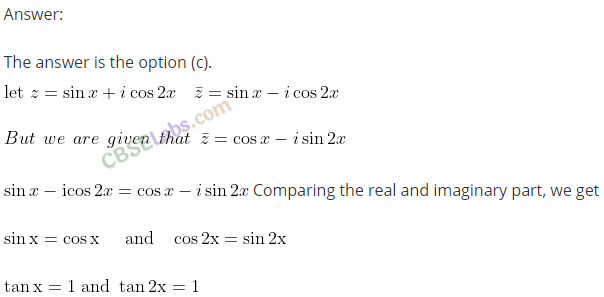

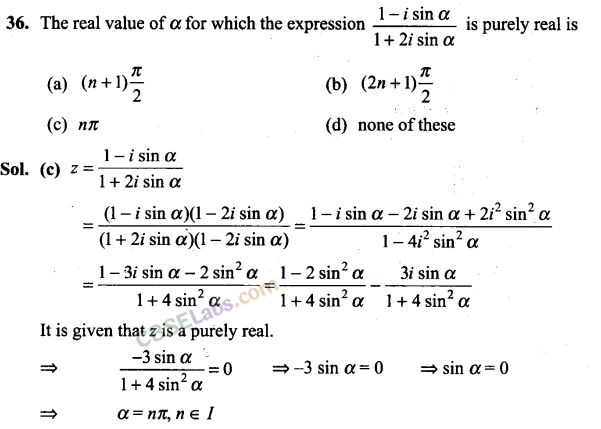

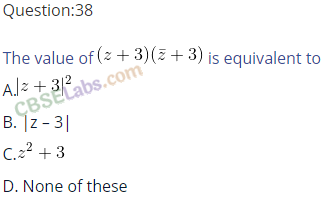
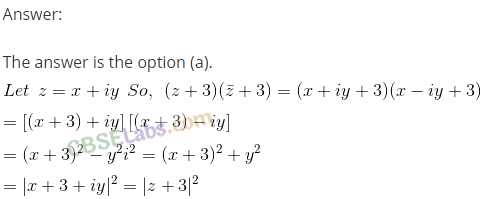
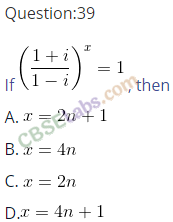

Question 40.
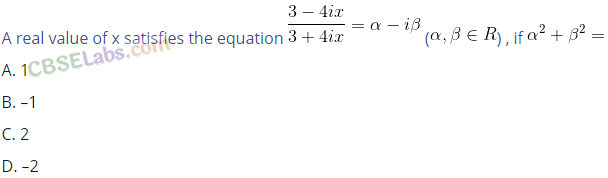
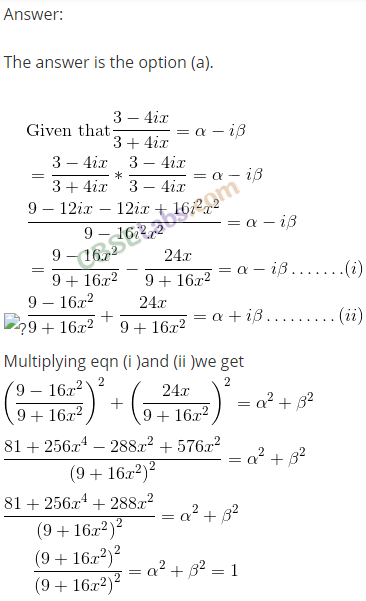
Q41. Which of the following is correct for any two complex numbers z
1
and z
2
?
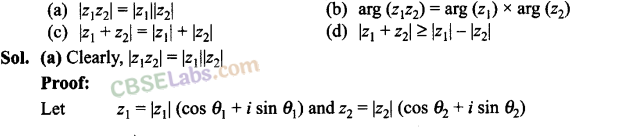
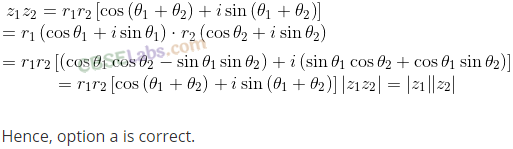
NCERT Exemplar Class 11 Maths Solutions
- Chapter 1 Sets
- Chapter 2 Relations and Functions
- Chapter 3 Trigonometric Functions
- Chapter 4 Principle of Mathematical Induction
- Chapter 5 Complex Numbers and Quadratic Equations
- Chapter 6 Linear Inequalities
- Chapter 7 Permutations and Combinations
- Chapter 8 Binomial Theorem
- Chapter 9 Sequence and Series
- Chapter 10 Straight Lines
- Chapter 11 Conic Sections
- Chapter 12 Introduction to Three-Dimensional Geometry
- Chapter 13 Limits and Derivatives
- Chapter 14 Mathematical Reasoning
- Chapter 15 Statistics
- Chapter 16 Probability