NCERT Exemplar Class 11 Maths Chapter 3 Trigonometric Functions

NCERT Exemplar Class 11 Maths Chapter 3 Trigonometric Functions are part of NCERT Exemplar Class 11 Maths . Here we have given NCERT Exemplar Class 11 Maths Chapter 3 Trigonometric Functions.

NCERT Exemplar Class 11 Maths Chapter 3  Trigonometric Functions

Q4. If cos (α + ) =4/5 and sin (α- )=5/13 , where α lie between 0 and π/4, then find the value of tan 2α.

Sol:

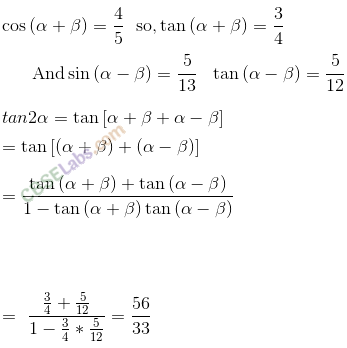
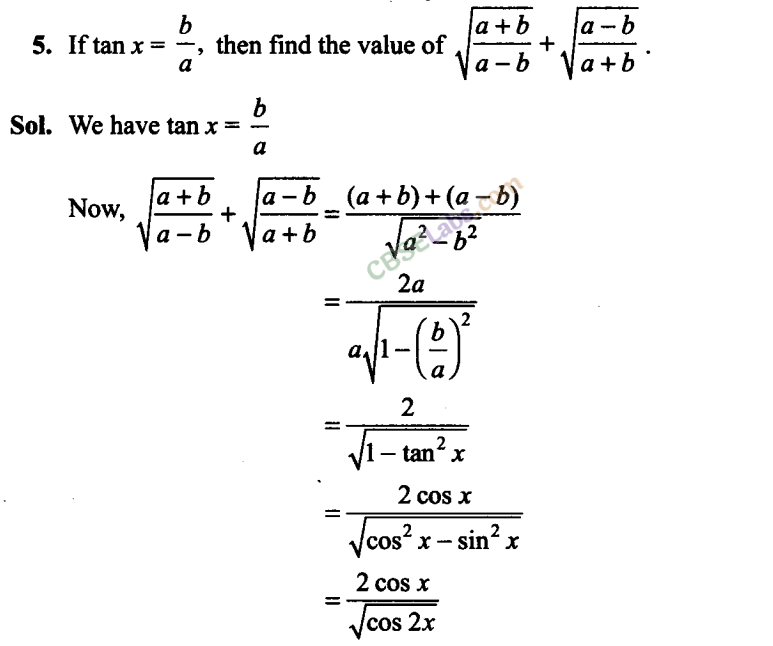
Q6. Prove that cos cos /2- cos 3 cos 9/2 = sin 7/2 sin 4 .

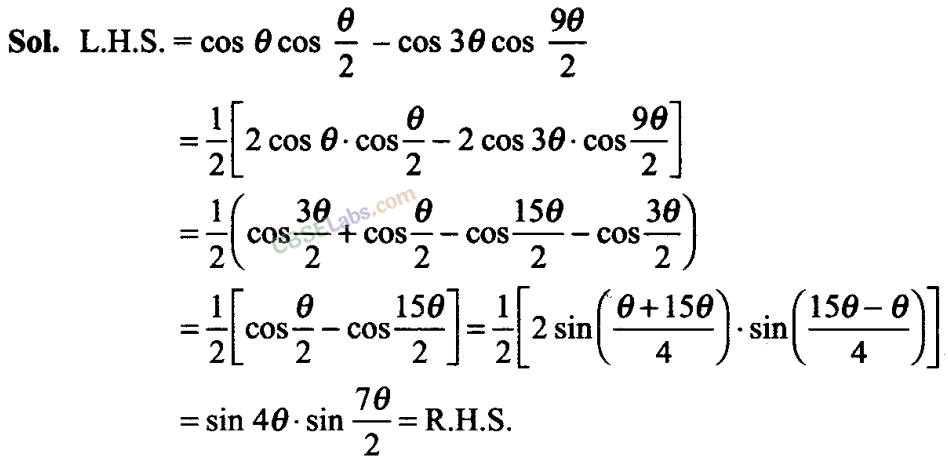
Q7. If a cos θ + b sin θ =m and a sin θ -b cosθ = n, then show that a ² + b ² -m ² + n ²

Sol: We have, a cos θ + b sin θ = m (i)
and a sin θ -bcos θ = n (ii)

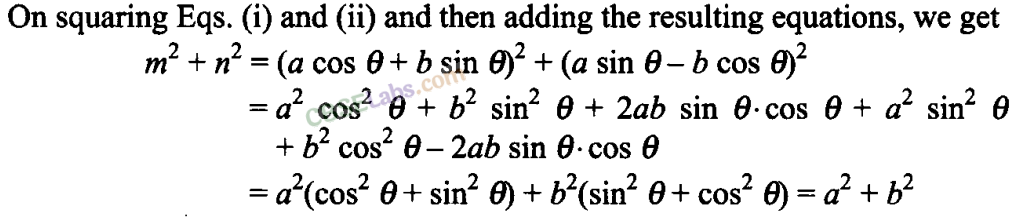
Q8. Find the value of tan 22°30′

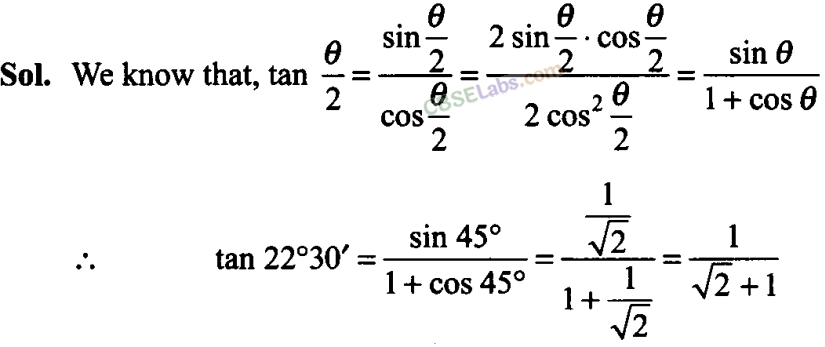
Q9. Prove that sin 4A = 4 sin A cos ³ A – 4 cos A sin ³ A.

Sol: L.H.S. = sin 4A
= 2 sin 2A- cos 2A = 2(2 sin A cosA)(cos ² A – sin ² A)
= 4 sin A • cos ³ A – 4 cos A sin ³ A = R.H.S.

Q10. If tan + sin = m and tan – sin = n, then prove that m ² -n ² = 4 sin tan

Sol: We have, tan + sin = m   (i)
And tan -sin =n  (ii)
Now,         m + n = 2 tan
And          m – n = 2 sin.
(m + n)(m -n) = 4 sin 6
tan m ² -n ² = 4 sin -tan

Q11. If tan (A + B) =p and tan (A – B) = q, then show that tan 2A = p+q / 1 – pq

Sol: We have tan (A + B) =p and tan (A – B) = q
tan2A = tan [(A + B) + (A-B)]

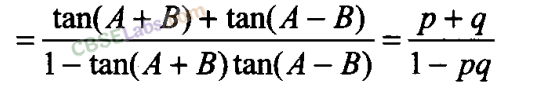
Q12. If cos + cos = 0 = sin + sin β, then prove that cos 2 + cos 2β = -2 cos (α + ).

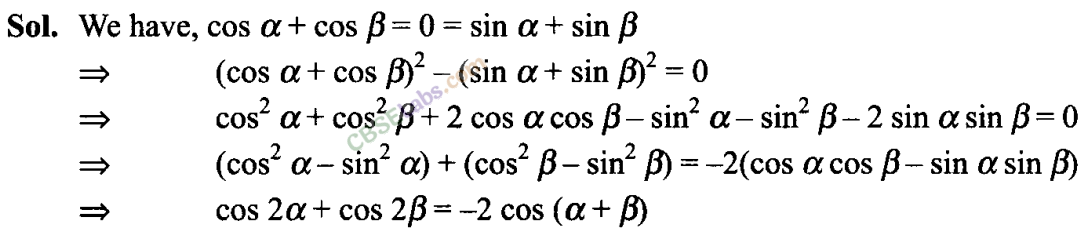
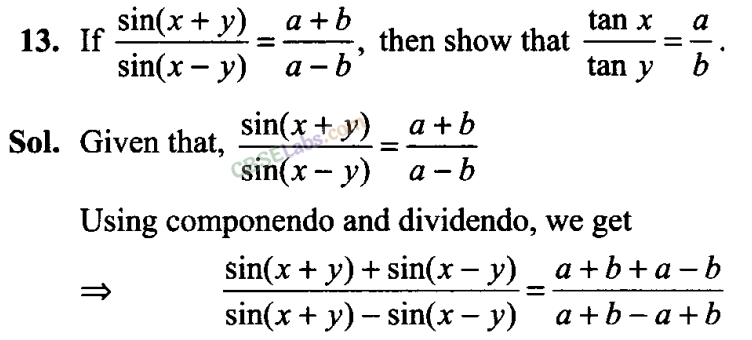
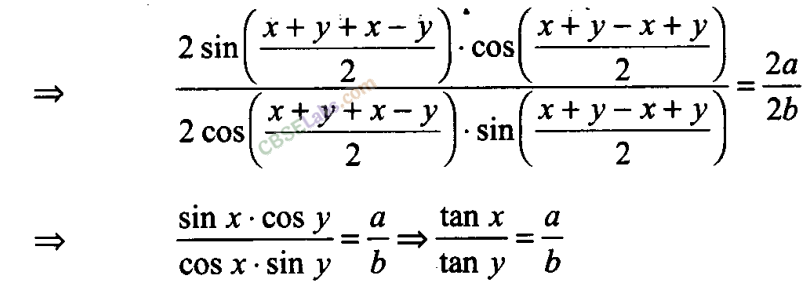
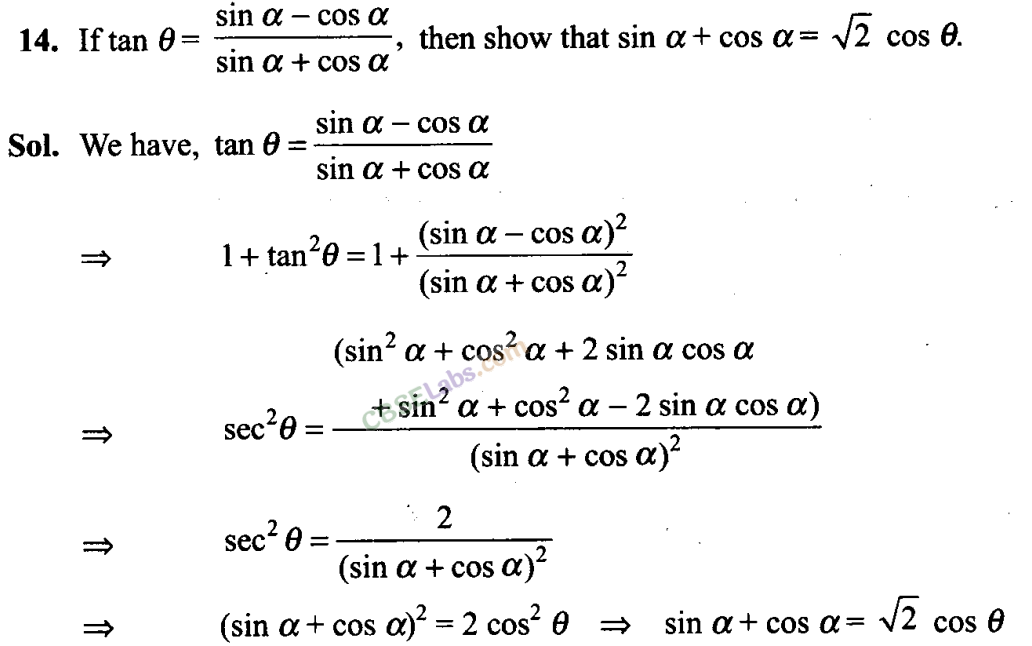
Q15.  If sin θ+ cos θ =1, then find the general value of θ

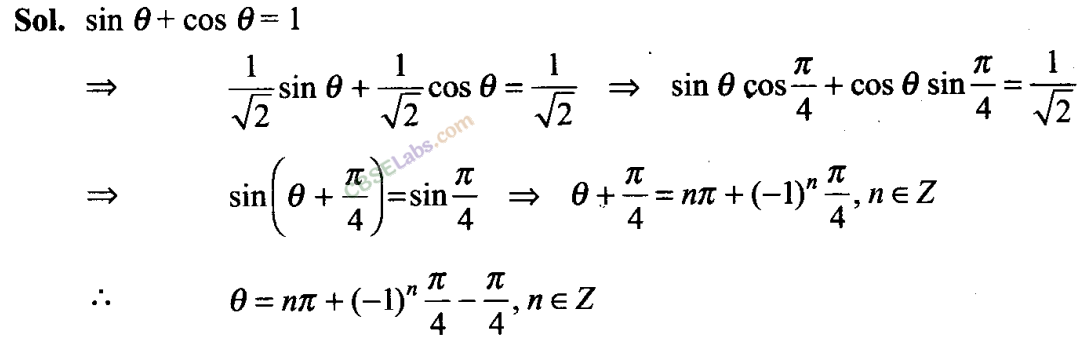
Q16. Find the most general value of θ satisfying the equation tan θ = -1 and cos θ = 1/√2 .
Sol: We have tan θ = -1 and cos θ =1/√2 .
So, θ lies in IV quadrant.
θ = 7/4
So, general solution is θ = 7π/4 + 2 n π, n∈ Z

Q17. If cot θ + tan θ = 2 cosec θ, then find the general value of θ
Sol: Given that, cot θ + tan θ = 2 cosec θ

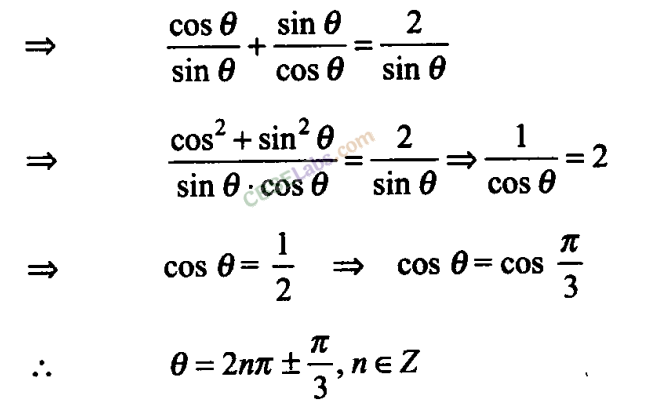
Q18. If 2 sin ² θ =3 cos θ, where O≤θ≤2, then find the value of θ

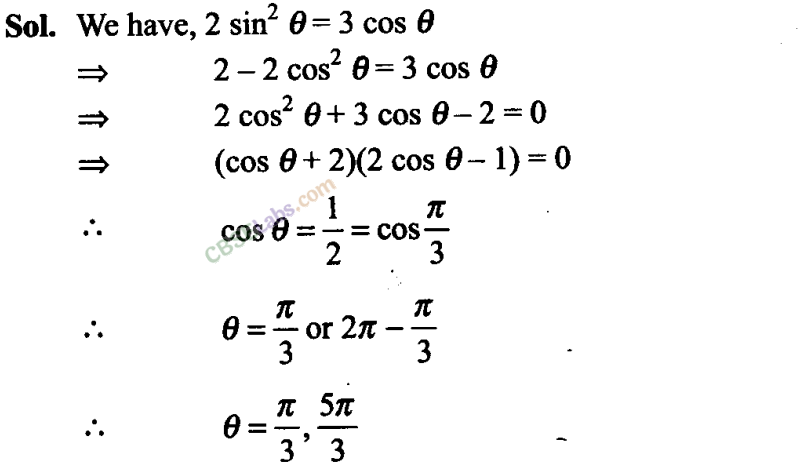
Q19. If sec x cos 5x + 1 = 0, where 0 < x <π/2 , then find the value of x.

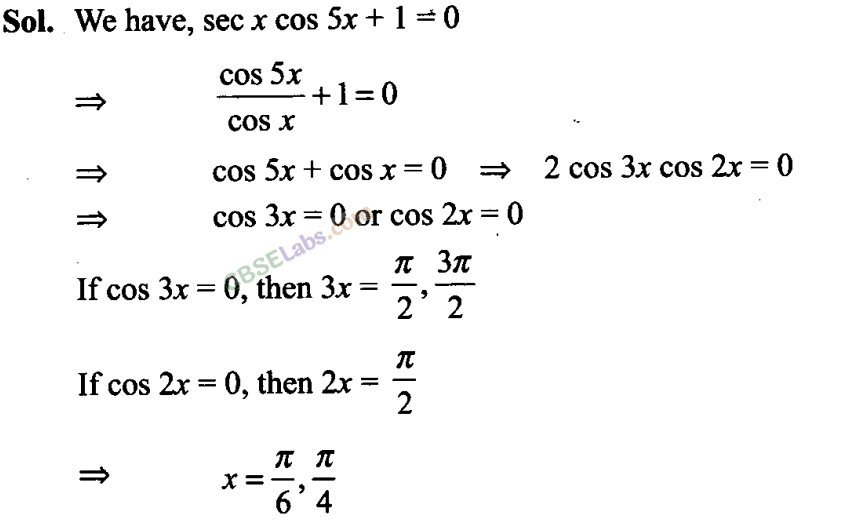
Long Answer Type Questions

Q20. If sin(θ + α) = a and sin(θ + β) = b , then prove that cos2(α – β) – 4abcos(α – β) = 1-2a ² -2b ²

Sol: We have sin(θ + α) = a —(i)
sin(θ + β) = b ——-(ii)

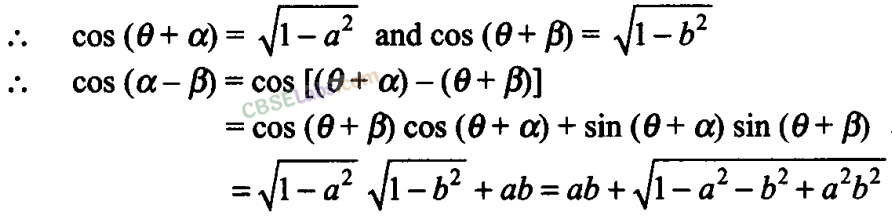
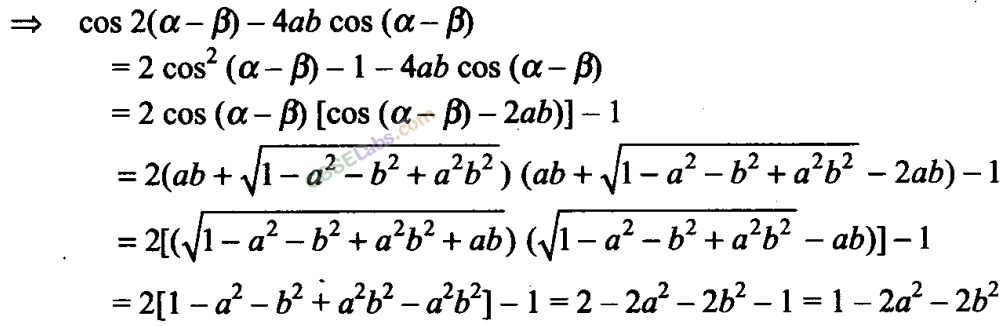
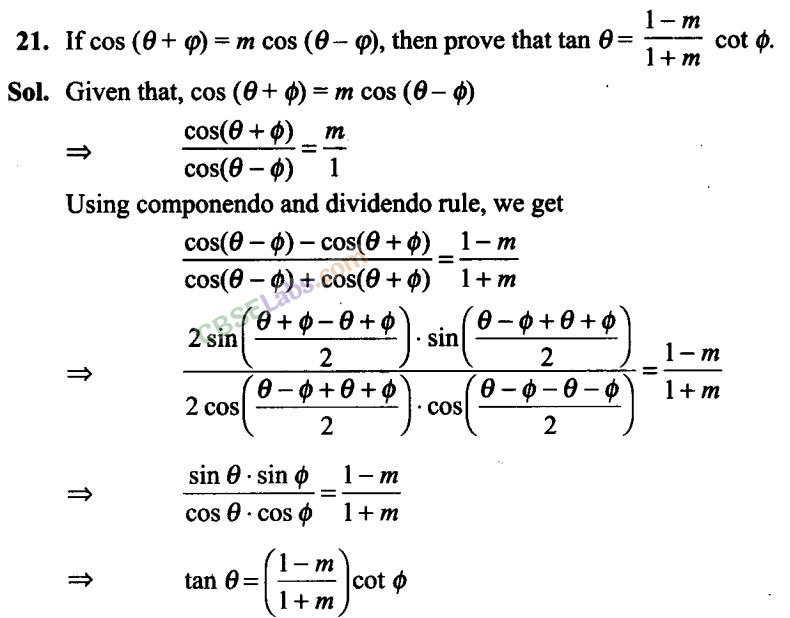
Q22. Find the value of the expression

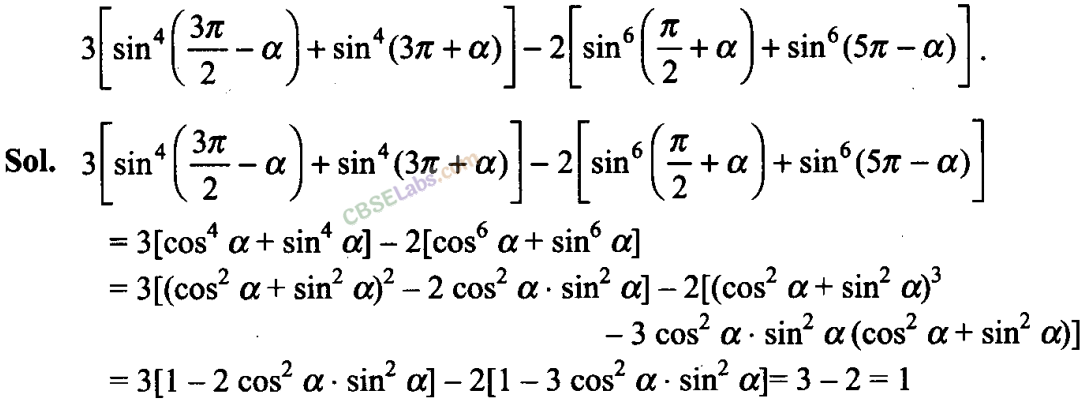
Q23. If a cos 2+b sin 2 = c has α and β as its roots, then prove that tan α +tan β = 2b/a+c

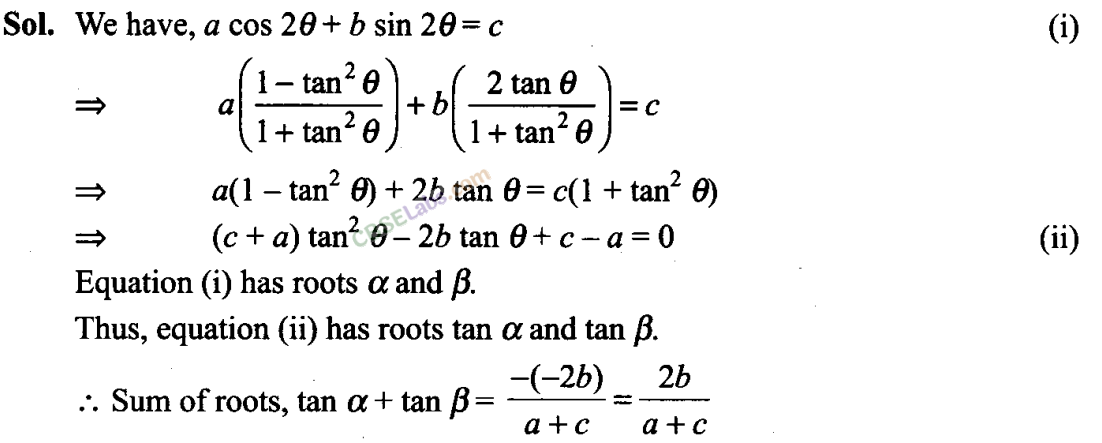
Q24. If x = sec ϕ-tanϕandy = cosec ϕ + cot ϕ then show that xy + x -y +1=0.

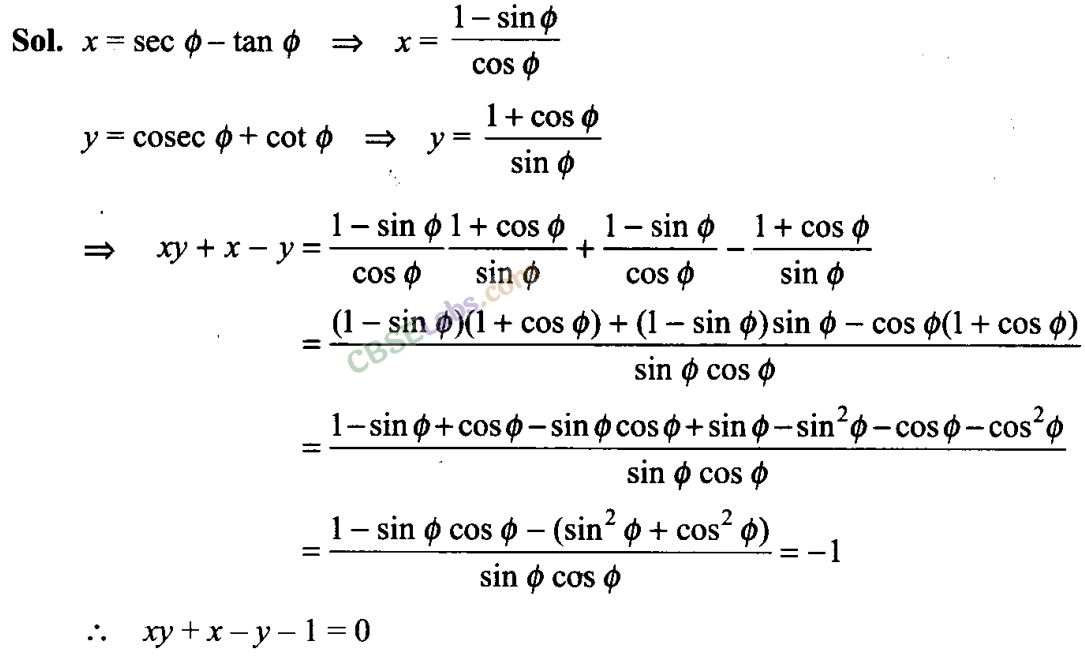
Q25. If lies in the first quadrant and cos =8/17 , then find the value of cos (30° + ) + cos (45° – ) + cos (120° – ).

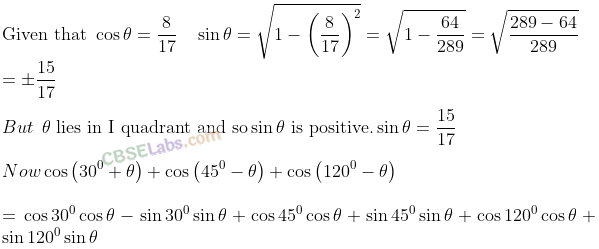
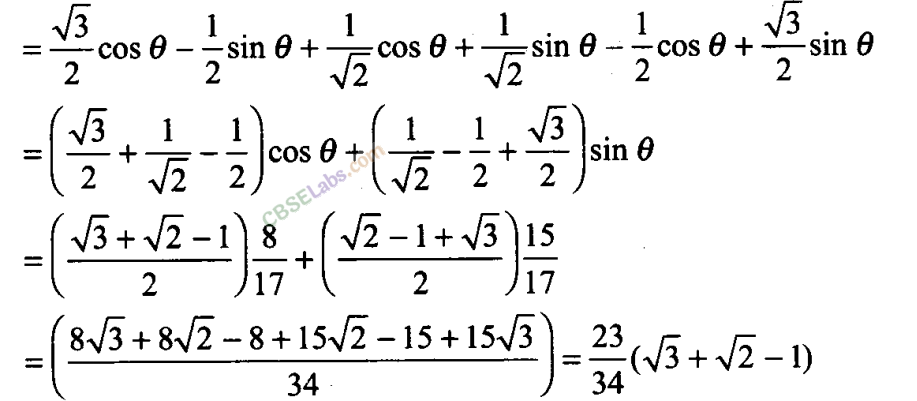
Q26. Find the value of the expression cos ⁴ π/8 + cos ⁴ 3π/8  + cos ⁴ 5π/8  + cos ⁴ 7π/8

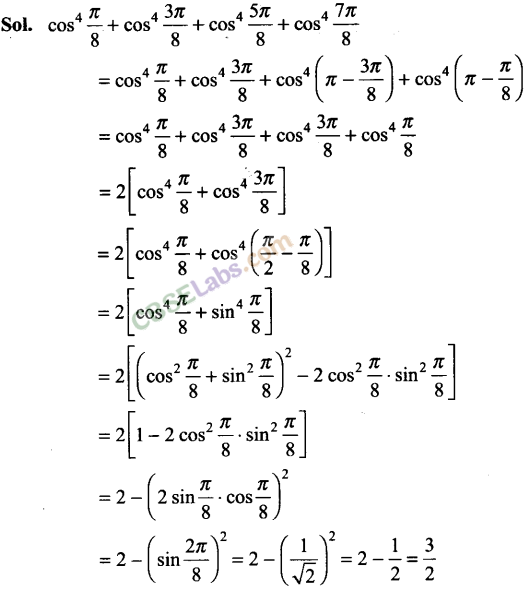
Q27. Find the general solution of the equation 5 cos ² +7 sin ² -6 = 0.

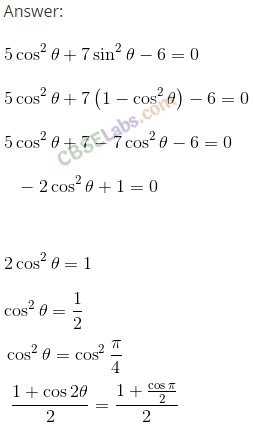
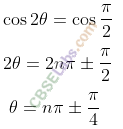
Q28. Find the general solution of‘the equation sin x – 3 sin 2x + sin 3x = cos x – 3 cos 2x + cos 3x.
Sol: We have, (sin x + sin 3x) – 3 sin 2x = (cos x + cos 3x) – 3 cos 2x
=> 2 sin 2x cos x – 3 sin 2x = 2 cos 2x.cos x – 3 cos 2x
=> sin 2x(2 cos x – 3) = cos 2x(2 cos x – 3)
=> sin 2x = cos 2x (As cos x ≠ 3/2)
=>              tan 2x = 1    => tan 2x = tan π/4
=>              2x = nπ + π/4 , n∈Z
x = nπ/2 +π/8 , n∈Z

Q29. Find the general solution of the equation (√3- l)cos + (√3+ 1)sin = 2.

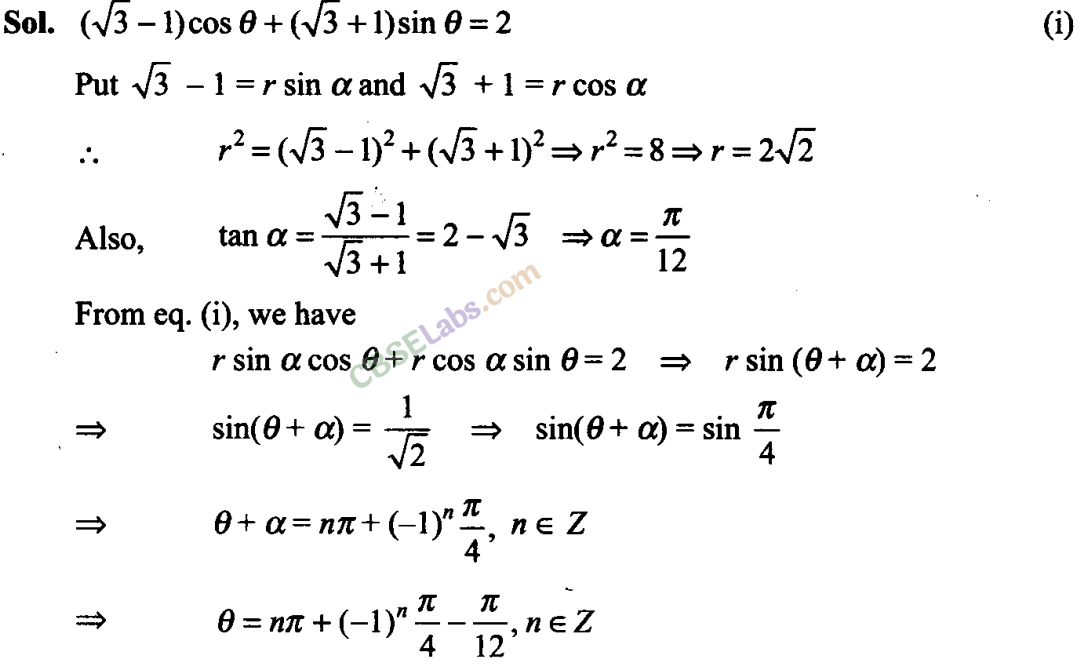
Objective Type Questions

Q30. If sin + cosec =2, then sin ² + cosec ² is equal to
(a) 1
(b) 4
(c) 2
(d) None of these

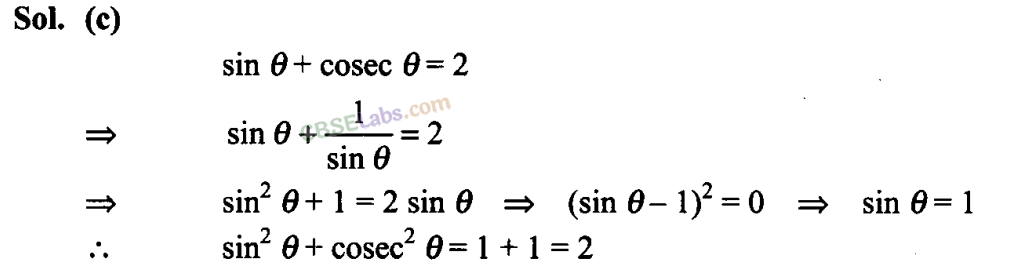
Q31. If f(x) = cos ² x + sec ² x, then ‘
(a) f(x) <1
(b) f(x) = 1
(c) 2 <f(x) < 1
(d) fx) ≥ 2

Q32. If tan θ = 1/2 and tan ϕ = 1/3, then the value of θ + ϕ is

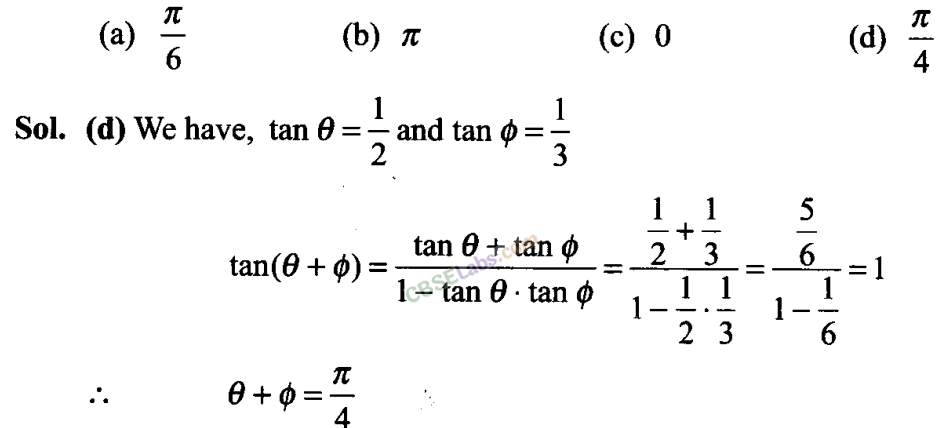
Q33. Which of the following is not correct?

(a) sin θ = – 1/5 (b) cos θ = 1                 (c) sec θ = -1/2         (d) tan θ = 20
Sol: (c)
We know that, the range of sec θ is R – (-1, 1).
Hence, sec θ cannot be equal to -1/2

Q34. The value of tan 1° tan 2° tan 3° … tan 89° is
(a) 0
(b) 1
(c) 1/2
(d) Not defined

Sol: (b)
tan 1° tan 2° tan 3° … tan 89°
= [tan 1° tan 2° … tan 44°] tan 45°[tan (90° – 44°) tan (90° – 43°)… tan (90° – 1°)]
= [tan 1° tan 2° … tan 44°] [cot 44° cot 43°……. cot 1°]
= 1-1… 1-1 = 1

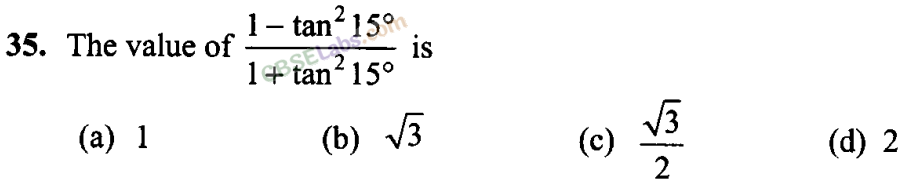
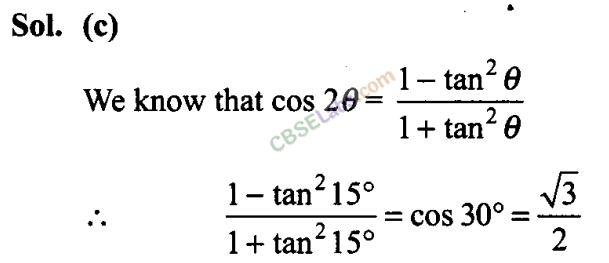
Q36. The value of cos 1° cos 2° cos 3° … cos 179° is
(a) 1/ √ 2
(b) 0
(c) 1
(d) -1

Sol: (b)
Since cos 90° = 0, we have
cos 1° cos 2° cos 3° …cos 90°… cos 179° = 0

Q37. If tan θ = 3 and θ lies in the third quadrant, then the value of sin θ is

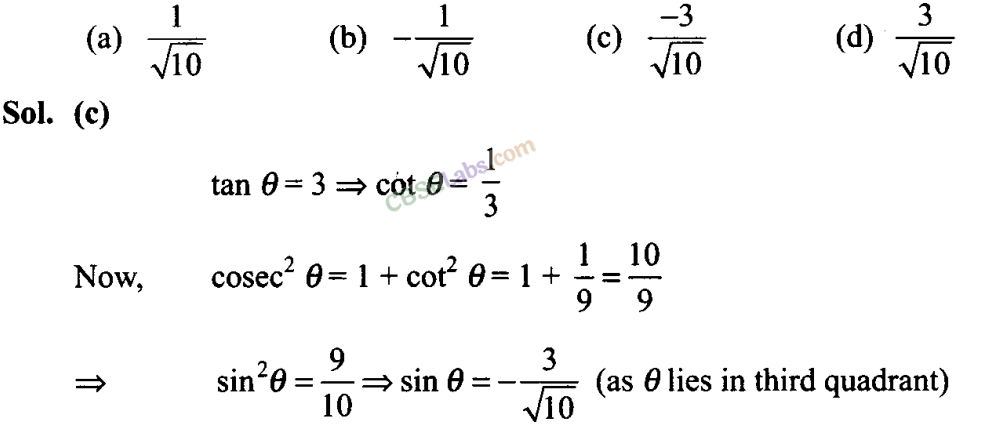
Q38. The value of tan 75° – cot 75° is equal to

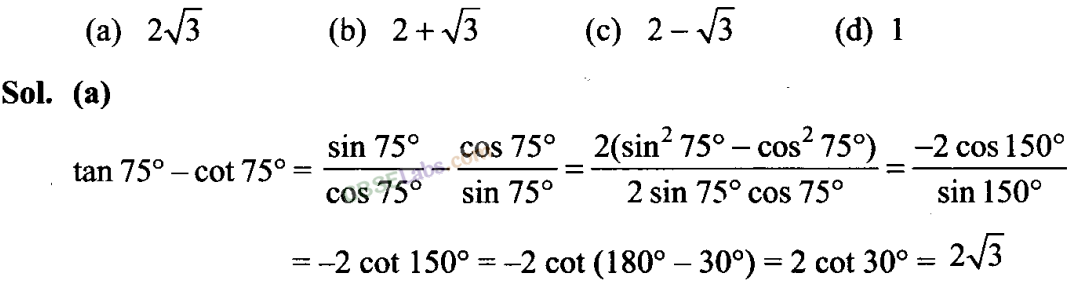
Q39. Which of the following is correct?
(a) sin 1° > sin 1
(b) sin 1° < sin 1
(c) sin l° = sin l
(d) sin l° = π/18° sin 1

Sol: We know that, in first quadrant if θ is increasing, then sin θ is also increasing.
∴sin 1° < sin 1 [∵ 1 radian = 57◦30′]

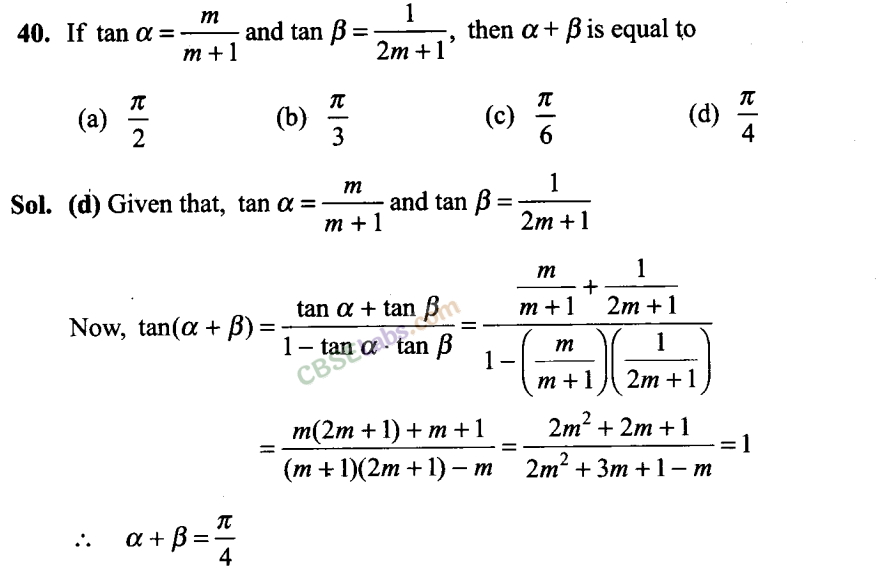
Q41. The minimum value of 3 cos x + 4 sin x + 8 is
(a) 5
(b) 9
(c) 7
(d) 3
Sol: (d)
3 cos x + 4sin x + 8 = 5 (3/5 cos x + 4/5sin x) + 8
= 5(sin α cos x + cos α sin x) + 8
= 5 sin(α + x) + 8, where tan α = 3/4

Q42. The value of tan 3A – tan 2A – tan A is
(a) tan 3A . tan 2A . tan A
(b) -tan 3A .tan 2A . tan A
(c) tan A . tan 2A – tan 2A . tan 3A – tan 3A . tan A
(d) None of these
Sol: (a)
3A= A+ 2A
=> tan 3A = tan (A + 2A)
=> tan 3 A = tanA + tan2A/ 1 – tan A . tan 2A
=> tan A + tan 2A = tan 3A – tan 3A• tan 2A . tan A
=> tan 3 A – tan 2A – tan A = tan 3A . tan 2A . tan A

Q43. The value of sin (45° + )- cos (45° – ) is
(a) 2 cos
(b) 2 sin
(c) 1
(d) 0
Sol: (d)
sin (45° + ) – cos (45° – ) = sin (45° + ) – sin (90° – (45° – ))
= sin (45° + ) – sin (45°+ ) = 0

Q44. The value of (π/4+ ) cot (π/4- ) is
(a) -1
(b)  0
(c)  1
(d)   Not defined

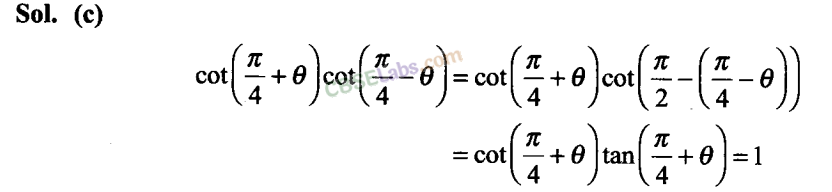
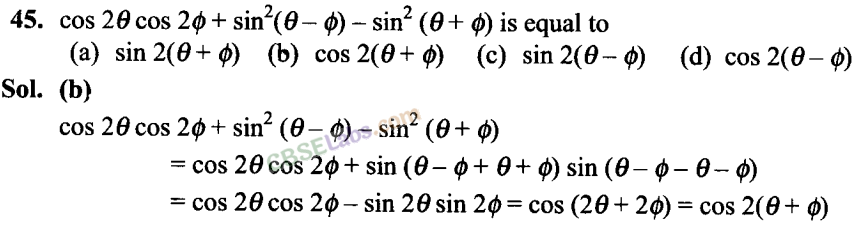
Q46. The value of cos 12° + cos 84° + cos 156° + cos 132° is
(a) 1/2
(b) 1
(c) -1/2
(d) 1/8

Q47. If tan A = 1/2 and tan B = 1/3 then tan (2A + B) is equal to
(a) 1
(b) 2
(c) 3
(d) 4

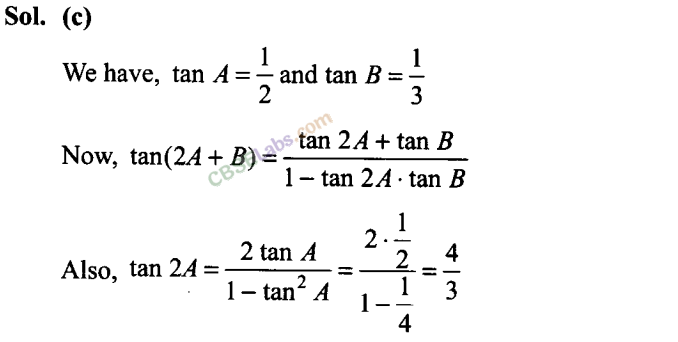
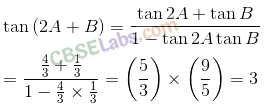
Q49. The value of sin 50° – sin 70° + sin 10° is equal to
(a) 1
(b) 0
(c) 1
(d) 2

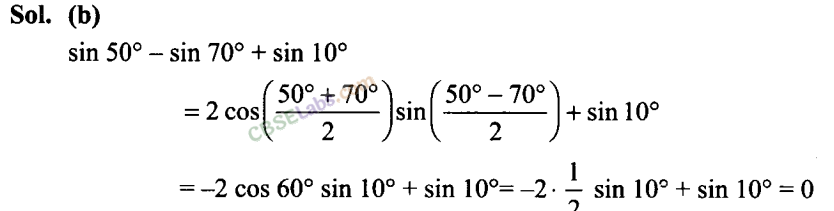
Q50. If sin + cos =1, then the value of sin 2 is
(a) 1
(b) 1
(c) 0
(d) -1

LearnCBSE Online