NCERT Exemplar Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry

NCERT Exemplar Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry are part of NCERT Exemplar Class 11 Maths . Here we have given NCERT Exemplar Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry.

NCERT Exemplar Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry

Short Answer Type Questions

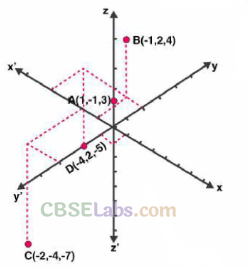
Q1. Locate the following points:

(i) (1,-1, 3),
(ii) (-1,2,4)
(iii) (-2, -4, -7)
(iv) (-4,2, -5)
Sol: Given, coordinates
(i) (1,-1, 3),
(ii) (-1,2,4)
(iii) (-2, -4, -7)
(iv) (-4,2, -5)

Q2. Name the octant in which each of the following points lies.
(i) (1,2,3)
(ii) (4,-2, 3)
(iii) (4,-2,-5)
(iv)(4,2,-5)
(v) (-4,2,5)
(vi) (-3,-1,6)
(vii) (2,-4,-7)
(viii) (-4, 2,-5)

Q3. Let A, B, C be the feet of perpendiculars from a point P on the x, y,z-axes respectively. Find the coordinates of A, B and C in each of the following where the point P is:
(i) (3,4,2)
(ii) (-5,3,7)
(iii) (4,-3,-5)
Sol: We know that, on x-axis, y, z = 0, on y-axis, x, z = 0 and on z-axis, x,y = 0. Thus, the feet of perpendiculars from given point P on the axis are as follows.

(i) A(3,0,0),5(0,4,0),C(0,0,2)
(ii) A(-5, 0, 0), B(0, 3, 0), C(0, 0, 7)
(iii) A(4, 0, 0), 5(0, -3, 0), C(0,0, -5)

Q4. Let A, B, C be the feet of perpendiculars from a point P on the xy, yz and zx- planes respectively. Find the coordinates of A, B, C in each of the following where the point P is
(i) (3,4,5)
(ii) (-5,3,7)
(iii) (4,-3,-5).
Sol: We know that, on xy-plane z = 0, on yz-plane, x = 0 and on zx-plane, y = 0. Thus, the coordinates of feet of perpendicular on the xy, yz and zx-planes from the given point are as follows:
(i) A(3,4,0), 5(0,4, 5), C(3,0,5)
(ii) A(-5, 3,0), 5(0, 3, 7), C(-5, 0, 7)
(iii) A(4, -3, 0), 5(0, -3, -5), C(4,0, -5)

Q5. How far apart are the points (2,0, 0) and (-3, 0, 0)?
Sol: Given points are A (2, 0, 0) and 5(-3,0, 0).
AB = |2 – (-3)| = 5

Q6. Find the distance from the origin to (6, 6, 7).
Sol: Distance form origin to the point (6, 6, 7)

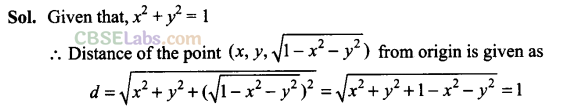
Q8. Show that the point ,4(1, -1, 3), 6(2, -4, 5) and (5, -13, 11) are collinear.
Sol: Given points are ,4(1, -1, 3), 6(2, -4, 5) and C(5, -13, 11).

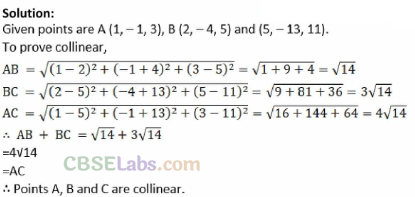
Q9. Three consecutive vertices of a parallelogram ABCD are .4(6, -2,4), 6(2,4, -8), C(-2, 2, 4). Find the coordinates of the fourth vertex.
Sol: Let the coordinates of the fourth vertex D be (x, y, z).

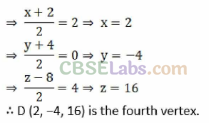
Q10 .Show that the triangle ABC with vertices .4(0,4,1), 6(2,3, -1) and C(4, 5,0) is right angled.
Sol: The vertices of ∆ABC are A(0,4, 1), 5(2, 3, -1) and C(4, 5, 0).

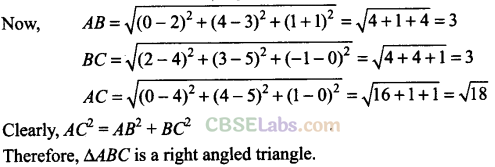
Q11. Find the third vertex of triangle whose centroid is origin and two vertices are (2,4,6) and (0, -2, -5).
Sol: Let the third or unknown vertex of ∆ABC be A(x, y, z).
Other vertices of triangle are 5(2,4, 6) and C(0, -2, -5).
The centroid is G(0, 0, 0).

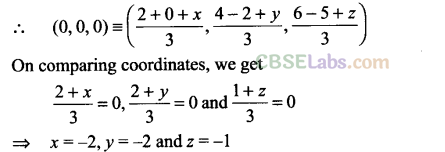
Q12. Find the centroid of a triangle, the mid-point of whose sides are D (1,2, – 3), E(3,0, l)and F(-l, 1,-4).
Sol: Given that, mid-points of sides of AABC are D(l, 2, -3), E(3, 0, 1) and F(-l, 1,-4).

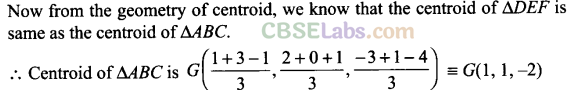
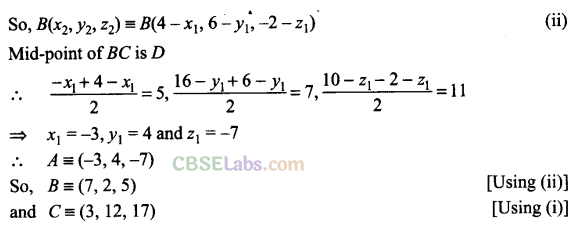
Q14. Three vertices of a Parallelogram ABCD are A(\, 2, 3), B(-A, -2, -1) and C(2, 3, 2). Find the fourth vertex
Sol: Let the fourth vertex of the parallelogram D(x, y, z).
Mid-point of BD

Q15. Find the coordinate of the points which trisect the line segment joining the points .A(2, 1, -3) and B(5, -8, 3).

Q16. If the origin is the centroid of a triangle ABC having vertices A(a, 1, 3), B(-2, b, -5) and C(4, 7, c), find the values of a, b, c.
Sol: Vertices of AABC are A(a, 1, 3), B(-2, b, -5) and C(4, 7, c).
Also, the centroid is G(0, 0, 0).

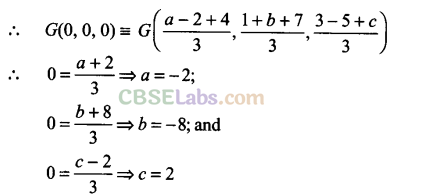
Q17. Let A(2, 2, -3), 5(5, 6, 9) and C(2, 7, 9) be the vertices of a triangle. The internal bisector of the angle A meets BC at the point Find the coordinates of D.

Long Answer Type Questions

Q18. Show that the three points A(2, 3, 4), 5(-l, 2, -3) and C(-4, 1, -10) are collinear and find the ratio in which Cdivides
Sol: Given points are A(2, 3, 4), B(-1, 2, -3) and C(-4,1,-10)

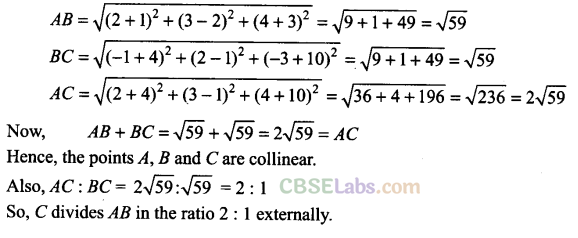
Q19. The mid-point of the sides of a triangle are (1, 5, -1), (0,4, -2) and (2, 3,4). Find its vertices. Also, find the centroid of the triangle.
Sol: Given that mid-points of the sides of AABC are D( 1, 5, -1), E(0, 4, -2) and F(2, 3,4).

Q20. Prove that the points (0, -1, -7), (2, 1, -9) and (6, 5, -13) are collinear. Find the ratio in which the first point divides the join of the other two.
Sol: Given points are 4(0, -1, -7), 8(2, 1, -9) and C(6, 5, -13).

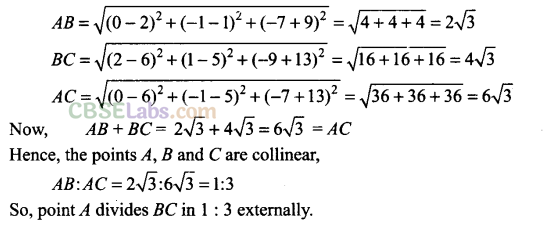
Q21. What are the coordinates of the vertices of a cube whose edge is 2 units, one of whose vertices coincides with the origin and the three edges passing through the origin, coincides with the positive direction of the axes through the origin?
Sol: The coordinate of the cube whose edge is 2 units, are:
(2, 0, 0), (2,2, 0), (0, 2, 0), (0, 2,2), (0, 0,2), (2,0, 2), (0, 0, 0) and (2,2, 2)

Objective Type Questions

Q22. The distance of point P(3,4, 5) from the yz-plane is
(a) 3 units
(b) 4 units
(c) 5 units
(d) 550
Sol: (a) Given point is P{3,4, 5).
Distance of P from yz-plane = |x coordinate of P| = 3

Q23. What is the length of foot of perpendicular drawn from the point P(3,4, 5) on y-axis?

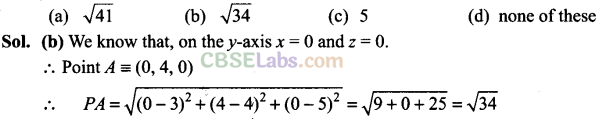
Q24. Distance of the point (3,4, 5) from the origin (0, 0, 0) is

Q25. If the distance between the points (a,0,1) and (0,1,2) is √27, then the value of a is
(a)     5
(b)     ± 5
(c)     -5
(d)   none of these

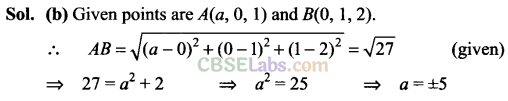
Q26. x-axis is the intersection of two planes
(a) xy and xz
(b) yz and zx
(c) xy and yz
(d) none of these
Sol: (a) We know that, on the xy and xz-planes, the line of intersection is x-axis.

Q27. Equation of Y-axis is considered as
(a) x = 0, y = 0
(b) y = 0, z = 0
(c) z = 0, x = 0
(d) none of these
Sol: (c) On the j-axis, x = 0 and z = 0.

Q28. The point (-2, -3, -4) lies in the
(a) First octant
(b) Seventh octant
(c) Second octant
(d) Eighth octant
Sol: (b) The point (-2, -3, -4) lies in seventh octant.

Q29. A plane is parallel to yz-plane so it is perpendicular to
(a) x-axis
(b) y-axis
(c) z-axis
(d) none of these
Sol: (a) A plane parallel to yz-plane is perpendicular to x-axis.

Q30. The locus of a point for which y = 0, z = 0 is
(a)    equation of x-axis
(b)    equation of y-axis
(c)     equation at z-axis
(d)    none of these
Sol: (a) We know that, equation of the x-axis is: y = 0, z = 0 So, the locus of the point is equation of x-axis.

Q31. The locus of a point for which x = 0 is
(a)    xy-plane
(b)    yz-plane
(c)     zx-plane
(d)    none of these
Sol: (b) On the yz-plane, x = 0, hence the locus of the point is yz-plane.

Q32. If a parallelepiped is formed by planes drawn through the points (5,8,10) and (3, 6, 8) parallel to the coordinate planes, then the length of diagonal of the parallelepiped is

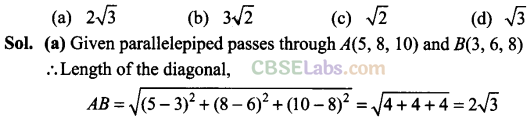
Q33. L is the foot of the perpendicular drawn from a point P(3, 4, 5) on the xy-plane. The coordinates of point L are
(a)    (3,0,0)
(b)    (0,4,5)
(c)     (3, 0, 5)
(d)    none of these
Sol: (d) We know that on the xy-plane, z = 0.
Hence, the coordinates of the points L are (3,4, 0).

Q34. L is the foot of the perpendicular drawn from a point (3, 4, 5) on x-axis. The coordinates of L are
(a)    (3,0,0)
(b)    (0,4,0)
(c)     (0, 0, 5)
(d)    none of these
Sol: (a) On the x-axis, y = 0 and z = 0.
Hence, the required coordinates are (3, 0,0).

Fill in the Blanks Type Questions
Q35. The three axes OX, OY, OZ determine______ .
Sol: The three axes OX, OY and OZ determine three coordinate planes.

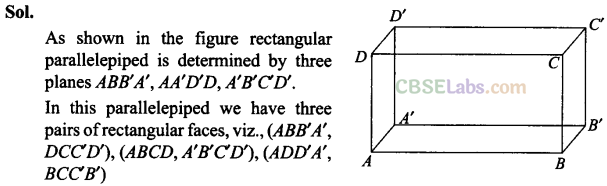
Q36. The three planes determine a rectangular parallelepiped which has____ of rectangular faces.

Q37. The coordinates of a point are the perpendicular distance from the _____ on the respective axes.
Sol: Given points

Q38. The three coordinate planes divide the space into _________parts.
Sol: Eight

Q39. If a point P lies in yz-plane, then the coordinates of a point on yz-plane is of the form_______.
Sol: We know that, on yz-plane, x = 0.So, the coordinates of the required point are (0, y, z).

Q40. The equation of yz-plane is ______ .
Sol: On yz-plane for any point x-coordinate is zero.
So, yz-plane is locus of point such that x = 0, which is its equation.

Q41. If the point P lies on z-axis, then coordinates of P are of the form_____.
Sol: On the z-axis, x = 0 and y = 0.
So, the required coordinates are of the form (0, 0, z).

Q42. The equation of z-axis, are ______.
Sol: Any point on the z-axis is taken as (0, 0, z).
So, for any point on z-axis, we have x = 0 and y = 0, which together represents its equation.
Q43. A line is parallel to xy-plane if all the points on the line have equal_________.
Sol: A line is parallel to xy-plane if each point P(x, y, z) on it is at same distance from xy-plane.
Distance of point P from xy plane is ‘z’
So, line is parallel to xy-plane if all the points on the line have equal z-coordinate.

Q44. A line is parallel to x-axis if all the points on the line have equal ______.
Sol: A line is parallel to x-axis if each point on it maintains constant distance from y-axis and z-axis.
So, each point has equal y and z-coordinates. .

Q45. x = a represents a plane parallel to .
Sol: Locus of point P(x, y, z) is x = a.
Therefore, each point P has constant x-coordinate.
Now, x is distance of point P from yz-plane.
So, here plane x = a is at constant distance ‘a’ from yz-plane and parallel to _yz-plane.

Q46. The plane parallel to yz-plane is perpendicular to_____ .
Sol: The plane parallel to yz-plane is perpendicular to x-axis.

Q47. The length of the longest piece of a string that can be stretched straight in a  rectangular room whose dimensions are 10, 13 and 8 units are______ .
Sol: Given dimensions are: a = 10, 6=13 andc = 8.
Required length of the string = yja ² + b ² + c ² = ^100 + 169 + 64 = -7333

Q48. If the distance between the points (a, 2,1) and (1,-1,1) is 5, then a_______ .
Sol: Given points are (a, 2,1) and (1,-1,1).

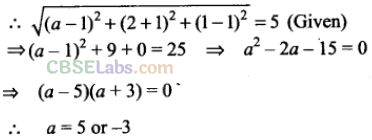
Q49. If the mid-points of the sides of a triangle AB; BC; CA are D(l, 2, – 3), E( 3, 0, 1) and F(-l, 1, -4), then the centroid of the triangle ABC is________ .
Sol: Given that, mid-points of sides of AABC are D( 1, 2, -3), E(3, 0, 1) and F(-l, 1,-4).

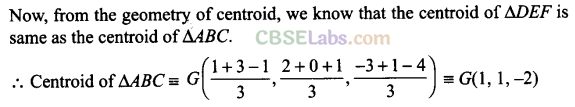
Matching Column Type Questions

Q50. Match each item given under the column C ₁ to its correct answer given under column C ₂ .

Column C,		Column C 2
(a)	In xy-plane	(i)	1st octant
(b)	Point (2, 3,4) lies in the	(ii)	vz-plane
(c)	Locus of the points having x coordinate 0 is	(iii)	z-coordinate is zero
(d)	A line is parallel to x-axis if and only	(iv)	z-axis                      .
(e)	If x = 0, y = 0 taken together will represent the	(v)	plane parallel to xy-plane
(f)	z = c represent the plane	(vi)	if all the points on the line have equal y and z-coordinates.
(g)	Planes x = a, y = b represent the line	(vii)	from the point on the respective axis.
00	Coordinates of a point are the distances from the origin to the feet of perpendiculars	(viii)	parallel to z-axis
(i)	A ball is the solid region in the space	(ix)	disc
G)	Region in the plane enclosed by a circle is known as a	00	sphere

Sol: (a) In xy-plane, z-coordinate is zero.
(b) The point (2, 3,4) lies in 1st octant.
(c) Locus of the points having x-coordinate zero is yz-plane.
(d) A line is parallel to x-axis if and only if all the points on the line have equal y and z-coordinates.
(e)x = 0, y = 0 represent z-axis
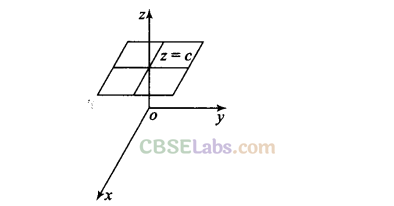
(f) z = c represents the plane parallel to xy-plane.

(g) The plane x = a is parallel to yz-plane.
Plane y = b is parallel to xz-plane.
So,    planes x = a and y = b is line of intersection of these planes.
Now, line of intersection of yz-plane and xz-plane is z-axis.
So, line of intersection of planes x = a andy = b is line parallel to z-axis.
(h) Coordinates of a point are the distances from the origin to the feet of perpendicular from the point on the respective axis.
(i) A ball is the solid region in the space enclosed by a sphere.
(j) The region in the plane enclosed by a circle is known as a disc.
Hence, the correct matches are:
(a) – (iii), (b) – (i), (c) – (ii), (d) – (vi), (e) – (iv),
(f) – (v), (g) – (viii), (h) – (vii), (i) – (x), (j) – (ix),

LearnCBSE Online