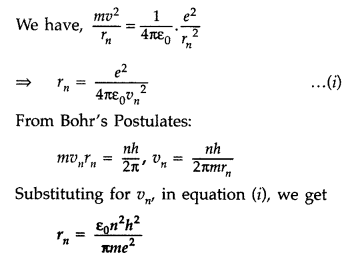Important Questions for Class 12 Physics Chapter 12 Atoms Class 12 Important Questions
Atoms Class 12 Important Questions Very Short Answer Type
Question 1.
Define ionisation energy. What is its value for a hydrogen atom? (All India 2010)
Answer:
Ionisation energy : The energy required to knock out an electron from an atom is called ionisation energy of the atom.
For hydrogen atom it is 13.6 eV.
Question 2.
Write the expression for Bohr’s radius in hydrogen atom. (Delhi 2010)
Answer:
Bohr’s radius in hydrogen atom,
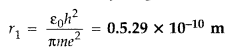
Question 3.
What is the ratio of radii of the orbits corresponding to first excited state and ground state in a hydrogen atom? (Delhi 2010)
Answer:

Question 4.
The radius of innermost electron orbit of a hydrogen atom is 5.3 × 10
-11
m. What is the radius of orbit in the second excited state? (Delhi 2011)
Answer:
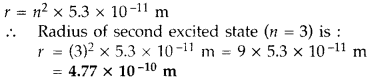
Question 5.
Find the ratio of energies of photons produced due to transition of an electron of hydrogen atom from its
(i) second permitted energy level to the first level, and
(ii) the highest permitted energy level to the first permitted level. (All India 2010)
Answer:
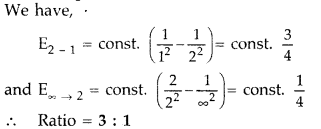
Question 6.
The ground state energy of hydrogen atom is -13.6 eV. What are the kinetic and potential energies of electron in this state? (All India)
Answer:
Kinetic energy, K
e
= + T.E. = 13.6 eV
Potential energy, P
e
= 2 T.E. = 2 (-13.6) = – 27.2 eV
Question 7.
Why is the classical (Rutherford) model for an atom—of electron orbitting around the nucleus—not able to explain the atomic structure? (All India 2012)
Answer:
As the revolving electron loses energy continuously, it must spiral inwards and eventually fall into the nucleus. So it was not able to explain the atomic structure.
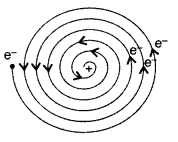
Question 8.
When is Ha line of the Balmer series in the emission spectrum of hydrogen atom obtained? (Comptt. Delhi 2012)
Answer:
Balmer series is obtained when an electron jumps to the second orbit (n
1
= 2) from any orbit n
2
= n > 2 .
Question 9.
What is the maximum number of spectral lines emitted by a hydrogen atom when it is in the third excited state? (Comptt. All India 2012)
Answer:
For third excited state, n
2
= 4, and n
1
= 3, 2, 1 Hence there are 3 spectral lines.
Atoms Class 12 Important Questions Short Answer Type SA-I
Question 10.
(i) In hydrogen atom, an electron undergoes transition from 2nd excited state to the first excited state and then to the ground state. Identify the spectral series to which these transitions belong.
(ii) Find out the ratio of the wavelengths of the emitted radiations in the two cases. (Comptt. All India 2012)
Answer:

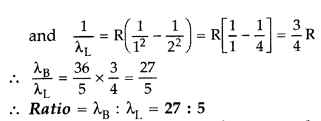
Question 11.
(i) In hydrogen atom, an electron undergoes transition from third excited state to the second excited state and then to the first excited state. Identify the spectral series to which these transitions belong.
(ii) Find out the ratio of the wavelengths of the emitted radiations in the two cases. (Comptt. All India 2012)
Answer:

Question 12.
In hydrogen atom, an electron undergoes transition from 3rd excited state to the first excited state and then to the ground state. Identify the spectral series to which these transitions belong.
(ii) Find out the ratio of the wavelengths of the emitted radiations in the two cases. (Comptt. All India 2012) Answer:
(i) These transitions belong to :
1. Balmer series,
2. Lyman series
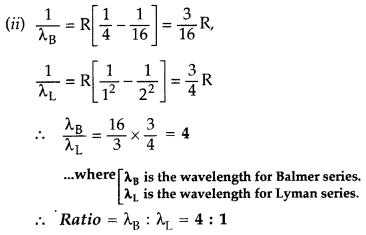
Question 13.
Using Rutherford model of the atom, derive the expression for the total energy of the electron in hydrogen atom. What is the significance of total negative energy possessed by the electron? (All India 2012)
Answer:
Expression for total energy of electron in H-atom using Rutherford model : As per Rutherford model of atom, centripetal force (F
c
) required to keep electron revolving in orbit is provided by the electrostatic force (Fe) of attraction between the revolving electron and nucleus.
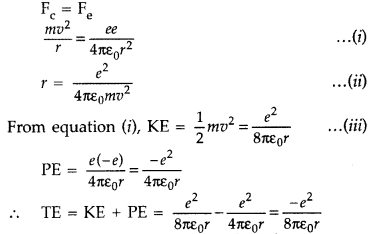
The negative sign indicates that the revolving electron is bound to the positive nucleus.
Question 14.
Using Bohr’s postulates of the atomic model, derive the expression for radius of nth electron orbit. Hence obtain the expression for Bohr’s radius. (All India 2012)
Answer:
Basic postulates of Bohr’s atomic model:
(i) Every atom consists of a central core called nucleus in which entire positive charge and mass of the atom are concentrated. A suitable number of electrons revolve around the nucleus in circular orbit. The centripetal force required for revolution is provided by the electrostatic force of attraction between the electron and the nucleus.
(ii) Electron can resolve only in certain discrete non-radiating orbits, called stationary orbit. Total angular momentum of the revolving electron in an integral multiple of h/2π.
… where [h is plank constant]
![]()
(iii) The radiation of energy occurs only when an electron jumps from one permitted orbit to another. The difference in the total energy of electron in the two permitted orbit is absorbed when the electron jumps from inner to the outer orbit and emitted when electron jumps from outer to inner orbit.
Radii of Bohr’s stationary orbits. According to Bohr’s postulates, angular momentum of electron for any permitted orbit is,
![]()
Also, according to Bohr’s postulates, the centripetal force is equal to electrostatic force between the electron and nucleus.
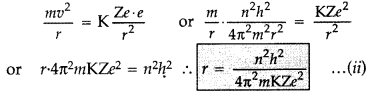

Question 15.
Show that the radius of the orbit in hydrogen atom varies as n
2
, where n is the principal quantum number of the atom. (Delhi 2012)
Answer:
When an electron moves around hydrogen nucleus, the electrostatic force between electron and hydrogen nucleus provides necessary centrepetal force.
![]()
Also we know from Bohr’s postulate,
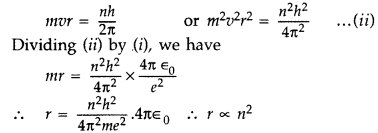
Question 16.
When an electron in hydrogen atom jumps from the third excited state to the ground state, how would the de Broglie wavelength associated with the electron change? Justify your answer. (All India 2012)
Answer:
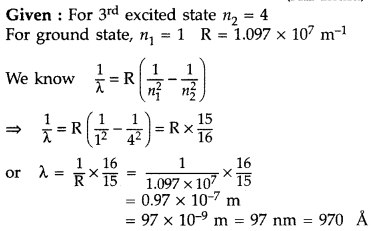
It lies in the ultra-violet region.
Question 17.
Calculate the shortest wavelength in the Balmer series of hydrogen atom. In which region (infra-red, visible, ultraviolet) of hydrogen spectrum does this wavelength lie? (All India 2012)
Answer:
In Balmer series, an electron jumps from higher orbits to the second stationary orbit (n
f
= 2). Thus for this series :
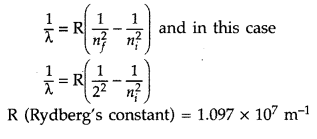
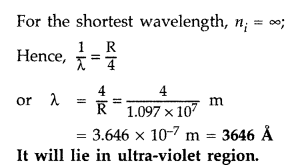
Question 18.
The figure shows energy level diagram of hydogen atom
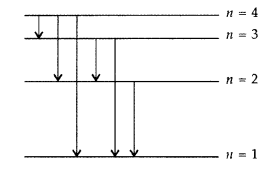
(a) Find out the transition which results in the emission of a photon of wavelength 496 nm.
(b) Which transition corresponds to the emission of radiation of maximum wavelength? Justify your answer. (Comptt. All India 2012)
Answer:
(a) Transition emitting wavelength λ = 496 nm The given wavelength lies in visible region (Balmer series) when,
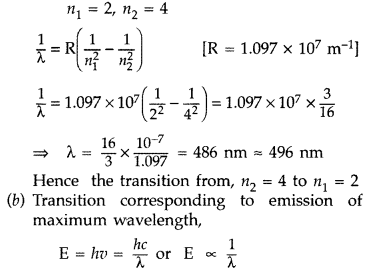
which means that the maximum wavelength emmission will be there when the energy level difference is minimum. From the given energy level diagram, it corresponds to :
![]()
Question 19.
In Rutherford scattering experiment, draw the trajectory traced by a-particles in the coulomb field of target nucleus and explain how this led to estimate the size of the nucleus. (Comptt. All India 2012)
Answer:
Note: The Rutherford scattering experiment is also known as the Geiger Marsden experiment.
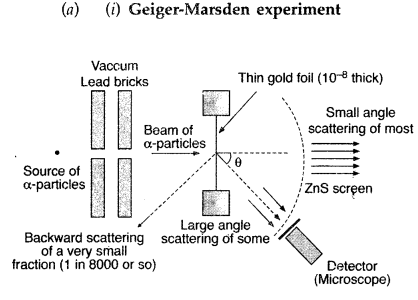
(ii) For most of the α-particles, impact parameter is large, hence they suffer very small repulsion due to nucleus and go right through the foil.
(iii) Trajectory of α-particles
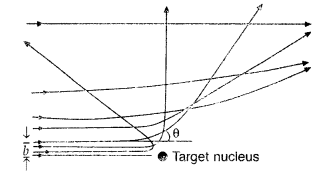
It gives an estimate of the size of nucleus, that it relatively very very small as compared to the size of atom.
Question 20.
Define ionization energy.
How would the ionization energy change when electron in hydrogen atom is replaced by a particle of mass 200 times that of the electron but having the same charge? (All India 2016)
Answer:
Definition of ionization energy : “The minimum energy, required to free the electron from the ground state of the hydrogen atom, is known as Ionization Energy.”
The ionization energy is given by :
![]()
∴Ionization Energy will become 200 times,
∵ the mass of given particle is 200 times.
Question 21.
Calculate the shortest wavelength of the spectral lines emitted in Balmer series.
[Given Rydberg constant, R = 10
7
m
-1
] (All India 2016)
Answer:

Question 22.
The electron, in a hydrogen atom, is in its second excited state.
Calculate the wavelength of the lines in the Lyman series, that can be emitted through the permissible transitions of this electron.
(Given the value of Rydberg constant, R = 1.1 × 107 m
-1
) (Comptt. Delhi 2016)
Answer:
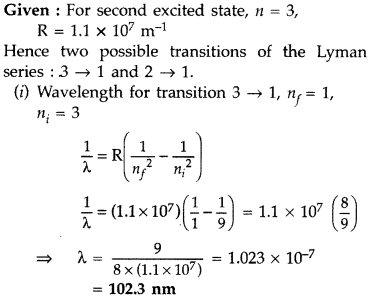
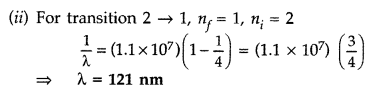
Question 23.
An α-particle moving with initial kinetic energy K towards a nucleus of atomic number z approaches a distance ‘d’ at which it reverses its direction. Obtain the expression for the distance of closest approach ‘d’ in terms of the kinetic energy of α-particle K. (Comptt. All India 2016)
Answer:

Question 24.
Find the ratio between the wavelengths of the ‘most energetic’ spectral lines in the Balmer and Paschen series of the hydrogen spectrum. (Comptt. All India 2016)
Answer:
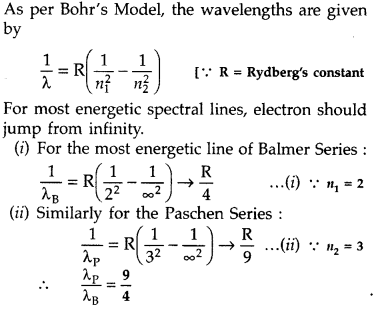
Question 25.
Define the distance of closest approach. An a-particle of kinetic energy ‘K’ is bombarded on a thin gold foil. The distance of the closest approach is V. What will be the distance of closest approach for an a-particle of double the kinetic energy? (Delhi 2016)
Answer:
The distance of closest approach is defined as “the distance of charged particle from the centre of the nucleus, at which the whole of the initial kinetic energy of the (far off) charged particle gets converted into the electric potential energy of the system”.
Distance of closest approach (r
c
) is given by
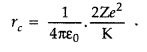
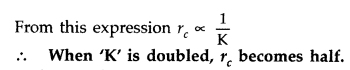
Question 26.
Write two important limitations of Rutherford nuclear model of the atom. (Delhi 2016)
Answer:
Important limitations of Rutherford Model :
- According to Rutherford model, electron orbiting around the nucleus, continuously radiates energy due to the acceleration; hence the atom will not remain stable.
- As electron spirals inwards; its angular velocity and frequency change continuously; therefore it. will emit a continuous spectrum.
Question 27.
Find out the wavelength of the electron orbiting in the ground state of hydrogen atom. (Delhi 2016)
Answer:
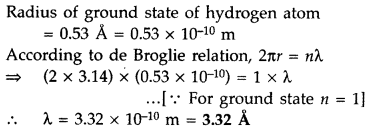
Question 28.
Find the wavelength of the electron orbiting in the first excited state in hydrogen atom. (Delhi 2016)
Answer:
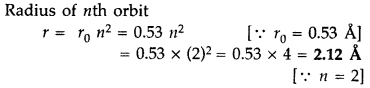
Question 29.
A 12.5 eV electron beam is used to excite a gaseous hydrogen atom at room temperature. Determine the wavelengths and the corresponding series of the lines emitted. (All India 2016)
Answer:

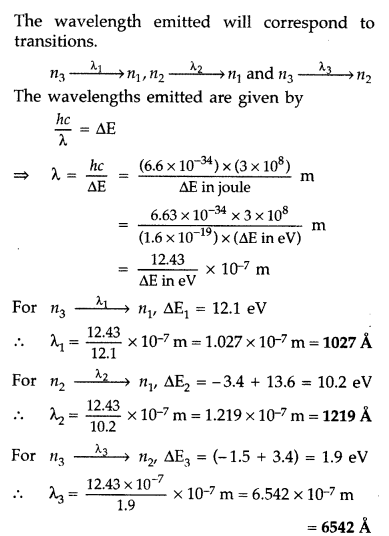
Question 30.
The short wavelength limit for the Lyman series of the hydrogen spectrum is 913.4 A Calculate the short wavelength limit for Balmer series of the hydrogen spectrum. (All India 2016)
Answer:
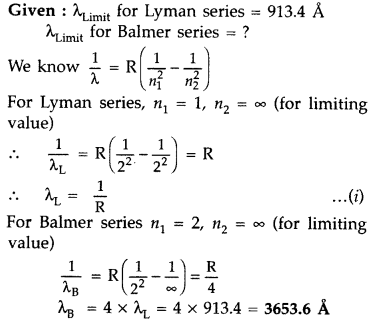
Question 31.
The ground state energy of hydrogen atom is -13.6 eV. If an electron makes a transition from an energy level -1.51 eV to -3.4 eV, calculate the wavelength of the spectral line emitted and name the series of hydrogen spectrum to which it belongs. (All India 2016)
Answer:
![]()
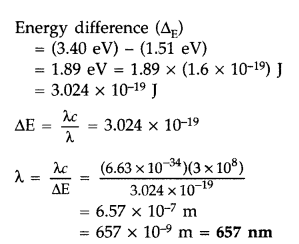
Question 32.
Calculate the shortest wavelength of light emitted in the Paschen series of hydrogen spectrum. Which part of the electromagnetic spectrum, does it belong to ? (Given : Rydberg constant, R = 1.1 × 10
7
m
-1
) (Comptt. Delhi 2016)
Answer:
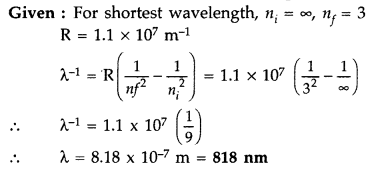
It belongs to the Infrared part of the spectrum.
Question 33.
Calculate the shortest wavelength of photons emitted in the Bracket series of hydrogen spectrum. Which part of the e.m. spectrum, does it belong? [Given Rydberg constant, R = 1.1 × 10
7
m
-1
] (Comptt. Delhi 2016)
Answer:
In bracket series, n
f
= 4

Question 34.
Calculate the longest wavelength of the photons emitted in the Balmer series of hydrogen spectrum. Which part of the e.m. spectrum, does it belong to?
[Given Rydberg constant, R = 1.1 × 107 m
-1
]. (Comptt. Delhi 2016)
Answer:
Balmer series is produced when an electron jumps from higher orbits to second stationary orbit (n
f
= 2).
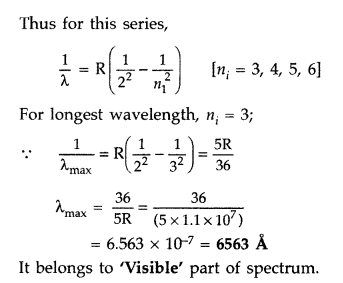
Atoms Class 12 Important Questions Short Answer Type SA-II
Question 35.
The energy level diagram of an element is given. Identify, by doing necessary calculations, which transition corresponds to the emission of a spectral line of wavelength 102.7 nm. (Delhi 2008)
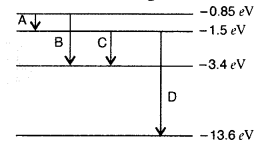
Answer:
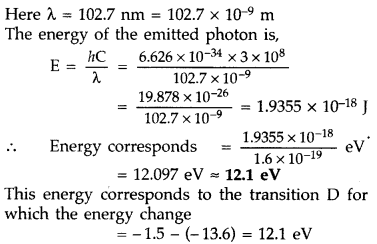
Question 36.
The ground state energy of hydrogen atom is -13.6 eV.
(i) What is the kinetic energy of an electron in the 2
nd
excited state?
(ii) If the electron jumps to the ground state from the 2
nd
excited state, calculate the wavelength of the spectral line emitted. (All India 2008)
Answer:
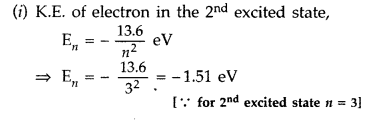
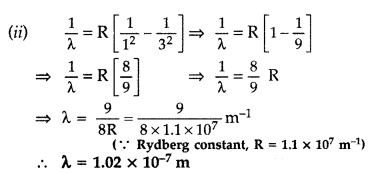
Question 37.
The ground state energy of hydrogen atom is -13.6 eV.
(i) What is the potential energy of an electron in the 3
rd
excited state?
(ii) If the electron jumps to the ground state from the 3
rd
excited state, calculate the wavelength of the photon emitted. (All India 2008)
Answer:

Question 38.
(a) The energy levels of an atom are as shown here. Which of them will result in the transition of a photon of wavelength 275 nm?
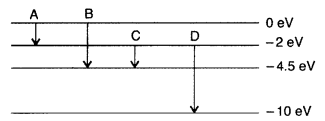
(b) Which transition corresponds to emission of radiation of maximum wavelength? (Delhi 2008)
Answer:


Question 39.
The energy levels of a hypothetical atom are shown below. Which of the shown transitions will result in the emission of a photon of wavelength 275 nm? Which of these transitions correspond to emission of radiation of
(i) maximum and
(ii) minimum wavelength ?
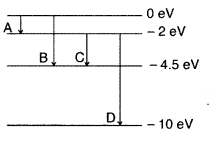
(Delhi 2011)
Answer:

Question 40.
(a) Using Bohr’s second postulate of quantization of orbital angular momentum show that the circumference of the electron in the n,h orbital state in hydrogen atom is n times the de-Broglie wavelength associated with it.
(b) The electron in hydrogen atom is initially in the third excited state. What is the maximum number of spectral lines which can be emitted when it finally moves to the ground state? (Delhi 2012)
Answer:
(a) According to the de-Broglie hypothesis, this electron is also associated with wave character.
Hence a circular orbit can be taken to be a stationary energy state only if it contains an integral number of de- Broglie wavelengths i.e. we must have
2πr = nλ
According to Bohr’s-second postulate
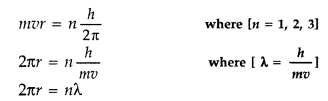
Hence the circumference of the electron in the n
th
orbital state in hydrogen atom is n times the de-Broglie wavelength associated with it.
(b) For third excited state n = 4
For ground state n = 1
Hence, possible transitions are :
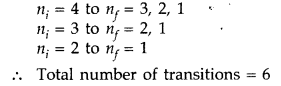
Question 41.
In a Geiger-Marsden experiment, calculate the distance of closest approach to the nucleus of Z = 80, when an α-particle of 8 MeV energy impinges on it before it comes momentarily to rest and reverses its direction.
How will the distance of closest approach be affected when the kinetic energy of the α-particle is doubled? (All India 2012)
Answer:
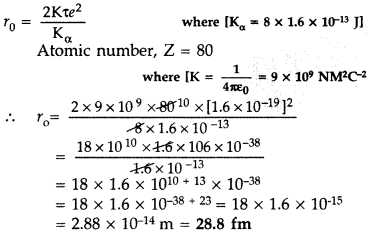
When kinetic energy of a-particle is doubled, then distance of closest approach becomes half

Question 42.
The ground state energy of hydrogen atom is -13.6 eV. If an electron makes a transition from an energy level -0.85 eV to -3.4 eV, calculate the wavelength of the spectral line emitted. To which series of hydrogen spectrum does this wavelength belong? (All India 2012)
Answer:

(ii) This wavelength belongs to Balmer series of hydrogen spectrum.
Question 43.
Using Bohr’s postulates, obtain the expression for the total energy of the electron in the stationary states of the hydrogen atom. Hence draw the energy level diagram showing how the line spectra corresponding to Balmer series occur due to transition between energy levels. (Delhi 2012)
Answer:

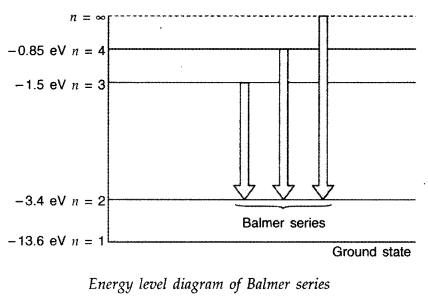
Question 44.
Using Bohr’s postulates, obtain the expressions for
(i) kinetic energy and
(ii) potential energy of the electron in stationary state of hydrogen atom. Draw the energy level diagram showing how the transitions between energy levels result in the appearance of Lyman Series. (Delhi 2012)
Answer:

Question 45.
In the ground state of hydrogen atom, its Bohr radius is given as 5.3 × 10
-11
m. The atom is excited such that the radius becomes 21.2 × 10
-11
m. Find
(i) the value of the principal quantum number and
(ii) the total energy of the atom in this excited state. (Comptt. Delhi 2012)
Answer:
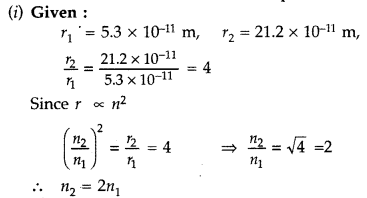
Therefore, Value of principal quantum number in this excited state is 2.
(ii) Energy of electron in ground state = -13.6 eV
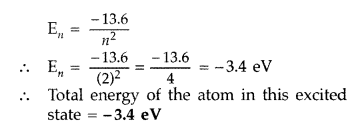
Question 46.
A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited? Calculate the wavelengths of the first member of Lyman and first member of Balmer series. (Delhi 2014)
Answer:

Hydrogen atom will be excited upto third energy level, because energy of electron is less than that of 4
th
energy level.
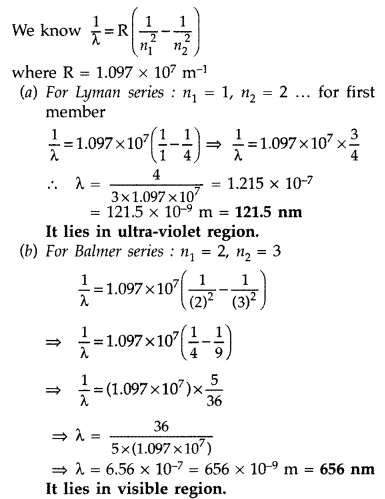
Question 47.
A 12.9 eV beam of electrons is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited?
Calculate the wavelength of the first member of Paschen series and first member of Balmer series. (Delhi 2014)
Answer:
1st part: Similar to Q. 46, Page 280
Wavelength of the first member of Paschen series: n
1
= 3, n
2
= 4
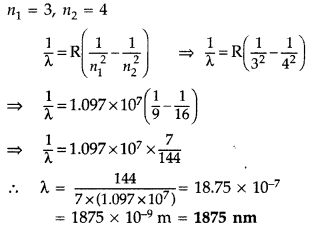
It lies in infra-red region.
Question 48.
A 12.3 eV electron beam is used to bombard gaseous hydrogen at room temperature. Upto which energy level the hydrogen atoms would be excited?
Calculate the wavelengths of the second member of Lyman series and second member of Balmer series. (Delhi 2014)
Answer:
1st part: Similar to Q. 46, Page 280
(i) Wavelength of second member of Lyman series : n
1
= 1, n
2
= 3
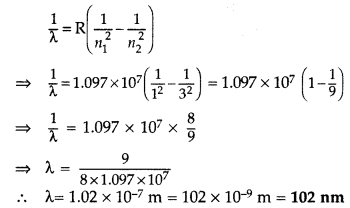
∴ It lies in ultra violet region.
(ii) Wavelength of second member of Balmer series (n
1
= 2, n
2
= 4)
It lies in visible region.
Question 49.
(a) The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10
-11
m. Calculate its radius in n = 3 orbit.
(b) The total energy of an electron in the first excited state of the hydrogen atom is -3.4 eV. Find out its
(i) kinetic energy and
(ii) potential energy in this state. (Comptt. Delhi 2014)
Answer:

Question 50.
(a) The radius of the innermost electron orbit of a hydrogen atom is 5.3 × 10
11
m. Calculate its radius in n = 2 orbit.
(b) The total energy of an electron in the second excited state of the hydrogen atom is -1.51 eV. Find out its
(i) kinetic energy and
(ii) potential energy in this state. (Comptt. Delhi 2014)
Answer:
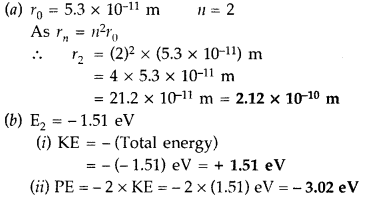
Question 51.
(a) The orbital radius of the electron in the first excited state of hydrogen atom is 21.2 × 10
-11
m. Find out its radius in the second excited state.
(b) The total energy of the electron in the ground state is -13.6 eV. Find out
(i) its. kinetic energy and
(ii) potential energy in the first excited state. (Comptt. Delhi 2014)
Answer:
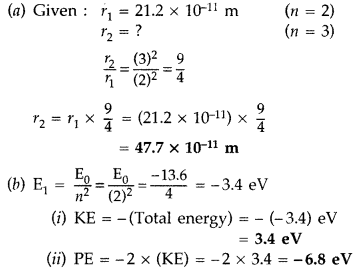
Question 52.
The value of a ground state energy of hydrogen atom is -13.6 eV.
(i) Find the energy required to move an electron from the ground state to the first excited state of the atom.
(ii) Determine
(a) the kinetic energy and
(b) orbital radius in the first excited state of the atom. (Given the value of Bohr radius = 0.53 Å) (Comptt. All India 2014)
Answer:
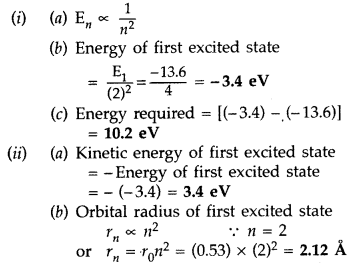
Question 53.
The value of ground state energy of hydogen atom is -13.6 eV and Bohr radius is 0.53Å. Calculate
(i) the energy required to move an electron from the ground state to the second excited state.
(ii) (a) the kinetic energy and
(b) the orbital radius in the second excited state of the atom. (Comptt. All India 2014)
Answer:
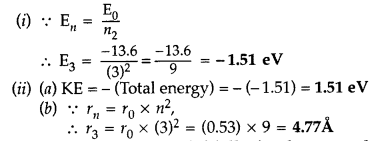
Question 54.
(i) A hydrogen atom initially in the ground state absorbs a photon which excites it to the n- 4 level. Determine the wavelength of the photon.
(ii) The radius of innermost electron orbit of a hydrogen atom is 5.3 × 10
-11
m. Determine its radius in n = 4 orbit.(Comptt. All India 2014)
Answer:

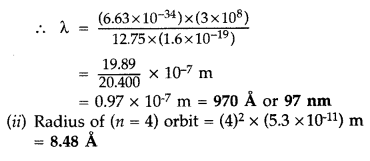
Question 55.
In the study of Geiger-Marsdon experiment on scattering of a particles by a thin foil of gold, draw the trajectory of a-particles in the coulomb field of target nucleus. Explain briefly how one gets the information on the size of the nucleus from this study.
From the relation, R = R
0
\(\mathbf{A}^{1 / 3}\), where R
0
, is constant and A is the mass number of the nucleus, show that nuclear matter density is independent of A. (Delhi 2015)
Answer:
(i) Trajectory of α-particles
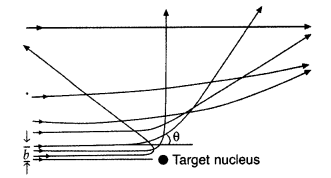
(ii) Size of nucleus : Only a small fraction of the incident a-particles rebound. This shows that the mass of the atom is concentrated in a small volume in the form of nucleus and gives an idea of the size of nucleus.

Question 56.
(i) State Bohr’s quantization condition for defining stationary orbits. How does de-Broglie hypothesis explain the stationary orbits?
(ii) Find the relation between the three wave-lengths λ
1
, λ
2
and λ
3
from the energy level diagram shown below: (Delhi 2016)
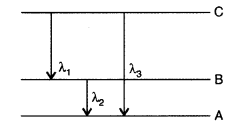
Answer:

Question 57.
Using Bohr’s postulates, derive the expression for the total energy of the electron revolving in n
th
orbit of hydrogen atom. Find the wavelength of H line, given value of Ryderg constant, R = 1.1 × 10
7
m
-1
.
Answer:
For total energy of the electron orbiting in n
th
orbit :
Total energy of electron in Bohr’s stationary orbit K.E. which is due to velocity and P.E. due to position of electron
From the first postulate of Bohr’s atom modal

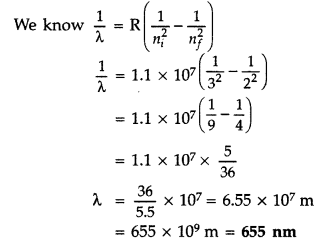
Atoms Class 12 Important Questions Long Answer Type
Question 58.
Draw a schematic arrangement of the Geiger-Marsden experiment. How did the scattering of α-particles by a thin foil of gold provide an important way to determine an upper limit on the size of the nucleus? Explain briefly.
(All India 2009)
Answer:
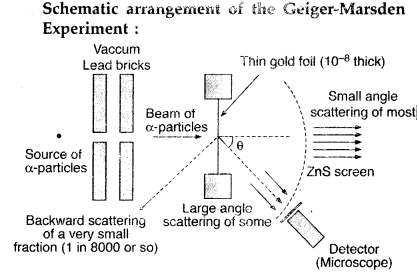
(i) Beam of α-particles get deviated at various angles with different probabilities.
(ii) α-particles with least impact parameter suffers larger scattering – rebounding on head on collision.
(iii) For larger impact parameter, the particle remains almost undeviated.
Explanation:
The fact that the number of incident particles rebounding back is only a small of fraction, means that numer of α-particles headon collision is small. This implies that the entire positive charge of the atom is concentrated in a small volume. This confirms that the nucleus of the atom has an apper size limit.
Question 59.
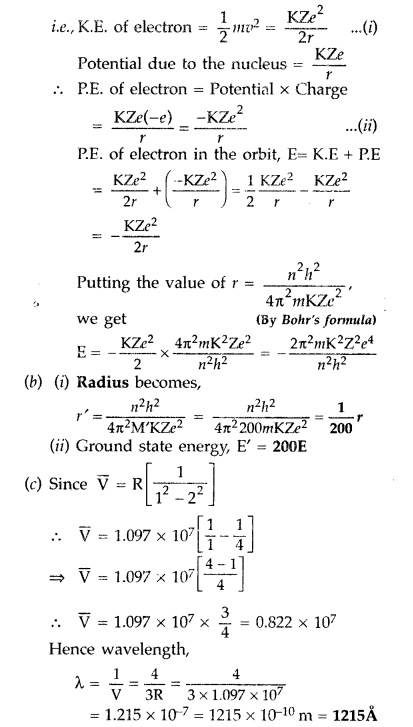
(a) Using Bohr’s theory of hydrogen atom, derive the expression for the total energy of the electron in the stationary states of the atom.
(b) If electron in the atom is replaced by a particle (muon) having the same charge but mass about 200 times as that of the electron to form a muonic atom, how would
(i) the radius and
(ii) the ground state energy of this be affected?
(c) Calculate the wavelength of the first spectral line in the corresponding Lyman series of this atom. (Comptt. Delhi 2012)
Answer:
(a) Total energy of electron in Bohr’s stationary orbit—K.E which is due to velocity and P.E. due to position of electron.
From the first postulate of Bohr’s atom model,
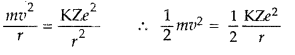
Question 60.
Using Bohr’s postulates, derive the expression for the frequency of radiation emitted when electron in hydrogen atom undergoes transition from higher energy state (quantum number n
i
) to the lower state (n
f
).
When electron in hydrogen atom jumps from energy state n
i
= 4 to n
f
= 3, 2, 1, identify the spectral series to which the emission lines belong. (All India 2013)
Answer:
When a hydrogen atom receives energy by process such as electron collisions of heat, the atom may acquire sufficient energy to raise the electron to higher energy states from n = 1 to n = 2, it is said to be in an excited state. When an electron falls back from excited state to lower energy state by emitting, there is a photon of particular energy and of particular frequency.
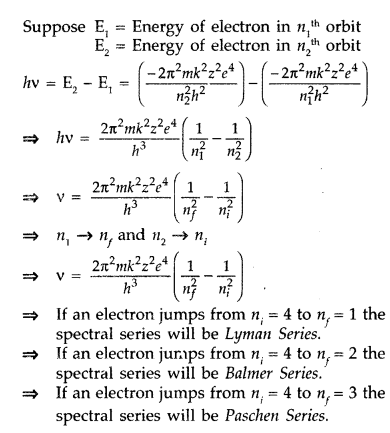
Question 61.
(a) Draw a schematic arrangement of Geiger- Marsden experiment showing the scattering of a-particles by a thin foil of gold. Why is it that most of the a-particles go right through the foil and only a small fraction gets scattered at large angles?
Draw the trajectory of the a-particle in the coulomb field of a nucleus. What is the significance of impact parameter and what information can be obtained regarding the size of the nucleus?
(b) Estimate the distance of closest approach to the nucleus (Z = 80) if a 7.7 MeV a-particle before it comes momentarily to rest and reverses its direction. (Comptt. Delhi 2015)
Answer:

(ii) For most of the α-particles, impact parameter is large, hence they suffer very small repulsion due to nucleus and go right through the foil.
(iii) Trajectory of α-particles

It gives an estimate of the size of nucleus, that it relatively very very small as compared to the size of atom.
(b) K.E. of the a-particle = Potential energy possessed by beam at distance of closest approach.
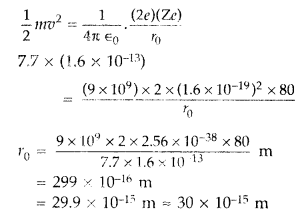
Question 62.
(a) Write two important limitations of Rutherford model which could not explain the observed features of atomic spectra. How were these explained in Bohr’s model. of hydrogen atom?
Use the Rydberg formula to calculate the wavelength of the H
α
line.
(Take R = 1.1 × 10
7
m
-1
).
(b) Using Bohr’s postulates, obtain the expression for the radius of the n
th
orbit in hydrogen atom. (Comptt. Delhi 2015)
Answer:
(a) Limitations of Rutherford Model :
(i) Electrons moving in a circular orbit around the nucleus would get, accelerated, therefore it would spiral into the nucleus, as it looses its energy.
(ii) It must emit a continuous spectrum.
Explanation according to Bohr’s model of hydrogen atom :
(i) Electron in an atom can revolve in certain stable orbits without the emission of radiant energy.
(ii) Energy is released/absorbed only, when an electron jumps from one stable orbit to another stable orbit. This results in a discrete spectrum.
Wavelength of H
α
line :
H
α
line is formed when an electron jumps from n
f
= 3 to n
i
= 2 orbit. It is the Balmer series
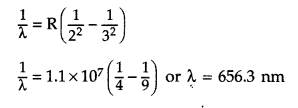
(b) Radius of n
th
orbit