Important Questions for Class 12 Physics Chapter 10 Wave Optics Class 12 Important Questions
Wave Optics Class 12 Important Questions Very Short Answer Type
Question 1.
How does the fringe width of interference fringes change, when the whole apparatus of Young’s experiment is kept in a liquid of refractive index 1.3? (Delhi 2008)
Answer:
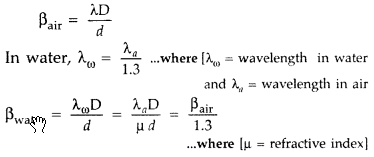
Fringe width becomes yL times of its initial value.
Question 2.
How does the angular separation of interference fringes change in Young’s experiment, if the distance between the slits is increased? (Delhi 2008)
Answer:
![]()
When separation between two slits is increased, angular separation decreases.
Question 3.
State the reason, why two independent sources of light cannot be considered as coherent sources. (Delhi 2008)
Answer:
Two independent sources of light cannot be coherent. This is because light is emitted by individual atoms, when they return to ground state. Even the smallest source of light contains billions of atoms which obviously cannot emit light waves in the same phase.
Question 4.
How does the angle of minimum deviation of a glass prism vary, if the incident violet light is replaced with red light? (All India 2008)
Answer:
![]()
When incident violet light is replaced with red light, the angle of minimum deviation of a glass decreases.
Question 5.
If the angle between the pass axis of polarizer and the analyser is 45°, write the ratio of the intensities of original light and the transmitted light after passing through the analyser. (Delhi 2008)
Answer:

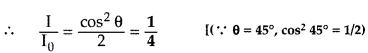
Question 6.
What type of wavefront will emerge from a
(i) point source, and
(ii) distant light source? (Delhi 2008)
Answer:
(i) Point source – Spherical wavefront
(ii) Distant light source – Plane wavefront.
Question 7.
Unpolarized light is incident on a plane surface of glass of refractive index µ at angle i. If the reflected light gets totally polarized, write the relation between the angle i and refractive index µ. (Delhi 2008)
Answer:
µ = tan i
p
.
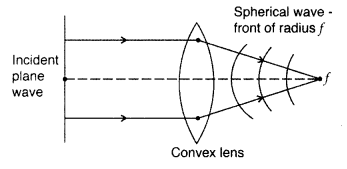
Question 8.
Draw a diagram to show refraction of a plane wave front incident in a convex lens and hence draw the refracted wave front. (Delhi 2008)
Answer:
Question 9.
At what angle of incidence should a light beam strike a glass slab of refractive index \(\sqrt{3}\), such that the reflected and the refracted rays are perpendicular to each other? (Delhi 2008)
Answer:
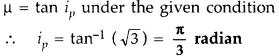
Question 10.
Differentiate between a ray and a wave front. (Delhi 2008)
Answer:
Ray defines the path of light.
Wave front is the locus of points in the light wave’ having the same phase of oscillation at any instant.
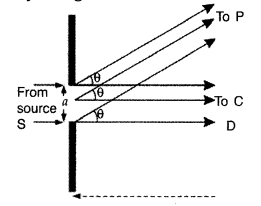
Question 11.
How would the angular separation of interference fringes in Young’s double slit experiment change when the distance between the slits and screen is doubled? (All India 2008)
Answer:
Angular separation \(\theta=\frac{\lambda}{d}\) and is independent of slit-screen separation
∴ There will be no change
Question 12.
How does the angular separation between fringes in single-slit diffraction experiment change when the distance of separation between the slit and screen is doubled? (All India 2012)
Answer:
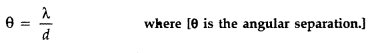
When the distance D of seperation between the slits and the screen is doubled, the angular seperation θ remains unchanged.
Question 13.
In a single-slit diffraction experiment, the width of the slit is made double the original width. How does this affect the size and intensity of the central diffraction band. (All India 2012)
Answer:
If the width of the diffraction slit is doubled, the size of the central diffraction band will become half and its intensity will become four times of its original value.
Question 14.
How does the fringe width, in Young’s double-slit experiment, change when the distance of separation between the slits and screen is doubled? (All India 2012)
Answer:
If the distance between slits and screen (D) is doubled, the fringe width in double slit
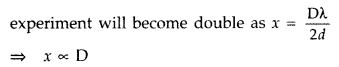
Question 15.
In what way is plane polarized light different from an unpolarized light? (Comptt. All India 2012)
Answer:
In case of polarized light, the directions of electric field vector are restricted to only a particular / plane whereas in an unpolarized light the direction of \(\overrightarrow{\mathrm{E}}\) is in all possible directions in a plane perpendicular to the direction of propagation.
Question 16.
In a single slit diffraction experiment, the width of the slit is reduced to half its original width. How would this affect the size and intensity of the central maximum? (Comptt. Delhi 2012)
Answer:
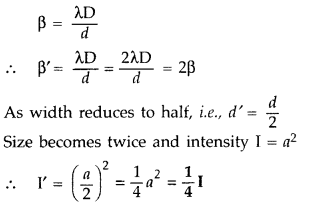
Question 17.
Which of the following waves can be polarized
(i) Heat waves
(ii) Sound waves? Give reason to support your answer. (Delhi 2013)
Answer:
Heat waves can be polarized as they are transverse in nature.
Question 18.
Define the term ‘coherent sources’ which are required to produce interference pattern in Young’s double slit experiment. (Comptt. Delhi 2014)
Answer:
Two monochromatic sources, which produce light waves, having a constant phase difference are defined as coherent sources.
Question 19.
Define the term ‘wavefront’.(Comptt. All India 2013)
Answer:
The wavefront is defined as the locus of all particles of a medium, which are vibrating in the same phase.
Question 20.
Draw the shape of the wavefront coming out of a convex lens when a plane wave is incident on it. (Comptt. All India 2013)
Answer:
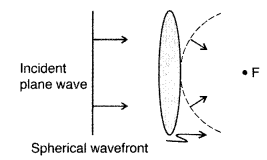
Question 21.
Draw the shape of the wavefront coming out of a concave mirror when a plane wave is incident on it. (Comptt. All India 2013)
Answer:
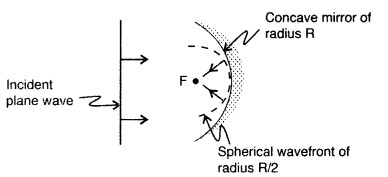
Question 22.
Why does Sun appear red at sunrise and sunset? (All India 2016)
Answer:
It is due to least scattering of red light as it has the longest wavelength.
[As per Rayleigh’s scattering, the amount of light
![]()
Question 23.
A beam of unpolarised light is incident, on the boundary between two transparent media, at an angle of incidence = i
B
, the Brewester’s angle. At what angle does the reflected light get polarised? (Comptt. All India 2016)
Answer:
At an angle of incidence = iB, the reflected light gets polarised.
Wave Optics Class 12 Important Questions Short Answer Type SA-I
Question 24.
State one feature by which the phenomenon of interference can be distinguished from that of diffraction.
A parallel beam of light of wavelength 600 nm is incident normally on a slit of width ‘a’. If the distance between the slits and the screen is 0.8 m and the distance of 2
nd
order maximum from the centre of the screen is. 15 mm, calculate the width of the slit. (All India 2008)
Answer:
(i) In interference all the maxima are of equal intensity.
In diffraction pattern central fringe is of maximum intensity while intensity of secondary maxima falls rapidly.

Question 25.
Define the term ‘linearly polarised light’. When does the intensity of transmitted light become maximum, when a polaroid sheet is rotated between two crossed polaroids? (All India 2008)
Answer:
Linearly polarised light is one in which the
vibration of light is present in one line only.
![]()
Intensity is maximum.
Question 26.
(i) State the principle on which the working of an optical fiber is based.
(ii) What are the necessary conditions for this phenomenon to occur? (All India 2009)
Answer:
(i) Working of an optical fibre is based on the principle of total internal reflection.
(ii) (a) Light should travel from a denser to rarer medium.
(b) Angle of incidence should be more than
![]()
Question 27.
(a) Why are coherent sources necessary to produce a sustained interference pattern?
(b) In Young’s double slit experiment using mono-chromatic light of wavelength X, the intensity of light at a point on the screen where path difference is X, is K units. Find out the intensity of light at a point where path difference is \(\frac{2 \lambda}{3}\). (Delhi 2012)
Answer:
(a) Coherent sources have a constant phase difference and, therefore, produce a sustained interference pattern.
These sources are needed to ensure that the position of maxima and minima do not change with time.
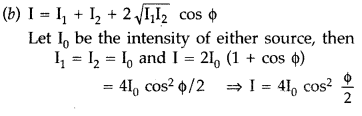
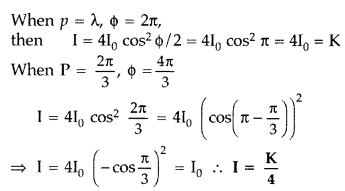
Question 28.
State two conditions required for obtaining co-herent sources.
In Young’s arrangement to produce interference pattern, show that dark and bright fringes appearing on the screen are equally spaced. (Comptt. Delhi 2009)
Answer:
Two conditions for obtaining coherent sources: (0 Two sources should give monochromatic light.
(ii) Coherent sources of light should be obtained from a single source by some device.
The fringe width (dark and bright) is given by
![]()
Hence, it is same for both dark and bright fringes So they are equally spaced on the screen.
Question 29.
Laser light of wavelength 640 nm incident on a pair of slits produces an interference pattern in which the bright fringes are separated by 7.2 mm. Calculate the wavelength of another source of light which produces interference fringes separated by 8.1 mm using same arrangement. Also find the minimum value of the order ‘n’ of bright fringe of shorter wavelength which coincides with that of the longer wavelength. (Comptt. All India 2012)
Answer:
Distance between two bright fringes = Fringe width
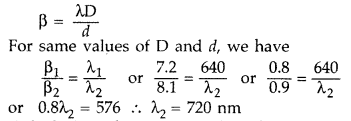
Calculation of minimum value of order: for n to be minimum
(n + 1)
th
maxima of shorter wavelength should coincide with n
th
maxima of longer wavelength
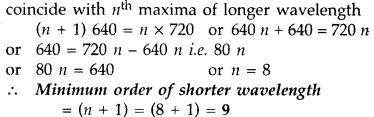
Question 30.
Yellow light (λ = 6000Å) illuminates a single slit of width 1 x 10-4 m. Calculate
(i) the distance between the two dark lines on either side of the central maximum, when the diffraction pattern is viewed on a screen kept 1.5 m away from the slit;
(ii) the angular spread of the first diffraction minimum. (Comptt. All India 2012)
Answer:
(i) Distance between two dark lines, on either
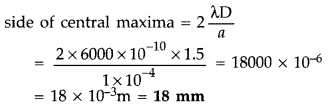
(ii) Angular spread of the first diffraction minimum (on either side)
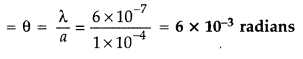
Question 31.
A parallel beam of light of 500 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1 m away. It is observed that the first minimum is at a distance of 2.5 mm from the centre of the screen. Calculate the width of the slit. (All India 2013)
Answer:

Question 32.
A parallel beam of light of 600 nm falls on a narrow slit and the resulting diffraction pattern is observed on a screen 1.2 m away. It is observed that the first minimum is at a distance of 3 mm from the centre of the screen. Calculate the width of the slit. (All India 2013)
Answer:

Question 33.
Write the distinguishing features between a diffraction pattern due to a single slit and the interference fringes produced in Young’s double slit experiment?
Answer:
Difference between interference and diffraction of light
| Interference | Diffraction | |
| 1. | Interference is due to superposition of two distinct waves coming from two coherent sources. | Diffraction is due to superposition of the secondary wavelets coming from different parts of the same wavefront. |
| 2. | Interference fringes may or may not be of the same width. | Diffraction fringes are not to be of the same width. |
| 3. | The intensity of minima is generally zero. | The intensity of minima is never zero. |
| 4. | All bright fringes are of uniform intensity. | All bright fringes are not of uniform intensity. |
Question 34.
Answer the following questions :
(i) In what way is diffraction from each slit related to the interference pattern in a double slit experiment?
(ii) When a tiny circular obstacle is placed in the path of light from a distance source, a bright spot is seen at the centre of the shadow of the obstacle. Explain, why. (Comptt. All India 2013)
Answer:
(i) Diffraction from each slit is related to interference pattern in a double slit experiment in the following ways :
- The intensity of minima for diffraction is never zero, while for interference it is generally zero.
- All bright fringes for diffraction are not of uniform intensity, while for interference, these are of uniform intensity
(ii) Waves from the distant source are diffracted by the edge of the circular obstacle and these diffracted waves interfere constructively at the centre of the obstacle’s shadow produc¬ing a bright spot.
Question 35.
(a) Write the conditions under which light sources can be said to be coherent.
(b) Why is it necessary to have coherent sources in order to produce an interference pattern? (Comptt. All India 2013)
Answer:
(a) Coherent sources of light. The sources of light, which emit continuously light waves of the same wavelength, same frequency and in same phase are called Coherent sources of light.
Interference pattern is not obtained. This is because phase difference between the light waves emitted from two different sodium lamps will change continuously.
(b) Conditions for interference. The important conditions for obtaining interference of light are :
- The two sources of light must be coherent. i.e. they should exist continuous waves of same wavelength or frequency.
- The two sources should be monochromatic.
- The phase difference of waves from two sources should be constant.
- The amplitude of waves from two sources should be equal.
- The coherent sources must be very close to each other.
Question 36.
(i) Monochromatic light of frequency 6.0 × 10
14
Hz is produced by a laser. The power emitted is 2.0 × 10
-3
W. Estimate the number of photons emitted per second on an average by the source.
(ii) Draw a plot showing the variation of photoelectric current versus the intensity of incident radiation on a given photosensitive surface. (Delhi 2014)
Answer:

Question 37.
For a single slit of width “a”, the first minimum of the interference pattern of a monochromatic light of wavelength λ occurs at an angle of \(\frac{\lambda}{a}\) .
At the same angle of \(\frac{\lambda}{a}\), we get a maximum for a two narrow slits separated by a distance “a”. Explain (Delhi 2014)
Answer:
For a single slit of width ‘a’,
the n
th
minimum, \(\sin \theta_{n}=\frac{n \lambda}{a}\)
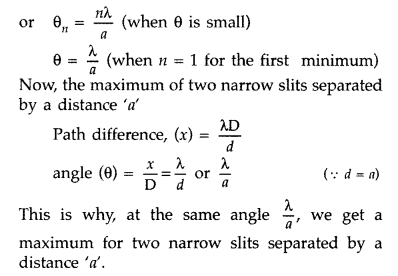
Question 38.
Find an expression for intensity of transmitted light when a polaroid sheet is rotated between two crossed polaroids. In which position of the Polaroid sheet will the transmitted intensity be maximum? (Delhi 2015)
Answer:
Let the rotating Polaroid sheet make an angle θ with the first polaroid.
∴ angle with the other polaroid will be (90 – θ)
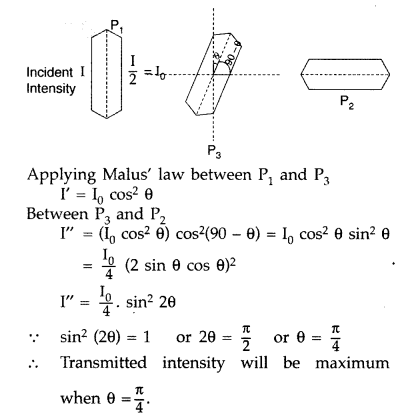
Question 39.
Distinguish between unpolarised and a linearly polarised light. Describe, with the help of a diagram, how unpolarised light gets linearly polarised by scattering. (Comptt. Delhi 2016)
Answer:
Unpolarized light : A light wave, in which the electric vector oscillates in all possible directions in a plane perpendicular to the direction of propagation is known as unpolarized light.
Linearly polarized light : If the oscillations of the electric vectors are restricted to just one direction, in a plane perpendicular to the direction of propagation, the corresponding light is known as linearly polarized light.
It is due to scattering of light by molecules of earth’s atmosphere.
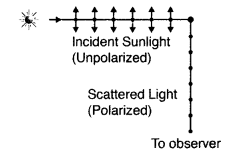
Under the influence of the electric field of the incident (unpolarized) wave, the electrons in the molecules acquire components of motion in both these directions. Charges, accelerating parallel to the double arrows, do not radiate energy towards the observer since their acceleration has no transverse component.
The radiation scattered by the molecules is therefore represented by dots, i.e., it is polarized perpendicular to plane of figure.
Question 40.
State Brewster’s law. The value of Brewster angle for a transparent medium is different for light of different colours. Give reason. (Delhi 2016)
Answer:
(i) Brewster’s law : When unpolarised light is incident on the surface separating two media, the reflected light gets (completely) polarized only when the reflected light and refracted light become perpendicular to each other.
The refractive index of denser medium, with respect to rarer medium, is given by
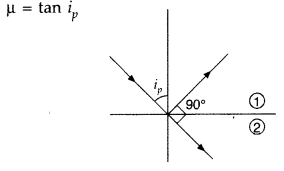
(ii) Since refractive index (µ) of a transparent medium is different for different colours, hence Brewster angle also is different for different colours.
Question 41.
Draw the intensity pattern for single slit diffraction and double slit interference. Hence, state two differences between interference and diffraction patterns. (All India 2017)
Answer:
(i) Intensity distribution in the diffraction due to single slit
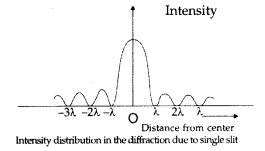
(ii) Intensity pattern for double slit interference.
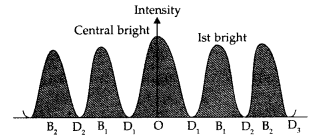
(iii) Difference between Interference and Difference Patterns:
Interference pattern and Diffraction pattern :
The diagram, given here, shows several fringes, due to double slit interference, ‘contained’ in a broad diffraction peak. When the separation between the slits is large compared to their width, the diffraction pattern becomes very flat and we observe the two slit interference pattern.
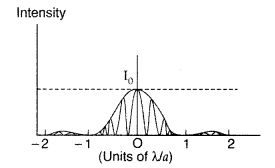
Basic features of distinction between interference and diffraction patterns :
(i) The interference pattern has a number of equally spaced bright and dark bands while diffraction pattern has a central bright maximum which is twice as wide as the other maxima.
(ii) Interference pattern is the superimposition of two waves slits originating from two narrow slits. The diffraction pattern is a superposition of a continuous family of waves originating from each point on a single slit.
(iii) For a single slit of width ‘a’ the first null of diffraction pattern occurs at an angle of \(\frac{\lambda}{a}\). At the same angle of \(\frac{\lambda}{a}\), we get a maxima for two narrow slits separated by a distance ‘a’.
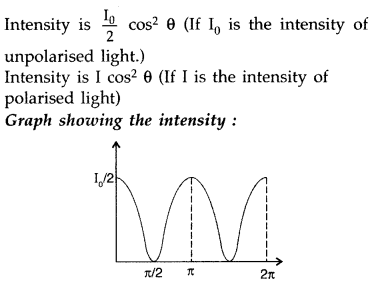
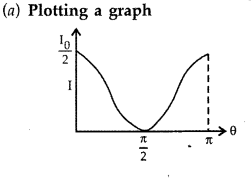
Question 42.
Unpolarised light is passed through a polaroid P
1
When this polarised beam passes through another polaroid P
2
and if the pass axis of P
2
makes angle 6 with the pass axis of P
1
, then write the expression for the polarised beam passing through P
2
. Draw a plot showing the variation of intensity when θ varies from 0 to 2π. (All India 2017)
Answer:
Wave Optics Class 12 Important Questions Short Answer Type SA-II
Question 43.
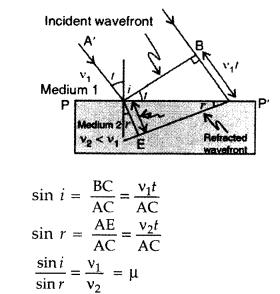
How is a wavefront defined? Using Huygen’s construction draw a figure showing the propagation of a plane wave refracting at a plane surface separating two media. Hence verify Snell’s law of refraction. (Delhi 2008)
Answer:
(i) Wavefront : Wavefront is defined as the continuous locus of all such particles of the medium which are vibrating in the same phase at any instant.
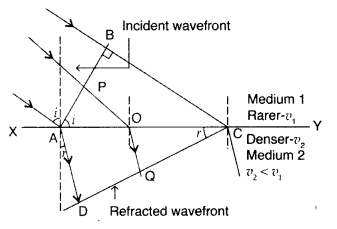
(ii) We take a plane wavefront AB incident at a plane surface XY. We use secondary wavelets starting at different times. We get refracted wavefront only when the time taken by light to travel along different rays from one wavefront to another is same. We take any arbitrary ray starting from point ‘P’ on incident wavefront to refracted wavefront at point ‘O’. Let total time be ‘t’.
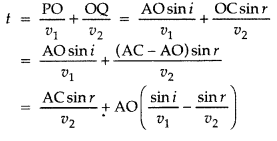
As time should be independent of the ray to be considered
The coefficient of AO in the above equation should be zero
![]()
Where ’µ
2
is called refractive index of medium 2 w.r.t. medium 1. This is Snell’s law of refraction.
Question 44.
How is a wavefront defined? Using Huygen’s construction draw a figure showing the propagation of a plane wave reflecting at the interface of the two media. Shpw that the angle of incidence is equal to the angle of reflection. (Delhi 2008)
Answer:
Wavefront : Wavefront is defined as the continuous locus of all such particles of the medium which are vibrating in the same phase at any instant.
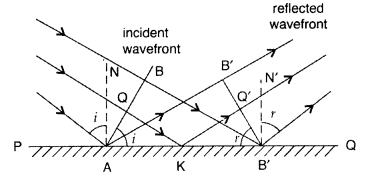
We take any point Q on the incident wavefront. When disturbance from point B on the incident wavefront reaches point B’, the disturbance from point Q reaches Q’ via point K on the reflecting surface. Since B’A’ represents the reflected wavefront, time by light to travel from any point on incident wavefront to the corresponding point on the reflected wavefront should always be same. Let total time be ‘t’
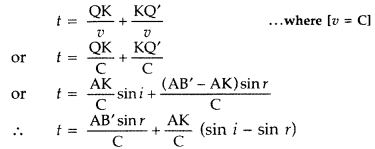
As time of the ray to be considered should be independent, the coefficient of AK in the above equation should be zero.
That is, sin i = sin r or i = r
Hence, angle of incidence is equal to angle of reflection.
Question 45.
Distinguish between unpolarised and plane polarised light. An unpolarised light is incident on the boundry between two transparent media. State the condition when the reflected wave is totally plane polarised. Find out the expression for the angle of incidence in this case. (All India 2008)
Answer:
(a) Unpolarised light: A beam of light in which electrical vector oscillates in all possible planes, in a direction normal to the direction of propagation of wave.
(b) Polarised light : A beam of light in which electrical vector oscillates in a direction normal to the direction of propagation of wave on a single plane only.
From Snell’s law.
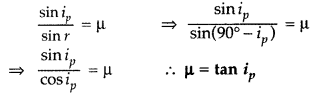
Question 46.
In a single slit diffraction experiment, when a tiny circular obstacle is placed in the path of light from a distance source, a bright spot is seen at the centre of the shadow of the obstacle. Explain why?
State two points of difference between the interference pattern obtained in Young’s double slit experiment and the diffraction pattern due to a single slit. (Delhi 2009)
Answer:
Wave diffracted from the edge of any circular obstacle undergoes constructive interference to form a bright spot at the centre of shadow.
| Young’s double slit experiment | Single slit experiment | |
| 1. |
Light originating
from two coherent sources. |
Light originating
from single source. |
| 2. | Fringes are of equal width. | Fringe width decreases with order. |
| 3. | Intensity of all the bright fringes is the brightness is the same. | Intensity falls with increasing order. The brigtness of successive bright fringes goes on decreasing. |
Question 47.
In Young’s double slit experiment, monochromatic light of wavelength 630 nm illuminates the pair of slits and produces an interference pattern in which two consecutive bright fringes are separated by 8.1 mm. Another source of monochromatic light produces the interference pattern in which the two consecutive bright fringes are separated by 7.2 mm. Find the wavelength of light from the second source. What is the effect on the interference fringes if the monochromatic source is replaced by a source of white light? (All India)
Answer:
Position of the n
th
bright fringe is given by \(\frac{n \lambda \mathrm{D}}{d}\) from the central bright,
So the separation between two consecutive bright
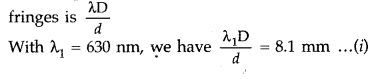
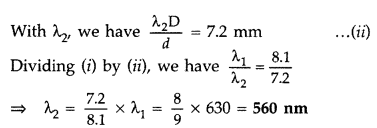
When the monochromatic light is replaced by a white light:
- the central bright remains white and
- all the other colours will form individual maximas with the least wavelength violet forming its bright close to the central bright.
Question 48.
(a) In a single slit diffraction experiment, a slit of width ‘d’ is illuminated by red light of wavelength 650 nm. For what value of ‘d’ will
(i) the first minimum fall at an angle of diffraction of 30°, and
(ii) the first maximum fall at an angle of diffraction of 30°?
(b) Why does the intensity of the secondary maximum become less as compared to the central maximum? (All India 2009)
Answer:

(b) As the order increases only 1/n
th
(where n is an odd number) of the slit, will contribute in producing brightness at a point in diffraction. So the higher order maxima are not so bright as the central.
Question 49.
In Young’s double slit experiment, mono-chromatic light of wavelength 600 nm illuminates the pair of slits and produces an interference pattern in which two consecutive bright fringes are separated by 10 mm. Another source of monochromatic light produces the interference pattern in which the two consecutive bright fringes are separated by 8 mm. Find the wavelength of light from the second source. What is the effect on the interference fringes if the monochromatic source is replaced by a source of white light? (All India 2009)
Answer:
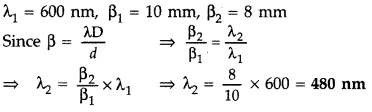
Effect: When the monochromatic light is replaced by a white light:
(i) the central bright remains white and
(ii) all the other colours will form individual maximas with the least wavelength violet forming its bright close to the central bright.
Question 50.
What is an unpolarized light? Explain with the help of suitable ray diagram how an unpolarized light can be polarized by reflection from a transparent medium. Write the expression for Brewster angle in terms of the refractive index of denser medium. (Delhi 2009)
Answer:
Unpolarized light: A light which has vibrations in all directions in a plane perpendicular to the direction of propagation is said to be unpolarized light.
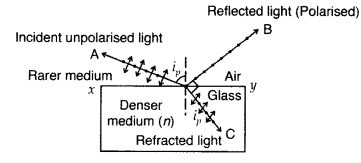
When unpolarised light is incident on the boundary of two transparent media, the reflected light is polarised with electric vector perpendicular to the plane of incidence when the refracted and reflected rays make a right angle with each other.
Relation between Brewster angle i and refractive index (µ) is :
![]()
Question 51.
In Young’s double slit experiment, the two slits 0. 15 mm apart are illuminated by monochromatic light of wavelength 450 nm. The screen is 1.0 m away from the slits.
(a) Find the distance of the second
(i) bright fringe,
(ii) dark fringe from the central maximum.
(b) How will the fringe pattern change if the screen is moved away from the slits? (All India 2009)
Answer:

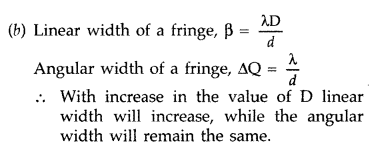
Question 52.
(a) How does an unpolarised light get polarised when passed through a polaroid?
(b) Two polaroids are set in crossed positions. A third polaroid is placed between the two making an angle 0 with the pass axis of the first polaroid. Write the expression for the intensity of light transmitted from the second polaroid. In what orientations will the transmitted intensity by
(i) minimum and
(ii) maximum? (All India 2009)
Answer:
(a) In a polaroid a long chain of molecules is aligned in a particular direction. The electric vectors (of light waves) along the direction of . aligned molecules gets absorbed.
An unpolarised light wave incident on such a polaroid gets linearly polarised with the electric vector oscillating along a direction perpendicular to the aligned molecules. This direction is called pass-axis of the polaroid.
(b) Not in syllabus.
Question 53.
In Young’s double slit experiment, the two slits 0.12 mm apart are illuminated by monochromatic light of wavelength 420 nm. The screeen is 1.0 m away from the slits.
(a) Find the distance of the second
(i) bright fringe,
(ii) dark fringe from the central maximum.
(b) How will the fringe pattern change if the screen is moved away from the slits? (All India 2009)
Answer:

![]()
∴ With increase in the value of D linear width will increase, while the angular width will remain the same.
Question 54.
Describe Young’s double slit experiment to produce interference pattern due to a monochromatic source of light. Deduce the expression for the fringe width. (Delhi 2011)
Answer:
Consider two coherent sources S
1
and S
2
separated by a distance d. Let D be the distance between the screen and the plane of slits S
1
and S
2
.
Light waves emitted from S
1
and S
2
reach point O on the screen after travelling equal distances. So path difference and hence phase difference between these waves is zero. Therefore, they meet at O in phase and hence constructive interference
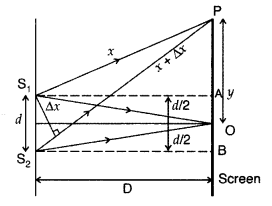
takes place at O. Thus O is the position of the central bright fringe.
Let the waves emitted by S
1
and S
2
meet at point P and the screen at a distance y from the central bright fringe.
The path difference between these waves at P is given by

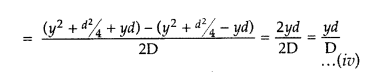
For constructive interference/maxima:
If path difference is an integral multiple of λ, then bright fringe will be formed at P
![]()
…where [m = 1, 2, 3 …
which is the position of mth bright fringe from the central bright fringe.
Fringe width (β) : The distance between any two successive bright fringes (or successive fringes) is called fringe width.
![]()
Destructive interferencelMinima: If path difference is odd multiple of \(\lambda / 2\), then dark fringe is formed at P
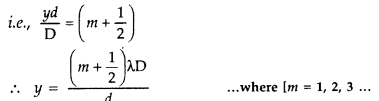
Which is position of m
th
dark fringe from the central bright fringe.
β(fringe width) = y
1
– y
0
![]()
Question 55.
Use Huygen’s principle to verify the laws of refraction. (Delhi 2011)
Answer:
(i) Wavefront : Wavefront is defined as the continuous locus of all such particles of the medium which are vibrating in the same phase at any instant.

(ii) We take a plane wavefront AB incident at a plane surface XY. We use secondary wavelets starting at different times. We get refracted wavefront only when the time taken by light to travel along different rays from one wavefront to another is same. We take any arbitrary ray starting from point ‘P’ on incident wavefront to refracted wavefront at point ‘O’. Let total time be ‘t’.
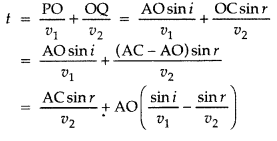
As time should be independent of the ray to be considered
The coefficient of AO in the above equation should be zero
![]()
Where ’µ
2
is called refractive index of medium 2 w.r.t. medium 1. This is Snell’s law of refraction.
Question 56.
(a) Describe briefly, with the help of suitable diagram, how the transverse nature of light can be demonstrated by the phenomenon of polarization.
(b) When unpolarized light passes from air to a transparent medium, under what condition does the reflected light get polarized? (Delhi 2011)
Answer:
(a) Light from a source S is allowed to fall normally on the flat surface of a thin plate of a tourmaline crystal, cut parallel to its axis. Only a part of this light is transmitted through A. If now the plate A is rotated, the character of transmitted light remains unchanged. Now another similar plate B is placed at some distance from A such that the axis of B is parallel to that of A. If the light transmitted through A is passed through B, the light is almost completely transmitted through B and no change is observed in the light coming out of B.
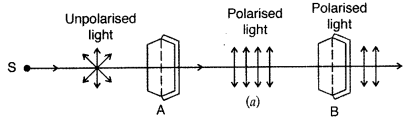
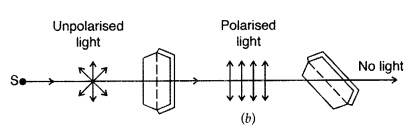
If now the crystal A is kept fixed and B is gradually rotated in its own plane, the intensity of light emerging out of B decreases and becomes zero when the axis of B is perpendicular to that of A. If B is further rotated, the intensity begins to increase and becomes maximum when the axes of A and B are again parallel.
Thus, we see that the intensity of light transmitted through B is maximum when axes of A and B are parallel and minimum when they are at right angles.
From this experiment, it is obvious that light waves are transverse and not longitudinal; because, if they were longitudinal, the rotation of crystal B would not produce any change in the intensity of light.
(b) After falling on a transparent medium, unpolarised light will get polarised after reflection only if refracted and reflected rays make a right angle to each other.
Question 57.
(a) Why are coherent sources necessary to produce a sustained interference pattern?
(b) In Young’s double slit experiment using monochromatic light of wavelength A, the intensity of light at a point on the screen where path difference is A, is K units. Find out the intensity of light at a point where path difference is λ/3. (Delhi 2011)
Answer:
(a) Need of coherent sources for the production of interference pattern. When two monochromatic ‘ waves of intensity I
1
I
2
and phase difference ϕ meet at a point, the resultant intensity is given
![]()
The last term \(2 \sqrt{I_{1} I_{2}}\) cos ϕ is called interference term.
There are two possibilities :
(i) If cos ϕ remains constant with time, the total intensity at any point will be constant. The intensity will be maximum \(\left(\sqrt{I_{1}}+\sqrt{I_{2}}\right)^{2}\) at points when cos ϕ is +1 and minimum \(\left(\sqrt{I_{1}}-\sqrt{I_{2}}\right)^{2}\) at points
where cos ϕ = -1. The sources in this case are coherent.
(ii) If cos ϕ varies continuously with time assuming both positive and negative values, then the average value of cos § will be zero over time interval of measurement. Then interference term averages to zero. There will be same intensity, I = I
1
+ I
2
at every point i.e. there will be general illumination on the observation screen. The two sources in two cases are incoherent.
Hence to observe interference, we need to have two sources with same frequency and with a constant phase difference. Such a pair of sources is called coherent source.
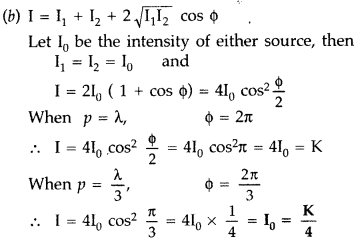
Question 58.
Use Huygens’s principle to explain the formation of diffraction pattern due to a single slit
illuminated by a monochromatic source of light. When the width of the slit is made double the
original width, how would this affect the size and intensity of the central diffraction band?
(Delhi 2011)
Answer:
(a) According to Huygen’s principle “The net effect at any point due to a number of wavelets is equal to sum total of contribution of all wavelets with proper phase difference.”
The point O is maxima because contribution from each half of the slit S
1
S
2
is in phase, i.e., the path difference is zero.
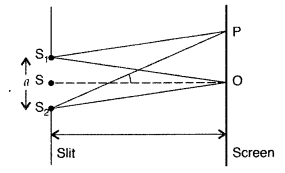
At point P
(i) If S
2
P – S
1
P = nλ ⇒ the point P would be minima.
(ii) If S
2
P – S
1
P = (2n + 1)\(\frac{\lambda}{2} \Rightarrow\) the point would be maxima but with decreasing intensity.

When widths of slits are doubled, contrast between maxima and minima decreases due to the overlapping of interference patterns formed by various narrow pairs of the two slits.
∴ Size of central maxima will be reduced to half and intensity of central maxima will be four times.
Question 59.
(a) Why are coherent sources necessary to produce a sustained interference pattern?
(b) In Young’s double slit experiment using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3. (Delhi 2011)
Answer:
(a) Coherent sources are needed to ensure that the positions of maxima and minima do not change with time. These have a constant phase difference and, therefore produce sustained interference pattern.
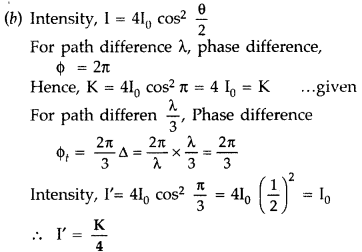
Question 60.
Explain briefly, giving a suitable diagram, how an unpolarised light incident on the interface separating two transparent media gets polarised on reflection. Deduce the necessary condition for it. (Comptt. Delhi 2011)
Answer:
Unpolarized light: A light which has vibrations in all directions in a plane perpendicular to the direction of propagation is said to be unpolarized light.

When unpolarised light is incident on the boundary of two transparent media, the reflected light is polarised with electric vector perpendicular to the plane of incidence when the refracted and reflected rays make a right angle with each other.
Relation between Brewster angle i and refractive index (µ) is :
![]()
Question 61.
(a) In what way is diffraction from each slit related to the interference pattern in a double slit experiment?
(b) Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place at a single slit of aperture 2 × 10
-4
m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases. (Delhi 2011)
Answer:
(a) When there are only a few sources, say two interfering sources, then the result is usually called interference, but if there is a large number of them, it seems that the word diffraction is more often used. In the double slit experiment, we must note that the pattern on the screen is actually a superposition of single slit diffraction from each slit and double slit interference pattern. As a result, there appears a broader diffraction peak in which there occur several fringes of smaller widths due to double slit interference.

Question 62.
(a) Write two characteristic features distinguishing the diffraction pattern from the interference fringes obtained in Young’s double slit experiment.
(b) Two wavelengths of sodium light 590 nm and 596 nm are used, in turn, to study the diffraction taking place due to a single slit of aperture 1 × 10
-4
m. The distance between the slit and the screen is 1.8 m. Calculate the separation between the positions of the first maxima of the diffraction pattern obtained in the two cases. (Delhi 2011)
Answer:
| Diffraction | Interference |
| 1. Width of principal maxima is twice the width of other fringes. | 1. Width of all fringes are the same. |
| 2. Intensity goes on decreasing as order of the diffraction bands increases. | 2. All fringes are of same intensity. |

Question 63.
(a) What is linearly polarized light ? Describe briefly using a diagram how sunlight is polarised.
(b) Unpolarised light is incident on a polaroid. How would the intensity of transmitted light change when the polaroid is rotated? (All India 2011)
Answer:
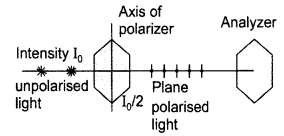
(a) Linearly polarised light : Linearly or plane polarised light is that light in which vibrations of electric field vector are taking place only in one particular plane perpendicular to the direction of propagation of light wave. Sun-light is unpolarised light having electric field vector oscillating in all planes, when it passes through a polariser which can be a nicol prism or tourmaline crystal, only those vibrations of light pass through crystal which are parallel to axis of polarizer and hence we get a plane polarised light having vibrations in one plane. Plane polarized light can be observed by using analyzer.
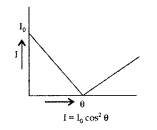
(b) When the polaroid is rotated, the intensity of the transmitted light changes. When the angle of rotation is 45°, the intensity become I
0
/2. When the polaroid is further rotated and at an angle of 90°, the intensity is minimum. Thus the intensity of polarised light changes with the angle of rotation of polaroid. It is shown graphically.
Question 64.
In a modified set-up of Young’s double slit experiment, it is given that SS
2
– SS
1
= λ/4, i.e. the source ‘S’ is not equidistant from the slits S
1
and S
2
.
(a) Obtain the conditions for constructive and destructive interference at any point P on the screen in terms of the path difference δ = S
2
P-S
1
P.
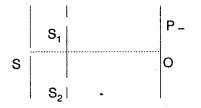
(b) Does the observed central bright fringe lie above or below ‘O’? Give reason to support your answerP
3
(Comptt. All India 2011)
Answer:
(a) Conditions for interferance

Question 65.
(a) Using the phenomenon of polarisation, show how transverse nature of light can be demonstrated?
(b) Two polaroids P
1
and P
2
are placed with their pass axes perpendicular to each other. Unpolarised light of intensity I
0
is incident on P
1
. A third polaroid P
3
is kept in between P
1
and P
2
such that its pass axis makes an angle of 30° with that of P
1
. Determine the intensity of light transmitted through P
1
, P
2
and P
3
. (All India 2011)
Answer:
(a) Light from a source S is allowed to fall normally on the flat surface of a thin plate of a tourmaline crystal, cut parallel to its axis. Only a part of this light is transmitted through A. If now the plate A is rotated, the character of transmitted light remains unchanged. Now another similar plate B is placed at some distance from A such that the axis of B is parallel to that of A. If the light transmitted through A is passed through B, the light is almost completely transmitted through B and no change is observed in the light coming out of B.


If now the crystal A is kept fixed and B is gradually rotated in its own plane, the intensity of light emerging out of B decreases and becomes zero when the axis of B is perpendicular to that of A. If B is further rotated, the intensity begins to increase and becomes maximum when the axes of A and B are again parallel.
Thus, we see that the intensity of light transmitted through B is maximum when axes of A and B are parallel and minimum when they are at right angles.
From this experiment, it is obvious that light waves are transverse and not longitudinal; because, if they were longitudinal, the rotation of crystal B would not produce any change in the intensity of light.
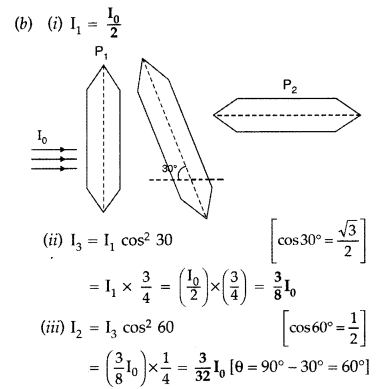
Question 66.
(a) Show, with the help of a diagram, how unpolarised sunlight gets polarised due to scattering.
(b) Two polaroids P
1
and P
2
are placed with their pass axes perpendicular to each other.
Unpolarised light of intensity I
0
is incident on P
1
. A third polaroid P
3
is kept in between P
1
and P
2
such that its pass axis makes an angle of 45° with that of P
1
. Determine the intensity of light transmitted through P
1
, P
2
and P
3
. (All India 2011)
Answer:
(a) Polarisation by scattering. When a beam of white light is passed through a medium, then the beam gets scattered. When the scattered light is seen in a direction perpendicular to the direction of incidence, it is found to be plane polarised. This phenomenon is called polarisation by scattering
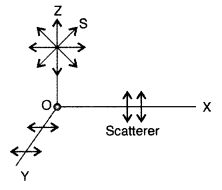
A beam of unpolarised light is incident along Z-axis on a particle. When it is taken along X-axis or Y-axis, then only the vibrations which are parallel to Y-axis or
X-axis, are seen. Hence, light scattered in a direction perpendicular to the incident light is always plane polarised.
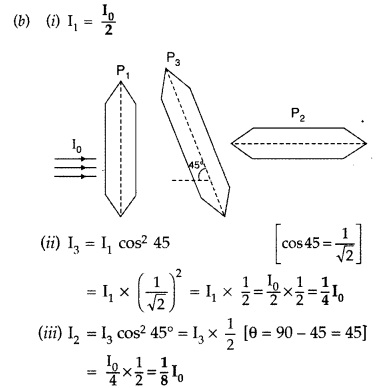
Question 67.
(a) Show, giving a suitable diagram, how unpolarised light can be polarised by reflection.
(b) Two polaroids P
1
and P
2
are placed with their pass axes perpendicular to each other.
Unpolarised light of intensity I
0
is incident on P
1
. A third polaroid P
3
is kept in between P
1
and P
2
such that its pass axis makes an angle of 60° with that of P
1
. Determine the intensity of light transmitted through P
1
, P
2
and P
3
. (All India 2011)
Answer:
(a) Polarisation of light by reflection. The simplest method to produce plane polarised light is by reflection.
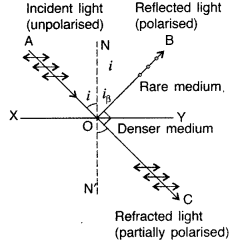
When unpolarised light is reflected from a surface, the reflected light may be completely polarised, partially polarised or unpolarised depending on the incident angle.
The angle of incidence at which the reflected light is completely polarised, is called polarising angle. It is represented by i
β
.
The value of i
β
depends on the wavelength of light used. Therefore, complete polarisation is possible only for monochromatic light. The reflected light along OB is completely plane polarised. The light refracted along OC is unpolarised.
Hence, the reflected light is completely plane polarised in the plane of incidence.
Question 68.
A parallel beam of monochromatic light falls normally on a narrow slit of width ‘a’ to produce a diffraction pattern on the screen placed parallel to the plane of the slit. Use Huygens’ principle to explain that
(i) the central bright maxima is twice as wide as the other maxima.
(ii) the intensity falls as we move to successive maxima away from the centre on either side.
(Comptt. Delhi 2011)
Answer:
(i) In diffraction pattern, intensity will be minimum at an angle θ = nλ/a
∴ There will be a first minimum at an angle
θ = λ/a, on either side of central maximum
∴ Width of central maxima = 2λ/a
∴ The central bright maxima is twice as wide as the other maxima.
(ii) The intensity of maxima decreases as the order (n) or diffraction maxima increases. This is because, on dividing the slit into odd number of parts, the contributions of the corresponding (outermost) pairs cancel each other, leaving behind the contribution of only the innermost segment.
For example, for first maximum, dividing slit into three parts out of these three parts of the slit, the contributions from first two parts cancel each other; only 1/3 rd portion of the slit contributes to the maxima of intensity. Similarly for second maxima, dividing slit into five parts, contribution of first four parts will be zero (as they cancel each other). The remaining 1/5 th portion only will contribute for maxima and so on.
Question 69.
(a) Unpolarised light of intensity I
0
passes through two polaroids P
0
and P
2
such that pass axis of P
2
makes an angle θ with the pass axis of P
1
Plot a graph showing the variation of intensity of light transmitted through P
2
as the angle θ varies from zero to 180°.
(b) A third polaroid P
3
is placed between P
1
and P
2
with pass axis of P
3
making an angle β with that of P
1
. If I
1
I
2
and I
3
represent the intensities of light transmitted by P
1
, P
2
and P
3
, determine the values of angle θ and β for which I
1
= I
2
= I
3
. (Comptt. All India 2011)
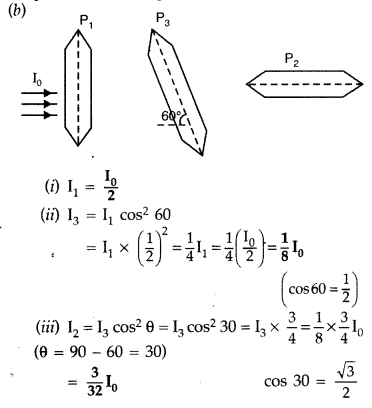
Answer:
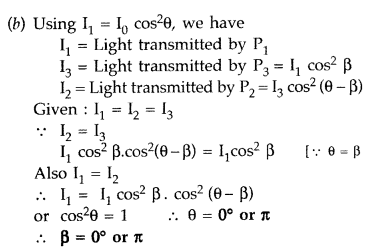
Question 70.
(a) Two monochromatic waves emanating from two coherent sources have the displacements represented by
y
1
= a cos ωt and y
2
= a cos (ωt + ϕ ), where ϕ is the phase difference between the two displacements. Show that the resultant intensity at a point due to their superposition is given by I = 4I
0
cos
2
ϕ/2, where I
0
= a
2
.
(b) Hence obtain the conditions for constructive and destructive interference. (Comptt. All India 2011)
Answer:
(a) (i) Two independent monochromatic
sources of light cannot produce a sustained interference pattern. The phase difference between these two sources will continuously vary; and the positions of maxima and minima will change with time.
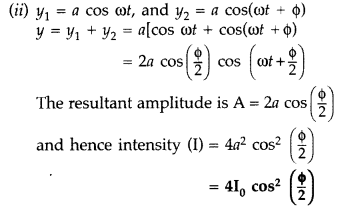
(b) (i) For constructive interference :
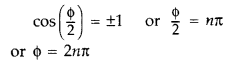
(ii) For destructive interference:
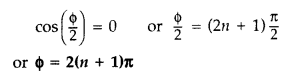
Question 71.
Answer the following questions:
(i) In a double slit experiment using light of wavelength 600 nm, the angular width of the fringe formed on a distant screen is 0.1°. Find the spacing between the two slits.
(ii) Light of wavelength 5000 A propagating in air gets partly reflected from the surface of water. How will the wavelengths and frequencies of the reflected and refracted light be affected? (Delhi 2015)
Answer:

(ii) For reflected light : Wavelength remains same and frequency remains the same.
For refracted light : Wavelength decreases, but frequency remains the same.
Question 72.
State clearly how an unpolarised light gets linearly polarised when passed through a Polaroid.
(i) Unpolarised light of intensity I
0
is incident on a polaroid P
1
which is kept near another Polaroid P
2
whose pass axis is parallel to that of P
1
. How will the intensities of light, I
1
and I
2
, transmitted by the polaroids P
1
and P
2
respectively, change on rotating Px without disturbing P
2
?
(ii) Write the relation between the intensities I
1
and I
2
. (All India 2015)
Answer:
When unpolarised light is passed through a polaroid, the light wave will get linearly polarised with the electric vector oscillating along a direction perpendicular to the aligned molecules.
![]()
I
1
remains unchanged on rotating Pj; while, according to Malus’ law,
![]()
when P
1
is rotated.
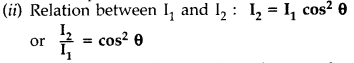
Question 73.
Use Huygens’ principle to show how a plane wavefront propagates from a denser to rarer medium. Hence verify Snell’s law of refraction. (All India 2015)
Answer:
Huygens’ geometrical construction for a plane wave propagation. Let AB be a section of primary wavefront at any instant t. Take points 1, 2, 3, 4, … on the wavefront AB. Taking each point as centre, draw spheres of radius r = ct, where c is the velocity of light in the medium.
Draw a surface A
1
B
1
touching tangentially at the secondary wavelets in the forward direction. The surface A
1
B
1
is the secondary wavefront after time t.
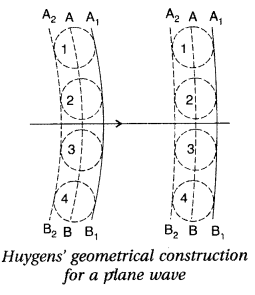
A surface A
2
B
2
touching tangentially all the secondary wavelets in the backward direction can be drawn to give a backward secondary wavefront.
Laws of refraction using Huygen’s principle. Let XY be the refracting surface separating two mediums 1
st
and 2
nd
. Let c
1
and c
2
be the velocities of light in these mediums.
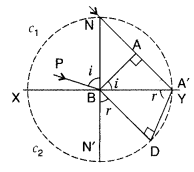
Let AB be a plane wavefront moving through the surface XY meeting at the point B.
The time taken ‘t’ of A to reach at A’B then

To obtain new front, draw a circle with point B as centre and BD as radius in 2nd medium. Draw a tangent A’D from point A’. Then A’D represents the refracted wavefront.
Since PB be incident ray and BD be refracted ray

This constant V is called the refractive index of material which proves Snell’s law of refraction.
Question 74.
Explain by drawing a suitable diagram that the interference pattern in a double slit is actually a superposition of single slit diffraction from each slit.
Write two basic features which distinguish the interference pattern from those seen in a coherently illuminated single slit. (Comptt. Delhi 2015)
Answer:
Interference pattern and Diffraction pattern :
The diagram, given here, shows several fringes, due to double slit interference, ‘contained’ in a broad diffraction peak. When the separation between the slits is large compared to their width, the diffraction pattern becomes very flat and we observe the two slit interference pattern.

Basic features of distinction between interference and diffraction patterns :
(i) The interference pattern has a number of equally spaced bright and dark bands while diffraction pattern has a central bright maximum which is twice as wide as the other maxima.
(ii) Interference pattern is the superimposition of two waves slits originating from two narrow slits. The diffraction pattern is a superposition of a continuous family of waves originating from each point on a single slit.
(iii) For a single slit of width ‘a’ the first null of diffraction pattern occurs at an angle of \(\frac{\lambda}{a}\). At the same angle of \(\frac{\lambda}{a}\), we get a maxima for two narrow slits separated by a distance ‘a’.
Question 75.
(a) The ratio of the widths of two slits in Young’s double slit experiment is 4 : 1. Evaluate the ratio of intensities at maxima and minima in the interference pattern.
(b) Does the appearance of bright and dark fringes in the interference pattern violate, in any way, conservation of energy? (Comptt. All India 2015)
Answer:

(b) The appearance of bright and dark fringes in the interference pattern does not violate the principle of conservation of energy, because the light energy is distributed. If it reduces in one region, producing a dark fringe, it increases in another region, producing a bright fringe. There is no gain or loss of energy.
Question 76.
(a) Good quality sun-glasses made of polaroids are preferred over ordinary coloured glasses. Justify your answer.
(b) Two polaroids P
1
and P
2
are placed in crossed positions. A third polaroid P
3
is kept between P
3
and P
2
such that pass axis of P
3
is parallel to that of P
1
. How would the intensity of light (I
2
) transmitted through P
2
vary as P
3
is rotated? Draw a plot of intensity I
2
‘ vs the angle ‘θ’ between pass axes of P
1
and P
3
. (Comptt. All India 2015)
Answer:
(a) Such good quality sun-glasses made of polaroids are preferred ’ over ordinary coloured glasses because they protect the eyes from the glare.
(b)
Let the rotating Polaroid sheet make an angle θ with the first polaroid.
∴ angle with the other polaroid will be (90 – θ)

Question 77.
(i) State law of Malus.
(ii) Draw a graph showing the variation of intensity (I) of polarised light transmitted by an analyser with angle (θ) between polariser and analyser.
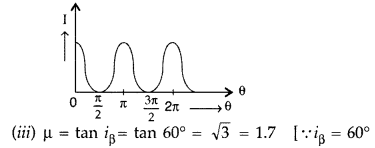
(iii) What is the value of refractive index of a medium of polarising angle 60°?(All India 2015) Answer:
(i) Law of Malus : When the pass axis of a poloroid makes an angle 0 with the plane of polarisation of polorised light of intensity I0 incident on it, then the intensity of the transmitted emergent light is given by
I = I
0
cos
2
θ
(ii) Variation of intensity with θ
Question 78.
Define the term wave front. State Huygen’s principle.
Consider a plane wave front incident on a thin convex lens. Draw a proper diagram to show how the incident wave front traverses through the lens and after refraction focusses on the focal point of the lens, giving the shape of the emergent wave front. (All India 2015)
Answer:
(i) Wave front : It is defined as the locus of all points which oscillate in phase.
(ii) Huygen’s Principle :
1 Each point of the wave front is the source of a secondary disturbance and the wavelets emanating from these points spread out in all directions. These travel with the same velocity as that of the original wave front.
2. The shape and position of the wave front, after time Y, is given by the tangential envelope to the secondary wavelets.
(iii) Refraction of a plane wave-front from a convex lens
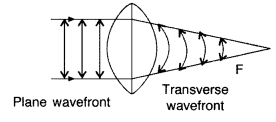
Question 79.
The figure, drawn here, shows the geometry of path differences for diffraction by a single slit of width a.
Give appropriate ‘reasoning’ to explain why the intensity of light is
(i) maximum of the central point C on the screen.
(ii) (nearly) zero for point P on the screen when
![]()
Hence write an expression for the total linear width of the central maxima on a screen kept at a distance D from the plane of the slit. (Comptt. Delhi 2015)
Answer:
(i) At central point C, angle θ is zero, all path differences are zero. Hence, all the parts of the slit contribute in same phase. This gives maximum intensity at point C.
(ii) From the diagram :
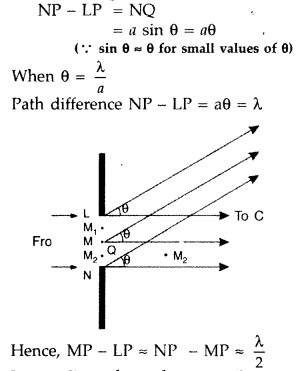
It implies that the contribution from corresponding points in two halves of the slit have a phase difference of π. Therefore, contributions from two halves cancel each other in pairs, resulting in a zero net intensity at point P on the screen.

Question 80.
Two polaroids, P
1
and P
2
, are ‘set-up’ so that their ‘pass-axis’ are ‘crossed’ with respect to each other. A third polaroid, P
3
, is now introduced between these two so that its ‘pass-axis’ makes an angle θ with the ‘pass-axis’ of P
1
.
A beam of unpolarised light, of intensity I, is incident on P
1
If the intensity of light, that gets transmitted through this combination of three polaroids, is I’, find the ratio \(\left(\frac{\mathbf{I}^{\prime}}{\mathbf{I}}\right)\) when θ equals :
(i) 30°,
(ii) 45° (Comptt. Delhi 2015)
Answer:
A beam of unpolarised light of intensity I is incident on P
1
.
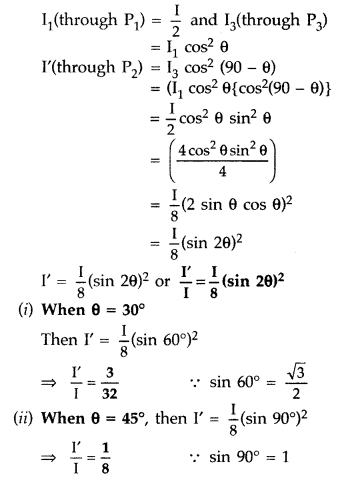
Question 81.
A plane wavefront is incident at an angle of incidence i on a reflecting surface. Draw a diagram showing incident wavefront, reflected wavefront and verify the laws of reflection. (Comptt. Delhi 2015)
Answer:
Diagram of a plane wave front for Reflection :
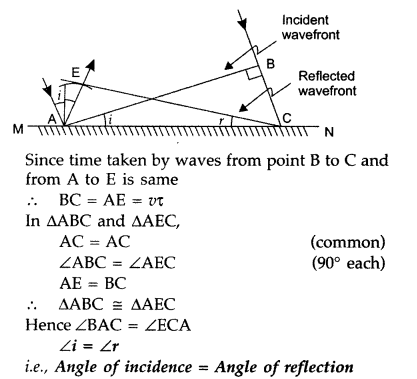
Question 82.
(a) In a Young’s double slit experiment, the two slits are illuminated by two different lamps having same wavelength of light. Explain with reason, whether interference pattern will be observed on the screen or not.
(b) Light waves from two coherent sources arrive at two points on a screen with path differences of 0 and A/2. Find the ratio of intensities at the points. (Comptt. All India 2015)
Answer:
(a) Interference pattern in Young’s double slit experiment will not be observed, because two independent lamps do not constitute ‘coherent sources’.
(b) (i) When path difference is zero, corresponding phase difference will also be zero.
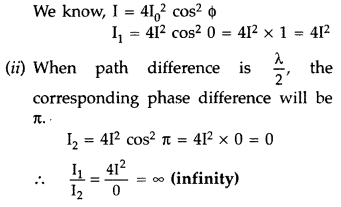
Question 83.
(a) Explain how the intensity of diffraction pattern changes as the order (n) of the diffraction band varies.
(b) Two wavelengths of sodium light 590 nm and 596 nm are used in turn to study the diffraction at a single slit of size 4 mm. The distance between the slit and screen is 2 m. Calculate the separation between the positions of the first maximum of the diffraction pattern obtained in the two cases. (Comptt. All India 2015)
Answer:
(a) Intensity of diffraction pattern drops rapidly with order n, because every higher order
maxima gets intensity only from \(\left(\frac{1}{2 n+1}\right)\) part of the slit. The central maxima gets intensity from the whole slit (n = 0).
1
st
secondary maxima gets its intensity only from 1/3 of slit.
2
nd
secondary maxima gets its intensity only from 1/5 of slit and so on.
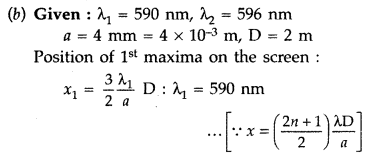
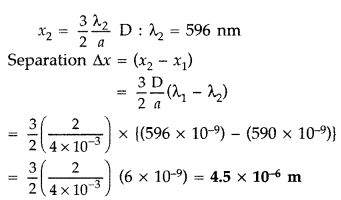
Question 84.
Why are coherent sources necessary to produce interference in Young’s double slit experiment? Light waves from two coherent sources have intensities in the ratio of 4 : 9. Find the ratio of intensities of maxima and minima in the interference pattern. (Comptt. Delhi 2015)
Answer:
If sources are not coherent, the superposition pattern (intensity pattern) is not stable. It keeps on changing with time and hence it is necessary to have coherent sources to observe interference in Young’s double slit experiment.
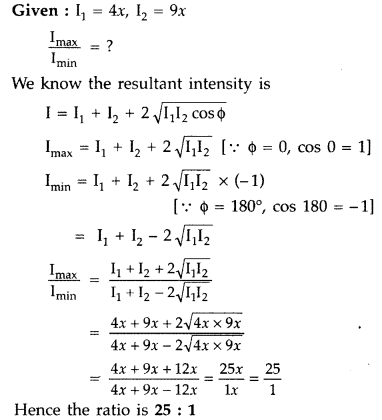
Question 85.
State the two features to distinguish between interference and diffraction phenomena. Two wavelengths of light 600 nm and 610 nm are used in turn, to study the diffraction at a single slit of size 2 mm. The distance between the slits and screen is 2 m. Calculate the separation between the positions of the second order maximum of the diffraction pattern obtained in the two cases. (Comptt. All India 2015)
Answer:
For distinction between interference and diffraction :
Interference pattern and Diffraction pattern :
The diagram, given here, shows several fringes, due to double slit interference, ‘contained’ in a broad diffraction peak. When the separation
between the slits is large compared to their width, the diffraction pattern becomes very flat and we observe the two slit interference pattern.

Basic features of distinction between interference and diffraction patterns :
(i) The interference pattern has a number of equally spaced bright and dark bands while diffraction pattern has a central bright maximum which is twice as wide as the other maxima.
(ii) Interference pattern is the superimposition of two waves slits originating from two narrow slits. The diffraction pattern is a superposition of a continuous family of waves originating from each point on a single slit.
(iii) For a single slit of width ‘a’ the first null of diffraction pattern occurs at an angle of \(\frac{\lambda}{a}\). At the same angle of \(\frac{\lambda}{a}\), we get a maxima for two narrow slits separated by a distance ‘a’.
Given : λ
1
= 600 nm = 600 × 10
-9
m,

Wave Optics Class 12 Important Questions Long Short Answer Type
Question 86.
(a) What is plane polarised light? Two polaroids are placed at 90° to each other and the transmitted intensity is zero. What happens when one more polaroid is placed between these two, bisecting the angle between them? How will the intensity of transmitted light vary on further rotating the third polaroid?
(b) If a light beam shows no intensity variation when transmitted through a polaroid which is rotated, does it mean that the light is unpolarised? Explain briefly. (Delhi 2015)
Answer:
(a) Plane polarised light is the light wave in which optical vector (electric vector) oscillates only in a single plane in a direction perpendicular to the direction of propagation of wave.
Obviously, the axis of P
3
is inclined at 45° to the axis of P
1
and P
2
.
Let the maximum intensity transmitted by polarised,
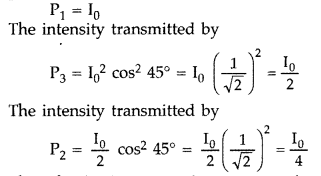
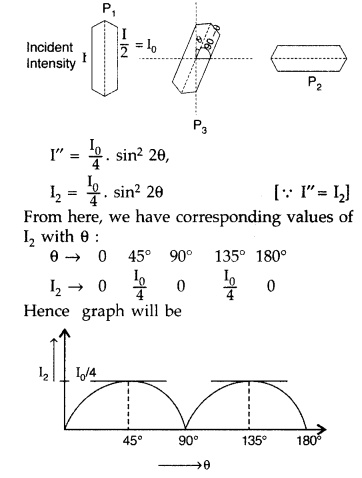
Thus the final intensity becomes one-fourth of the maximum intensity transmitted by the first polariod. On further rotating the third polaroid, the intensity of transmitted light decreases till it becomes zero.
(b) Yes, the light beam is unpolarised. The polaroid cuts down the intensity to half due to polarisation of light. When polaroid is rotated, only the plane of polarisation rotates but the intensity of light does not show any change.
Question 87.
(a) What are coherent sources of light? Two slits in Young’s double slit experiment are illuminated by two different sodium lamps emitting light of the same wavelength. Why is no interference pattern observed?
(b) Obtain the condition for getting dark and bright fringes in Young’s experiment. Hence write the expression for the fringe width.
(c) If s is the size of the source and its distance is a from the plane of the two slits, what should be the criterion for the interference fringes to be seen? (All India 2015)
Answer:
(a) Two sources of light having same frequency and a constant or a zero phase difference are said to be coherent.
Light wave emitted from an ordinary source (like a sodium lamp) undergoes abrupt phase changes in times of the order of 10
-10
seconds. Thus two independent sources of light will not have a fixed phase relationship and would be incoherent.

Question 88.
State Huygens’s principle. Show, with the help of a suitable diagram, how this principle is used to obtain the diffraction pattern by a single slit. Draw a plot of intensity distribution and explain clearly why the secondary maxima become weaker with increasing order (n) of the secondary maxima. (Delhi 2010)
Answer:
Huygen’s principle :
“(i) Each point on a wavefront acts as a fresh source of new disturbance called secondary waves or wavelets;
(ii) The secondary wavelets spread out in all directions with the speed of wave in the given medium;
(iii) The new wavefront at any later time is given by the forward envelope (tangential surface in the forward direction) of the secondary wavelets at that time.
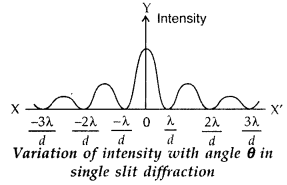
The reason is that the intensity of the central maxima is due to the constructive interference of wavelets from all parts of the slit, the first secondary maxima is due to the contribution of wavelets from one third part of the slit (wavelets from remaining two parts interfere destructively), the second secondary maxima is due to the contribution of wavelets from the one fifth part only (the remaining four parts interfere destructively) and so on. Hence, the intensity’ of secondary maxima decreases with the increase in the order n of the maxima.
Question 89.
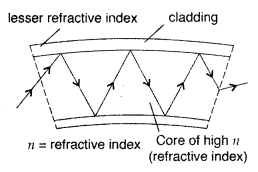
Explain briefly how the phenomenon of total internal reflection is used in fibre optics. (Delhi 2011)
Answer:
Each optical fibre consists of a core and cladding. Refractive index of the material of the core is higher than that of cladding. When a video signal is directed into an optical fibre at a suitable angle, it undergoes internal reflections repeatedly along the length of the optical fibre and comes out of it with almost neglible loss of intensity.
Question 90.
(i) State the importance of coherent sources in the phenomenon of interference.
(ii) In Young’s double slit experiment to produce interference pattern, obtain the conditions for constructive and destructive interference. Hence deduce the expression for the fringe width.
(iii) How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water? (All India 2010)
Answer:
(i) Importance of coherent source : Coherent sources are necessary to produce sustained interference pattern. Otherwise the phase difference between the two interfering waves will change rapidly and the interference pattern will be lost. .
(ii)
(a) For constructive interference : We will have constructive interference resulting in a bright fringe when path difference is equal to nλ.
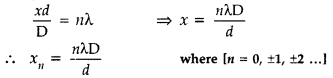
Since the separation between the centres of two consecutive bright fringes is called fringe width. It is denoted by β
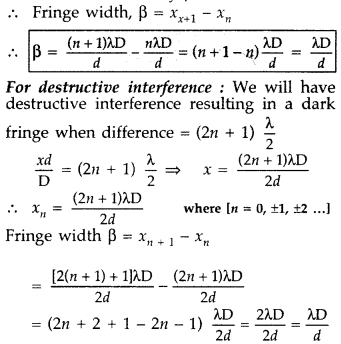
Hence all bright and dark fringes are of equal width.
Observations :
(i) Fringe width is directly proportional to the wavelength of light i.e. p X.
(ii) Fringe width is inversely proportional to the distance between two sources
![]()
(iii) Fringe width is directly proportional to the distance between screen and two sources i.e. \(\beta \propto \frac{1}{d}\).
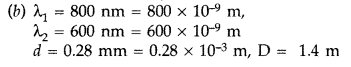
Suppose at any distance x from the central maximum,
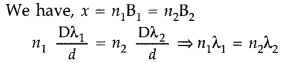
The bright fringes will coincide at the least distance x,
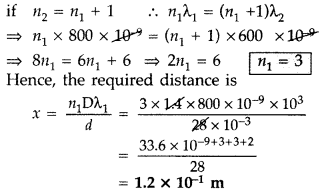
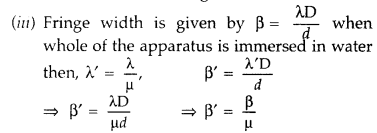
Then fringe width becomes \(\frac{\mathbf{1}}{\mu}\) times the original fringe width i.e., it will decrease in water.
Question 91.
(a) State Huygen’s principle. Using this principle explain how a diffraction pattern is obtained on a screen due to a narrow slit on which a narrow beam coming from a monochromatic source of light is incident normally.
(b) Show that the angular width of the first diffraction fringe is half of that of the central fringe.
(c) If a monochromatic source of light is replaced by white light, what change would you observe in the diffraction pattern? (All India 2011)
Answer:
(a)
Huygen’s principle :
“(i) Each point on a wavefront acts as a fresh source of new disturbance called secondary waves or wavelets;
(ii) The secondary wavelets spread out in all directions with the speed of wave in the given medium;
(iii) The new wavefront at any later time is given by the forward envelope (tangential surface in the forward direction) of the secondary wavelets at that time.

The reason is that the intensity of the central maxima is due to the constructive interference of wavelets from all parts of the slit, the first secondary maxima is due to the contribution of wavelets from one third part of the slit (wavelets from remaining two parts interfere destructively), the second secondary maxima is due to the contribution of wavelets from the one fifth part only (the remaining four parts interfere destructively) and so on. Hence, the intensity’ of secondary maxima decreases with the increase in the order n of the maxima.

(c) If monochromatic source of light is replaced by a source of white light, instead of white fringes we obtain few coloured fringes and then uniform illumination.
Question 92.
(a) In Young’s double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
(b) A beam of light consisting of two wavelenths, 800 nm and 600 nm is used to obtain the interference fringes in a Young’s double slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide. (All India 2011)
Answer:
(a) For constructive interference : We will have constructive interference resulting in a bright fringe when path difference is equal to nλ.
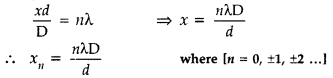
Since the separation between the centres of two consecutive bright fringes is called fringe width. It is denoted by β
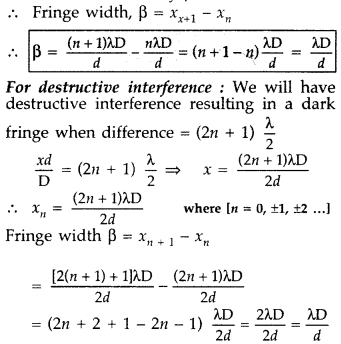
Hence all bright and dark fringes are of equal width.
Observations :
(i) Fringe width is directly proportional to the wavelength of light i.e. p X.
(ii) Fringe width is inversely proportional to the distance between two sources
![]()
(iii) Fringe width is directly proportional to the distance between screen and two sources i.e. \(\beta \propto \frac{1}{d}\).
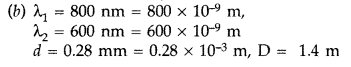
Suppose at any distance x from the central maximum,
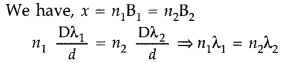
The bright fringes will coincide at the least distance x,
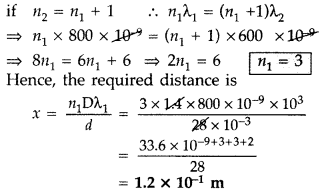
Question 93.
(a) How does an unpolarized light incident on a polaroid get polarized?
Describe briefly, with the help of a necessary diagram, the polarization of light by reflection from a transparent medium.
(b) Two polaroids ‘A’ and ‘B’ are kept in crossed position. How should a third polaroid ‘C’ be placed between them so that the intensity of polarized light transmitted by polaroid B reduces to 1/8* of the intensity of unpolarized ‘ light incident on A? (All India 2010)
Answer:
(a) In a polaroid a long chain of molecules is aligned in a particular direction. The electric vectors (of light waves) along the direction of . aligned molecules gets absorbed.
Diagram of polarization of light by reflection.
Polarisation of light by reflection. The simplest method to produce plane polarised light is by reflection.

When unpolarised light is reflected from a surface, the reflected light may be completely polarised, partially polarised or unpolarised depending on the incident angle.
The angle of incidence at which the reflected light is completely polarised, is called polarising angle. It is represented by i
β
.
The value of i
β
depends on the wavelength of light used. Therefore, complete polarisation is possible only for monochromatic light. The reflected light along OB is completely plane polarised. The light refracted along OC is unpolarised.
Hence, the reflected light is completely plane polarised in the plane of incidence.(b) Let the intensity of unpolarized light = I
0
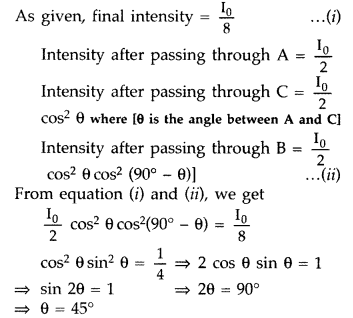
Hence, the angle between polaroid A and C should be 45°.
Question 94.
(a) State Huygen’s principle. Using this principle draw a diagram to show how a plane wave front incident at the interface of the two media gets refracted when it propagates from a rarer to a denser medium. Hence verify Snell’s law of refraction.
(b) When monochromatic light travels from a rarer to a denser medium, explain the following, giving reasons :
(i) Is the frequency of reflected and refracted light same as the frequency of incident light?
(ii) Does the decrease in speed imply a reduction in the energy carried by light wave? (Delhi 2010)
Answer:
(a) Huygen’s principle ; Huygen’s principle is based on two assumptions :
(i) Each point on the primary wavefront is a source of a new disturbance called secondary wavelets which travel in all directions with same velocity as that of original waves.
(ii) A surface tangential to the secondary . wavelets gives the position and shape of new wavefront at any instant. This is called secondary wavefront.
The principle leads to the well known laws of reflection and refraction.
Verification of Snell’s Law, From the figure
(b) (i) Yes, frequency is the property of source. Hence, frequency does not change when light is reflected or refracted.
(ii) No, decrease in speed does not imply reduction in energy carried by light wave.
This is because the frequency does not change and according to the formula E = hv, energy will be independent of speed. Energy carried by a wave depends on the amplitude of the wave, not on the speed of wave propagation.
Question 95.
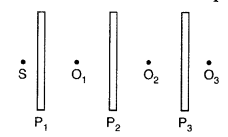
(a) Describe briefly how an unpolarized light gets linearly polarized when it passes through a polaroid.
(b) Three identical polaroid sheets P3, P2 and P3 are oriented so that the pass axis of P
1
, P
2
and P
3
are inclined at angles of 60° and 90° respectively with respect to the pass axis of P
1
. A monochromatic source S of unpolarized light of intensity I
0
is kept in front of the polaroid sheet P
1
as shown in the figure. Determine the intensities of light as observed by the observers O
1
O
2
and O
3
as shown. (Comptt. Delhi 2010)
Answer:
(a) A polaroid consists of long chain molecules aligned in a particular direction. The electric vectors (associated with the propagating light wave) along the direction of the aligned molecules get absorbed. Thus, if an unpolarised light wave is incident on such a polaroid then the light wave will get linearly polarised with the electric vector oscillating along a direction perpendicular to the aligned molecules.
Question 96.
(a) Use Huygen’s geometrical construction to show how a plane wave-front at t = 0 propagates and produces a wave-front at a later time.
(b) Verify, using Huygen’s principle, Snell’s law of refraction of a plane wave propagating from a denser to a rarer medium.
(c) When monochromatic light is incident on a surface separating two media, the reflected and refracted light both have the same frequency. Explain why. (Comptt. Delhi)
Answer:
(a) Huygens’ geometrical construction for a plane wave propagation.
Huygens’ geometrical construction for a plane wave propagation. Let AB be a section of primary wavefront at any instant t. Take points 1, 2, 3, 4, … on the wavefront AB. Taking each point as centre, draw spheres of radius r = ct, where c is the velocity of light in the medium.
Draw a surface A
1
B
1
touching tangentially at the secondary wavelets in the forward direction. The surface A
1
B
1
is the secondary wavefront after time t.

A surface A
2
B
2
touching tangentially all the secondary wavelets in the backward direction can be drawn to give a backward secondary wavefront.
Laws of refraction using Huygen’s principle. Let XY be the refracting surface separating two mediums 1
st
and 2
nd
. Let c
1
and c
2
be the velocities of light in these mediums.

Let AB be a plane wavefront moving through the surface XY meeting at the point B.
The time taken ‘t’ of A to reach at A’B then

To obtain new front, draw a circle with point B as centre and BD as radius in 2nd medium. Draw a tangent A’D from point A’. Then A’D represents the refracted wavefront.
Since PB be incident ray and BD be refracted ray

This constant V is called the refractive index of material which proves Snell’s law of refraction.
(b) Laws of refraction using Huygen’s principle.
Huygens’ geometrical construction for a plane wave propagation. Let AB be a section of primary wavefront at any instant t. Take points 1, 2, 3, 4, … on the wavefront AB. Taking each point as centre, draw spheres of radius r = ct, where c is the velocity of light in the medium.
Draw a surface A
1
B
1
touching tangentially at the secondary wavelets in the forward direction. The surface A
1
B
1
is the secondary wavefront after time t.

A surface A
2
B
2
touching tangentially all the secondary wavelets in the backward direction can be drawn to give a backward secondary wavefront.
Laws of refraction using Huygen’s principle. Let XY be the refracting surface separating two mediums 1
st
and 2
nd
. Let c
1
and c
2
be the velocities of light in these mediums.

Let AB be a plane wavefront moving through the surface XY meeting at the point B.
The time taken ‘t’ of A to reach at A’B then

To obtain new front, draw a circle with point B as centre and BD as radius in 2nd medium. Draw a tangent A’D from point A’. Then A’D represents the refracted wavefront.
Since PB be incident ray and BD be refracted ray

This constant V is called the refractive index of material which proves Snell’s law of refraction.
(c) When monochromatic light is incident on a surface separating two media, the redacted and refracted lights both have the same frequency.
In case of refraction, due to change in medium, only wavelength changes by λ/µ factor.
In case of reflection, both wavelength and frequency remain unchanged.
Question 97.
(a) (i) “Two independent monochromatic sources of light cannot produce a sustained interference pattern”. Give reason.
(ii) Light waves each of amplitude “a” and frequency “ω”, emanating from two coherent light sources superpose at a point. If the displacements due to these waves is given by y
1
= a cos ωt and y
2
= a cos(ωt + ϕ ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young’s double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3. (Delhi 2010)
Answer:
(a) (i) Two independent monochromatic
sources of light cannot produce a sustained interference pattern. The phase difference between these two sources will continuously vary; and the positions of maxima and minima will change with time.
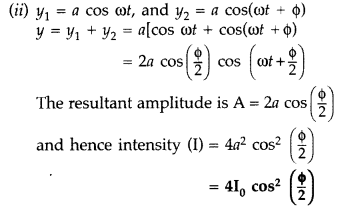
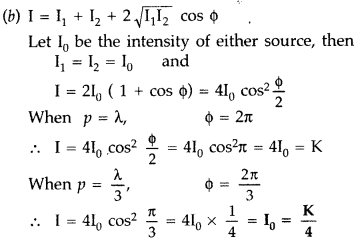
Question 98.
(a) How does one demonstrate, using a suitable diagram, that unpolarised light when passed through a Polaroid gets polarised?
(b) A beam of unpolarised light is incident on a glass-air interface. Show, using a suitable ray diagram, that light reflected from the interface is totally polarised, when μ = tan i
B
, where μ is the refractive index of glass with respect to air and i
B
is the Brewster’s angle. (Delhi 2014)
Answer:
(a) Polarisation of light. Ordinary light is unpolarised light having vibrations distributed in all directions in a plane perpendicular to direction of propagation of light.
Therefore, the phenomenon of restricting the vibrations of light in a particular direction is called polarisation of light. The tourmaline crystal acts as a polariser.
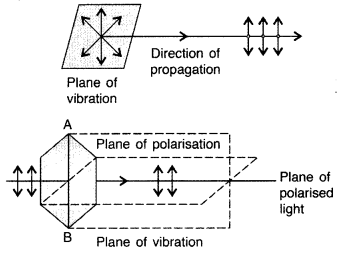
When unpolarised light (ordinary light) is passed through a tourmaline crystal, only those vibrations of light pass through the crystal which are parallel to crystallographic axis AB. All other vibrations are obstructed. The entering light from the crystal is said to be plane polarised light.
(b) When unpolarised light is reflected from a surface, the reflected light may be completely polarised, partially polarised or unpolarised depending on the incident angle.
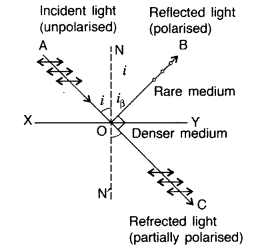
The angle of incidence at which the reflected light is completely polarised, is called polarising angle. It is represented by i
β
.
The value of i
β
depends on the wavelength of light used. Therefore, complete polarisation is possible only for monochromatic light. The reflected light along OB is completely plane polarised. The light refracted along OC is unpolarised.
Hence, the reflected light is completely plane polarised in the plane of incidence. Brewster’s law. It states that “when light is incident at polarising angle, the reflected and refracted rays are perpendicular to each other”. When light is incident at polarising angle, the reflected component along OB and refracted components along OC are mutually perpendicular.
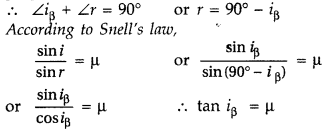
Hence, the tangent of the polarising angle is equal to the refractive index of a medium
Question 99.
(a) In Young’s double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
(b) The ratio of the intensities at minima to the maxima in the Young’s double slit experiment is 9 : 25. Find the ratio of the widths of the two slits. (All India 2014)
Answer:
(a) Young’s double slit experiment. The path difference between two rays coming from holes S
1
and S
2
is (S
2
P – S
1
P). If point P corresponds to a maximum,
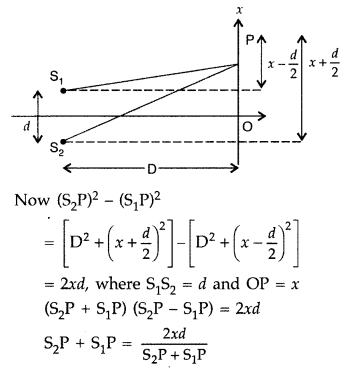
If x, d << D, then negligible error will be introduced if (S
2
P + S
1
P) in the denominator is replaced by 2D.

Thus, bright and dark bands appear on the screen. Such bands are called ‘fringes’.
These dark and bright fringes are equally spaced.

Question 100.
(a) Describe briefly how a diffraction pattern is obtained on a screen due to a single narrow slit illuminated by a monochromatic source of light. Hence obtain the conditions for the angular width of secondary maxima and secondary minima.
(b) Two wavelengths of sodium light of 590 nm and 596 nm are used in turn to study the diffraction taking place at a single slit of aperture 2 × 10
-6
m. The distance between the slit and the screen is 1.5 m. Calculate the separation between the positions of first maxima of the diffraction pattern obtained in the two cases. (All India 2014)
Answer:
(a) Diffraction at a single slit. Suppose a parallel beam of monochromatic light of wavelength X falls normally on a slit AB of width d (of the order of the wavelength of light). The diffraction occurs on passing through the slit. The diffraction pattern is focussed on to the screen by a convex lens. The diffraction pattern consists of a central bright fringe (or band), having alternate dark and bright fringes of decreasing intensity on both sides.
1. Position of central maximum. Let C be the centre of the slit AB. According to Huygen’s principle, “when.light falls on the slit, it becomes a source of secondary wavelets.” All the wavelets originating from slit AB are in same phase. These secondary waves reinforce each other resulting the central maximum intensity at O.
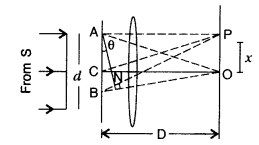
2. Position of secondary maxima and minima. Consider a point P on the screen. All the secondary waves travelling in a direction making angle θ with CO, reach at a point P. The intensity at P depends on the path difference between secondary waves.
∴ Path difference between the secondary waves reaching P from points A and B is, BN = d sin θ
(i) The point P will be the position of n
th
secondary maxima

(ii) The point P will be the position of n
th
secondary minima,
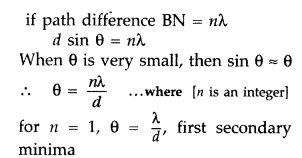
Hence, the diffraction pattern due to single slit consists of a centre bright maximum at O alongwith secondary maxima and minima on either side. Intensity distribution curve. The intensity distribution on the screen.is represented as shown in the figure.
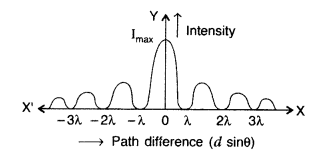
Width of central maximum. If D is the distance between slit and screen and yn is the distance of nth minimum from point O,
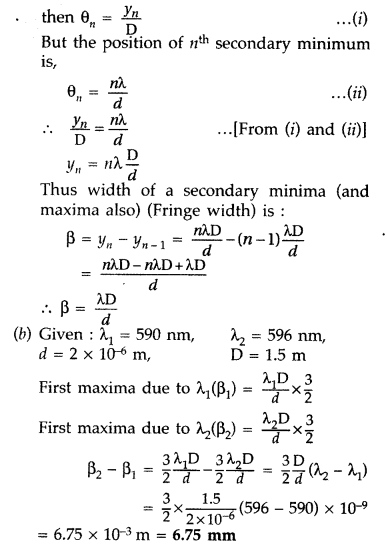
Question 101.
(a) Distinguish between linearly polarized and unpolarized light.
(b) Show that the light waves are transverse in nature.
(c) Why does light from a clear blue portion of the sky show a rise and fall of intensity when viewed through a polaroid which is rotated? Explain by drawing the necessary diagram. (Comptt. Delhi 2014)
Answer:
(a) Unpolarized light : A light wave, in which the electric vector oscillates in all possible directions in a plane perpendicular to the direction of propagation is known as unpolarized light.
Linearly polarized light : If the oscillations of the electric vectors are restricted to just one direction, in a plane perpendicular to the direction of propagation, the corresponding light is known as linearly polarized light.
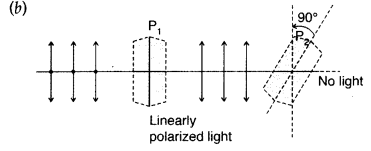
Unpolarized light passing through polaroid P
1
gets linearly polarized.
[As the electric field vector components parallel to the pass axis of P
1
are transmitted whereas the others are blocked.]
When this polarized light is incident on a polaroid P
2
, kept crossed with respect to P
1
, then these components also get blocked and no light is transmitted beyond P
2
.
(c) It is due to scattering of light by molecules of earth’s atmosphere.

Under the influence of the electric field of the incident (unpolarized) wave, the electrons in the molecules acquire components of motion in both these directions. Charges, accelerating parallel to the double arrows, do not radiate energy towards the observer since their acceleration has no transverse component.
The radiation scattered by the molecules is therefore represented by dots, i.e., it is polarized perpendicular to plane of figure.
Question 102.
(a) Using Huygen’s construction of secondary wavelets explain how a diffraction pattern is obtained on a screen due to a narrow slit on which a monochromatic beam of light is incident normally.
(b) Show that the angular width of the first diffraction fringe is half that of the central fringe.
(c) Explain why the maxima at \(\theta=\left(n+\frac{1}{2}\right) \frac{\lambda}{a}\) become weaker and weaker with increasing n. (Delhi 2014)
Answer:
(a) Diffraction Pattern : We can regard the total contribution of the wavefront LN at some point P on the screen, as the resultant effect of the superposition of its wavelets like LM, MM
2
, M
2
N. These have to be superposed taking into account their proper phase differences. We, therefore, get maxima and minima, i.e. a diffraction pattern, on the screen.
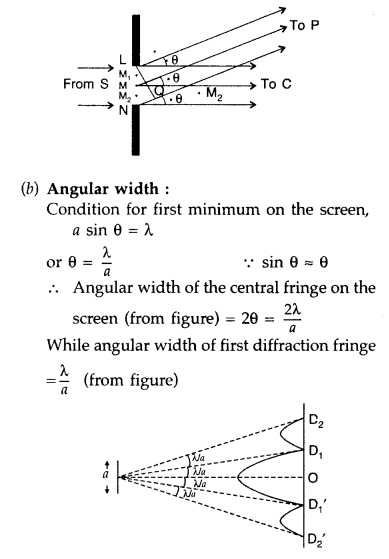
Hence angular width of first fringe is half of the angular width of central fringe.
(c) Maxima become weaker and weaker with increasing n. This is because the effective part of the wavefront, contributing to the maxima, becomes smaller and smaller, with increasing n.
Question 103.
(a) A point object ‘O’ is kept in a medium of refractive index n
1
in front of a convex spherical surface of radius of curvature R which separates the second medium of refractive index n
2
from the first one, as show in the figure.
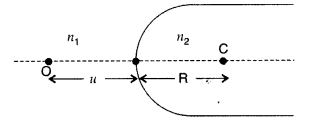
Draw the ray diagram showing the image formation and deduce the relationship between the object distance and the image distance in terms of n
1
, n
2
and R.
(b) When the image formed above acts as a virtual object for a concave spherical surface separating the medium n
2
from n
2
(n
2
> n
1
), draw this ray diagram and write the similar [similar to (a)] relation. Hence obtain the expression for the lens maker’s formula. (Delhi 2014)
Answer:
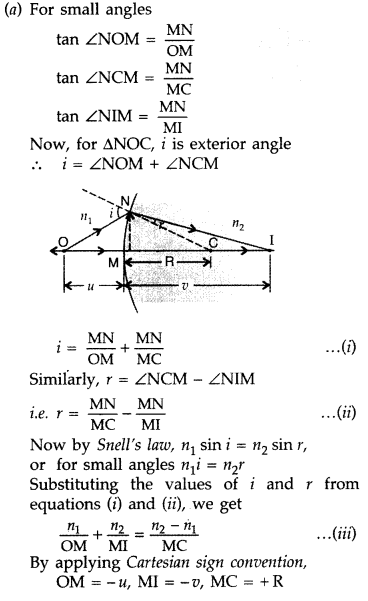
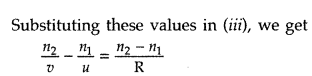
This equation gives us a relation between object and image distance in terms of refractive index of the medium and the radius of the curvature of the curved spherical surface. It holds for any curved spherical surface.
(b) Lens maker’s formula : Consider a thin double convex lens of refractive index n2 placed in a medium of refractive index n
2
Here n
1
< n
2
. Let B and D be the poles, C
1
and C
2
be the centres of curvature and R
1
and R
2
be the radii of curvature of the two lens surfaces ABC and ADC, respectively. For refraction at surface ABC, we can write the relation between the object distance v
1
, image distance v and radius of curvature R
1
as

Question 104.
(a) Consider two coherent sources S
1
and S
2
producing monochromatic waves to produce interference pattern. Let the displacement of the wave produced by S
1
be given by
Y
1
= a cos ωt
and the displacement by S
2
be Y
2
= a cos (ωt + ϕ )
Find out the expression for the amplitude of the resultant displacement at a point and show that the intensity at that point will be
![]()
Hence establish the conditions for constructive and destructive interference,
(b) What is the effect on the interference fringes in Young’s double slit experiment when
(i) the width of the source slit is increased;
(ii) the monochromatic source is replaced by a source of white light? (All India 2014)
Answer:

(b) (i) When width of the source slit is increased, then the angular fringe width remains unchanged, but fringes become less and less sharp, so visibility of fringes decreases. If the condition, \(\frac{s}{S}<\frac{\lambda}{d}\) is not satisfied, the interference pattern disappears.
(ii) When the monochromatic source is replaced by a source of white light, the interference pattern due to different component colours of white light overlap (incoherently). The central bright fringes for different colours are at the same position. Therefore, the central fringe is

Thus, the fringe closest on either side of the central white fringe is red and the farthest will appear blue. After a few fringes, no clear fringe pattern is seen.
Question 105.
(a) Define a wavefront. How is it different from a ray?
(b) Depict the shape of a wavefront in each of the following cases.
(i) Light diverging from point source.
(ii) Light emerging out of a convex lens when a point source is placed at its focus.
(iii) Using Huygen’s construction of secondary wavelets, draw a diagram showing the passage of a plane wavefront from a denser into a rarer medium. (Comptt. All India 2014)
Answer:
(a) Wavefront is the locus of all points, which oscillate in phase or it is the surface of constant phase.
A ray is defined as the path of energy propagation in the limit of wavelength tending to zero.
(b) Shapes of wave-front
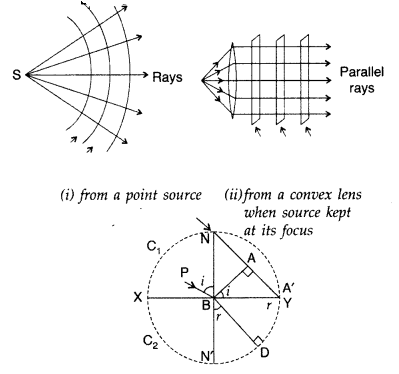
Question 106.
(i) In Young’s double slit experiment, deduce the condition for
(a) constructive,’ and
(b) destructive interference at a point on the screen. Draw a graph showing variation of intensity in the interference pattern against position ‘x’ on the screen.
(ii) Compare the interference pattern observed in Young’s double slit experiment with single slit diffraction pattern, pointing out three distinguishing features. (Delhi 2016)
Answer:
(i)
(a) For constructive interference : We will have constructive interference resulting in a bright fringe when path difference is equal to nλ.
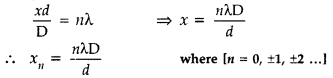
Since the separation between the centres of two consecutive bright fringes is called fringe width. It is denoted by β
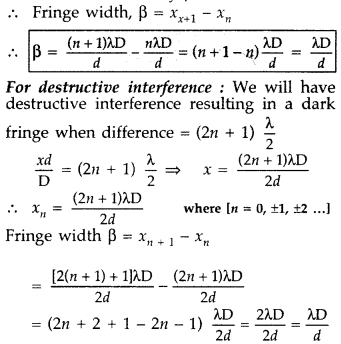
Hence all bright and dark fringes are of equal width.
Observations :
(i) Fringe width is directly proportional to the wavelength of light i.e. p X.
(ii) Fringe width is inversely proportional to the distance between two sources
![]()
(iii) Fringe width is directly proportional to the distance between screen and two sources i.e. \(\beta \propto \frac{1}{d}\).
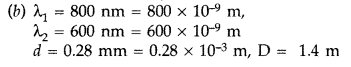
Suppose at any distance x from the central maximum,
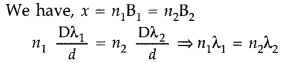
The bright fringes will coincide at the least distance x,
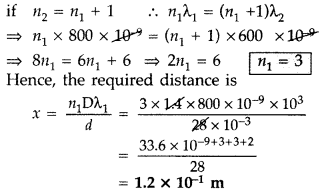
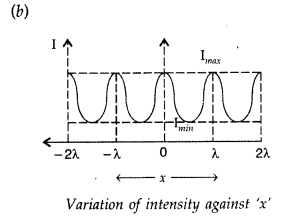
(ii)
Interference pattern and Diffraction pattern :
The diagram, given here, shows several fringes, due to double slit interference, ‘contained’ in a broad diffraction peak. When the separation between the slits is large compared to their width, the diffraction pattern becomes very flat and we observe the two slit interference pattern.

Basic features of distinction between interference and diffraction patterns :
(i) The interference pattern has a number of equally spaced bright and dark bands while diffraction pattern has a central bright maximum which is twice as wide as the other maxima.
(ii) Interference pattern is the superimposition of two waves slits originating from two narrow slits. The diffraction pattern is a superposition of a continuous family of waves originating from each point on a single slit.
(iii) For a single slit of width ‘a’ the first null of diffraction pattern occurs at an angle of \(\frac{\lambda}{a}\). At the same angle of \(\frac{\lambda}{a}\), we get a maxima for two narrow slits separated by a distance ‘a’.
Question 107.
(a) Draw a diagram showing the ‘Young’s arrangement’ for producing ‘a sustained interference pattern’. Hence obtain the expression for the width of the interference fringes obtained in this pattern.
(b) If the principal source point S were to be moved a little upwards, towards the slit S
1
from its usual symmetrical position, with respect to the two slits S
1
and S
2
, discuss how the interference pattern, obtained on the screen, would get affected. (Compt. Delhi 2016)
Answer:
(a)
Consider two coherent sources S
1
and S
2
separated by a distance d. Let D be the distance between the screen and the plane of slits S
1
and S
2
.
Light waves emitted from S
1
and S
2
reach point O on the screen after travelling equal distances. So path difference and hence phase difference between these waves is zero. Therefore, they meet at O in phase and hence constructive interference

takes place at O. Thus O is the position of the central bright fringe.
Let the waves emitted by S
1
and S
2
meet at point P and the screen at a distance y from the central bright fringe.
The path difference between these waves at P is given by

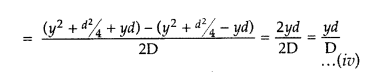
For constructive interference/maxima:
If path difference is an integral multiple of λ, then bright fringe will be formed at P
![]()
…where [m = 1, 2, 3 …
which is the position of mth bright fringe from the central bright fringe.
Fringe width (β) : The distance between any two successive bright fringes (or successive fringes) is called fringe width.
![]()
Destructive interferencelMinima: If path difference is odd multiple of \(\lambda / 2\), then dark fringe is formed at P
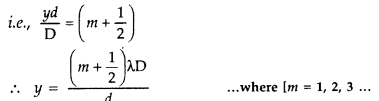
Which is position of m
th
dark fringe from the central bright fringe.
β(fringe width) = y
1
– y
0
![]()
(b) On shifting principal source point ‘S’ little upwards i.e. towards Sv the position of the central maximum on the screen will shift downwards on the screen, i.e. below its previous position. Hence, whole interference pattern will get shifted little downwards but fringe width will remain the same as that of . the initial arrangement.
Question 108.
Based on Huygen’s construction, draw the shape of a plane wavefront as it gets refracted on passing through a convex lens. (Comptt. All India 2016)
Answer:
The required shape of the wavefront is as shown
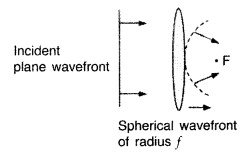
Question 109.
When a plane wave front, of light, of wavelength X, is incident on a narrow slit, an intensity distribution pattern, of the form shown is observed on a screen, suitably kept behind the slit. Name the phenomenon observed.
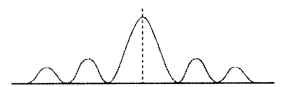
(a) Obtain the conditions for the formation of central maximum and secondary maxima and the minima.
(b) Why is there significant fall in intensity of the secondary maxima compared to the central maximum, where as in double slit experiment all the bright fringes are of the same intensity?
(c) When the width of the slit is made double the original width, how is the size of the central band affected? (Comptt. All India 2016)
Answer:
The phenomenon observed is the phenomenon of ‘diffraction’.
(a) At the central maximum : The contributions due to the secondary wavelets, from all parts of the wave front (at the slit), arrive in phase at the central maxima, At the central maxima θ = 0.
At the secondary maxima : It is only the contributions from (nearly) 1/3 (or 1/5, or 1/ 7, …) of the incident wavefront that do not get cancelled at the locations of the secondary maxima. These occur at points for which
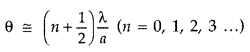
At the secondary minima : The contributions, from ‘corresponding pairs’, of the sub-parts of the incident wavefront, cancel each other and the net contribution, at the location of the minima, is zero. The minima occur at points for which
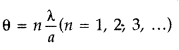
(b) There is a significant fall in intensity at the secondary maxima because the intensity there, is only due to the contribution of (nearly) (1/3 or 1/5 or 1/7, …) of the incident wavefronts.
(c) The size of the central maximum would get halved when width of the slit is doubled.
Question 110.
(a) Distinguish between unpolarised light and linearly polarised light. How does one get linearly polarised light with the help of a Polaroid?
(b) A narrow beam of unpolarised light of intensity I
0
is incident on a polaroid P
1
. The light transmitted by it is then incident on a second polaroid P
2
with its pass axis making angle of 60° relative to the pass axis of P
1
. Find the intensity of the light transmitted by P
2
. (Delhi 2016)
Answer:
(a) Distinction between unpolarised and polarised light: In an unpolarised light, the oscillations of the electric field, are in random directions, in planes perpendicular to the direction of propagation. For a polarised light, the oscillations are aligned along one particular direction.
Alternatively, Polarised light can be distinguished, from unpolarised light, when it is allowed to pass through a polaroid. Polarised light can show change in its intensity, on passing through a polaroid:
while intensity of transmitted light will remain unchanged in case of unpolarised light.
Polarised light with the help of a polaroid : When unpolarised light wave is incident on a polaroid, the electric vectors along the, direction of its aligned molecules get absorbed; the electric vector, oscillating along a direction perpendicular to the aligned molecules, pass through. This light is called linearly polarised light.

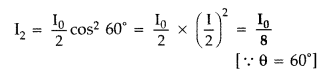
Question 111.
(a) Explain two features to distinguish between the interference pattern in Young’s double slit experiment with the diffraction pattern obtained due to a single slit.
(b) A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young’s double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit. (Delhi. 2016)
Answer:
(a) Interference pattern and Diffraction pattern :
The diagram, given here, shows several fringes, due to double slit interference, ‘contained’ in a broad diffraction peak. When the separation between the slits is large compared to their width, the diffraction pattern becomes very flat and we observe the two slit interference pattern.

Basic features of distinction between interference and diffraction patterns :
(i) The interference pattern has a number of equally spaced bright and dark bands while diffraction pattern has a central bright maximum which is twice as wide as the other maxima.
(ii) Interference pattern is the superimposition of two waves slits originating from two narrow slits. The diffraction pattern is a superposition of a continuous family of waves originating from each point on a single slit.
(iii) For a single slit of width ‘a’ the first null of diffraction pattern occurs at an angle of \(\frac{\lambda}{a}\). At the same angle of \(\frac{\lambda}{a}\), we get a maxima for two narrow slits separated by a distance ‘a’.

Question 112.
(a) Define wavefront. Use Huygens’ principle to verify the laws of refraction.
(b) How is linearly polarised light obtained by the process of scattering of light? Find the Brewster angle for air—glass interface, when the refractive index of glass = 1.5. (All India 2016)
Answer:
(a) Wavefront : The wavefront is the common locus of all points which are in phase (surface of constant phase)
Huygens’ principle to verify laws of refraction :
Huygens’ geometrical construction for a plane wave propagation. Let AB be a section of primary wavefront at any instant t. Take points 1, 2, 3, 4, … on the wavefront AB. Taking each point as centre, draw spheres of radius r = ct, where c is the velocity of light in the medium.
Draw a surface A
1
B
1
touching tangentially at the secondary wavelets in the forward direction. The surface A
1
B
1
is the secondary wavefront after time t.

A surface A
2
B
2
touching tangentially all the secondary wavelets in the backward direction can be drawn to give a backward secondary wavefront.
Laws of refraction using Huygen’s principle. Let XY be the refracting surface separating two mediums 1
st
and 2
nd
. Let c
1
and c
2
be the velocities of light in these mediums.

Let AB be a plane wavefront moving through the surface XY meeting at the point B.
The time taken ‘t’ of A to reach at A’B then

To obtain new front, draw a circle with point B as centre and BD as radius in 2nd medium. Draw a tangent A’D from point A’. Then A’D represents the refracted wavefront.
Since PB be incident ray and BD be refracted ray

This constant V is called the refractive index of material which proves Snell’s law of refraction.
(b) When unpolarised light gets scattered by molecules of earth’s atmosphere, the scattered light has only one of its two components in it and hence linearly polarised, as shown in the diagram :
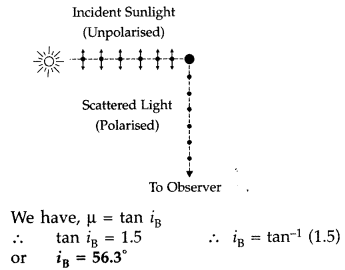
Question 113.
Explain with diagram, how plane polarized light can be produced by scattering of sunlight. An incident beam of light of intensity IG is made to fall on a polaroid A. Another polaroid B is so oriented with respect to A that there is no light emerging out of B. A third polaroid C is now introduced mid-way between A and B and is so oriented that its axis bisects the angle between the axes of A and B. Calculate the intensity of light transmitted by A, B and C. (Comptt. Delhi 2016)
Answer:
(i) (c) It is due to scattering of light by molecules of earth’s atmosphere.

Under the influence of the electric field of the incident (unpolarized) wave, the electrons in the molecules acquire components of motion in both these directions. Charges, accelerating parallel to the double arrows, do not radiate energy towards the observer since their acceleration has no transverse component.
The radiation scattered by the molecules is therefore represented by dots, i.e., it is polarized perpendicular to plane of figure.
Question 114.
(a) In Young’s double slit experiment a monochromatic source of light S is kept equidistant from the slits S2 and S2. Explain the formation of dark and bright fringes on the screen.
(b) A beam of light consisting of two wavelengths, 650 nm and 520 nm, is used to obtain interference fringes in Young’s double-slit experiment.
(i) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 650 nm?
(ii) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide?
Given : the separation between the slits is 4 mm and the distance between the screen and plane of the slits is 1.2 m. (Comptt. Delhi 2016)
Answer:
(a) Young’s double slit experiment. The path difference between two rays coming from holes S
1
and S
2
is (S
2
P – S
1
P). If point P corresponds to a maximum,

If x, d << D, then negligible error will be introduced if (S
2
P + S
1
P) in the denominator is replaced by 2D.

Thus, bright and dark bands appear on the screen. Such bands are called ‘fringes’.
These dark and bright fringes are equally spaced.

