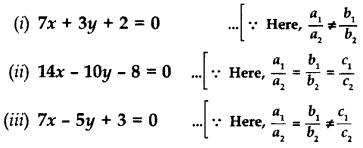Important Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
Pair of Linear Equations in Two Variables Class 10 Important Questions Very Short Answer (1 Mark)
Question 1.
How many solutions does the pair of equations y = 0 and y = -5 have? (2013)
Solution:
y = 0 and y = -5 are Parallel lines, hence no solution.
Question 2.
If ax + by = a
2
– b
2
and bx + ay = 0, find the value of (x + y). (2013)
Solution:
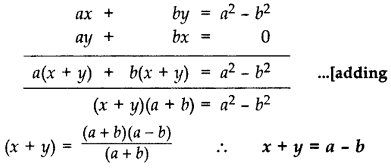
Question 3.
For what value of k, the pair of equations 4x – 3y = 9, 2x + ky = 11 has no solution? (2017D)
Solution:
We have, 4x – 3y = 9 and 2x + ky = 11
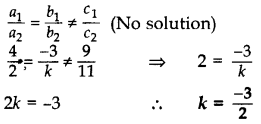
Question 4.
Calculate the area bounded by the line x + y = 10 and both the co-ordinate axes. (2012)
Solution:
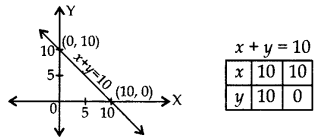
Area of triangle
= \(\frac{1}{2}\) × base × corresponding altitude
= \(\frac{1}{2}\) × 10 × 10 = 50 cm
2
Pair of Linear Equations in Two Variables Class 10 Important Questions Short Answer-1 (2 Marks)
Question 5.
Find whether the following pair of linear equations is consistent or inconsistent: (2015)
3x + 2y = 8 6x – 4y = 9
Solution:
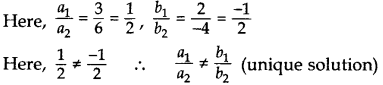
Therefore, given pair of linear equations is con-sistent.
Question 6.
Check graphically whether the pair of equations 3x – 2y + 2 = 0 and \(\frac{3}{2}\)x – y + 3 = 0, is consistent. Also find the coordinates of the points where the graphs of the equations meet the Y-axis.
Solution:
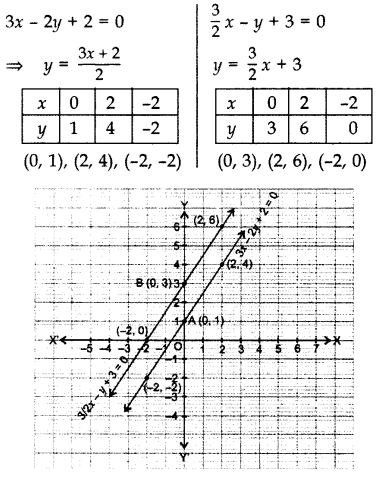
By plotting the points and joining them, the lines do not intersect anywhere, i.e., they are parallel.
Therefore given pair of equations is not consistent, i.e., inconsistent.
The equation 3x – 2y + 2 = 0 meets the Y-axis at A(0,1).
The equation \(\frac{3}{2}\)x – y + 3 = 0 meets the Y-axis at B(0, 3).
Question 7.
Draw the graph of
2y = 4x – 6; 2x = y + 3 and determine whether this system of linear equations has a unique solution or not.
Solution:
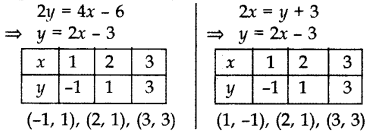
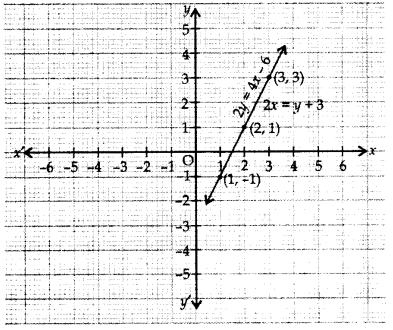
Since both the lines coincide.
Therefore infinitely many solutions.
Question 8.
Represent the following pair of equations graphically and write the coordinates of points where the lines intersect y-axis.
Solution:
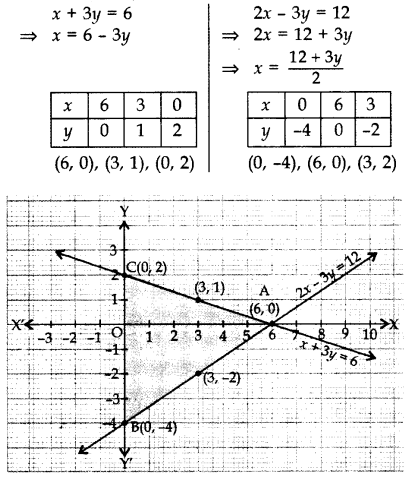
By plotting the points and joining them, the lines intersect at A (6, 0).
Line x + 3y = 6 intersects y-axis at B(0, 2) and Line 2x – 3y = 12 intersects y-axis at C(0, -4).
Pair of Linear Equations in Two Variables Class 10 Important Questions Short Answer-II (3 Marks)
Question 9.
Solve the following pair of equations for x and y: (2012)
\(\frac{a^{2}}{x}-\frac{b^{2}}{y}\) = 0; \(\frac{a^{2} b}{x}+\frac{b^{2} a}{y}\) = a + b, x ≠ 0; y ≠ 0
Solution:

Question 10.
Solve for x and y:
\(\frac{10}{x+y}+\frac{2}{x-y}=4 ; \quad \frac{15}{x+y}-\frac{5}{x-y}=-2\)
x + y ≠ 0
x – y ≠ 0 (2012, 2017D)
Solution:
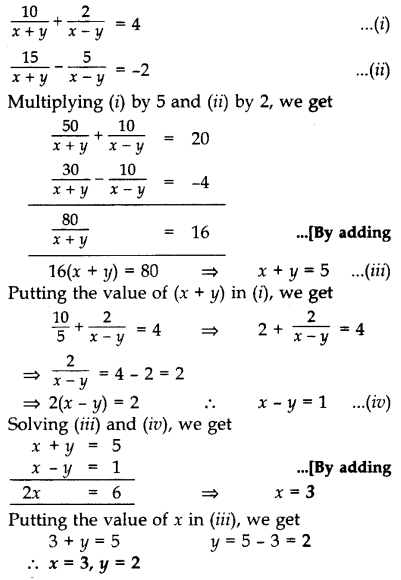
Question 11.
Solve the following pair of linear equations for x and y:
141x + 93y = 189;
93x + 141y = 45 (2013)
Solution:

Question 12.
Solve the following pair of linear equations for x and y: (2013)
\(\frac{b}{a} x+\frac{a}{b} y\) = a
2
+ b
2
; x + y = 2ab
Solution:

Question 13.
Solve by elimination: (2014)
3x = y + 5
5x – y = 11
Solution:
We have, 3x = y + 5, and 5x – y = 11

Putting the value of x in (i), we get
3x – y = 5 ⇒ 3(3) – y = 5
9 – 5 = y ⇒ y = 4
∴ x = 3, y = 4
Question 14.
Solve by elimination: 2015
3x – y – 7
2x + 5y + 1 = 0
Solution:
3 x – y = 7 …(i)
2x + 5y = -1 -00
Multiplying equation (i) by 5 & (ii) by 1,
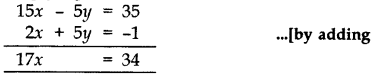
⇒ x = 2
Putting the value of x in (i), we have
3(2)-y = 7 ⇒ 6 – 7 = y
∴ y = -1 ∴ x = 2, y = -1
Question 15.
Solve for x and y: (2017OD)
27x + 31y = 85;
31x + 2 7y = 89
Solution:

Putting the value of ‘x’ in (i), we get
2 + y = 3 ⇒ y = 3 – 2 = 1
∴ x = 2, y = 1
Question 16.
Solve for x and y: \(\frac{x}{a}=\frac{y}{b}\);
ax + by = a
2
+ b
2
(2017D)
Solution:
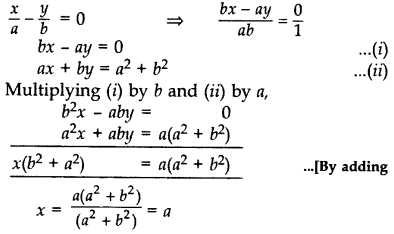
Putting the value of x in (i), we get
b(a) – ay = 0 ⇒ ba = ay
\(\frac{b a}{a}\) = y ∴ b = y
∴ x = a, y = b
Question 17.
Solve: \(\frac{x}{a}+\frac{y}{b}\) = a + b; \(\frac{x}{a^{2}}+\frac{y}{b^{2}}\) =2, a, b ≠ 0 (2017OD)
Solution:
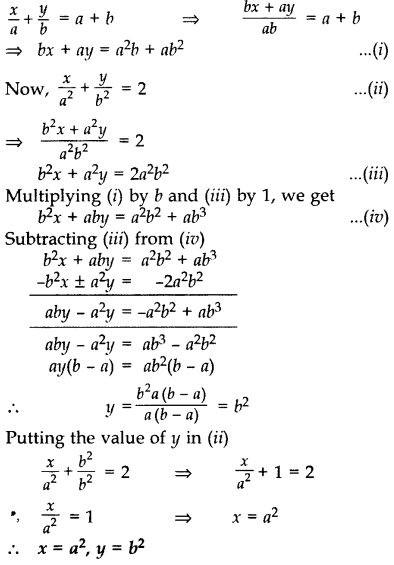
Question 18.
Solve the following pair of equations: (2014)
49x + 51y = 499
51x + 49 y = 501
Solution:

Question 19.
Find the two numbers whose sum is 75 and difference is 15. (2014)
Solution:
Let the two numbers be x and y.
According to the question,
x + y = 75 …(i)
∴ x – y = ±15 …(ii)
Solving (i) and (ii), we get
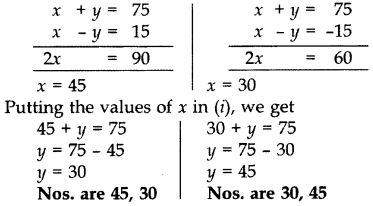
Question 20.
Find the value of a and p for which the following pair of linear equations has infinite number of solutions:
2x + 3y = 7;
αx + (α + β)y = 28 (2013)
Solution:
We have, 2x + 3y = 7 and αx + (α + β)y = 28
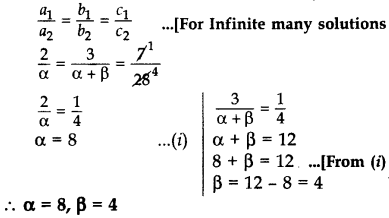
Question 21.
Solve the following pair of linear equations by the cross multiplication method: x + 2y = 2; x – 3y = 7 (2015)
Solution:
x + 2y – 2 = 0
x – 3y – 7 = 0
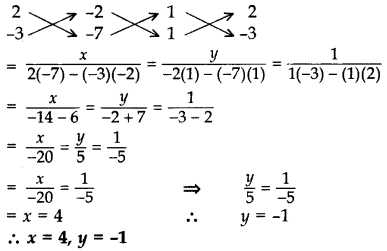
Question 22.
A man earns ₹600 per month more than his wife. One-tenth of the man’s salary and l/6
th
of the wife’s salary amount to ₹1,500, which is saved every month. Find their incomes. (2014)
Solution:
Let wife’s monthly income = ₹x
Then man’s monthly income = ₹(x + 600)
According to the question,
\(\frac{1}{10}\) (x + 600) + \(\frac{1}{6}\) (x) = ₹1,500
\(\frac{3(x+600)+5 x}{30}\) = ₹1,500
3x + 1,800 + 5x = ₹45,000
8x = ₹45,000 – ₹1,800
x = ₹\(\frac{343,200}{8}\) = ₹5,400
Wife’s income = ₹x = ₹5,400
Man’s income = ₹(x + 600) = ₹6,000
Question 23.
The sum of the digits of a two digit number is 8 and the difference between the number and that formed by reversing the digits is 18. Find the number. (2015)
Solution:
Let unit and tens digit be x and y.
∴ Original number = 1x + 10y …(i)
Reversed number = 10x + 1y
According to question,
x + y = 8
⇒ y = 8 – x …(ii)
Also, 1x + 10Oy – (10x + y) = 18
⇒ x + 10y – 10x – y = 18
⇒ 9y – 9x = 18
⇒ y – x = 2 …[Dividing both sides by 9
⇒ 8 – x – x = 2 …[From (it)
⇒ 8 – 2 = 2x
⇒ 2x = 6
From (it), y = 8 – 3 = 5
From (i), Original number = 3 + 10(5) = 53
Pair of Linear Equations in Two Variables Class 10 Important Questions Long Answer (4 Marks)
Question 24.
The age of the father is twice the sum of the ages of his 2 children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father. (2012)
Solution:
Let the present ages of his children be x years and y years.
Then the present age of the father = 2(x + y) …(i)
After 20 years, his children’s ages will be
(x + 20) and (y + 20) years
After 20 years, father’s age will be 2(x + y) + 20
According to the Question,
⇒ 2(x + y) + 20 = x + 20 + y + 20
⇒ 2x + 2y + 20 = x + y + 40
⇒ 2x + 2y – x – y = 40 – 20
⇒ x + y = 20 …[From (i)
∴ Present age of father = 2(20) = 40 years
Question 25.
A two digit number is seven times the sum of its digits. The number formed by reversing the digits is 18 less than the given number. Find the given number. (2013)
Solution:
Let unit’s place digit be x and ten’s place digit bey.
Then original number = x + 10y
and reversed number = 10x + y
According to the Question,
x + 10y = 7(x + y)
x + 10y = 7x + 7y
⇒ 10y – 7y = 7x – x
⇒ 3y = 6x ⇒ y = 2x …(i)
(x + 10y) – (10x + y) = 18
x + 10y – 10x – y = 18
⇒ 9y – 9x = 180
⇒ y – x = 2 …[Dividing by 9
⇒ 2x – x = 2 …[From (i)
∴ x = 2
Putting the value of ‘x’ in (i), we get y = 2(2) = 4
∴ Required number = x + 10y
= 2 + 10(4) = 42
Question 26.
Sita Devi wants to make a rectangular pond on the road side for the purpose of providing drinking water for street animals. The area of the pond will be decreased by 3 square feet if its length is decreased by 2 ft. and breadth is increased by 1 ft. Its area will be increased by 4 square feet if the length is increased by 1 ft. and breadth remains same. Find the dimensions of the pond. (2014)
Solution:
Let length of rectangular pond = x
and breadth of rectangular pond = y
Area of rectangular pond = xy
According to Question,
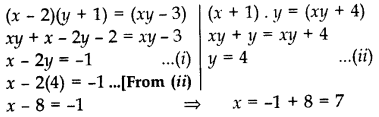
∴Length of rectangular pond = 7 ft.
Breadth of rectangular pond = 4 ft.
Question 27.
On reversing the digits of a two digit number, number obtained is 9 less than three times the original number. If difference of these two numbers is 45, find the original number. (2014)
Solution:
Let unit’s place digit be x and ten’s place digit bey.
∴ Original number = x + 10y Reversed number = 10x + y
According to the Question,
10x + y = 3(x + 10y) – 9
⇒ 10x + y = 3x + 30y – 9
⇒ 10x + y – 3x – 30y = -9
⇒ 7x – 29y = -9 …(i)
10x + y – (x + 10y) = 45
⇒ 9x – 9y = 45
⇒ x – y = 5 …[Dividing both sides by 9
⇒ x – 5 + y …(ii)
Solving (i),
7x – 29y = -9
7(5 + y) – 29y = -9 …[From (ii)
35+ 7y – 29y = -9
-22y = -9 – 35
-22y = -44 ⇒ y = \(\frac{44}{22}\) = 2
Putting the value of y in (ii),
x = 5 + 2 = 7
∴ Original number = x + 10y
= 7 + 10(2) = 27
Question 28.
Speed of a boat in still water is 15 km/h. It goes 30 km upstream and returns back at the same point in 4 hours 30 minutes. Find the speed of the stream. 2017D
Solution:
Let the speed of the stream = x km/hr
Speed of the boat in still water = 15 km/hr
then, the speed of the boat upstream = (15 – x) km/hr
and the speed of the boat downstream = (15 + x) km/hr

∴ Speed of stream = 5 km/hr
Question 29.
The owner of a taxi company decides to run all the taxis on CNG fuel instead of petrol/diesel. The taxi charges in city comprises of fixed charges together with the charge for the distance covered. For a journey of 12 km, the charge paid is 789 and for journey of 20 km, the charge paid is ₹145.
What will a person have to pay for travelling a distance of 30 km? (2014)
Solution:
Let the fixed charges = 7x
and the charge per km = ₹y
According to the Question,
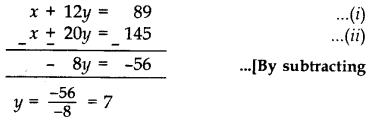
Putting the value of y in (i), we get
x + 12(7) = 89
x + 84 = 89 ⇒ x = 89 – 84 = 5
Total fare for 30 km = x + 30y = 5 + 30(7)
= 5 + 210 = ₹215
Question 30.
A boat takes 4 hours to go 44 km downstream and it can go 20 km upstream in the same time. Find the speed of the stream and that of the boat in still water. (2015)
Solution:
Let the speed of the stream = y km/hr
Let the speed of boat in still water = x km/hr
then, the speed of the boat in downstream = (x + y) km/hr
and, the speed of the boat in upstream = (x – y) km/hr
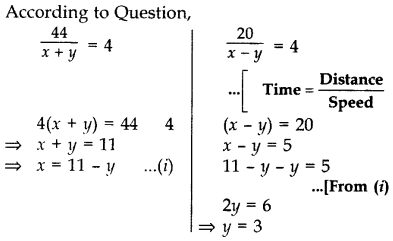
From (i), x = 11 – 3 = 8
∴ Speed of the stream, y =3 km/hr
Speed of the boat in still water, x = 8 km/hr
Question 31.
A man travels 300 km partly by train and partly by car. He takes 4 hours if the travels 60 km by train and the rest by car. If he travels 100 km by train and the remaining by car, he takes 10 minutes longer. Find the speeds of the train and the car separately. (2017D)
Solution:
Let the speed of the train = x km/hr
Let the speed of the car = y km/ hr
According to the Question,

∴ Speed of the train = 60 km/hr
and Speed of the car = 80 kn/hr
Question 32.
The owner of a taxi company decides to run all the taxis on CNG fuel instead of petrol/diesel. The taxi charges in city comprises of fixed charges together with the charge for the distance covered. For a journey of 13 km, the charge paid is ₹129 and for a journey of 22 km, the charge paid is ₹210.
What will a person have to pay for travelling a distance of 32 km? (2014 )
Solution:
Let fixed charge be ₹x and the charge for the distance = ₹y per km
According to the Question,
For a journey of 13 km,
x + 13y = 129 ⇒ x = 129 – 13y …(/)
For a journey of 22 km, x + 22y = 210 …(ii)
⇒ 129 – 13y + 22y = 210 …[From (i)
⇒ 9y = 210 – 129 = 81
⇒ 9y = 81 ⇒ y = 9
From (i), x = 129 – 13(9)
= 129 – 117 = 12
∴ Fixed charge, x = ₹12
∴ The charge for the distance, y = ₹9 per km
To pay for travelling a distance of 32 km
= x + 32y = 12 + 32(9) = 12 + 288 = ₹300
Question 33.
Solve the following pair of linear equations graphically:
x + 3y = 6 ; 2x – 3y = 12
Also find the area of the triangle formed by the lines representing the given equations with y-axis. (2012, 2015)
Solution:
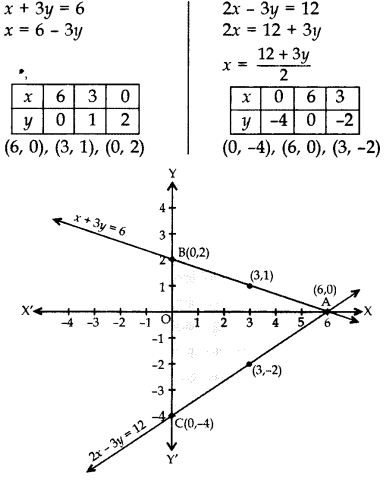
By plotting points and joining them, the lines intersesct at A(6, 0)
∴ x = 6, y = 0
Line x + 3y = 6 intersects Y-axis at B(0, 2) and Line 2x – 3y = 12 intersects Y-axis at C(0, -4). Therefore, Area of triangle formed by the lines with y-axis.
Area of triangle
= \(\frac{1}{2}\) × base × corresponding altitude
= \(\frac{1}{2}\) × BC × AO = \(\frac{1}{2}\) × 6 × 6 = 18 sq. units
Question 34.
Draw the graphs of following equations:
2x – y = 1; x + 2y = 13
Find the solution of the equations from the graph and shade the triangular region formed by the lines and the y-axis. (2013)
Solution:
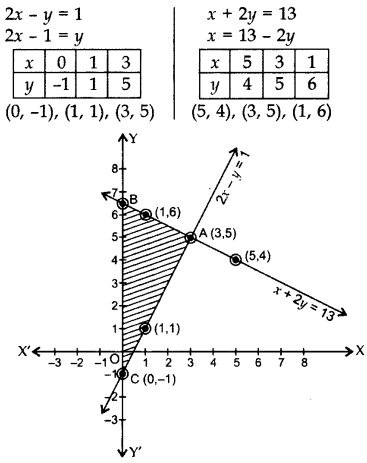
By plotting the points and joining them, the lines intersect at A(3,5).
∴ x = 3, y = 5
Here ∆ABC is the required triangle.
Question 35.
Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and x-axis. (2012, 2017D)
Solution:
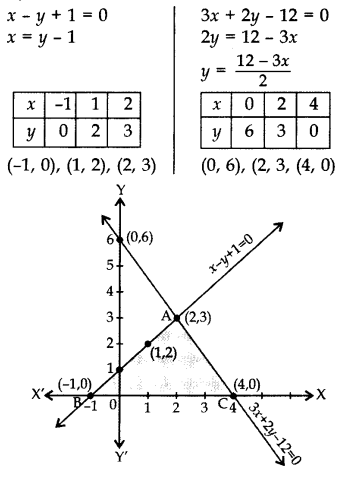
Lines intersect at (2, 3)
∴ x = 2, y = 3
Vertices of ∆ABC are A(2, 3), B(-1, 0) and C(4, 0)
Question 36.
Amit bought two pencils and three chocolates for ₹11 and Sumeet bought one pencil and two chocolates for ₹7. Represent this situation in the form of a pair of linear equations. Find the price of one pencil and that of one chocolate graphically. (2017OD)
Solution:
Let the price of one pencil = ₹x and the price of one chocolate = ₹y.
As per the Question,
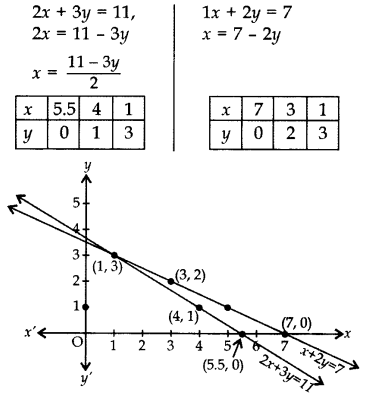
Lines intersect at (1, 3).
∴ x = 1, y = 3
Therefore the price of one pencil = ₹1 and price of one chocolate = ₹3
Question 37.
7x – 5y – 4 = 0 is given. Write another linear equation, so that the lines represented by the pair are:
(i) intersecting
(ii) coincident
(iii) parallel (2015 OD)
Solution:
7x – 5y – 4 = 0