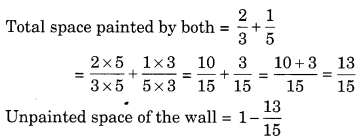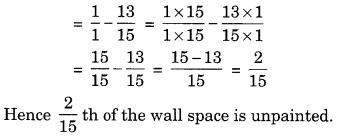Class 6 Maths Chapter 7 Extra Questions Fractions
Class 6 Maths Fractions Extra Questions
NCERT Class 6 Maths Chapter 7 Fractions Extra Questions and Answers
Question 1.
Match each fractional unit with the correct picture.

Solution:
(a) – (ii),
(b) – (iii),
(c) – (iv),
(d) – (i)
Question 2.
Shade the parts of the figures according to the given fraction.
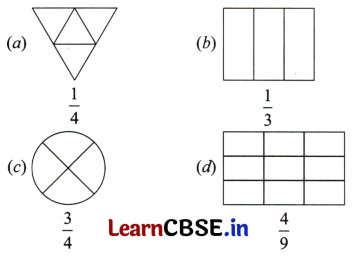
Solution:
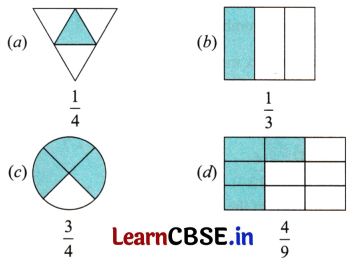
![]()
Question 3.
Write the following fractions as mixed fractions.
(a) \(\frac{8}{3}\)
(b) \(\frac{12}{7}\)
(c) \(\frac{25}{9}\)
Solution:
(a) \(\frac{8}{3}\) = 2 + \(\frac{2}{3}\) = 2\(\frac{2}{3}\)
(b) \(\frac{12}{7}\) = 1 + \(\frac{5}{7}\) = 1\(\frac{5}{7}\)
(c) \(\frac{25}{9}\) = 2 + \(\frac{7}{9}\) = 2\(\frac{7}{9}\)
Question 4.
Express the following mixed fractins as improper fractions:
(a) 1\(\frac{3}{5}\)
(b) 6\(\frac{1}{8}\)
(c) 3\(\frac{1}{7}\)
(d) 1\(\frac{1}{4}\)
Solution:
(a) 1\(\frac{3}{5}\) = 1 + \(\frac{3}{5}\) = \(\frac{(1 \times 5)+3}{5}\) = \(\frac{5+3}{5}\) = \(\frac{8}{5}\)
(b) 6\(\frac{1}{8}\) = 6 + \(\frac{1}{8}\) = \(\frac{(6 \times 8)+1}{8}\) = \(\frac{48+1}{8}\) = \(\frac{49}{8}\)
(c) 3\(\frac{1}{7}\) = 3 + \(\frac{1}{7}\) = \(\frac{(3 \times 7)+1}{7}\) = \(\frac{21+1}{7}\) = \(\frac{22}{7}\)
(a) 1\(\frac{1}{4}\) = 1 + \(\frac{1}{4}\) = \(\frac{(1 \times 4)+1}{4}\) = \(\frac{4+1}{4}\) = \(\frac{5}{4}\)
Question 5.
Figure out the number of whole units in each of the following fractions.
(a) \(\frac{9}{5}\)
(b) \(\frac{7}{3}\)
(c) \(\frac{31}{8}\)
Solution:
(a) \(\frac{9}{5}\) = 1 + \(\frac{4}{5}\) = 1\(\frac{4}{5}\)
Here, the number of whole unit is 1.
(b) \(\frac{7}{3}\) = 2 + \(\frac{1}{3}\) = 2\(\frac{1}{3}\)
Here, the number of whole units is 2.
(c) \(\frac{31}{8}\) = 2 + \(\frac{1}{3}\) = 2\(\frac{1}{3}\)
Here, the number of whole units is 3.
Question 6.
Replace the box in

by the correct number.
Solution:
Since, 42 ÷ 6 = 7
∴ 84 ÷ 7 = 12 ⇒ \(\frac{42 \div 7}{84 \div 7}\) = \(\frac{6}{12}\)
Thus, \(\frac{42}{84}\) = \(\frac{6}{12}\)
Question 7.
Check whether the fractions \(\frac{5}{12}\) and \(\frac{30}{84}\) are equivalent or not.
Solution:
Let us have the cross multiplication of \(\frac{5}{17}\) and \(\frac{30}{84}\).

i.e. 420 ≠ 510 ⇒ [Both the products are different]
∴ The fractions are not equivalent.
Question 8.
Reduce the fraction \(\frac{40}{80}\) to its lowest term.
Solution:
The given fraction = \(\frac{48}{80}\)
First let us find the HCF of 48 and 80,

Now, dividing both the numerator and denominator by 16, we have \(\frac{48 \div 16}{80 \div 16}\) \(=\frac{3}{5}\)
∵ 3 and 5 have no common factor other than 1, i.e., \(\frac{3}{5}\) is in its lowest term.
∴ The lowest term of \(\frac{48}{80}\) is \(\frac{3}{5}\).
![]()
Question 9.
Arrange \(\frac{5}{6}\), \(\frac{1}{2}\), \(\frac{2}{3}\) and \(\frac{8}{9}\) in ascending order.
Solution:
Since, all the given fractions are unlike fractions.
∴ First, we convert them into equivalent fractions.
The denominators of the given fraction will be the LCM of 6, 2, 3 and 9.
Let us find the LCM of 6, 2, 3 and 9.

Now, let us write the equivalent fractions of the given fractions with denominator 18.

Question 10.
Write these fractions appropriately as additions or subtractions.

Solution:
(a) \(\frac{5}{5}\) – \(\frac{3}{5}\) = \(\frac{2}{5}\)
(b) \(\frac{2}{6}\) + \(\frac{3}{6}\) = \(\frac{5}{6}\)
(c) \(\frac{1}{5}\) + \(\frac{2}{5}\) = \(\frac{3}{5}\)
(d) \(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\)
Question 11.
Five balls together weigh 1 kg. If they are roughly the same size, then what is the weight of each ball?
Solution:
Total weight of five balls = 1 kg.
Therefore, the weight of each ball = \(\frac{1}{5}\) kg.
![]()
Question 12.
Add the following fractions by using Brahmagupta’s method:
(a) \(\frac{1}{3}\) and \(\frac{3}{5}\)
(b) \(\frac{2}{7}\) and \(\frac{4}{9}\)
(c) \(\frac{5}{6}\) and \(\frac{1}{2}\)
Solution:
(a) The denominators of the given fractions are 3 and 5.
The LCM of 3 and 5 is 15.
Then, \(\frac{1}{3}\) = \(\frac{1 \times 5}{3 \times 5}\) = \(\frac{5}{15}\) and \(\frac{3}{5}\) = \(\frac{3 \times 3}{5 \times 3}\) = \(\frac{9}{15}\)
Therefore, \(\frac{1}{3}\) + \(\frac{3}{5}\) = \(\frac{5}{15}\) + \(\frac{9}{15}\) = \(\frac{14}{15}\)
(b) The denominators of the given fractions are 7 and 9.
The LCM of 7 and 9 is 63.
Then, \(\frac{2}{7}\) = \(\frac{2 \times 9}{7 \times 9}\) = \(\frac{18}{63}\) and \(\frac{4}{9}\) = \(\frac{4 \times 7}{9 \times 7}\) = \(\frac{28}{63}\)
Therefore, \(\frac{2}{7}+\frac{4}{9}\) = \(\frac{18}{63}+\frac{28}{63}\) = \(\frac{46}{63}\)
(c) The denominators of the given fractions are 6 and 2.
The LCM of 6 and 2 is 6.
Then, \(\frac{5}{6}\) = \(\frac{5 \times 1}{6 \times 1}\) = \(\frac{5}{6}\) and \(\frac{1}{2}\) = \(\frac{1 \times 3}{2 \times 3}\) = \(\frac{3}{6}\)
Therefore, \(\frac{5}{6}+\frac{1}{2}\) = \(\frac{5}{6}+\frac{3}{6}\) = \(\frac{8}{6}\) = \(\frac{4}{3}\)
Question 13.
Subtract the following fractions by using Brahmagupta’s method:
(a) \(\frac{3}{5}\) – \(\frac{1}{2}\)
(b) \(\frac{2}{3}\) – \(\frac{1}{7}\)
(c) \(\frac{1}{8}\) – \(\frac{1}{9}\)
Solution:
(a) The denominators of the given fractions are 2 and 5. LCM of 2 and 5 is 10.
Then, \(\frac{1}{2}\) = \(\frac{1 \times 5}{2 \times 5}\) = \(\frac{5}{10}\) and \(\frac{3}{5}\) = \(\frac{3 \times 2}{5 \times 2}\) = \(\frac{6}{10}\)
Therefore, \(\frac{3}{5}\) – \(\frac{1}{2}\) = \(\frac{6}{10}\) – \(\frac{5}{10}\) = \(\frac{1}{10}\)
(b) The denominators of the given fractions are 3 and 7.
LCM of 3 and 7 is 21.
Then, \(\frac{2}{3}\) = \(\frac{2 \times 7}{3 \times 7}\) = \(\frac{14}{21}\) and \(\frac{1}{7}\) = \(\frac{1 \times 3}{7 \times 3}\) = \(\frac{3}{21}\)
Therefore, \(\frac{2}{3}\) – \(\frac{1}{7}\) = \(\frac{14}{21}\) – \(\frac{3}{21}\) = \(\frac{11}{21}\)
(c) The denominators of the given fractions are 8 and 9. LCM of 8 and 9 is 72.
Then \(\frac{1}{8}\) = \(\frac{1 \times 9}{8 \times 9}\) = \(\frac{9}{72}\) and \(\frac{1}{9}\) = \(\frac{1 \times 8}{9 \times 8}\) = \(\frac{8}{72}\)
Therefore, \(\frac{1}{8}\) – \(\frac{1}{9}\) = \(\frac{9}{72}\) – \(\frac{8}{72}\) = \(\frac{1}{72}\)
Question 14.
A bag of wheat weighs \(\frac{5}{2}\) kg. Another bag of rice weighs \(\frac{9}{4}\) kg. What is the total weight of the two bags?
Solution:
Weight of a bag of wheat = \(\frac{5}{2}\) kg
Weight of a bag of rice = \(\frac{9}{4}\) kg
Total weight = (\(\frac{5}{2}\) + \(\frac{9}{4}\)) kg
The denominators of the given fractions are 2 and 4.
∴ The LCM of 2 and 4 is 4.
Then, \(\frac{5}{2}\) = \(\frac{5 \times 2}{2 \times 2}\) = \(\frac{10}{4}\) and \(\frac{9}{4}\) = \(\frac{9 \times 1}{4 \times 1}\) = \(\frac{9}{4}\)
Therefore, \(\frac{5}{2}\) + \(\frac{9}{4}\) = \(\frac{10}{4}\) + \(\frac{9}{4}\) = \(\frac{19}{4}\)
Hence, the weight of the two bags is \(\frac{19}{4}\) = 4\(\frac{4}{3}\) kg.
![]()
Question 15.
Rahul takes \(\frac{11}{7}\) hours to finish his homework while Naman takes \(\frac{15}{8}\) hours to finish his homework. Who takes more time and by how much?
Solution:
Time taken by Rahul to finish his homework = \(\frac{11}{7}\) hours
Time taken by Naman to finish his homework = \(\frac{15}{8}\) hours
The difference in the time taken by the two = (\(\frac{15}{8}\) – \(\frac{11}{7}\)) jours
The denominators of the given fractions are 8 and 7.
∴ The LCM of 8 and 7 is 56.
Then, \(\frac{15}{8}\) = \(\frac{15 \times 7}{8 \times 7}\) = \(\frac{105}{56}\) and \(\frac{11}{7}\) = \(\frac{11 \times 8}{7 \times 8}\) = \(\frac{88}{56}\)
Therefore, \(\frac{15}{8}-\frac{11}{7}\) = \(\frac{105}{56}-\frac{88}{56}\) = \(\frac{17}{56}\)
Hence, Naman takes \(\frac{17}{56}\) hours more than Rahul to finish his homework.
Fractions Class 6 Extra Questions Very Short Answer Type
Question 1.
Represent the following fractions on number line.
![]()
Solution:
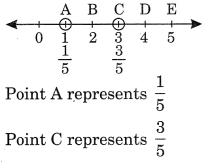
Question 2.
Write the fractions showing the shaded portions:
Solution:
(a) Shaded portion represents \(\frac { 1 }{ 4 }\)
Shaded portion represents \(\frac { 2 }{ 6 }\)
Question 3.
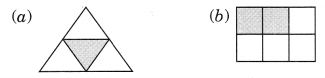
Colour the part according to the fraction given:

Solution:
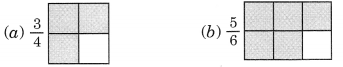
Question 4.
Identify the proper and improper fractions:
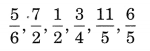
Solution:
Proper fractions are: \(\frac { 5 }{ 6 }\), \(\frac { 1 }{ 2 }\) and \(\frac { 3 }{ 4 }\)
Improper fractions are: \(\frac { 7 }{ 2 }\), \(\frac { 11 }{ 5 }\) and \(\frac { 6 }{ 5 }\)
Question 5.
What fraction of these circles have ‘x’ in them?

Solution:
Fraction of the circles with ‘x’ in the given figure = \(\frac { 5 }{ 8 }\).
Question 6.
Write all the natural numbers from 1 to 15. What fraction of them are prime numbers?
Solution:
Natural numbers from 1 to 15 are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15 Prime numbers from 1 to 15 are 2, 3, 5, 7, 11, 13, i.e., 6 prime numbers.
∴ Fraction of prime numbers = \(\frac { 6 }{ 15 }\)
Question 7.
Identify the like fractions from the following:
![]()
Solution:
\(\frac { 2 }{ 3 }\) and \(\frac { 1 }{ 3 }\) have the same denominator.
∴ \(\frac { 2 }{ 3 }\) and \(\frac { 1 }{ 3 }\) are the like fractions.
Question 8.
Identify the unlike fractions from the following:
![]()
Solution:
\(\frac { 2 }{ 5 }\) , \(\frac { 2 }{ 7 }\) and \(\frac { 1 }{ 6 }\) have different denominators.
∴ \(\frac { 2 }{ 5 }\) , \(\frac { 2 }{ 7 }\) and \(\frac { 1 }{ 6 }\) are unlike fractions.
Question 9.
Convert the following improper fractions into mixed fraction.
![]()
Solution:
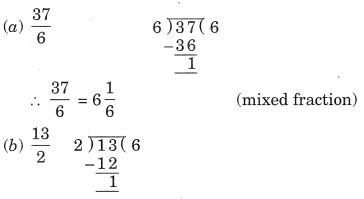
![]()
Question 10.
Convert the following mixed fractions into improper fractions:
![]()
Solution:
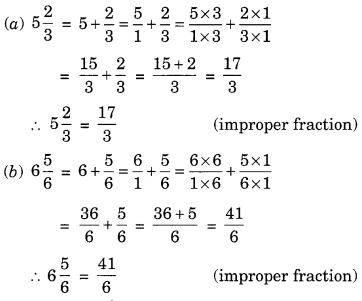
Fractions Class 6 Extra Questions Short Answer Type
Question 11.
Write the following fractions in ascending order:
![]()
Solution:
Here, the numerators of all the fractions are same.
![]()
Question 12.
Write any
(a) three proper and three improper fractions with denominator 7.
(b) two proper and two improper fractions with numerator 9.
Solution:
(a) Proper fractions with denominator 7 are: \(\frac { 2 }{ 7 }\) , \(\frac { 3 }{ 7 }\) and \(\frac { 5 }{ 7 }\)
Improper fractions with denominator 7 are: \(\frac { 9 }{ 7 }\) , \(\frac { 11 }{ 7 }\) and \(\frac { 13 }{ 6 }\)
(b) Proper fractions with numerator 9 are:
\(\frac { 9 }{ 11 }\) and \(\frac { 9 }{ 17 }\)
Improper fractions with numerator 9 are:
\(\frac { 9 }{ 2 }\) and \(\frac { 9 }{ 5 }\)
Question 13.
Compare the following fractions:
![]()
Solution:

Question 14.
![]()
Solution:
LCM of 12, 16 and 24 is 48
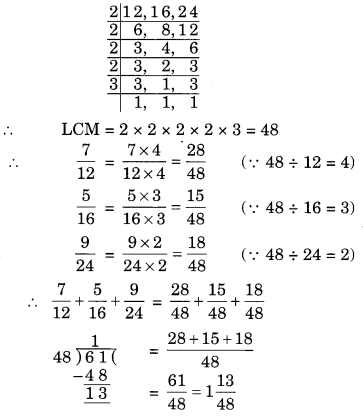
Question 15.
Find the sum of 1\(\frac { 2 }{ 3 }\) and 3\(\frac { 2 }{ 5 }\).
Solution:
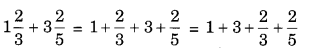
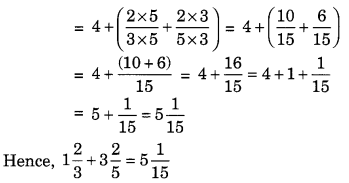
Question 16.
Subtract 2\(\frac { 3 }{ 4 }\) from 4\(\frac { 1 }{ 8 }\).
Solution:
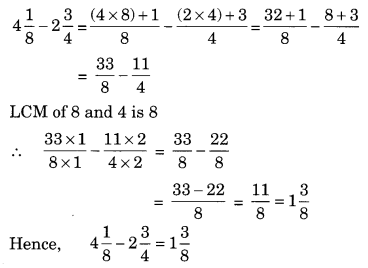
Question 17.
Insert > or < to make each of the following true.
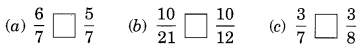
Solution:

Fractions Class 6 Extra Questions Higher Order Thinking Skills (HOTS)
Question 18.
Find the difference between the greatest and the smallest fractions.
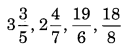
Solution:


Question 19.
Simran painted \(\frac { 2 }{ 3 }\) of the wall space in her room. Her brother Rahul helped and painted \(\frac { 1 }{ 5 }\) of the wall space. How much did they paint together? What part of the whole space is left unpainted?
Solution:
Space of the wall painted by Simran = \(\frac { 2 }{ 3 }\)
Space of the wall painted by Rahul = \(\frac { 1 }{ 5 }\)