Application of Derivatives Class 12 Maths Important Questions Chapter 6

Get access to Class 12 Maths Important Questions Chapter 6 Application of Derivatives, Application of Derivatives Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.

Application of Derivatives Class 12 Important Questions with Solutions Previous Year Questions

Rate Measure, Increasing-Decreasing Functions and Approximation

Question 1.
The total cost C(x) associated with the production of x units of an item is given by C(x) = 0.005x ³ – 0.02x ² + 30x + 5000. Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output. (CBSE 2018)
Answer:
We have, C(x) = 0.005x ³ – 0.02x ² + 30x + 5000
Clearly, the marginal cost, MC (x) = \(\frac{d}{d x}\)C(x)
= \(\frac{d}{d x}\)(0.005x ³ – 0.02x ² + 30x + 500)
= 0.005 × 3x ² – 0.02 × 2x + 30 + 0
= 0.015x ² – 0.04x + 30

Now, marginal cost when 3 units arei produced
MC(3)= 0.015(9) – 0.04(3) + 30
= 0135 – 0.12 + 30= 30.015

Question 2.
The total revenue received from the sale of x units of a product is given by R(x) = 3x ² + 36x + 5 in rupees. Find the marginal revenue when x = 5, where by marginal revenue we mean the rate of change of total revenue with respect to the number of items sold at an instant. (CBSE 2018 C)
Answer:
Marginal Rcvcnuc (MR) = \(\frac{d R}{d x}=\frac{d}{d x}\)(3x ² + 36x + 5)
= 6x + 36
∴ When x = 5
Marginai Revenue (MR) = 6 × 5 + 36 = 66

Question 3.
The volume of a sphere is increasing at the rate of 8 cm ³ /s. Find the rate at which its surface area is increasing when the radius of the sphere is 12 cm. (All India 2017)
Answer:
Let r be the radius, V be the volume and S be the surface area of sphere.

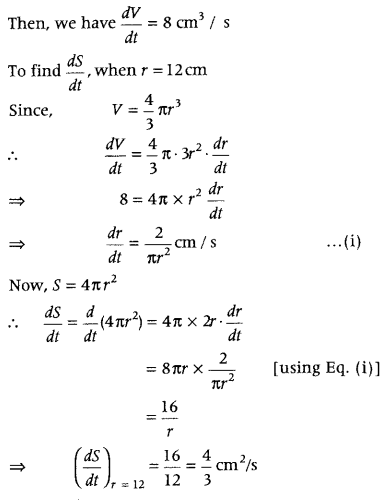
Question 4.
Show that the function f(x) = x ³ – 3x ² + 6x – 100 is increasing on R. (All India 2017)
Answer:
Given, f(x) = x ³ – 3x ² + 6x – 100
On differentiating both sides w.r.t. x, we get
f'(x) = 3x ² – 6x + 6 = 3x ² – 6x + 3 + 3
= 3(x ² – 2x + 1) + 3 = 3(x – 1) ² + 3 > 0
∴ f'(x) > 0
This show that function f(x) is increasing on R.
Hence proved.

Question 5.
The volume of a sphere is increasing at the rate of 3 cubic centimeter per second. Find the rate of increase of its surface area, when the radius is 2 cm. (Delhi 2017)
Answer:
Let r be the radius of sphere and V be its volume. Then,

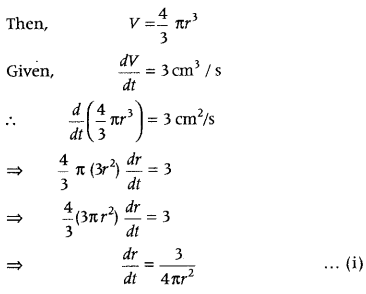
Now, let S be the surface area of sphere, then

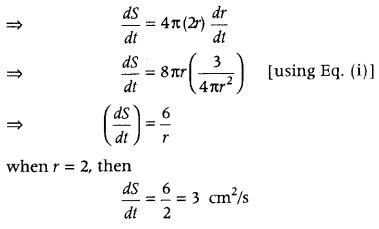
Question 6.
Show that the function f(x) = 4x ³ – 18x ² + 27x – 7 is always increasing on R. (Delhi 2017)
Answer:
We have, f(x) = 4x ³ – 18x ² + 27x – 7
On differentiating both sides w.r.t. x, we get
f(x) = 12x ² – 36x + 27
⇒ f'(x) = 3(4x ² -12x + 9)
⇒ f'(x) = 3(2x – 3) ²
⇒ f(x) > 0
⇒ For any x ∈ R, (2x – 3) ² > 0
Since, a perfect square number cannot be negative.
∴ Given function f(x) is an increasing function on R.

Question 7.
The volume of a cube is increasing at the rate of 8 cm ³ /s. How fast is the surface area increasing when the length of its edge is 12 cm? (All India 2019)
Answer:
Let x be the length of an edge of the cube, V be the volume and S be the surface area at any time t.
Then, V = x ³ and S = 6x ² .

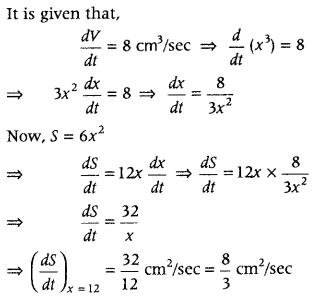
Question 8.
Find the intervals in which the function
f(x) = \(\frac{x^{4}}{4}\) – x ³ – 5x ² + 24x + 12 is
(i) strictly increasing
(ii) strictly decreasing. (CBSE 2018)
Answer:
We have, f(x) = \(\frac{x^{4}}{4}\) – x ³ – 5x ² + 24x + 12
On differentiating both sides w.r.t. x, we get
f(x) = x ³ – 3x ² – 10x + 24
= (x – 2) (x ² – x – 12)
= (x – 2) (x ² – 4x + 3x – 12)
= (x – 2) (x(x – 4) + 3(x – 4)
= (x – 2) (x – 4) (x + 3)
Now, put f'(x) = 0, which gives x = 2, 4 and -3 The points x = -3 x = 2 and x = 4 divides the whole real line into four disjoint intervals namely, (-∞,-3), (-3, 2), (2, 4), (4, ∞)

Note that,
for x ∈ (-∞, – 3), f'(x) < 0 for x ∈ (-3, 2), f(x) > 0
for x ∈ (2, 4), f'(x) < 0 and for x ∈ (4, ∞), f'(x) > 0
∴ f(x) is strictly increasing in the intervals (-3, 2) and (4, ∞), and strictly decreasing in the intervals (-∞, -3) and (2, 4).

Question 9.
Find the intervals in which the function f(x) = -2x ³ – 9x ² – 12x + 1 is
(i) strictly increasing
(ii) strictly decreasing, (CBSE 201B C)
Answer:
Given, f(x) = -2x ³ – 9x ² – 12x + 1
On differentiating both sides w.r.t. x, we get
f'(x) = – 6x ² – 18x – 12
⇒ f'(x) = – 6(x ² + 3x + 2)
⇒ f'(x) = – 6(x ² + 2x + x + 2)
⇒ – 6 [x(x + 2) + 1 (x + 2)]
⇒ – 6 (x + 2) (x + 1)

Now, put f'(x) = 0
⇒ -6(x + 2)(x + 1) = 0
⇒ x = – 2, -1
The points, x = – 2 and x = – 1 divide the real line into their disjoint intervals (-∞,- 2), (- 2, -1) and (- 1, ∞),

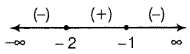
The nature of function in these intervals are given below:

Interval	Sign of f'(x) F’(x) = -6(x + 2)(x + 1)	Nature of function
(-∞, -2)	(-) (-) (-) = (-) < 0	Strictly decreasing
(-2, -1)	(-) (+) (-) = (+) > 0	Strictly increasing
(-1, ∞)	(-) (+) (+) = (-) < 0	Strictly decreasing

Hence, f(x) is strictly increasing in the interval (- 2, -1) and f(x) is strictly decreasing in the interval (- ∞, – 2) ∪ (-1, ∞).

Question 10.
The length x of a rectangle is decreasing at the rate of 5 cm/min and the width y is increasing at the rate of 4 cm/min. When x = 8 cm and y = 6 cm, find the rate of change of
(i) the perimeter.
(ii) area of rectangle. (All India 2017)
Answer:
Using the relation, perimeter of rectangle, P = 2(x + y) and area of rectangle, A = xy, differentiate both sides with respect to t and put them in rate of change value and get the result.
Given that length x of a rectangle is decreasing at the rate of 5 cm/min.
∴ \(\frac{d y}{d x}\) = – 5cm/min ………..(i)
Also, the breadth y of rectangle is increasing at the rate of 4 cm/min.
∴ \(\frac{d y}{d x}\) = 4 cm/min ……(ii)

(i) Here, we have to find rate of change of perimeter, i.e. dP/dt
and we know that, perimeter P = 2 (x + y)

On differentiating both sides w.r.t. t, we get
\(\frac{d P}{d t}\) = 2\(\left(\frac{d x}{d t}+\frac{d y}{d t}\right)\)
⇒ \(\frac{d P}{d t}\) = 2(-5 + 4) = 2(-1) = -2cm/min [from Eqs. (i) and (ii)]
Hence, perimeter of rectangle is decreasing at the rate 2 cm/min.

(ii) Here, we have to find rate of change of area \(\frac{d A}{d t}\)
We know that, area of rectangle A = xy
On differentiating both sides w.r.t. t, we get
\(\frac{d A}{d t}=x \cdot \frac{d y}{d t}+y \cdot \frac{d x}{d t}\)
[by using product rule of derivative]

Now, we have x = 8 cm and y = 6 cm

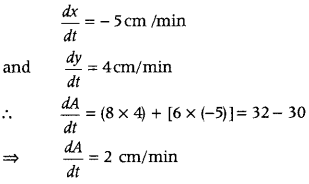
Hence, the area of rectangle is increasing at the rate 2 cm/min.

Question 11.
The side of an equilateral triangle is increasing at the rate of 2 cm/s. At what rate is its area increasing, when the side 22. of the triangle is 20 cm? (Delhi 2015)
Answer:
Let a be the side of an equilateral triangle and A be the area of an equilateral triangle.
Then, \(\frac{d a}{d x}\) = 2 cm/s

We know that, area of an equilateral triangle,
A = \(\frac{\sqrt{3}}{4}\)a ²

On differentiating both sides w.r.t, t, we get

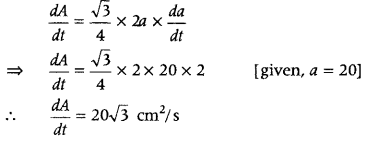
Thus, the rate of area increasing is 20√3 cm ² /s

Question 12.
Find the intervals in which the function f(x) = 3x ⁴ – 4x ³ – 12x ² + 5 is
(i) strictly increasing.
(ii) strictly decreasing. (Delhi 2014)
Answer:
First, find the first derivative and put equal to zero, we get different values of x and then divide the real line into disjoint intervals. Further check sign of f(x) in a given interval, if f'(x) > 0, then it is strictly increasing and if f'(x) < 0, then it is strictly decreasing.
f(x) = 3x ⁴ – 4x ³ – 12x ² + 5
On differentiating both sides w.r.t. x, we get
f'(x) = 12x ³ -12x ² – 24x
For strictly increasing or strictly decreasing, put f'(x) = 0, we get
12x ³ – 12x ² – 24x = 0
⇒ 12x [x ² – 2x + x – 2] = 0
12x (x + 1) (x – 2) = 0
∴ x = 0, -1 or 2
Now, we find intervals in which f(x) is strictly increasing or strictly decreasing.

Interval	f’(x) = 12x(x + 1)(x – 2)	Sign of f’(x)
x < – 1	(-) (-) (-)	– ve
– 1 < x < 0	(-) (+) (-)	+ ve
0 < x < 2	(+) (+) (-)	– ve
x > 2	(+) (+) (+)	+ ve

We know that, a function f(x) is said to be strictly increasing , if f'(x) > 0 and it is said to be strictly decreasing , if f'(x) < 0. So, the given function f(x) is
(i) strictly increasing on the intervals (-1, 0) and (2, ∞).
(ii) strictly decreasing on the intervals (-∞, -1) and (0, 2).

Question 13.
Find the intervals in which the function given by ;
f(x) = \(\frac{3}{10}\) x ⁴ – \(\frac{4}{5}\)x ³ – 3x ² + \(\frac{36x}{5}\) + 11 is
(i) strictly increasing.
(ii) strictly decreasing. (All India 2014C)
Answer:
(i) Strictly increasing in (-2, 1) and (3, ∞).
(ii) Strictly decreasing in (-∞,- 2) and (1, 3).

Question 14.
The sides of an equilateral triangle are increasing at the rate of 2 cm/s. Find the rate at which the area increases, when the side is 10 cm? (All India 2014C)
Answer:
10√ 3 cm ² /s

Question 15.
Find the value(s) of x for which y = [x(x – 2)] ² is an increasing function. (All India 2014; Delhi 2010)
Answer:
Given function is y = [x(x – 2)] ² = [x ² – 2x] ² .
On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = 2(x ² – 2x) – (x ² – 2x)
= 2(x ² – 2x) (2x – 2) = 4x(x – 2) (x -1)

On putting \(\frac{d y}{d x}\) = 0, we get
4x(x – 2)(x – 1) = 0 ⇒ x = 0, 1 and 2

Now, we find interval in which f(x) is strictly increasing or strictly decreasing.

Interval	\(\frac{d y}{d x}\) = 4x(x – 2)(x – 1)	Sign of f’(x)
(-∞, 0)	(-) (-) (-)	– ve
(0, 1)	(-) (+) (-)	+ ve
(1, 2)	(+) (+) (-)	– ve
(2, ∞)	(+) (+) (+)	+ ve

Hence, y is strictly increasing in (0, 1) and (2, ∞). Also, y is a polynomial function, so it continuous at x = 0, 1 and 2. Hence, y is increasing in [0, 1] ∪ [2, ∞).

Question 16.
Using differentials, find the approximate value of (3.968) ^3/2 . (Delhi 2014C)
Answer:
Let y = f(x) = (x) ^3/2
On differentiating both sides w.r.t. x, we get
Let x = 4 and x + Δx = 3.968
Then, Δx = -0.032
Now, f(x+ Δx) ^3/2 ≈ f(x) + f'(x)Δx
(x+ Δx) ^3/2 ≈ (x) ^3/2 + \(\frac{3}{2}\).(x) ^1/2 .(-0.032)
⇒ (4 – 0.032) ^3/2 ≈ (4) ^3/2 + \(\frac{3}{2}\)(4) ^1/2 (-0.032) [put x = 4]
⇒ (3.968) ^3/2 ≈ 8 + \(\frac{3}{2}\) .2.(-0.032)
⇒ (39368) ^3/2 ≈ 8 – 0.096
⇒ (3.968) ^3/2 ≈ 7.904

Question 17.
Find the intervals in which the function
f(x) = \(\frac{3}{2}\) x ⁴ – 4x ³ – 45x ² + 51 is
(i) strictly increasing.
(ii) strictly decreasing. (Foreign 2014C)
Answer:
(i) Strictly increasing in (-3, 0) and (5, ∞).
(ii) Strictly decreasing in (-∞,- 3) and (0,5).

Question 18.
Find the approximate value of f(3.02), upto 2 places of decimal, where
f(x) = 3x ² + 15x + 3. (Foreign 2014)
Answer:
First, split 3.02 into two parts x and Ax, so that x + Δx = 3.02 and f(x + Δx) = f(3.02)
Now, write f(x + Δx) = f(x) + Δx . f'(x) and use this result to find the required value.
Given function is f(x) = 3x ² + 15x + 3
On differentiating both sides w.r.t. x, we get f'(x) = 6x + 15
Let x = 3 and Δx = 0.02
So that f(x + Δx) – f(302)
By using f(x + Δx) ~ f(x)+ Δx f'(x), we get
f(x + Δx) = 3x ² + 15x + 3 + (6x + 15) Δx
f(3 + 0.02) = 3(3) ² + 15(3) + 3+ [6(3) + 15] (0.02)
= 27 + 45 + 3 + 33(0.02)
= 75 + 0.66
= 75.66
Hence, f (3.02) ≈ 75.66

Question 19.
Using differentials, find approximate value of \(\sqrt{49.5}\). (Delhi2012)
Answer:
First, divide 49.5 into two parts as x = 49 and ∆x = 0.5. Now, let y = √x and find \(\frac{d y}{d x}\). Finally, find Δy using the formula dy = \(\frac{d y}{d x}\).Δx
Let x = 49, ∆x = 0.5 and y = √x
On differentiating both sides w.r.t. x, we get

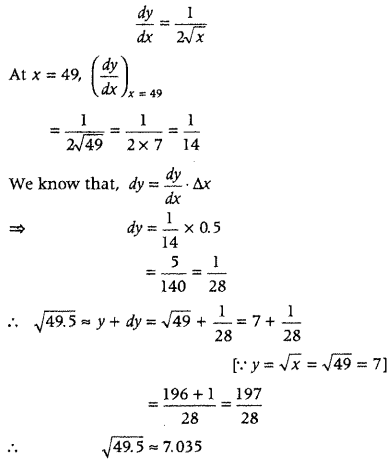
Hence, approximate value of \(\sqrt{49.5}\) is 7.035

Question 20.
A ladder 5 m long is leaning against a wall. Bottom of ladder is pulled along the ground away from wall at the rate of 2 m/s. How fast is the height on the wall decreasing, when the foot of ladder is 4 m away from the wall? (All India 2012)
Answer:
First, draw a rough figure of a right angled triangle, then use Pythagoras theorem. Further differentiate the relation between sides with respect tof and ; simplify it
Let AC be the ladder, BC = x and height of the wall, AB = y.

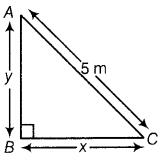
As the ladder is pulled along the ground away
from the wall at the rate of 2 m/s.
So, \(\frac{d y}{d x}\) = 2m/s
To find ,when x = 4.
In right angled MBC, by Pythagoras theorem, we get
(4) ² + (BC) ² =(AC) ²
x ² + y ² = 25
(4) ² + y ² = 25
16 + y ² = 25
y ² = 9
y = √9 [taking positive square root]
∴ y = 3
On differentiating both sides of Eq. (i) w.r.t. t, we get

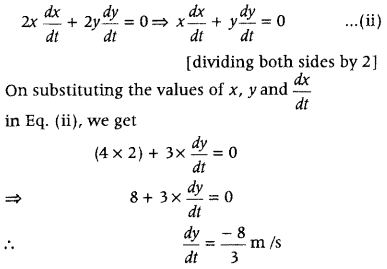
Hence, height of the wall is decreasing at the rate of \(\frac{8}{3}\)m/s.
Note: In a rate of change of a quantity, +ve sign shows that it is increasing and – ve sign shows that it is decreasing.

Question 21.
Show that y = log(1 + x) – \(\frac{2 x}{2+x}\), x > – 1 is an increasing function of x, throughout its domain. (Foreign 2012)
Answer:
Given Function is y = log(1 + x) – \(\frac{2 x}{2+x}\)
On differentiating both sides w.r.t. x, we get

Now, x ² , (2 + x) ² are always positive, also 1 + x > 0 for x > -1
From Eq. (i), \(\frac{d y}{d x}\) > 0 for x > – 1
Hence, function increases for x > -1.

Question 22.
Find the intervals in which the function given by f(x) = sin x + cos x, 0 ≤ x ≤ 2π is
(i) increasing
(ii)decreasing. (Delhi 2012c)
Answer:
Given function is f(x) = sin x + cos x.
On differentiating both sides w.r.t. x, we get
f'(x) = cos x – sin x
Now, put f'(x) = 0 ⇒ cos x – sinx = 0
⇒ tan x = 1 ⇒ x = \(\frac{\pi}{4}, \frac{5 \pi}{4}\), as 0 ≤ x ≤ 2π
Now, we find the intervals in which f(x) is strictly increasing or strictly decreasing

Note that, f'(x) > 0 in (0, \(\frac{\pi}{4}\)), f'(x) < 0 in, \(\left(\frac{\pi}{4}, \frac{5 \pi}{4}\right)\) and f'(x) > 0 in (\(\frac{5 \pi}{4}\), 2π).
Since, f(x) is a trigonometric function, so it is
continuous at x = 0, \(\frac{\pi}{4}, \frac{5 \pi}{4}\) and 2π.

Hence, the function is
(i) increasing in [0, \(\frac{\pi}{4}\)] and [\(\frac{5\pi}{4}\), 2π]
(ii) decreasing in \(\left[\frac{\pi}{4}, \frac{5 \pi}{4}\right]\)

Question 23.
Find the intervals in which the function given by f(x) = x ⁴ – 8x ³ + 22x ² – 24x + 21 is
(i) increasing,
(ii) decreasing. (All Delhi 2012C)
Answer:
Given function is
f(x) = x ⁴ – 8x ³ + 22x ² – 24x + 21
On differentiating both sides w.r.t. x, we get
f(x) = 4x ³ – 24x ² + 44x – 24
= 4(x ³ – 6x ² + 11 x – 6)
= 4(x – 1) (x ² – 5x + 6)
= 4(x – 1) (x – 2) (x – 3)
Put f'(x) = 0
⇒ 4(x – 1)(x – 2)(x – 3) = 0
⇒ x = 1, 2, 3
So, the possible intervals are (-∞, 1), (1, 2), (2, 3) and (3, ∞).
For interval (- ∞, 1), f'(x) < 0 For interval (1, 2), f'(x) > 0
For interval (2, 3), f'(x) < 0 For interval (3, ∞), f'(x) > 0.

Also, as f(x) is a polynomial function, so it is continuous at x = 1, 2, 3…………. Hence,
(i) function increases in [1, 2] and [3, ∞).
(ii) function decreases in (-∞, 1 ] and [2, 3]

Question 24.
Sand is pouring from the pipe at the rate of 12 cm3/s. The falling sand forms a cone on a ground in such a way that the height of cone is always one-sixth of radius of the base. How fast is the height of sand 5 cone increasing when the height is 4 cm? (Delhi 2011)
Answer:
Let V be the volume of cone, h be the height and r be the radius of base of the cone.
Given, \(\frac{d V}{d t}\) = 12 cm ³ /s ……(i)

Also, height of cone = \(\frac{1}{6}\) × (radius of base of cone)
∴ h = \(\frac{1}{6}\)r or r = 6h ………..(ii)

We know that, volume of cone is given by
V = \(\frac{1}{3}\)πr ² h …(iii)

On putting r = 6h from Eq. (ii) in Eq. (iii), we get

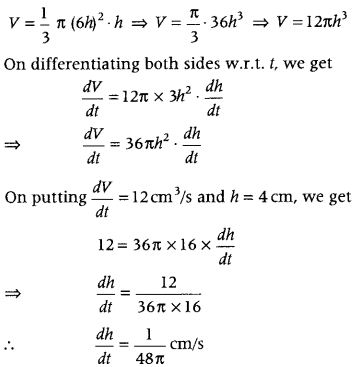
Hence, the height of sand cone is increasing at the rate of 1/48π cm/s.

Question 25.
If the radius of sphere is measured as t 9 cm with an error of 0.03 cm, then find the approximate error in calculating its surface area. (All India 2011)
Answer:
Let S be the surface area, r be the radius of the sphere.
Given, r = 9 cm
Then, dr = Approximate error in radius r = 0.03 cm
and dS = Approximate error in surface area
Now, we know that surface area of sphere is given by
S = 4πr ²
On differentiating both sides w.r.t. r, we get
\(\frac{d S}{d r}\) = 4π × 2r = 8πr
dS = 8πr × dr
⇒ dS = 8π × 9 × 0.03 [∵ r = 9 cm and dr = 0.03 cm ]
⇒ dS = 72 × 0.03π
∴ dS = 2.16π cm ² /cm
Hence, approximate error in surface area is 2.16π cm ² /cm.

Question 26.
Find the intervals in which the function
f(x) = sin x + cos x, 0 ≤ x ≤ 2π is strictly l increasing and strictly decreasing. (Foreign 2011)
Answer:
Strictly increasing in the intervals [0, \(\frac{\pi}{4}\)) and (\(\frac{5 \pi}{4}\), 2] strictly decreasing in the intervals \(\left(\frac{\pi}{4}, \frac{5 \pi}{4}\right)\)

Question 27.
Show that the function f(x) = x ³ – 3x ² + 3x, x ∈ R is increasing on R. (All India 2011C)
Answer:
We know that, a continuous function y = f(x) is said to be increasing on R, if \(\frac{d y}{d x}\) ≥ 0, ∀ x ∈ R.
Given, y = x ³ – 3x ² + 3x

On differentiating both sides w.r.t. x, we get

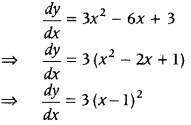
Now, 3(x – 1) ² ≥ 0 for all real values of x, i.e. ∀ x ∈ R.
Hence, the given function is increasing on R.

Question 28.
Find the intervals in which the function
f(x) = (x – 1 ) ³ (x – 2) ² is
(i) increasing,
(ii) decreasing. (All India 2011C)
Answer:
Given, f(x) = (x – 1 ) ³ (x – 2) ²

On differentiating both sides w.r.t. x, we get
f'(x) = (x – 1) ³ .\(\frac{d}{d x}\)(x – 2) ² + (x – 2) ² .\(\frac{d}{d x}\)(x – 1) ³
⇒ f'(x) = (x – 1) ³ – 2(x – 2)+ (x – 2) ² 3(x – 1) ²
= (x – 1) ² (x – 2)[2(x – 1) + 3(x – 2)]
= (x – 1) ² (x – 2) (2x – 2 + 3x – 6)
⇒ f’(x) = (x – 1) ² (x – 2){3x – 8)

Now, put f'(x) = 0
⇒ (x – 1) ² (x – 2) (5x – 8) = 0
Either (x – 1) ² = 0 or x – 2 = 0 or 5x – 8 = 0
∴ x = 1, \(\frac{8}{5}\), 2
Now, we find intervals and check in which interval f(x) is strictly increasing and strictly decreasing.

Interval	f’(x) = (x – 1) 2 (x – 2)(5x – 8)	Sign of f’(x)
x < 1	(+) (-) (-)	+ve
1 < x < \(\frac{8}{5}\)	(+) (-) (-)	+ ve
\(\frac{8}{5}\) < x < 2	(+) (-) (+)	– ve
x > 2	(+) (+) (+)	+ ve

We know that, a function f(x) is said to be an strictly increasing function, if f'(x) > 0 and strictly decreasing, if f'(x) < 0. So, the given function f(x) is increasing on the intervals (-∞, 1) (1, \(\frac{8}{5}\)) and (2, ∞) and decreasing on continuous at x = 1, -, 2 Hence, f(x) is
(i) increasing on intervals I
(ii) decreasing on interval
Note: Every strictly increasing (strictly decreasing) function is incresing (decreasing) but converse need not be true.

Question 29.
Find the intervals in which the function
f(x) = 2x ³ + 9x ² + 12x + 20 is
(i) increasing
(ii) decreasing. (Delhi 2011c)
Answer:
Given function is f(x) = 2x ³ + 9x ² + 12x + 20
On differentiating both sides w.r.t. x, we get f(x) = 6x ² + 18x + 12
Put f'(x) = 0, we get
6x ² + 18x + 12 = 0
⇒ 6(x ² + 3x + 2) = 0
⇒ 6 (x + 1) (x + 2) = 0
⇒ (x + 1) (x + 2) = 0
⇒ x + 1= 0 or x + 2 = 0
x = – 2, -1
Now, we find intervals and check in which interval f(x) is strictly increasing and strictly decreasing.

Interval	f’(x) = 6(x + 1)(x + 2)	Sign of f’(x)
x < -2	(+) (-) (-)	+ ve
-2 < x < -1	(+) (-) (+)	– ve
x > -1	(+) (+) (+)	+ ve

We know that, a function f(x) is said to be an strictly increasing function, if f'(x) > 0 and strictly decreasing, if f'(x) < 0. So, given function is increasing on intervals (-∞,- 2) and (-1, ∞) and decreasing on interval (-2, -1).
Since, f(x) is a polynomial function, so it is continuous at x = -1, – 2.
Hence, given function is
(i) increasing on intervals (-∞, – 2] and [-1, ∞).
(ii) decreasing on interval [-2,-1 ].

Question 30.
Find the intervals in which the function
f(x) = 2x ³ – 9x ² + 12x -15 is
(i) increasing.
(ii) decreasing. (Delhi 2011c)
Answer:
(i) The function increasing on intervals (- ∞, 1]and [2, ∞).
(ii) The function decreasing on interval [1, 2]

Question 31.
Find the intervals in which the function
f(x) = 2x ³ – 15x ² + 36x + 17 is increasing or decreasing. (All India 2010c)
Answer:
The function increasing on (- ∞, 2] and [3, ∞) and decreasing on [2, 3]

Question 32.
Find the intervals in which the function
f(x) = 2x ³ – 9x ² + 12x + 15 is
(i) increasing.
(ii) decreasing. (All India 2010C)
Answer:
(i) The function increasing on (- ∞,1] and [2, ∞).
(ii) The function decreasing on [1, 2]

Question 33.
Prove that y = \(\frac{4 \sin \theta}{2+\cos \theta}\) – θ is an increasing function in (0, \(\frac{\pi}{2}\)). (All India 2016, 2011)
Answer:
To prove that given function is increasing, prove that \(\frac{d y}{d \theta}\) ≥ 0 for all θ.
Given function is y = \(\frac{4 \sin \theta}{2+\cos \theta}\) – θ
We know that, a function y = f(x) is said to be an increasing function, if \(\frac{d y}{d \theta}\) ≥ 0, for all values of x.
On differentiating both sides of Eq. (i) w.r.t. θ, we get

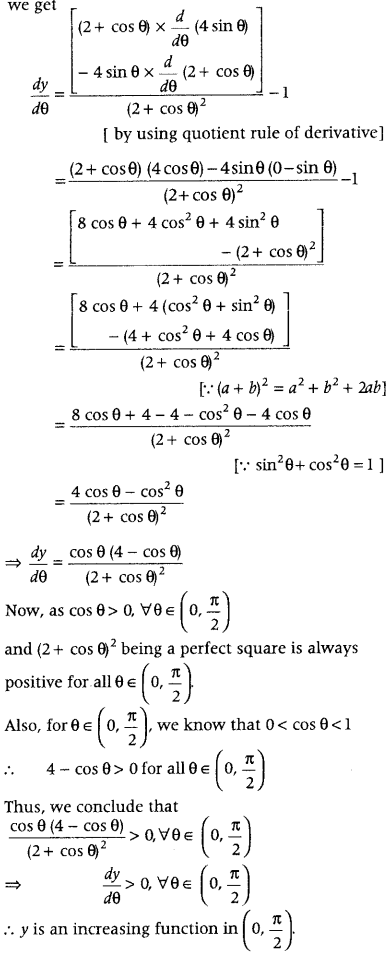
Hence Proved.

Question 34.
Find the intervals in which the function f(x) = sin 3x – cos 3x, 0 < x < π, is strictly increasing or strictly decreasing. (Delhi 2016)
Answer:
Given, f(x) = sin 3x – cos 3x, 0 < x < π
On differentiating both sides w.r.t. x, we get
f'(x) = 3cos 3x + 3sin 3x

On putting f'(x) = 0, we get
sin 3x = -cos 3x ⇒ tan 3x = – 1
⇒ 3x = \(\frac{3 \pi}{4}, \frac{7 \pi}{4}, \frac{11 \pi}{4}\) [∵ tan θ is negative in IInd and IVth quadrants]
⇒ x = \(\frac{\pi}{4}, \frac{7 \pi}{12}, \frac{11 \pi}{12}\)
Now, we find intervals and check in which intervals f(x) is strictly increasing or strictly decreasing.

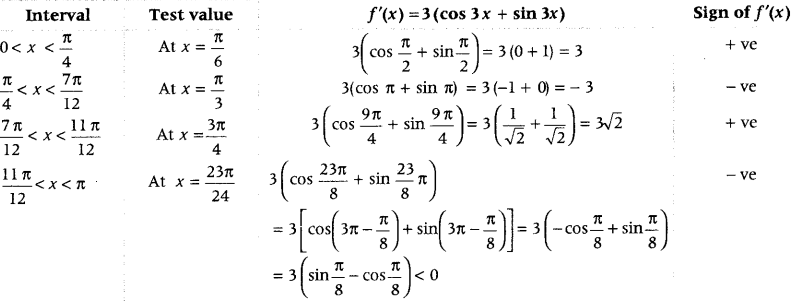
Here, we see that f(x) > 0, for 0 < x < \(\frac{\pi}{4}\) and \(\frac{7\pi}{12}\) < x < \(\frac{11 \pi}{12}\) so f(x) is strictly increasing in the intervals (0, \(\frac{\pi}{4}\)) and \(\left(\frac{7 \pi}{12}, \frac{11 \pi}{12}\right)\)

While f'(x) < 0 in \(\frac{\pi}{4}\) < x < \(\frac{7\pi}{12}\) and \(\frac{11 \pi}{12}\) < x < π
So, f(x) is strictly decreasing in the intervals \(\left(\frac{\pi}{4}, \frac{7 \pi}{12}\right)\) and (\(\frac{11 \pi}{12}\), π)

Question 35.
Prove that the function f defined by f(x) = x ² – x + 1 is neither increasing nor decreasing in (-1, 1). Hence, find the intervals in which f(x) is
(i) strictly increasing.
(ii) strictly decreasing. (Delhi 2014C)
Answer:
Given function is f(x) = x ² – x + 1.
On differentiating both sides w.r.t. x, we get f'(x) = 2x – 1
On putting f'(x) = 0 ⇒ 2x – 1 = 0 ⇒ x = \(\frac{1}{2}\)

Now, we find intervals in which f(x) is strictly increasing or strictly decreasing.

Interval	f'(x) = (2x – 1)	Sign of f'(x)
x < \(\frac{1}{2}\)	(-)	-ve
x > \(\frac{1}{2}\)	(+)	+ve

Here, f(x) is strictly increasing on (\(\frac{1}{2}\), ∞) and f(x) is strictly decreasing on (- ∞, \(\frac{1}{2}\))
⇒ f(x) is strictly increasing on (\(\frac{1}{2}\), 1) and f(x) is strictly decreasing on (-1, \(\frac{1}{2}\))
∴ f'(x) does not have same sign throughout the interval (-1, 1).
Thus, f(x) is neither increasing nor decreasing in (-1, 1).

Question 36.
Find the intervals in which the function
f(x) = 20 – 9x + 6x ² – x ³ is
(i) strictly increasing.
(ii) strictly decreasing. (All India 2010)
Answer:
Given function is f(x) = 20 – 9x + 6x ² – x ³ .
On differentiating both sides w.r.t. x, we get f'(x) = – 9 + 12x – 3x ²
On putting f'(x) = 0, we get
-9 + 12x – 3x ² = 0
⇒ -3(x ² – 4x + 3) = 0
⇒ -3(x – 1)(x – 3) = 0
⇒ (x – 1)(x – 3) = 0
⇒ x – 1 = 0 or x – 3 = 0 ⇒ x = 1 or 3
Now, we find intervals in which f(x) is strictly increasing or strictly decreasing.

Interval	F(x) = – 3 (x -1) (x – 3)	Sign of f'(x)
x < 1	(-) (-) (-)	– ve
1< x < 3	(-) (+) (-)	+ ve
x > 3	(-) (+) (+)	– ve

We know that, a function f(x) is said to be strictly increasing when f'(x) > 0 and it is said to be strictly decreasing, if f'(x) < 0. So, the given function f(x) is (i) strictly increasing on the interval (1, 3) and (ii) strictly decreasing on the intervals (-∞, 1) and (3, ∞).

Question 37.
Find the intervals in which the function given by f(x) = sinx – cosx, 0 ≤ x ≤ 2π is strictly increasing or strictly decreasing. (Delhi 2010)
Answer:
Given function is f(x) = sin x – cos x, 0 ≤ x ≤ 2π
On differentiating both sides w.r.t. x, we get f'(x) = cos x + sin x
On putting f'(x) = 0, we get

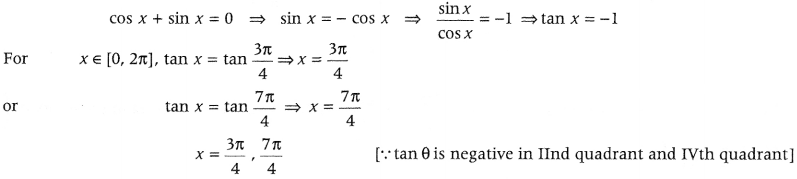
Now, we find the intervals in which f(x) is strictly increasing or strictly decreasing.

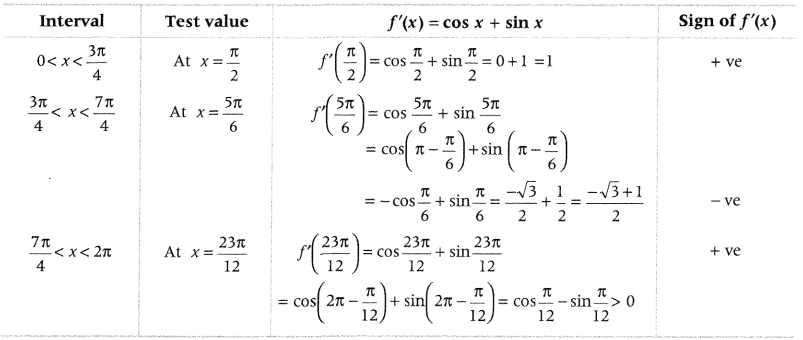
We know that, a function f(x) is said to be strictly increasing in an interval when f’(x) > 0 and it is said to be strictly decreasing when f’(x) < 0.
So, the given function f(x) is strictly increasing in intervals (o, \(\frac{3 \pi}{4}\)) and (\(\frac{7 \pi}{4}\), and it is strictly decreasing in the interval \(\left(\frac{3 \pi}{4}, \frac{7 \pi}{4}\right)\)

Tangents and Normals

Question 1.
Find the equation of tangent to the curve y = \(\sqrt{3 x-2}\) which is parallel to the line 4x – 2y + 5 = 0. Also, write the equation of normal to the curve at the point of contact. (Delhi 2019)
Answer:
Let (x ₁ , y ₁ ) be the point on curve from which tangent to be taken. We know that, slope of tangent is given by

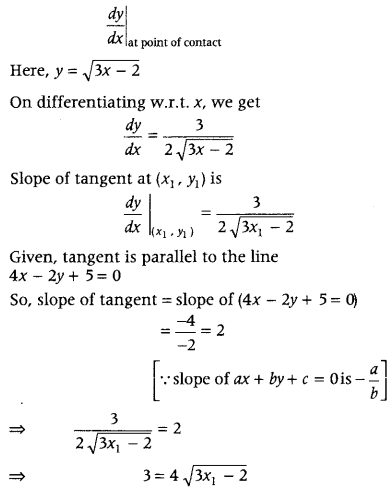
On squaring both sides, we get
9 = 16(3x ₁ – 2)
⇒ 3x ₁ = \(\frac{9}{16}\) + 2 ⇒ x ₁ = \(\frac{41}{48}\)

Since, point (x ₁ , y ₁ ) is on the curv, therefore y ₁ = \(\sqrt{3 x_{1}-2}\)
⇒ y ₁ = \(\sqrt{3 \times \frac{41}{48}-2}=\frac{3}{4}\)
Hence, the point is (x ₁ , y ₁ )

Now, equation of the tangent is given by
y – y ₁ = m(x – x ₁ )
⇒ y – \(\frac{3}{4}\) = 2(x – \(\frac{41}{48}\))
⇒ \(\frac{4 y-3}{4}=\frac{48 x-41}{24}\)
⇒ \(\frac{24}{4}\)(4y – 3) = 48x – 41
⇒ 6(4y – 3) = 48x – 41
⇒ 48x – 41 – 24y + 18 = 0
⇒ 48x – 24y = 23,
which is the required equation of the tangent.

Now, equation of the normal is given by

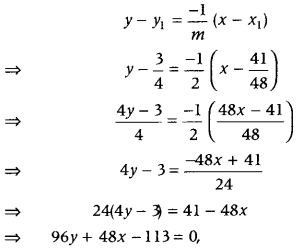
which is the required equation of the normal.

Question 2.
Find the equation of the normal to the curve x ² = 4y, which passes through the point (-1, 4). (All India 2019)
Answer:
Given curve is x ² = 4y

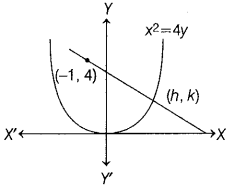
On differentiating w.r.t. x, we get
2x = 4\(\frac{d y}{d x}\)
⇒ \(\frac{d y}{d x}=\frac{2 x}{4}=\frac{x}{2}\)

Slope of normal = \(-\frac{1}{\frac{d y}{d x}}=-\frac{1}{\frac{x}{2}}=-\frac{2}{x}\)
Let (h, k) be the point where normal and curve intersect.

Then, slope of normal at (h, k) = – \(\frac{2}{h}\)
Equation of normal passing through (h, k) with slope – \(\frac{2}{h}\) is h
y – k = – \(\frac{2}{h}\) (x – h)
Since normal passes through (-1, 4). It will satisfy its equation

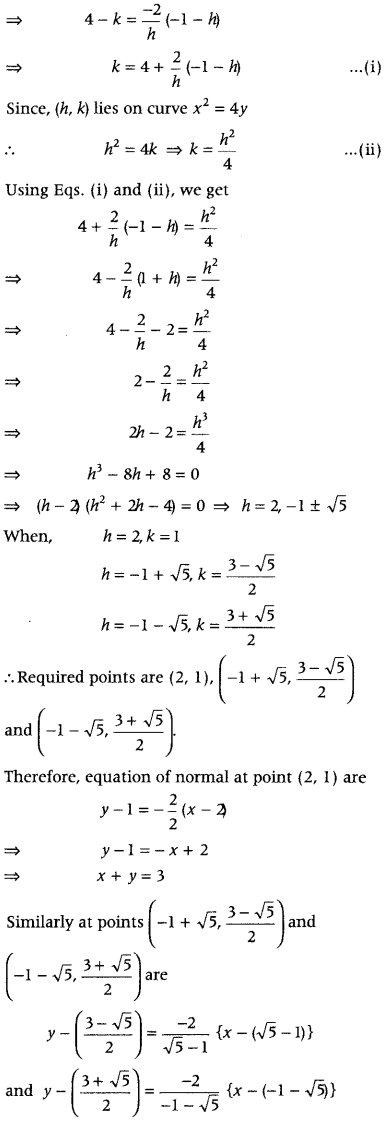
Question 3.
Find the equations of the tangent and the normal to the curve 16x ² + 9y ² = 145 at the point (x ₁ , y ₁ ), where x ₁ = 2 and y ₁ > 0. (CBSE 2018)
Answer:
Given equation of curve is 16x ² + 9y ² = 145
Clearly, when x = 2, then
16(2) ² + 9y ² =145
9y ² = 145 – 64
⇒ 9y ² = 81
⇒ y ² = 9
⇒ y = ±3
[taking square root on both sides]
But it is given that y ₁ > 0
y = 3

Thus, the point of contact (x ₁ , y ₁ ) = (2, 3)
Now, on differentiating both sides of Eq. (i) w.r.t. x, we get

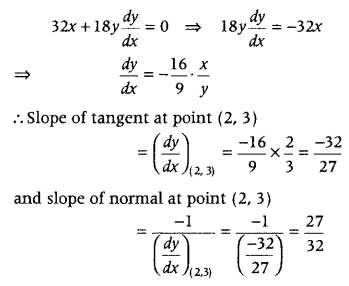
Now, equation of tangent at point (2, 3) is
(y – 3) = \(\frac{-32}{27}\)(x – 2)
⇒ 27y – 81 = -32x + 64 ⇒ 32x + 27y = 145
and equation of normal at point (2, 3 )is
(y – 3) = \(\frac{27}{32}\)(x – 2)
⇒ 32y – 96 = 27x – 54
⇒ 27x – 32y = -42

Question 4.
Find the angle of intersection of the curves x ² + y ² = 4 and (x – 2) ² + y ² = 4, at the point in the first quadrant. (CBSE 2018C)
Answer:
Given curves are x ² + y ² = 4 and (x – 2) ² + y ² = 4
From Eqs. (i) and (ii), we get
x ² + 4 – 4x + y ² = 4
⇒ 4 – 4x = 0 ⇒ x = 1

On putting value of x in Eq. (i), we get
y = √3
[since point taken in first quadrant]
∴ Point of intersection is (1, √3).
On differentiating both sides of Eq. (i), we get

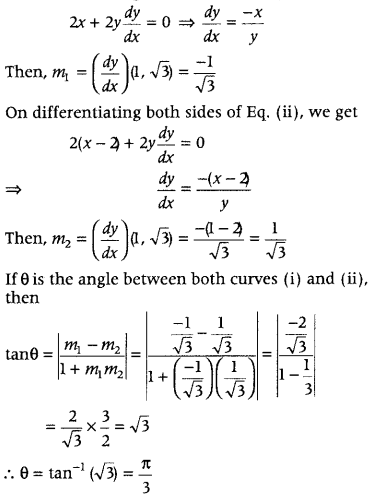
∴ Angle of intersection between the curves is \(\frac{\pi}{3}\).

Question 5.
Show that the equation of normal at any point t on the curves x = 3 cos t – cos ³ t and y = 3 sin t – sin ³ t is 4 (y cos ³ t – x sin ³ t) = 3 sin 4t. (Delhi 2016)
Answer:
Given equations of curves are
x = 3cost – cos ³ t and
y = 3sint – sin ³ t
On differentiating w.r.t. t, we get

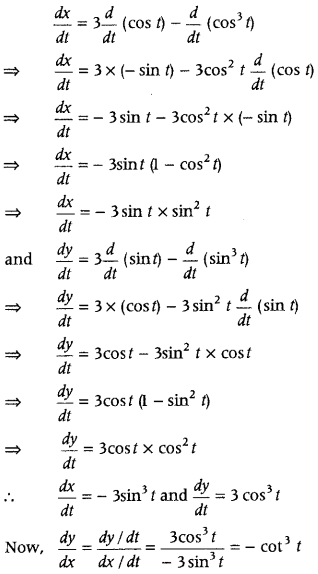
∴ Equation of normal is
y – (3 sin t – sin ³ t) = –\(-\frac{1}{-\cot ^{3} t}\) [x – (3cos t – cos ³ t)] [∵ y – y ₁ = –\(-\frac{1}{d y / d x}\)(x – x ₁ )
⇒ (y – 3sinf + sin ³ t) = (x – 3cos t + cos ³ t)
⇒ ycos ³ t – 3sin t cos ³ t + sin ³ t cos ³ t
⇒ xsin ³ t – 3sin ³ t cos t + sin ³ t cos ³ t
⇒ y cos ³ t – xsin ³ t = 3sin t cos ³ t – 3sin ³ t cost
⇒ y cos ³ t – xsin ³ t = 3sint cos t(cos ² t – sin ² t)
= 3sint cost(cos2t) × \(\frac{2}{2}\) [∵ cos ² t – sin ² t = cos 2t]
= \(\frac{3}{2}\)sin 2t × cos 2t [∵ 2sin t cos t = sin 2t]
= \(\frac{3}{2}\)sin 2t × cos 2t × \(\frac{2}{2}\)
= \(\frac{3}{2}\)sin 4t [∵ 2sin 2t cos 2t = sin 4t]
∴ 4(y cos ³ t – x sin ³ t) = 3 sin 4t
Hence Proved.

Question 6.
Find the equation of tangents to the curve y = x ³ + 2x – 4 which are perpendicular to the line x + 14y – 3 = 0. (All India 2016)
Answer:
Given equation of curve is
y = x ³ + 2x – 4

On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = 3x ² + 2

∴ The slope of required tangent is
m ₁ = \(\frac{d y}{d x}\) = 3x ² + 2

Now, slope of line x + 14y – 3 = 0
or y = \(-\frac{x}{14}+\frac{3}{14}\)
is m ₂ = \(-\frac{1}{14}\)

Since, the required tangent is perpendicular to the line x + 14y -3=0.
∴ m ₁ m ₂ = -1
⇒ (3x ² + 2) × \(\left(-\frac{1}{14}\right)\) = -1
⇒ 3x ² + 2 = 14
⇒ 3x ² = 12 ⇒ x ² = 4
⇒ x =± 2

When x = 2, then
y = 2 ³ + 2 × 2- 4= 8 + 4 – 4 = 8

When x = – 2, then
y = (-2) ³ + 2 × (-2) – 4
= -8 – 4 – 4 = -16
∴ Points of contact are (2, 8) and (- 2, -16).

Now, equation of tangent at point (2, 8) is
⇒ y – 8 = \(\left(\frac{d y}{d x}\right)_{(2,8)}\) (x – 2)
⇒ y – 8 = ( 3 × 2 ² + 2)(x – 2)
⇒ y – 8 = 14(x – 2)
⇒ y = 14x – 20

and equation of tangent at point (- 2, -16) is
⇒ y + 16 = \(\frac{d y}{d x}_{(-2,-16)}\) (x + 2)
⇒ y + 16 = [3 (- 2) ² + 2](x + 2)
⇒ y + 16 = 14 (x + 2)
⇒ y = 14x + 12
Hence, the required equation of tangents are y = 14x – 20 and y = 14x + 12

Question 7.
The equation of tangent at (2, 3) on the curve y ² = ax ³ + b is y = 4x – 5. Find the values of a and b. (All India 2016)
Answer:
Given equation of curve is y ² = ax ³ + b . and equation of tangent is y = 4x – 5
On differentiating both sides of Eq. (i) w.r.t. x, we get

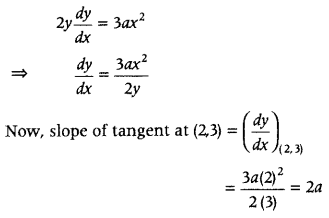
But, from Bq. (ii), we have slope of tangent = 4
∴ 2a = 4 ⇒ a = 2 (1)
Since, (2, 3) lies on the curve, therefore from Eq. (i), we get
9 = 8a+b (1)
⇒ 9 = 16+ b
⇒ b = – 7 [∵ a = 2]
Hence, a = 2 and b = -7

Question 8.
Find the point on the curve 9y ² = x ³ , where the normal to the curve makes equal intercepts on the axes. (Foreign 2015)
Answer:
Given curve is 9y ² = x ³ …(i)
On differentiating both sides w.r.t. x, we get
9 × 2y\(\frac{d y}{d x}\) = 3x ² ⇒ \(\frac{d y}{d x}=\frac{3 x^{2}}{18 y}=\frac{x^{2}}{6 y}\)
Let (x ₁ , y ₁ ) be the required point on the curve (i).

Then, slope of normal to the curve (i) at point (x ₁ , y ₁ )

Hence, required points are (4, \(\frac{8}{3}\)) and (4, \(\frac{-8}{3}\))
Note that x ₁ ≠ 0, as x ₁ = 0, then y ₁ = 0. So, normal will pass through (0, 0), which is not possible.

Question 9.
Find the equations of the tangent and normal to the curves x = a sin ³ θ and y = a cos ³ θ at θ = \(\frac{\pi}{4}\). (Delhi 2014)
Answer:
Given, x = a sin ³ θ
On differentiating both sides w.r.t. θ, we get
\(\frac{d x}{d \theta}\) = a(3sin ² θ cos θ)
⇒ \(\frac{d x}{d \theta}\) = 3a sin ² θ cos θ
and y = a cos ³ θ

On differentiating both sides w.r.t. θ, we get

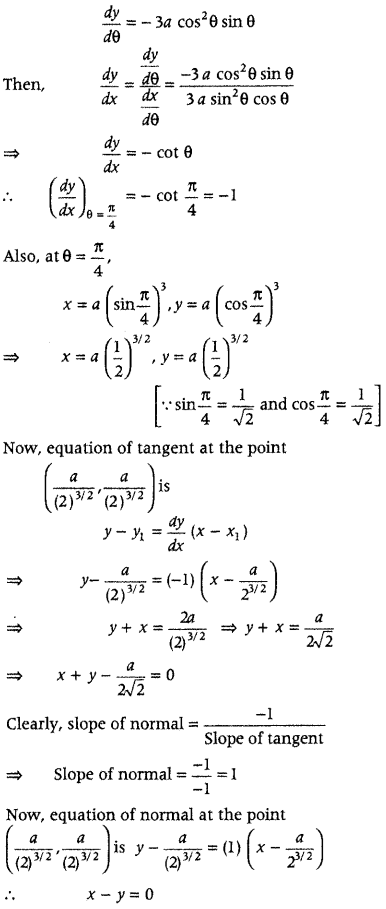
Question 10.
Find the equations of the tangent and normal to the curves \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1 at the point (√2a, b). (Delhi 2014)
Answer:
Given equation of curves is \(\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}\) = 1

On differentiating both sides w.r.t. x, we get
\(\frac{2 x}{a^{2}}-\frac{2 y}{b^{2}} \cdot \frac{d y}{d x}\) = 0 ⇒ \(\frac{d y}{d x}=\frac{b^{2} x}{a^{2} y}\)

Slope of the tangent at point (√2a, b) is
\(\left(\frac{d y}{d x}\right)_{(\sqrt{2} a, b)}=\frac{\sqrt{2} a b^{2}}{b a^{2}}=\frac{\sqrt{2} b}{a}\)

Hence, the equation of the tangent at point (√2a, b) is
y – b = \(\frac{\sqrt{2} b}{a}\)(x – √2a)
⇒ a (y- b) = √2 b (x – √2a)
⇒ ay – ab = √2 bx – 2ab
⇒ √2bx – ay – ab = 0

Now, the slope of the normal at point (√2a, b)
= \(\frac{-1}{\text { Slope of tangent }}=\frac{-1}{\sqrt{2} b / a}\)

Hence, the equation of the normal at point(√2a, b) is
(y – b) = \(-\frac{a}{\sqrt{2} b}\)(x – √2a)
⇒ √2b(y – b) = -a (x – √2a)
⇒ √2 by – √2 b ² = -ax + √2 a ²
∴ ax + √2by – √2 (a ² + b ² ) = 0

Question 11.
Find the points on curve y = x ³ – 11x + 5 at which equation of tangent is y = x – 11. (Delhi 2012C)
Answer:
First, find the slope of tangent to the given curve and of given equation of tangent, then equate them to get value of x. Put value of x in given curve to find required points.

Given, equation of curve is
y = x ³ – 11x + 5 ………(i)

Slope of the tangent at any point (x, y) is given by \(\frac{d y}{d x}\)
\(\frac{d y}{d x}\) = 3x – 11 ………….(ii)

Also, slope of the tangent y = x – 11 is 1.
∴ \(\frac{d y}{d x}\) = 1
⇒ 3x ² – 11 = 1 [frpm Eq. (i)]
⇒ 3x ² = 12 ⇒ x ² = 4 ⇒ x = ±2

When x = 2, then y = (2) ³ -11(2) + 5
= 8 – 22 + 5 = – 9
When x = – 2, then y = (-2) ³ -11 (-2) + 5
= -8 + 22 + 5 = 19
Since, the points (-2, 19) does not lies on the line y = x – 1
Hence, the required points on the curve are (2, -9).

Question 12.
Find the points on the curve x ² + y ² – 2x – 3 = 0 at which tangent is parallel to X-axis. (Delhi 2011)
Answer:
As tangent is parallel to X-axis, put \(\frac{d y}{d x}\) = 0 and find value of x from it. Then, put this value of x in the equation of the given curve and find value of y.

Given equation of curve is
x ² + y ² – 2x – 3 = 0

On differentiating both sides of Eq. (i) w.r.t. x, we get

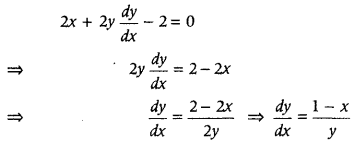
We know that, when a tangcnt to the curve is parallel to X-axis, then \(\frac{d y}{d x}\) = 0.

On putting \(\frac{d y}{d x}\) = 0, we get
1 – x = 0 ⇒ x = 1
Now, on putting x = 1 in Eq. (i), we get
1 + y ² – 2 – 3 = 0
y ² = 4 ⇒ y = ±2
Hence, the required points are (1, 2) and (1, -2).

Question 13.
Find the points on the curve y = x ³ at which the slope of the tangent is equal to y-coordinate of the point. (Foreign 2011)
Answer:
First, determine the derivative and put \(\frac{d y}{d x}\) = y and then find the value of x from it. Further, put this value of x in the equation of the given curve and find the value of y.

Given equation of curve is y = x ³ . …….(i)
On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = 3x ²

∴ Slope of tangent at any point (x, y) is
\(\frac{d y}{d x}\) = 3x ²

Now, given that Slope of tangent = y-coordinate of the point
⇒ \(\frac{d y}{d x}\) = y
⇒ 3x ² = y [∵\(\frac{d y}{d x}\) = 3x ² ]
⇒ 3x ² = x ³ [∵ y = x ³ ]
⇒ 3x ² – x ³ = 0 ⇒ x ³ (3 – x) = 0
⇒ Either x ² = 0 or 3 – x = 0
x = 0, 3

Now, on putting x = 0 and 3 in Eq. (i), we get
y = (0) ³ = 0 [at x = 0]
and y = (3) ³ = 27
Hence, the required points are (0, 0) and (3, 27).

Question 14.
Find the equation of tangent to curves
x = sin 3t, y = cos 2t at t = \(\frac{\pi}{4}\). (All India 2011C)
Answer:
We know that, the equation of tangent at the point (x ₁ , y ₁ ) is y – y ₁ =m(x – x ₁ ) …….(i)

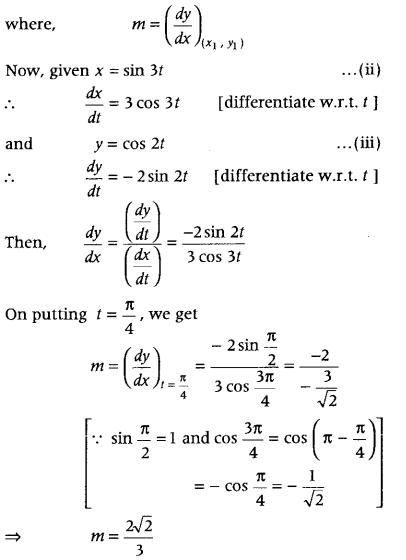
Also, to find (x ₁ , y ₁ ), we put t = \(\frac{\pi}{4}\) in given curves.
From Eqs. (ii) and (iii), we get

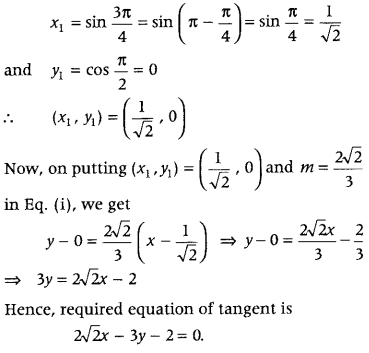
Question 15.
Find the equations of tangents to the curve y = (x ² – 1) (x – 2) at the points, where the curve cuts the X-axis. (All India 2011C)
Answer:
The curve cuts the X-axis, so put y = 0 and get the corresponding values of x. Further, differentiate and determine the slopes at different points. And then use the equation of tangent : y – y ₁ = m(x – x ₁ ).
Given equation of the curve is
y = (x ² -1) (x – 2) …(i)
Since, the curve cuts the X-axis, so at that point y- coordinate will be zero.
So, on putting y = 0, we get
(x ² – 1) (x – 2) = 0 ⇒ x ² = 1 or x = 2
∴ x = ±1 or 2 ⇒ x = -1, 1, 2

We know that, equation of tangent at the point (x ₁ , y ₁ ) is given by y – y ₁ = m(x – x ₁ ).
Here, we get three equations of tangents.
Equation of tangent at point (-1, 0) having slope (m ₁ ) = 6, is
y – 0 = 6 (x + 1)
⇒ y = 6x + 6 ⇒ 6x – y = -6
Equation of tangent at point (1, 0) having slope (m ₂ ) = – 2, is
y – 0 = -2(x – 1)
⇒ y = – 2x + 2
⇒ 2x + y = 2
and equation of tangent at point (2, 0) having slope (m ₃ ) = 3 is
y – 0 = 3(x – 2)
⇒ y = 3x – 6
∴ 3x – y = 6

Question 16.
Find the equation of tangent to the curve 4x ² + 9y ² = 36 at the point (3 cos θ, 2 sin θ). (Delhi 2011C)
Answer:
Given equation of curve is 4x ² + 9y ² = 36
On differentiating both sides w.r.t. x, we get
8x + 18y \(\frac{d y}{d x}\) = 0

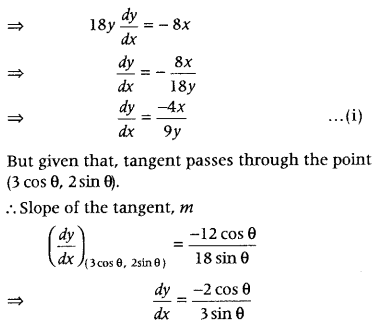
Now, equation of tangent at the point (3 cos θ, 2 sin θ) having slope, m = \(-\frac{2 \cos \theta}{3 \sin \theta}\) is
y – 2 sin θ = \(-\frac{2 \cos \theta}{3 \sin \theta}\)(x – 3 cos θ) [∵ y – y ₁ = m(x – x ₁ )]
⇒ 3y sin θ – 6 sin2 θ = – 2x cos θ + 6 cos2 θ
⇒ 2x cos θ + 3y sin θ – 6 (sin2 θ + cos2 θ) = 0
⇒ 2x cos θ + 3y sin θ – 6 = 0 [∵ sin2 θ + cos2 θ = 1]
which is the required equation of tangent.

Question 17.
Find the equation of tangent to the curve y = x ⁴ – 6x ³ + 13x ² – 10x + 5 at point x = 1, y = 0. (Delhi 2011C)
Answer:
Given equation of curve is
y = x ⁴ – 6x ³ + 13x ² – 10x + 5

On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = 4x ³ – 18x ² + 26x – 10

Slope of a tangent at point (1, 0) is
m = \(\left[\frac{d y}{d x}\right]_{x=1}\) = 4 – 18 + 26 – 10 = 2

∴ Equation of tangent at point (1,0) having slope 2 is
y – 0 = 2(x – 1)
⇒ y = 2x – 2
Hence, required equation of tangent is 2x – y = 2

Question 18.
Find the points on the curve
y = [x(x – 2)] ² , where the tangent is parallel to X-axis. (Delhi 2010)
Answer:
We have to find the points on the given curve where the tangent is parallel to X-axis. We know that, when a tangent is parallel to X-axis, then
\(\frac{d y}{d x}\) = 0
⇒ \(\frac{d}{d x}\)(x ² – 2x) ² = 0
⇒ 2(x ² – 2x)(2x – 2) = 0
⇒ x = 0, 1, 2
When x = 0, then y = [0(-2)] ² = 0
When x = 1, then y = [1 – 2(1)] ² = 1
When x = 2, then y = [2 ² – 2 × 2] ² = 0
Hence, the tangent is parallel to X-axis at the points (0, 0), (1, 1) and (2, 0).

Question 19.
Find the equation of tangent to the curve y = \(\frac{x-7}{x^{2}-5 x+6}\) at the point, where it cuts the X-axis. (All India 2010C, 2010)
Answer:
Given equation of curves is
y = \(\frac{x-7}{x^{2}-5 x+6}\) ……….(i)

On differentiating both sides w.r.t. x, we get

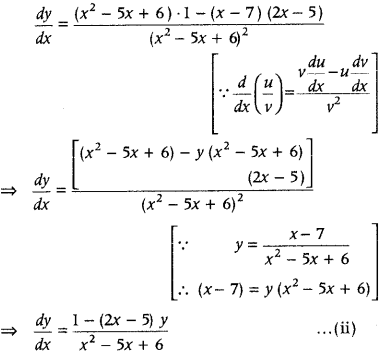
[dividing numerator and denominator by x ² – 5x + 6]
Also, given that curve cuts X-axis, so its y-coordinate is zero.
Put y = 0 in Eq. (i), we get
\(\frac{x-7}{x^{2}-5 x+6}\) = 0
⇒ x = 7
So, curve passes through the point (7, 0).
Now, slope of tangent at (7, 0) is
m = \(\left(\frac{d y}{d x}\right)_{(70)}=\frac{1-0}{49-35+6}=\frac{1}{20}\)

Hence, the required equation of tangent passing through the point (7, 0) having slope 1/20 is
y – o = \(\frac{1}{20}\)(x – 7)
⇒ 20y = x – 7
∴ x – 20y = 7

Question 20.
Find the equations of the normal to the curve y = x ³ + 2x + 6, which are parallel to line x + 14y + 4 = 0. (Delhi 2010)
Answer:
First, find the slope of normal to curve, i.e. \(\frac{-1}{d y / d x}\) and put them equal to the slope of line, simplify them and find the values of x and y. Further, use the equation y – y ₁ = Slope of normal (x – x ₁ ).

Given equation of curve is
y = x ² + 2x + 6 ……..(i)
and the given equation of line is
x + 14y + 4= 0

On differentiating both sides of Eq. (i) w.r.t. x, we get
\(\frac{d y}{d x}\) = 3x ² + 2
Slope of normal = \(\frac{-1}{\left(\frac{d y}{d x}\right)}=\frac{-1}{3 x^{2}+2}\)

Also, slope of the line x + 14y + 4 = 0 is – \(\frac{1}{14}\) [∵ slope of the line Ax + By + C = 0 is – \(\frac{A}{B}\)]
We know that, if two lines are parallel, then their slopes are equal.
∴ \(-\frac{1}{3 x^{2}+2}=-\frac{1}{14}\)
⇒ 3x ² + 2 = 14
⇒ 3x ² = 12 ⇒ x ² = 4
⇒ x = ± 2

When x = 2, then from Eq. (i),
y = (2) ³ + 2(2) + 6 = 8 + 4 + 6 = 18
and when x = – 2, then from Eq. (i),
y = (-2) ³ + 2(-2) + 6 = -8 – 4 + 6 = – 6

∴ Normal passes through (2, 18) and (-2, -6).
Also, slope of normal = – \(\frac{1}{14}\)
Hence, equation of normal at point (2, 18) is
y – 18 = – \(\frac{1}{14}\)(x – 2)
⇒ 14y – 252 = – x + 2
⇒ x + 14 y = 254

and equation of normal at point (-2, -6) is
y + 6 = – \(\frac{1}{14}\) (x + 2)
⇒ 14y + 84 = -x – 2
⇒ x + 14y = -86
Hence, the two equations of normal are
x + 14y = 254 and x + 14y = – 86.

Question 21.
Find the angle of intersection of the curves y ² = 4ax and x ² = 4by. (Foreign 2016)
Answer:
Given equations of curves are
y ² = 4ax …(i)
and x ² = 4 by … (ii)
Clearly, the angle of intersection of curves (i) and (ii) is the angle between the tangents to the curves at the point of intersection.
So, let us first find the intersection point of given curves.

On substituting the value of y from Eq. (ii) in Eq. (i), we get
\(\left(\frac{x^{2}}{4 b}\right)^{2}\) = 4ax
⇒ \(\frac{x^{4}}{16 b^{2}}\) = 4ax ⇒ x ⁴ = 64ab ² x
⇒ x ⁴ – 64ab ² x = 0
⇒ x(x ² – 64ab ² ) = 0
x = 0 or x = 4a ^1/3 b ^2/3
Clearly, when x = 0, then from Eq. (i), y = 0 and when x = 4a ^1/3 b ^2/3 , then from Eq. (i),
y ² =16a ^4/3 b ^2/3 ⇒ y = 4a ^2/3 b ^1/3

Thus, the points of intersection are (0, 0) and (4a ^1/3 b ^2/3 , 4a ^2/3 b ^1/3 ).
Now, let us find the angle of intersection at (0, 0) and (4a ^1/3 b ^2/3 , 4a ^2/3 b ^1/3 ).
Let be the slope of tangent to the curve (i) and m ₂ be the slope of tangent to the curve (ii).

Angle of intersection at (0, 0)

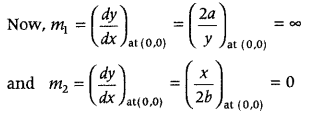
⇒ Tangent to the curve (i) is parallel to 7-axis and tangent to the curve (ii) is parallel to X-axis.
∴ Angle between these curves two is \(\frac{\pi}{2}\).
⇒ The angle of intersection of the curves is \(\frac{\pi}{2}\)

Angle of intersection at (4a ^1/3 b ^2/3 , 4a ^2/3 b ^1/3 )

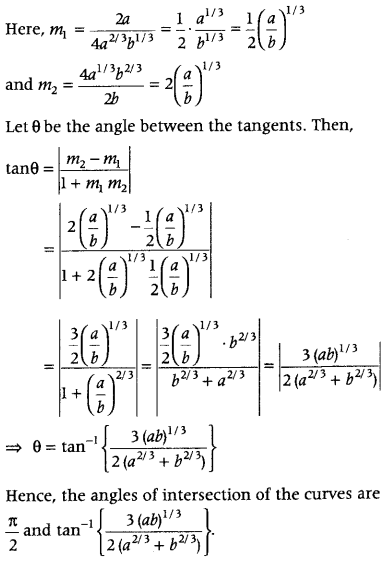
Question 22.
Find the equation of tangents to the curve y = cos(x + y), -2π ≤ x ≤ 2π that are parallel to the line x + 2y = 0. (Foreign 2016)
Answer:
Given equation of curve is y = cos(x + y), -2π ≤ x ≤ 2π …………(i)
and equation of line is x + 2y = 0 …….(ii)
⇒ y = –\(\frac{1}{2}\)x
Clearly, slope of tangents to the curve is –\(\frac{1}{2}\).
Let (x ₁ , y ₂ ) be the point of contact, then we have
y ₁ = cos(x ₁ + y ₁ ) [from Eq. (i)] …(iii)

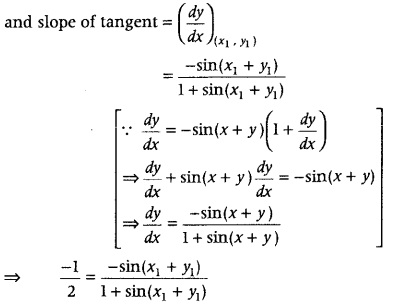
⇒ 1 + sin(x ₁ + y ₁ ) = 2sin(x ₁ + y ₁ )
⇒ sin(x ₁ + y ₁ ) = 1 …(iv)

On squaring and adding Eqs. (iii) and (iv), we get
cos ² (x ₁ + y ₁ ) + sin ² (x ₁ + y ₁ ) = 1 + y ₁ ²
1 + y ² ₁ = 1 ⇒ y ² ₁ = o ⇒ y ₁ = o

On putting y ₁ = 0 in Eq. (iii), we get cosx ₁ = 0
⇒ x ₁ = \(\frac{\pi}{2}, \frac{3 \pi}{2}, \frac{-\pi}{2}, \frac{-3 \pi}{2}\) [∵ -2π ≤ x ≤ 2π]
But only x ₁ = \(\frac{\pi}{2}\) and \(\frac{-3 \pi}{2}\) satisfy Eq. (iv).

Hence, the points of contact are (\(\frac{\pi}{2}\), o) and (\(\frac{-3 \pi}{2}\), 0)
∴ Equations of tangents are
y – 0 = –\(\frac{1}{2}\)(x – \(\frac{\pi}{2}\))
and y -0 = –\(\frac{1}{2}\)(x + \(\frac{-3 \pi}{2}\))

Question 23.
Find the value of p for which the curves x ² = 9p (9 – y) and x ² = p (y + 1) cut each other at right angles. (All India 2015)
Answer:
Given equations of curves are
x ² = 9p (9 – y) …….(i)
and x ² = p (y + 1) ………….(ii)

As, these curves cut each other at right angle, therefore their tangent at point of intersection are perpendicular to each other.
So, let us first find the point of intersection and slope of tangents to the curves.
From Eqs. (i) and (ii), we get
9p(9 – y) =p(y + 1)
∴ 9(9 – y) = y + 1
[∵ p ≠ 0, as if p = 0, then curves becomes straight, which will be parallel]
⇒ 81 – 9y = y + 1 ⇒ 80 = 10y ⇒ y = 8

On substituting the value of yin Eq. (i),we get
x ² = 9p ⇒ x = + 3
Thus, the point of intersection are (3√p, 8) and (-3√p, 8)

Now, consider Eq.(i),we get
\(\frac{x^{2}}{9 p}\) = 9 – y ⇒ y = 9 – \(\frac{x^{2}}{9 p}\)

On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{-2 x}{9 p}\) ……(iii)

From Eq. (ii), we get \(\frac{x^{2}}{p}\) = y + 1
⇒ y = \(\frac{x^{2}}{p}\) – 1

On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{2 x}{p}\) ………(iv)

Now, for intersection point (3√p, 8), we have slope of tangent to the first curve
= \(\frac{-2(3 \sqrt{p})}{9 p}=\frac{-6 \sqrt{p}}{9 p}\) [using Eq. (iii)]

and slope of tangent to the second curve
= \(\frac{2(3 \sqrt{p})}{p}=\frac{6 \sqrt{p}}{p}\) [using Eq. (iv)]

∵ Tangents are perpendicular to each other.
Then,
Slope of first curve x Slope of second curve = -1
∴ \(\frac{-6 \sqrt{p}}{9 p} \times \frac{6 \sqrt{p}}{p}\) = -1 ⇒ \(\frac{4}{p}\) = 1 ⇒ p = 4

And for intersection point (3√p, 8), we have slope of tangent to the first curve
= \(\frac{-2(-3 \sqrt{p})}{9 p}=\frac{6 \sqrt{p}}{9 p}\) [using Eq. (iii)]

and slope of tangent to the second curve
= \(\frac{2(-3 \sqrt{p})}{p}=\frac{-6 \sqrt{p}}{p}\) [using Eq. (iv)]

Tangents are perpendicular to each other. Then,
\(\frac{6 \sqrt{p}}{9 p} \times \frac{-6 \sqrt{p}}{p}\) = -1 [∵ m ₁ m ₂ = -1]
⇒ \(\frac{4}{p}\) = 1 ⇒ p = 4
Hence, the value of p is 4.

Question 24.
Find the equations of the tangent to the curve y = x ² – 2x + 7 which is
(i) parallel to the line 2x – y + 9 = 0.
(ii) perpendicular to the line 5y – 15x = 13. (Delhi 2014C)
Answer:
Given equation of curve is
y = x ² – 2x + 7

On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}\) = 2x – 2

(i) Given, equation of the line is 2x – y + 9 = 0
⇒ y = 2x + 9
which is of the form y = mx + c.

∴ Slope of the line is m = 2
If a tangent is parallel to the line, then slope of tangent is equal to the slope of the line.
Therefore, \(\frac{d y}{d x}\) = m ⇒ 2x – 2 = 2 ⇒ x = 2
When x = 2, then from Eq. (i), we get
y = 2 ² – 2 × 2 + 7 ⇒ y = 7
The point on the given curve at which tangent is parallel to given line is (2, 7) and the equation of the tangent is
y – 7 = 2(x – 2) [∵ y – y ₁ =m(x- x ₁ )]
⇒ 2x – y + 3 = 0
Hence, the equation of the tangent line to the given curve which is parallel to line 2x – y + 9 = 0 is y – 2x – 3 = 0.

(ii) The equation of the given line is 5y – 15x = 13
⇒ y = \(\frac{15 x+13}{5}\) = 3x + \(\frac{13}{5}\)
which is of the form y = mx + c

∴Slope of the given line is 3.
If a tangent is perpendicular to the line 5y – 15x = 13.
Then, the slope of the tangent = –\(\frac{1}{3}\)

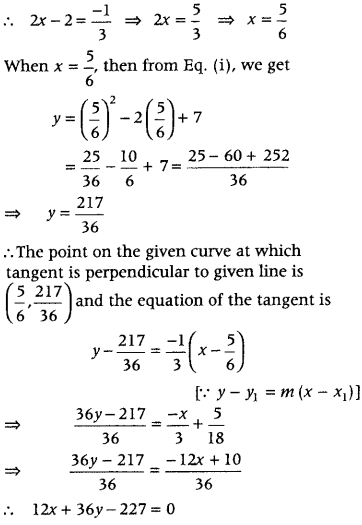
Hence, the equation of the tangent line to the given curve which is perpendicular to the line 5y – 15x = 13 is 36y + 12x – 227 = 0.

Question 25.
Find the equation of the normal at a point on the curve x ² = 4y, which passes through the point (1, 2). Also, find the equation of the corresponding tangent. (Delhi 2013)
Answer:
Given curve is x ² = 4y.
On differentiating both sides w.r.t. x,we get
2x = 4\(\frac{d y}{d x}\) ⇒ \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)
Let (h, k) be the coordinates of the point of contact of the normal to the curve x2 = 4y. Then, slope of the tangent at (h, k) is given by
\(\left(\frac{d y}{d x}\right)_{(h, k)}=\frac{h}{2}\)
and slope of the normal ay (h, k) = \(\frac{-1}{d y / d x}=\frac{-2}{h}\)

Therefore, the equation of normal at (h, k) is
y – k = \(\frac{-2}{h}\)(x – h) ………….(i)
[∵ Equation of normal in slope form is y – y ₁ = \(\frac{-1}{m}\)(x – x ₁ )]
Since, it passes through the point (1, 2), so on putting x =1 and y = 2, we get
2 – k = \(\frac{-2}{h}\)(1 – h)
⇒ k = 2 +
Since, (h, k) also lies on the curve x ² = 4y, therefore h ² = 4k ………(iii)

On solving Eqs.(ii) and (iii), we get
h = 2 and k = 1

Substituting the values of h and k in Eq.(i), the required equation of normal is
y – 1 = \(\frac{-2}{2}\)(x – 2) ⇒ x + y = 3

Now, equation of tangent at (h, k) is
y – k = \(\frac{h}{2}\)(x – h)

On putting h = 2 and k = 1, we get
y – 1 = \(\frac{2}{2}\)(x – 2) ⇒ y – 1 = x – 2
∴ y = x – 1

Question 26.
Find the equations of tangents to the curve 3x ² – y ² = 8, which passes through the point [\(\frac{4}{3}\), 0 ]. (All India 2013)
Answer:
First, differentiate the given curve with respect to x and determine \(\frac{d y}{d x}\). Then, find the equation of tangent at (x, y,}. Now, as this equation is passes through given point (x0, y0), so this point will satisfy the tangent and curve also. Further, simplify it and get the required equations of tangent.

Given equation of curve is
3x ² – y ² = 8

On differentiating both sides w.r.t. x, we get

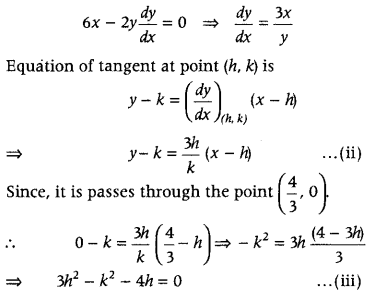
Also, the point (h, k) satisfy the Eq. (i), so we get
3h ² – k ² = 8 ……(iv)

Now, on solving Eqs. (iii) and (iv), we get
4h = 8
⇒ h = 2

On putting h = 2 in Eq. (iv), we get
3 (2) ² – k ² = 8
⇒ k ² = 4
⇒ k = ±2

Now, putting the values of h and k in Eq. (h), we get
⇒ y = (±2) = \(\frac{3(2)}{\pm 2}\)(x – 2)
⇒ y + 2 = ±3(x – 2)
⇒ y = ± 3(x – 2) ± 2
⇒ y = ± {3(x – 2) + 2}
⇒ y = ± (3x – 6 + 2)
⇒ y = ± (3x – 4)
Hence, y = – 3x + 4 and y = 3x – 4 are two required equations of tangent.

Question 27.
Find all the points on the curve y = 4x ³ – 2x ⁵ at which the tangent passes through the origin. (Delhi 2013C)
Answer:
Given curve is y = 4x ³ – 2x ⁵ . ………(i)

Let any point on the curve be (x ₁ ,y ₁ ). So, it satisfies Eq. (i).
∴ y ₁ = 4x ₁ ³ – 2x ₁ ⁵ ………(ii)

On differentiating both sides of Eq. (i), we get
\(\frac{d y}{d x}\) = 12x ² – 10x ⁴

Equation of tangent at point (x ₁ , y ₁ ) is
y – y ₁ = \(\left(\frac{d y}{d x}\right)_{\left(x_{1}, y_{1}\right)}\) (x – x ₁ )
⇒ y – y ₁ = [12(x ₁ ) ² – 10(x ₁ ) ⁴ ](x – x ₁ )

Since, it passes through the origin.
∴ 0 – y ₁ = (12x ₁ ² – 10x ₁ ⁴ )(0 – x ₁ )
⇒ y ₁ = (12x ₁ ² – 10x ₁ ⁴ )x ₁ ………(iii)

From Eqs. (ii) and (iii), we get
(12x ² ₁ – 10x ⁴ ₁ )x ₁ = 4x ₁ ³ – 2x ₁ ⁵
⇒ 2x ₁ ³ (6 – 5x ₁ ² ) = 2x ₁ ³ (2 – x ₁ ² )
⇒ 2x ₁ ³ (4 – 4x ₁ ² ) = 0
⇒ x ₁ = 0 or 4 – 4x ₁ ² = 0
∴ x ₁ = 0 or x ₁ = 1

On putting the values of x, = 0,1 and -1 respectively in Eq. (ii), we get
At x ₁ = 0, y ₁ = 0
At x ₁ = 1, y ₁ = 4(1) ³ -2(1) ⁵ = 4 – 2 = 2
and at x ₁ = (-1),
y ₁ = 4(-1) ³ – 2(-1) ⁵
= 4 (-1) – 2 (-1) = -4+ 2 = -2
Hence, all points on the curve at which the tangent passes through origin, are (0, 0), (1, 2) and (-1,-2).

Question 28.
Prove that the curves x = y ² and xy = k cut at the right angles, if 8k ² = 1. (Delhi 2013C)
Answer:
Given equations of curves are
x = y ² …(i)
and xy = k …(ii)

Let the curves (i) and (ii) cut at right angle.
Let us first find the point of intersection of given curves.
On substituting the value of x from Eq. (i) in Eq. (ii), we get
y ³ = k ⇒ y = k ^1/3
On substituting y = k ^1/3 in Eq. (ii), we get
x = k ^2/3
Thus, the point of intersection is (k ^1/3 , k ^2/3 ).
Now, let m ₁ be the slope of tangent to the curve (i) and m ₂ be the slope of tangent to the curve (ii).

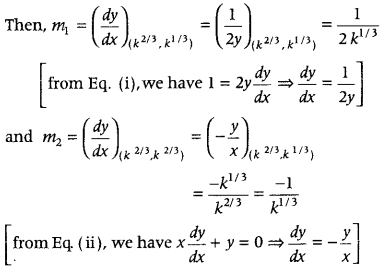
Since, the curves (i) and (ii) cut at right angle.
∴ Angle between the tangents to the curves at the point of intersection is \(\frac{\pi}{2}\), i.e. tangents to the curves are perpendicular to each other.
⇒ m ₁ .m ₂ = -1
⇒ \(\left(\frac{1}{2 k^{1 / 3}}\right)\left(\frac{-1}{k^{1 / 3}}\right)\) = -1
⇒ \(\frac{1}{2 k^{2 / 3}}\)= 1 ⇒ 2k ^2/3 = 1

On cubing both sides, we get
8k ² = 1
Hence Proved.

Question 29.
Prove that all normals to the curves x = a cos t + at sin t and y = a sin t – at cos t are at a constant distance ‘a’ from the origin. (All India 2013C)
Answer:
Given equations of curves are
x = a cost + at sin t and y = asin t – at cost

On differentiating x and y separately w.r.t. t, we get
\(\frac{d x}{d t}\) = -asin t + a(t cost + sin t)
= -a sin t + a tcos t+ a sin t = at cost
and \(\frac{d y}{d t}\) = acos t – a[t(-sin t) + cos t)]
= a cost + at sin t – acost = at sin t

Now \(\frac{d y}{d x}=\frac{\frac{d y}{d t}}{\frac{d x}{d t}}=\frac{a t \sin t}{a t \cos t}\) = tan t
= Slope of normal at any point t = \(\frac{-1}{\tan t}\) = -cot t

Now, equation of normal at any point t is given by
y – (asin t – at cos t) = – cot t[x – (a cos t + atsint)]
⇒ y – asin t + at cos t = \(\frac{-\cos t}{\sin t}\) (x – acost – at sin t)
⇒ y sint – a sin ² t + at cost sint = -x cost + acos ² t + at sint cost
⇒ x cost + y sint = a(cos ² t + sin ² t)
⇒ x cost + ysint = a [∵ sin ² θ + cos ² θ = 1]
∴ xcos t + ysin t – a = 0
Now, the distance of normal from the origin is given by
\(\frac{|0 \cdot \cos t+0 \cdot \sin t-a|}{\sqrt{\cos ^{2} t+\sin ^{2} t}}=\frac{|-a|}{\sqrt{1}}\) = a

Question 30.
Find the equations of tangent and normal to the curve x = 1 – cos θ, y = θ – sin θ at θ = \(\frac{\pi}{4}\)
Answer:
First, differentiate the given curve with respect to and then determine \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{4}\). Further, use the formula, equation of tangent at (x ₁ , y ₁ ) is y – y ₁ = m(x – x ₁ )
and equation of normal at (x ₁ , y ₁ ) is
y – y ₁ = –\(\frac{1}{m}\) (x – x ₁ ).

Given curves are x = 1 – cos θ and y = θ – sin θ.
On differentiating x and y separately w.r.t. θ, we get

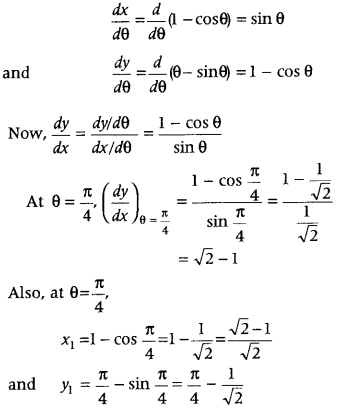
We know that, equation of tangent at (x ₁ , y ₁ ) having slope m, is given by

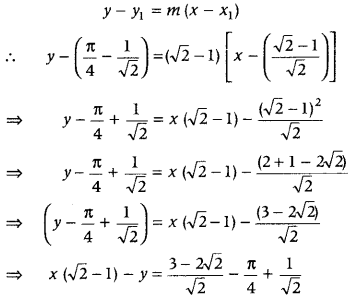
Hence, the equation of tangent is
x(√2 – 1) – y = \(\frac{12-8 \sqrt{2}-\sqrt{2} \pi+4}{4 \sqrt{2}}\)
⇒ x(8 – 4√2) – 4√2y = (16 – √2π – 8√2)

Also, the equation of normal at (x ₁ , y ₁ ) having slope –\(\frac{1}{m}\) is given by

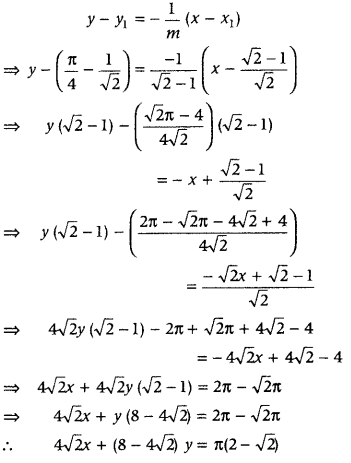
Maxima and Minima

Question 1.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when depth of the tank is half of its width. If the cost is to he borne by nearby settled lower income families, for whom water will be provided. (CBSE 2018; All India 2010 C)
Answer:
Let x be the length of a side of square base and y be the length of vertical side. Also, let V be the given quantity of water.

Then, V = x ² y …(i)
[∵ volume of cuboid = L × B × H]
Clearly, the surface area, S = 4xy + x ²
= 4x.\(\frac{V}{x^{2}}\) + x ² [using Eq. (i)]
⇒ S(x) = \(\frac{4 V}{x}\) + x ²

Now, on differentiating both sides w.r.t. x, we get

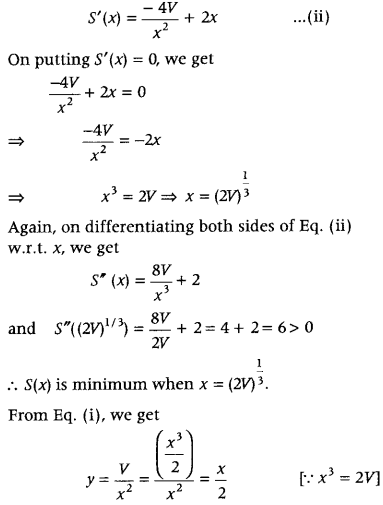
Thus, the cost of material will be least when depth of the tank is half of its width.

Question 2.
The sum of the perimeters of a circle and square is k, where k is some constant. Prove that the sum of their areas is least, when the side of the square is double the radius of the circle. (Delhi 2014C)
Answer:
Let r be the radius of circle and x be the side of a square. Then, given that
Perimeter of square + Perimeter of circle
= k (constant)
i.e. 4x + 2πr = k ⇒ x = \(\frac{k-2 \pi r}{4}\) ……(i)

Let A denotes the sum of their areas.
∴ Area, A = area of a square + area of circle
∴ A = x ² + πr ² …(ii)

On putting the value of x from Eq. (i) in Eq.(ii), we get

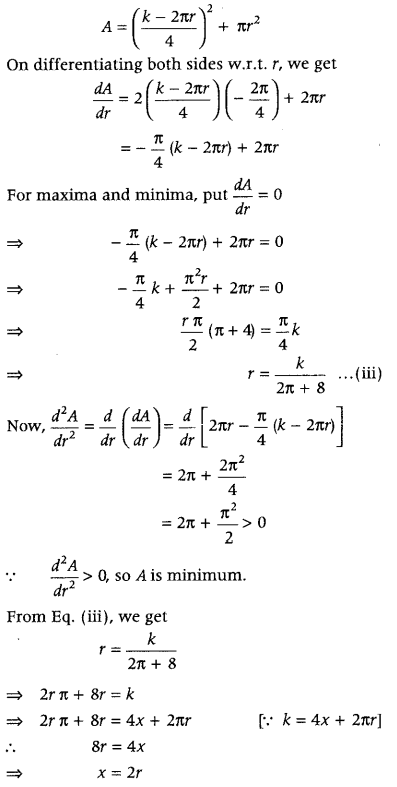
i.e. Side of square = double the radius of circle
Hence, sum of area of a circle and a square is least, when side of square is equal to diameter of circle or double the radius of circle.
Hence Proved.

Question 3.
A tank with rectangular base and rectangular sides, open at the top is to be constructed, so that its depth is 2 m and volume is 8 m ³ . If building of tank cost ₹ 70 per sq m for the base and ₹ 45 per sq m for sides. What is the cost of least expensive tank? (Delhi 2019)
Answer:
Let x m be the length, y m be the breadth and h=2m be the depth of the tank.
Let ₹ H be the total cost for building the tank. Now, given that h = 2 m and volume of tank = 8 m ³ .
Clearly, area of the rectangular base of the tank
= length × breadth = xy m ²

and the area of the four rectangular sides
= 2 (length + breadth) × height
= 2 (x + y) × 2= 4 (x + y) m ²

∴ Total cost, H = 70 × xy + 45 × 4 (x + y)
⇒ H = 70xy + 180 (x + y) …………(i)

Also, volume of tank = 8 m ³
⇒ l × b × h = 8 ⇒ x × y × 2 = 8 ⇒ y = \(\frac{4}{x}\) …..(ii)

On putting the value of y from Eq. (ii) in Eq. (i), we get

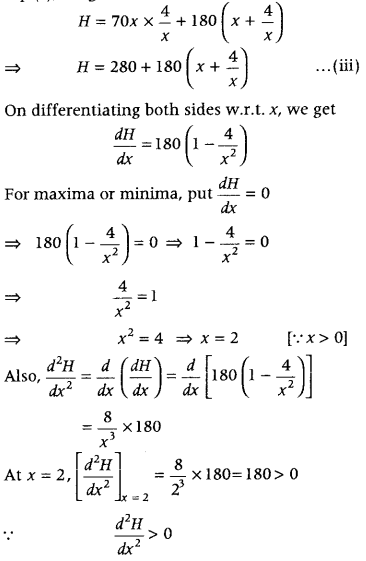
⇒ H is least at x = 2.
Also, the least cost = 280 + 180(2 + \(\frac{4}{2}\))
[put x = 2in Eq. (iii) to get least cost H]
= 280 + 180 × 4 = 280 + 720 = ₹ 1000
Hence, the cost of least expensive tank is ₹ 1000

Question 4.
Prove that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius R is \(\frac{2 R}{\sqrt{3}}\). Also, find the maximum volume. (All India 2019,2014,2012C, 2011: Delhi 2013)
Answer:
Let h be the height and a be the radius of base of cylinder inscribed in the given sphere of radius (R).

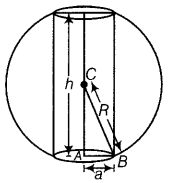
In ΔABC, AB ² = AC ² + BC ² [by Pythagoras theorem]

⇒ V is maximum.
Hence, the required height of cylinder is V
Hence proved.
Now, maximum volume of cylinder, V

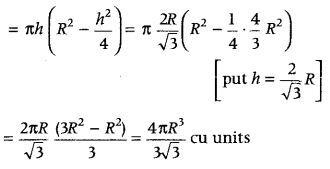
Question 5.
Find the point on the curve y ² = 4x, which is nearest to the point (2, – 8). (All India 2019)
Answer:
Given, equation of curve is y ² = 4x.
Let P(x, y) be a point on the curve, which is nearest to point A(2, – 8).
Now, distance between the points A and P is given by

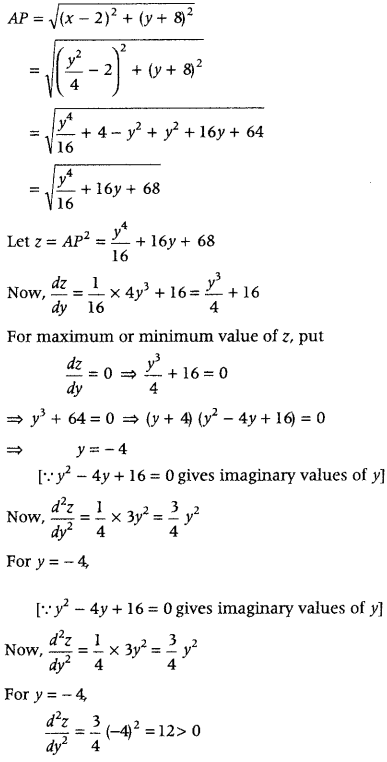
Thus, z is minimum when y = – 4.
Substituting y = -4 in equation of the curve y ² = 4x; we obtain x = 4.
Hence, the point (4, – 4) on the curve y ² = 4x is nearest to the point (2, – 8).

Question 6.
Show that the altitude of the right circular cone of maximum volume that can he inscribed in a sphere of radius r is \(\frac{4r}{3}\)
Also, find the maximum volume in terms of volume of the sphere. (Delhi 2019, 2016)
Or
Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius r is \(\frac{4r}{3}\). Also, show that the maximum volume of the cone is \(\frac{8}{27}\) of the volume of the sphere. (All India 2014)
Answer:
Let R be the radius and h be the height of the cone, which inscribed in a sphere of radius r.
∴ OA = h – r

In ΔOAB, by Pythagoras theorem, we have
r ² = R ² + (h – r) ²
⇒ r = R ² + h ² + r ² – 2rh
⇒ R ² = 2rh – h ² ……….(i)

The volume of sphere = \(\frac{4}{3}\) πr ³

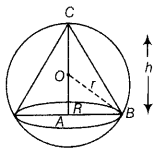
and the volume V of the cone,
V = \(\frac{1}{2}\) πR ² h
⇒ V = \(\frac{1}{2}\) πh (2rh – h ² ) [from Eq. (i)]
⇒ V = \(\frac{1}{2}\) π (2rh ² – h ³ ) …..(ii)

On differentiating both sides of Eq, (ii) w.r.t. h, we get

⇒ V is maximum at h = \(\frac{4r}{3}\).
Hence proved.

On substituting the value of h in Eq. (ii), we get

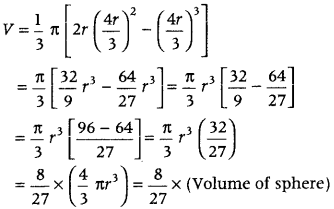
Hence, maximum volume of the cone is \(\frac{8}{27}\) of the volume of the sphere.

Question 7.
A window is of the form of a semi-circle with a rectangle on its diameter. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening. (CBSE 2018 C; All India 2017,2011; Foreign 2014)
Or
A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. ,Find the dimensions of the window to ‘ admit maximum light through the whole j opening. (All India 2017)
Answer:
Let 2x be the length and y be the width of the window.
Then, radius of semicircular opening = x m

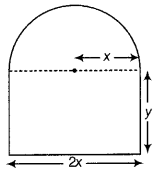
Since, perimeter of the window is 10 m.
∴ 2x + y + y + \(\frac{2 \pi x}{2}\) = 10
⇒ 2x + 2y + πx = 10
⇒ x(π + 2) + 2y = 10
⇒ y = \(\frac{10-x(\pi+2)}{2}\) ……(i)

Note that, to admit maximum light, area of window should be maximum.
Here, area of window
A = area of rectangle + area of semicircular region
= 2x × y + \(\frac{1}{2}\)πx ²
⇒ A = 2x\(\left(\frac{10-x(\pi+2)}{2}\right)\) + \(\frac{1}{2}\) πx ² [from Eq. (i)]
⇒ A = 10x – x ² (π + 2) + \(\frac{1}{2}\) πx ²

On differentiating both sides w.r.t. x, we get dA
\(\frac{d A}{d x}\) = 10 – 2x (π + 2) + πx
= 10- 2x π – 4x + πx
= 10 – πx – 4x ……(iii)

For maximum, Put \(\frac{d A}{d x}\) = 0
⇒ 10 = πx + 4x
⇒ x = \(\frac{10}{\pi+4}\)

Again, on differentiating both sides of Eq. (ii), we get

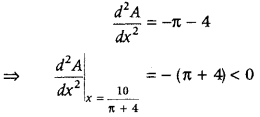
Thus, area is maximum when x = \(\frac{10}{\pi+4}\)
Now, on substituting the value of x in Eq. (i), we get

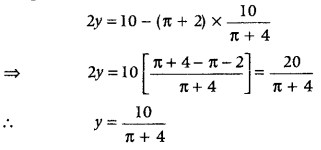
Hence, length of window = \(\frac{20}{\pi+4}\)m and width of windows = \(\frac{10}{\pi+4}\)m, to admit maximum light through the whole opening.

Question 8.
Show that the surface area of a closed cuboid with square base and given volume is minimum, when it is a cube. (All India 2017)
Answer:
Let V be the fixed volume of a closed cuboid with length x, breadth x and height y.
Then, V = x × x × y
⇒ y = \(\frac{V}{x^{2}}\) …………(i)

Let S be its surface area.
Then, S = 2(x ² + xy + xy)

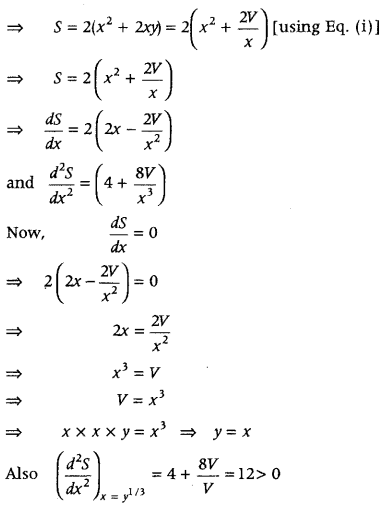
So, S is minimum
when length = x, breadth = x and height = x, when it is cube.

Question 9.
AB is the diameter of a circle and C is any point on the circle. Show that the area of AABC is maximum, when it is an isosceles triangle. (All India 2017, 2014C)
Answer:
Let AC = x,BC = y and r be the radius of circle.
Also, ∠C= 90° [v angle made in semi-circle is 90°]
In ΔABC, we have
(AB) ² = (AQ) ² + (BQ) ²
⇒ (2r) ² = (x) ² + (y) ²
⇒ 4r ² = x ² + y ² ….(i)

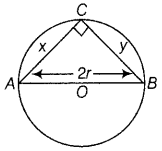
We know that,
Area of ΔABC,(A) = \(\frac{1}{2}\)x.y
On squaring both sides, we get

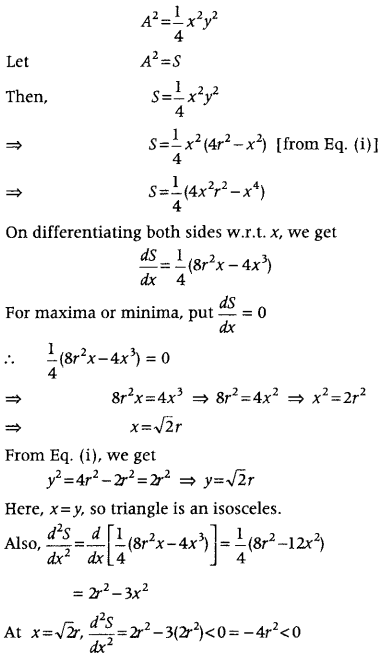
Hence, area is maximum when triangle is an isosceles.
Hence proved

Question 10.
If the sum of lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum, when the angle between them is \(\frac{\pi}{3}\). (Delhi 2017; All India 2014)
Answer:
Let us consider a right angled triangle with base = x and hypotenuse =y.
Let x + y = k, where k is a constant.
Let θ be the angle between the base and the hypotenuse.
Let A be the area of the triangle, then

Hence, the area of triangle is maximum, when θ = \(\frac{\pi}{3}\).
Hence proved.

Question 11.
A metal box with a square base and vertical sides is to contain 1024 cm ³ . The material for the top and bottom costs ₹ 5 per cm ² and the material for the sides costs ₹ 2.50 per cm ² . Find the least cost of the box. (Delhi 2017)
Answer:
Given, volume of the box= 1024 cm ³ . Let length of the side of square base be x cm and height of the box be y cm.

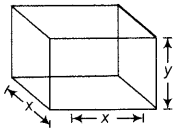
Volume of the box, V = x ² .y = 1024
⇒ x ² y = 1024
⇒ y = \(\frac{1024}{x^{2}}\)

Let C denotes the cost of the box.
C = 2x ² × 5 + 4xy × 2.50
= 10x ² + 10xy = 10x (x + y)
= 10x(x + \(\frac{1024}{x^{2}}\))
= 10x ² + \(\frac{10240}{x}\) ……..(i)

On differentiating both sides w.r.t. x, we get

For x = 8, cost is minimum and the corresponding least cost of the box
C (8) = 10. 8 ² + \(\frac{10240}{8}\) = 640 + 1280 = 1920
Hence, least cost of the box is ₹s 1920.

Question 12.
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is cos ^-1 1/√3. (All India 2016; Delhi 2014)
Answer:
Let θ be the semi-vertical angle of the cone.
It is clear that θ ∈ (0, \(\frac{\pi}{2}\))
Let r, h and l be the radius, height and the slant height of the cone, respectively.

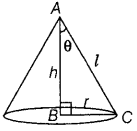
Since, slant height of the cone is given, so consider it as constant.
Now, in ΔABC, r = l sin θ and h = l cos θ
Let V be the volume of the cone.

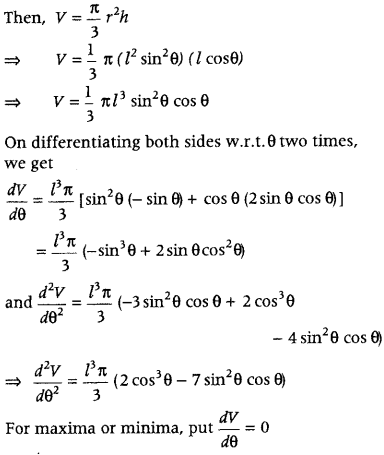
⇒ sin ³ θ = 2sinθ cos ² θ
⇒ tan ² θ = 2
⇒ tan θ = √2
⇒ θ = tan ^-1 √2

Now, when θ = tan ^-1 √2, then tan ² θ = 2
⇒ sin ² θ = 2cos ² θ

Now, we have

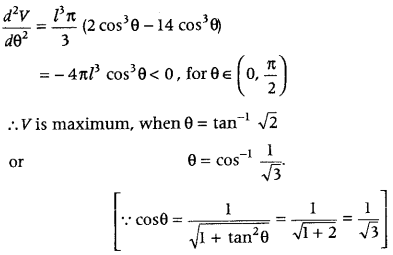
Hence, for given slant height, the semi-vertical angle of the cone of maximum volume is cos ^-1 \(\frac{1}{\sqrt{3}}\).

Question 13.
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed, is 6√3r. (All India 2016)
Answer:
Let ABC be the given isosceles triangle, with AB = AC.

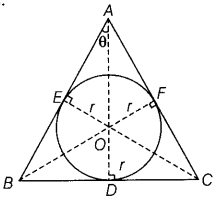
Clearly, OD ⊥ BC, OF ⊥ AC, OE ⊥ AB [∵ radius is perpendicular to the tangent at the point of contact]
and BD = BE, CD = CF, AE = AF [∵ tangents from an external point to a circle are equal in length]
Since, AD is an altitude of isosceles ΔABC, Therefore, BD = CD [∵ in an isosceles triangle, altitude from common vertex of equal sides bisect the third side]
⇒ BD = BE = CF = CD [∵ BE = BD and CD = CF]

Now, perimeter (P) of ΔABC = AB + BC + AC
= AE + BE + BD + DC + AF + FC
= (AE +AF) + (BE + BD + DC + FC)
= 2AE + 4BD …(i)

Consider ΔOEA, in this we have
AE = \(\frac{O E}{\tan \theta}=\frac{r}{\tan \theta}\) and OA = \(\frac{r}{\sin \theta}\)
and in ΔADB we have BD = AD tan θ
= (AO + OD) tanθ
= [\(\frac{r}{\sin \theta}\) + r)tan θ
Now, P = 2.\(\frac{r}{\sin \theta}\) + 4(\(\frac{r}{\sin \theta}\) + r)tan θ [From Eq. (i)]
⇒ P(θ) = r(2 cot θ + 4 sec θ + 4 tan θ) …….(ii)

On differentiating both sides w.r.t. θ, we get
P'(θ) = r(-2cosec ² θ + 4secθ tanθ + 4sec ² θ) …(iii)

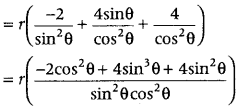
Now, put P'(θ) = 0
⇒ -2cos2θ + 4sin3θ + 4sin2θ = 0
⇒ -2(1 – sin2θ) + 4sin3θ + 4sin2θ = 0
⇒ -2 + 2sin2θ + 4sin3θ + 4sin2θ = 0
⇒ 2sin3θ + 3sin2θ – 1 = 0
⇒ (sin θ + 1)(2sin 2θ + sin θ – 1) = 0
⇒ sin θ = -1 or 2 sin 2θ + sinθ – 1 = 0
⇒ 2sin2θ + sin θ – 1 = 0 [∵sin θ ≠ -1, as 0 can’t be more than 90°]
⇒ (2sinθ – 1)(sin θ + 1) = 0
⇒ sin θ = \(\frac{1}{2}\) [∵sin θ ≠ -1]
∴θ = \(\frac{\pi}{6}\)

On differentiating both sides of Eq. (iii) w.r.t. 0, we get
P”(θ) = r(4cosec ² θ cotθ + 4sec ³ θ + 4secθtan ² θ + 8sec ² θtanθ)

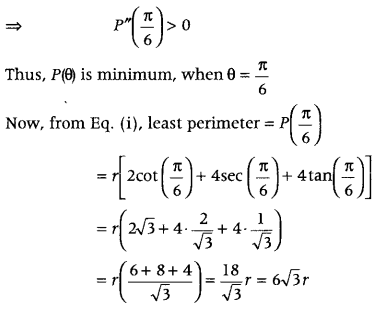
Hence Proved.

Question 14.
The sum of the surface areas of a cuboid with sides x, 2x and \(\frac{x}{3}\) and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of sphere. Also, find the minimum value of the sum of their volumes. (Foreign 2016)
Or
The sum of surface areas of a sphere and a cuboid with sides \(\frac{x}{3}\), x and 2x, is constant. Show that the sum of their volumes is minimum, if x is equal to three times the radius of sphere.
Answer:
Let r be the radius of the sphere and dimensions of cuboid are x, 2x and \(\frac{x}{3}\).

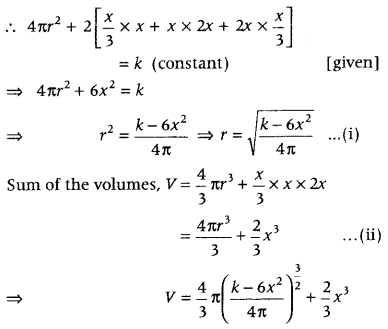
On differentiating both sides w.r.t. x, we get

Hence, V is minimum when x is equal to three times the radius of the sphere.
Hence proved.
Now, on putting r = \(\frac{x}{3}\) in Eq. (ii), we get

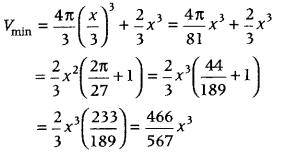
Question 15.
Find the local maxima and local minima of the function f(x) = sin x – cos x, 0 ≤ x ≤ 2π. Also, find the local maximum and local minimum values. (Delhi 2015)
Answer:
We have, f(x) = sin x – cos x, 0< x < 2π
On differentiating both sides w.r.t. x, we get
f'(x) = cosx + sinx ……….(i)
For local maximum and local minimum,
Put f'(x) = 0,
i.e. cosx + sinx = 0 ⇒ cosx = – sinx
⇒ tanx = -1 ⇒ x = π – \(\frac{\pi}{4}\) or 2π – \(\frac{\pi}{4}\)
⇒ x = \(\frac{3 \pi}{4}\) or \(\frac{7 \pi}{4}\)

Again, on differentiating both sides of Eq. (i) w.r.t. x, we get
f”(x) = – sin x + cos x

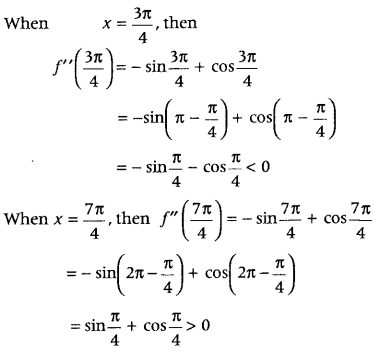
Thus, x = \(\frac{3 \pi}{4}\) is a point of local maxima and x = \(\frac{7 \pi}{4}\) is a point of local minima.

Now, the local maximum value

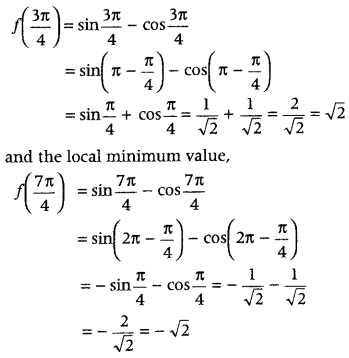
Question 16.
Find the minimum value of (ax + by), where xy = c ² . (Foreign 2015)
Answer:
let f(x) = ax + by, whose minimum value is required.

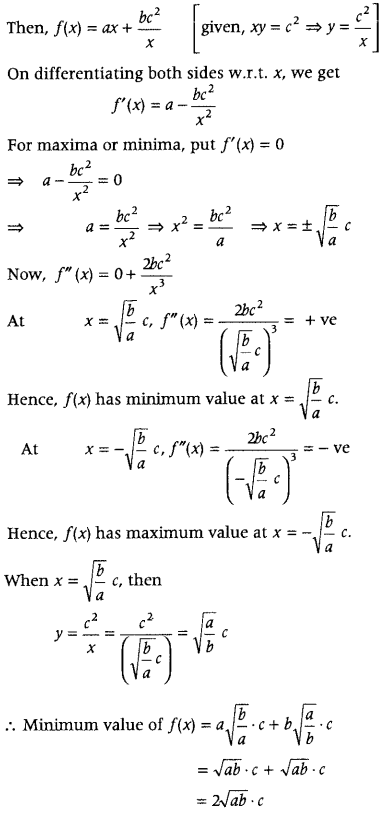
Question 17.
Find the coordinates of a point on the parabola y = x ² + 7x + 2 which is closest to the straight line y = 3x – 3. (Foreign 2015)
Answer:
Given equation of curve is y = x ² + 7x + 2 and equation of straight line is y = 3x – 3
Let P(x, y) be any point on the parabola y = x ² + 7x + 2.
Let D be the distance of point P from straight line, then

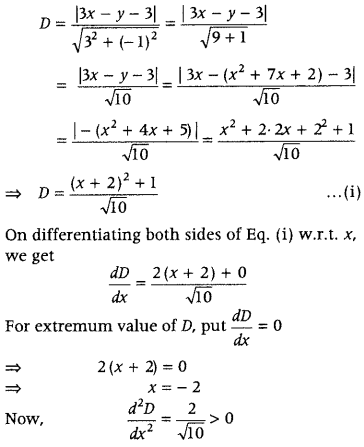
Thus, D is minimum when x = – 2
Now, y = x ² + 7x + 2 = (- 2) ² + 7 (-2) + 2
= 4 – 14 + 2 = -8
Hence, point (- 2, – 8) is on the parabola, which is closest to the given straight line.

Question 18.
A point on the hypotenuse of a right triangle is at distances a and b from the sides of the triangle. Show that the minimum length of the hypotenuse is (a ^2/3 + b ^2/3 ) ^3/2 . (Delhi 2015C)
Answer:
Let P be a point on the hypotenuse AC of right angled ΔABC.
Such that PL ⊥ AB and PL = a and PM ⊥ BC and PM = b.
Let ∠APL = ∠ACB = 6 [say]
Then, AP = a sec θ, PC = b cosec θ

Let l be the length of the hypotenuse, then
l = AP + PC
⇒ l = a sec θ + b cosec θ, 0 < θ< \(\frac{\pi}{2}\)

On differentiating both sides w.r.t. θ, we get
\(\frac{d l}{d \theta}\) = a sec θ tan θ – b cosec θ cot θ …(i)
For maxima or minima, put \(\frac{d l}{d \theta}\) = 0
⇒ a sec θ tan θ = b cosec θ cot θ
⇒ \(\frac{a \sin \theta}{\cos ^{2} \theta}=\frac{b \cos \theta}{\sin ^{2} \theta}\) ⇒ tan θ = \(\left(\frac{b}{a}\right)^{1 / 3}\)

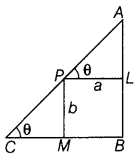
Again, on differentiating both sides of Eq. (i) w.r.t. θ, we get
\(\frac{d^{2} l}{d \theta^{2}}\) = a (sec θ × sec θ + tan θ × sec θ tan θ) – b [cosec θ (- cosec2 θ) + cot θ (- cosec θ cot θ)]
= a sec θ (sec2 θ + tan2 θ)+ b cosec θ (cosec θ + cot2 θ)

For 0 < θ < \(\frac{\pi}{2}\), all trigonometric ratios are positive. Also, a > 0 and b > 0

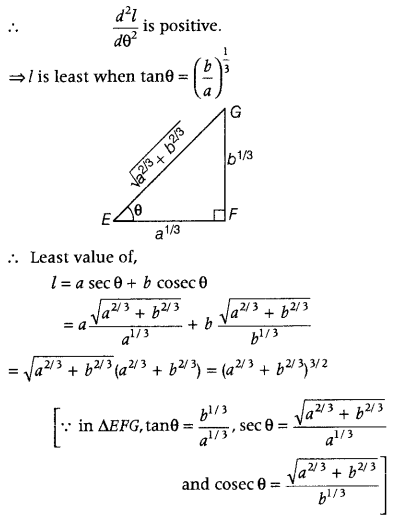
Hence Proved.

Question 19.
If the length of three sides of a trapezium other than the base are each equal to 10 cm, then find the area of the trapezium, when it is maximum. (All India 2014C, 2010; Delhi 2013C)
Answer:
Let ABCD be the given trapezium in which
AD = BC = CD =10cm.
AP = x cm
ΔAPD = ΔBQC
QB = x cm


⇒ -2(x ² + 5x – 5) = 0
⇒ -2(x + 1)(x – 5) = 0
x = 5 or -10
Since, x represents distance, so it cannot be negative.
Therefore, we take x = 5
On differentiating both sides of Eq. (ii) w.r.t. x, we get

Thus, area of trapezium is maximum at x = 5 and maximum arca is
A _max = (5 + 10)\(\sqrt{100-(5)^{2}}\) [put x = 5 in Eq. (i)]
= 15\(\sqrt{100-25}\) = 15\(\sqrt{75}\) = 75√3 cm ²

Question 20.
Find the point P on the curve y ² = 4ax, which is nearest to the point (11a, 0). (All India 2014C)
Answer:
Let P(x, y) be any point on y ² = 4ax.
Then, distance between (x, y) and (11a, 0) is given by

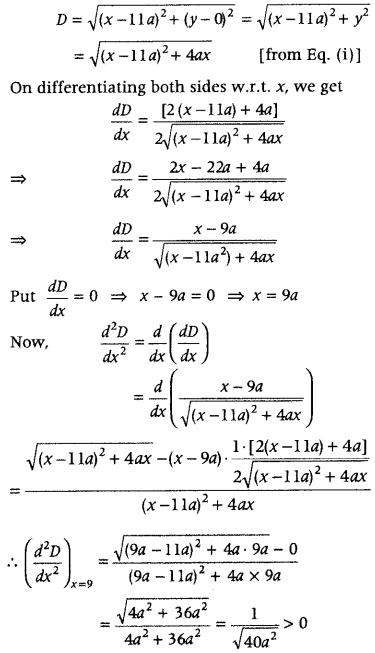
So, at (x = 9a), D is minimum.
Now, y ² = 36a ² ⇒ y = ± 6a
Hence, required points are (9a, 6a) and (9a, -6a).

Question 21.
Prove that the semi-vertical angle of the right circular cone of given volume and least curved surface area is cot ^-1 √2. (Delhi 2014)
Answer:
Let r be the radius of the base, h be the height, V be the volume, S be the surface area of the cone ABC and 0 be the semi-vertical angle.


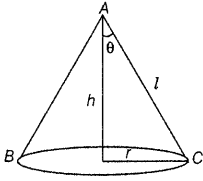
So, S ² or S is minimum, when
V ² = 2π ² r ⁶ /9

On putting V ² = 2π ² r ⁶ /9 in Eq. (i), we get
2π ² r ⁶ = π ² r ⁴ h ²
⇒ 2r ² = h ² ⇒ h = √2r ⇒ \(\frac{h}{r}\) = √2
⇒ cot θ = √2 [from the figure, cot θ = \(\frac{h}{r}\).]
∴ θ = cot ^-1 √2
Hence, the semi-vertical angle of the right circular cone of given volume and least curved surface area is cot ^-1 √2.
Hence proved.

Note: If square of any area is maximum (or minimum), then area is also maximum (or minimum).

Question 22.
Of all the closed right circular cylindrical cans of volume 128π cm ³ , find the dimensions of the can which has minimum surface area. (Delhi 2014)
Answer:
Let r cm be the radius of base and h cm be the height of the cylindrical can. Let its volume be V and S be its total surface area.


Thus, \(\frac{d^{2} S}{d r^{2}}\) > 0 at r = 4, so the surface area is dr ² minimum, when the radius of cylinder is 4 cm.
On putting the value of r in Eq. (i), we get
Hence, for the minimum surface area of can, the dimensions of the cylindrical can are r = 4 cm and h = 8 cm.

Question 23.
Show that a cylinder of a given volume which is open at the top has minimum total surface area, when its height is equal to the radius of its base. (Foreign 2014; Delhi 2011C)
Answer:
Let r be the radius, h be the height, V be the volume and S be the total surface area of a right circular cylinder which is open at the top.
Now, given that V = πr ² h
We know that, total surface area S is given by
S = 2πrh + πr ² [∵ cylinder is open at the top, therefore S = curved surface area of cylinder + area of base]

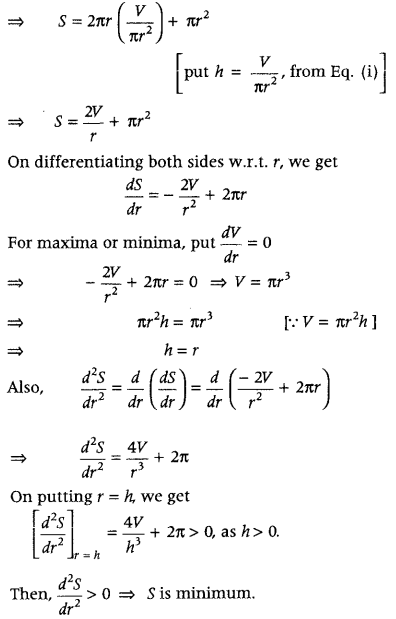
Hence, S is minimum, when h = r, i.e. when height of cylinder is equal to radius of the base.
Hence Proved.

Question 24.
Find the area of the greatest rectangle that can be inscribed in an ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1. (All India 2013)
Answer:
Let ABCD be a rectangle having area A inscribed in an ellipse \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 1 ………..(i)
Let the coordinates of A be (α, β).

Then, the coordinates of B = (α, -β)
C = (-α,-β)
D = (-α, β)
∴ Area of rectangle, A = Length × Breadth
= 2α × 2β ⇒ A = 4αβ

Question 25.
Show that the height of a closed right circular cylinder of given surface and maximum volume is equal to diameter of base. (Delhi 2012)
Answer:
Let S be the surface area, V be the volume, h be the height and r be the radius of base of the right circular cylinder.
We know that, Surface area of right circular cylinder,
S = πr ² + 2πrh ……(i)

= – 6πr < 0
∴ V is maximum
Hence, V is maximum at h = 2r
Hence Proved.

Question 26.
Prove that radius of right circular cylinder of greatest curved surface area which can be inscribed in a given cone is half of that of the cone. (All India 2012)
Answer:
Let VAB be the cone of base radius r, height h and radius of base of the inscribed cylinder be x.

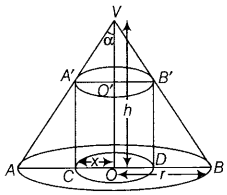
Now, we observe that

∴ C is maximum or greatest.
Hence, C is greatest at x = \(\frac{r}{2}\).
Hence proved.

Question 27.
An open box with a square base is to be made out of a given quantity of cardboard of area C ² sq units. Show that the maximum volume of box is \(\frac{C^{3}}{6 \sqrt{3}}\) cu units. (All India 2012)
Answer:
Let the dimensions of the box be x and y. Also, let V denotes its volume and S denotes its total surface area.
Now, S = x ² + 4xy [∵ S = area of square base + area of the four walls]
Given, x ² + 4xy = C ²

Hence, the maximum volume of box is \(\frac{C^{3}}{6 \sqrt{3}}\) cu units.
Hence Proved.

Question 28.
Prove that the area of a right angled triangle of given hypotenuse is maximum, when the triangle is isosceles. (Delhi 2012c)
Answer:
Let a and b be the sides of right angled triangle and c be the hypotenuse.

From ΔABC, we have
c ² = a ² + b ²

Hence, the triangle is isosceles.
Hence proved.

Question 29.
Show that the right circular cone of least curved surface and given volume has an altitude equal to √2 times the radius of the base. (Delhi 2011)
Answer:
Let C denotes the curved surface area, r be the radius of base, h be the height and V be the volume of right circular cone.
We know that, volume of cone is given by
V = \(\frac{1}{3}\)πr ² h ⇒ h = \(\frac{3 V}{\pi r^{2}}\) …(i)
Also, the curved surface area of cone is given by C = ml, where l = \(\sqrt{r^{2}+h^{2}}\) is the slant height of cone.
∴ C = πr\(\sqrt{r^{2}+h^{2}}\)

On squaring both sides, we get
C ² = π ² r ² (r ² + h ² )
⇒ C ² = π ² r ⁴ + π ² r ² h ²
Let C ² = Z
Then, Z = π ² r ⁴ + π ² r ² h ² ……….(ii)

⇒ Z is minimum ⇒ C is minimum.
Hence, curved surface area is least, when h = √2r.
Note: If C ² is maximum/minimum, then C is also maximum/minimum.

Question 30.
A window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, then find the dimensions of the rectangle that will produce the largest area of the window. (Delhi 2011)
Answer:
Let ABCD be the rectangle which is surmounted by an equilateral ΔEDC.

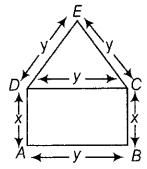
Now, given that Perimeter of window = 12 m
⇒ 2x + 2y + y = 12
∴ x = 6 – \(\frac{3}{2}\)y
Let A denotes the combined area of the window.
Then, A = area of rectangle + area of equilateral triangle

Hence, the area of the window is largest when the dimensions of the window are
x = \(\frac{18-6 \sqrt{3}}{6-\sqrt{3}}\) and y = \(\frac{12}{6-\sqrt{3}}\)

Question 31.
Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area. (All India 2011)
Answer:
Let ABCD be the rectangle which is inscribed in a fixed circle whose centre is 0 and radius b. Let AB = 2x and BC = 2y.

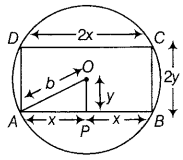
In right angled AOPA by Pythagoras theorem, we have
AP ² + OP ² = OA ²
x ² + y ² = b ²
y ² = b ² – x ²
⇒ y = \(\sqrt{b^{2}-x^{2}}\) …..(i)

Let A be the area of rectangle.
∴ A = (2x) (2y) [∵ area of rectangle = length x breadth]
⇒ A = 4 xy
⇒ A = 4x\(\sqrt{b^{2}-x^{2}}\) [∵ y = \(\sqrt{b^{2}-x^{2}}\)]

On differentiating both sides w.r.t. x, we get

Hence, area of rectangle is maximum, when 2x = 2y, i.e. when rectangle is a square.
Hence proved.

Question 32.
Show that of all the rectangles with a given perimeter, the square has the largest area. (Delhi 2011)
Answer:
Let x and y be the lengths of two sides of a rectangle. Again, let P denotes its perimeter and A be the area of rectangle.
Then, P = 2 (x + y) [∵ perimeter of rectangle = 2(l + b)]
⇒ P = 2x + 2y
⇒ y = \(\frac{P-2 x}{2}\) …..(i)

We know that, area of rectangle is given by
A = xy
⇒ A = x\(\left(\frac{P-2 x}{2}\right)\) [by using Eq. (i)]
⇒ A = \(\left(\frac{P-2 x}{2}\right)\)

On differentiating both sides w.r.t. x, we get
\(\frac{d A}{d x}=\frac{P-4 x}{2}\)

For maxima or minima, put \(\frac{d A}{d x}\) = 0
⇒ \(\frac{P-4 x}{2}\) = 0 ⇒ P = 4x
⇒ 2x + 2y = 4x [∵ P = 2x + 2y]
⇒ x = y

So, the rectangle is a square.
Also, \(\frac{d^{2} A}{d x^{2}}=\frac{d}{d x}\left(\frac{P-4 x}{2}\right)\)
= \(-\frac{4}{2}\) = -2 < 0
⇒ A is maximum.
Hence, area is maximum, when rectangle is a square.
Hence proved.

Question 33.
Show that of all the rectangles of given area, the square has the smallest perimeter. (Delhi 2011)
Answer:
Let x and y be the lengths of sides of a rectangle. Again, let A denotes its area and P be the perimeter.
Now, area of rectangle, A = xy

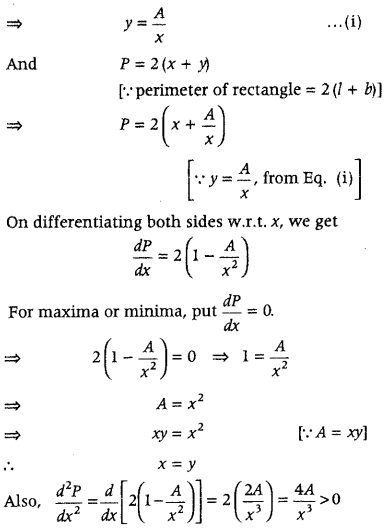
Here, x and A being the side and area of rectangle can never be negative. So, P is minimum.
Hence, perimeter of rectangle is minimum, when rectangle is a square.
Hence proved.

Question 34.
Show that the semi-vertical angle of a right circular cone of maximum volume and given slant height is tan ^-1 √2. (All India 2011)
Answer:
Let θ be the semi-vertical angle of the cone.
It is clear that θ ∈ (0, \(\frac{\pi}{2}\))
Let r, h and l be the radius, height and the slant height of the cone, respectively.

Since, slant height of the cone is given, so consider it as constant.
Now, in ΔABC, r = l sin θ and h = l cos θ
Let V be the volume of the cone.

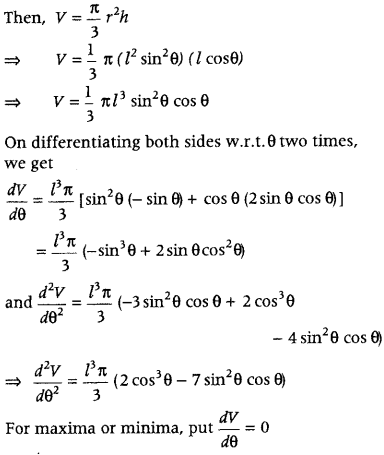
⇒ sin ³ θ = 2sinθ cos ² θ
⇒ tan ² θ = 2
⇒ tan θ = √2
⇒ θ = tan ^-1 √2

Now, when θ = tan ^-1 √2, then tan ² θ = 2
⇒ sin ² θ = 2cos ² θ

Now, we have

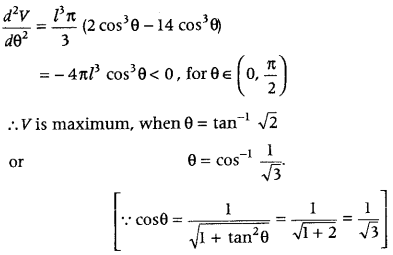
Hence, for given slant height, the semi-vertical angle of the cone of maximum volume is cos ^-1 \(\frac{1}{\sqrt{3}}\).

Question 35.
Find the point on the curve y ² = 2x which is at a minimum distance from the point (1, 4). (All India 2011)
Answer:
First, consider any point on the curve, use the, formula of distance between two points. Then, square both sides and eliminate one variable with i the help of given equation. Further, apply concept : of maxima and minima to find the required point.

The given equation of curve is y ² = 2x and the given point is Q (1,4).
Let P(x, y) be any point on the curve.
Now, distance between points P and Qis given by

Let PQ ² = Z
Then, Z = \(\frac{y^{4}}{4}\) – 8y + 17

On differentiating both sides w.r.t. y, we get
\(\frac{d Z}{d y}=\frac{4 y^{3}}{4}\) – 8 = y ³ – 8

For maxima or minima, put \(\frac{d Z}{d y}\) = 0
⇒ y ³ – 8 = 0 ⇒ y ³ = 8
⇒ y = 2
Also, \(\frac{d^{2} Z}{d y^{2}}=\frac{d}{d y}\)(y ³ – 8) = 3y ²

On putting y = 2, we get
\(\left(\frac{d^{2} Z}{d y^{2}}\right)_{y=2}\) = 3(2) ² = 12 >0
\(\frac{d^{2} Z}{d y^{2}}\) > 0

∴ Z is minimum and therefore PQ is also minimum as Z = PQ ² .
On putting y = 2 in the given equation, i.e. y ² = 2x, we get
(2) ² = 2x
⇒ 4 = 2x
⇒ x = 2
Hence, the point which is at a minimum distance from point (1, 4) is P (2, 2).

Question 36.
A wire of length 28 m is to be cut into two pieces. One of the two pieces is to be made into a square and the other into a circle. What should be the lengths of two pieces, so that the combined area of circle and square is minimum? (All India 2010)
Answer:
First, find length of circular part (or its circumference) and calculate the length of square part (or its perimeter). Add these two terms and equate it to 28 m and apply second derivative test to check minimum.

Let x m be the side of the square and r be the radius of circular part. Then,
Length of square part = perimeter of square = 4 × Side = 4 × and length of circular part
= circumference of circle = 2πr
Given, length of wire = 28 ⇒ 4x + 2πr = 28
⇒ 2x + πr = 14
∴ x = \(\frac{14-\pi r}{2}\) ……(i)

Let A denotes the combined area of circle and square.
Then, A = πr ² + x ²

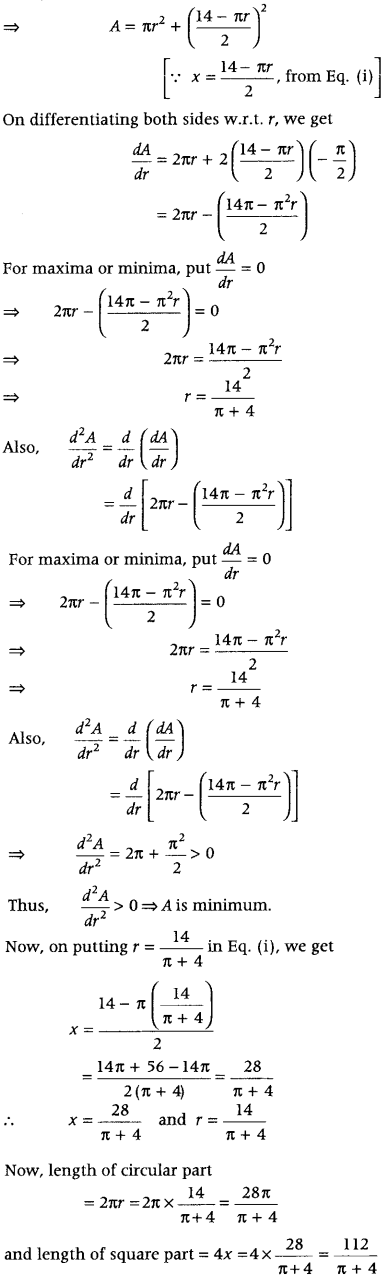
which are the required length of two pieces.

Question 37.
Show that the volume of the largest cone that can be inscribed in a sphere of radius R is \(\frac{8}{27}\) of the volume of the sphere. (Delhi 2010C)
Answer:
Let R be the radius and h be the height of the cone, which inscribed in a sphere of radius r.
∴ OA = h – r

In ΔOAB, by Pythagoras theorem, we have
r ² = R ² + (h – r) ²
⇒ r = R ² + h ² + r ² – 2rh
⇒ R ² = 2rh – h ² ……….(i)

The volume of sphere = \(\frac{4}{3}\) πr ³

and the volume V of the cone,
V = \(\frac{1}{2}\) πR ² h
⇒ V = \(\frac{1}{2}\) πh (2rh – h ² ) [from Eq. (i)]
⇒ V = \(\frac{1}{2}\) π (2rh ² – h ³ ) …..(ii)

On differentiating both sides of Eq, (ii) w.r.t. h, we get

⇒ V is maximum at h = \(\frac{4r}{3}\).
Hence proved.

On substituting the value of h in Eq. (ii), we get

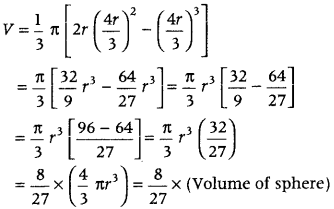
Hence, maximum volume of the cone is \(\frac{8}{27}\) of the volume of the sphere.

Question 38.
Find the maximum area of an isosceles triangle inscribed in the ellipse \(\frac{x^{2}}{25}+\frac{y^{2}}{16}\) = 1, with its vertex at one end of the major axis. (Delhi 2010c)
Answer:
Given equation of ellipse is
\(\frac{x^{2}}{25}+\frac{y^{2}}{16}\) = 1

Here, a = 5, b = 4 a > b
So, major axis is along X-axis.
Let ABTC be the isosceles triangle which is inscribed in the ellipse and OD = x, BC = 2y and TD = 5 – x.

Let A denotes the area of triangle. Then, we have
A = \(\frac{1}{2}\) × base × height = \(\frac{1}{2}\) × BC × TD
⇒ A = \(\frac{1}{2}\) .2y (5 – x) ⇒ A = y (5 – x)

On squaring both sides, we get
A ² = y ² (5 – x) ² …….(i)

For maxima or mmima, put \(\frac{d Z}{d x}\) = 0
⇒ \(-\frac{32}{25}\) (5 – x) ² (2x + 5) = 0 ⇒ x = 5 or –\(\frac{5}{2}\)
Now, when x = 5, then
Z = \(\frac{16}{25}\) (25 – 25)(5 – 5) ² = 0
which is not possible.
So, x = 5 is rejected.

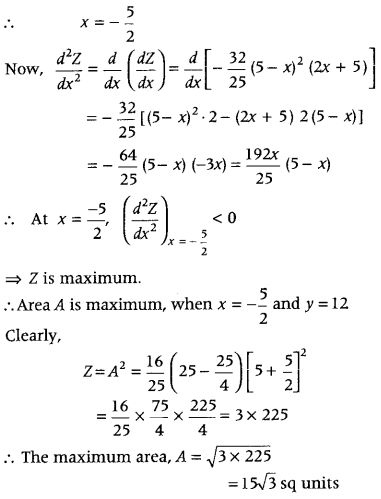
Note: If A ² is maximum/minimum, then A is also maximum/minimum.

Question 39.
Show that the right circular cylinder, open at the top and of given surface area and maximum volume is such that its height is equal to the radius of the base. (Delhi 2010)
Answer:
Let V be the volume, S be the total surface area of a right circular cylinder which is open at the top. Again, let r be the radius of base and h be the height.
Now, S = 2πrh + πr ² [∵ cylinder is open at top]
⇒ h = \(\frac{S-\pi r^{2}}{2 \pi r}\) ……….(i)

Also, volume of cylinder is given by
V = πr ² h

Hence, volume of cylinder is maximum, when its height is equal to radius of the base.
Hence proved.