Continuity and Differentiability Class 12 Maths Important Questions Chapter 5

Get access to Class 12 Maths Important Questions Chapter 5 Continuity and Differentiability, Continuity and Differentiability Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.

Continuity and Differentiability Class 12 Important Questions with Solutions Previous Year Questions

Continuity

Question 1.
Determine the value of ‘k’ for which the following function is continuous at x = 3: (All India 2017)

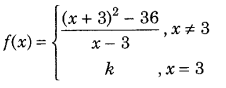
Answer:

Question 2.
Determine the value of the constant ‘k’ so that the function

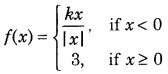
is continuous at x = 0. (Delhi 2017)
Answer:

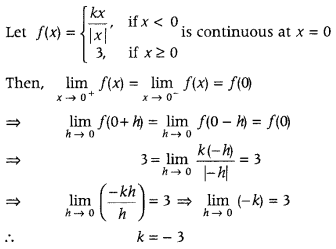
Question 3
Find the values of p and q for which

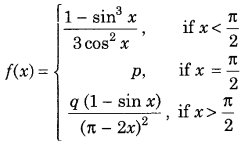
is continuous at x = \(\frac{\pi}{2}\). (Delhi 2016)
Answer:

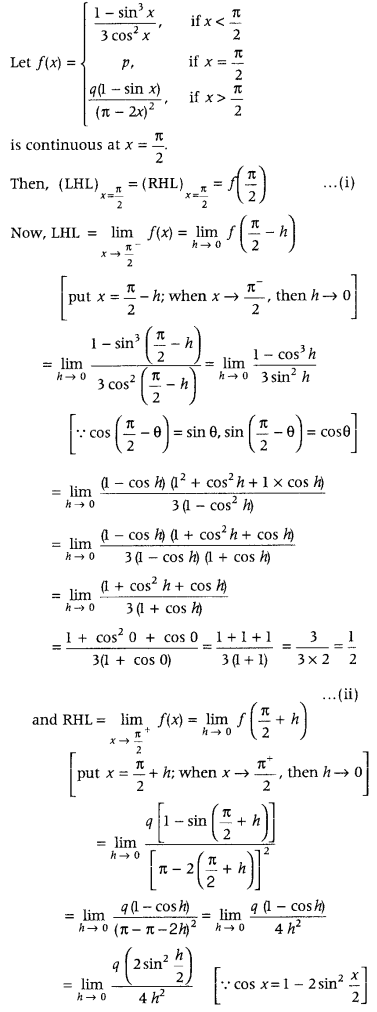
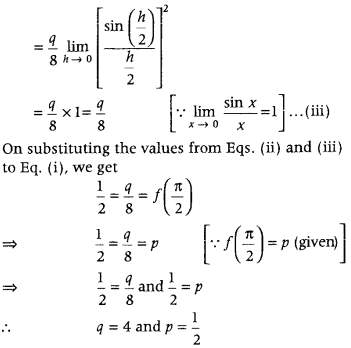
Question 4.
If

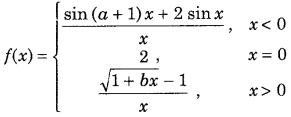
is continuous at x = 0, then find the values of a and b. (All India 2015)
Answer:

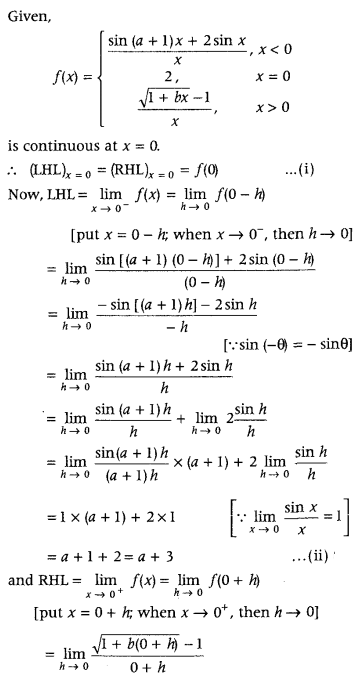
Question 5.
Find the value of k, so that the function

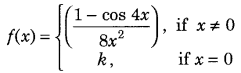
is continuous at x = 0. (All India 2014C).

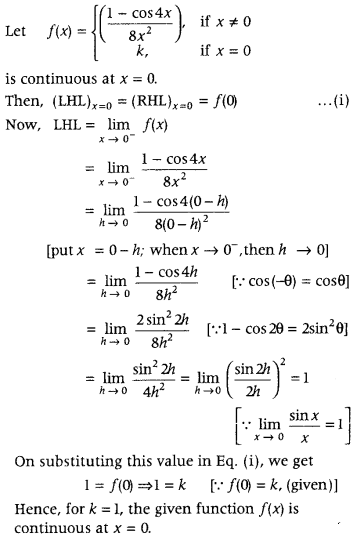
Alternate Method:

Question 6.
If

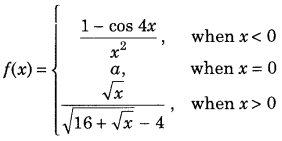
and f is continuous at x = 0, then find the value of a. (Delhi 2013C)
Answer:

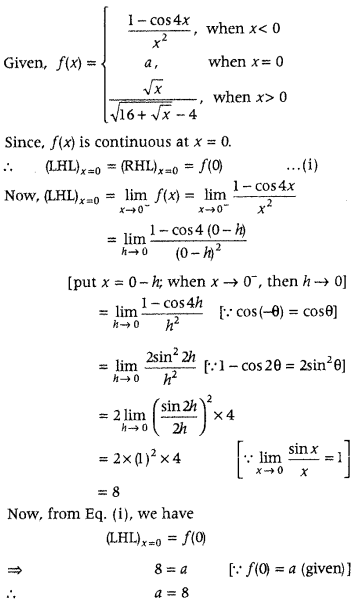
Question 7.
Find the value of k, for which

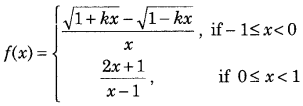
is continuous at x = 0. (All India 2013)
Answer:

Question 8.
Find the value of k, so that the following function is continuous at x = 2. (Delhi 2012C)

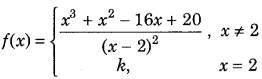
Answer:

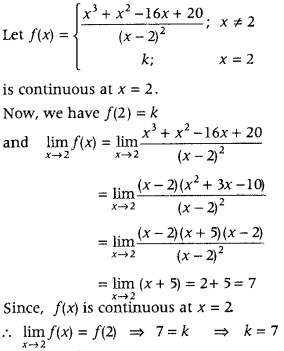
Question 9.
Find the value of k, so that the function f defined by

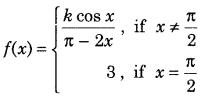
is continuous at x = \(\frac{\pi}{2}\). (Delhi 2012C; Foregin 2011)
Answer:

Question 10.
Find the value of a for which the function f is defined as

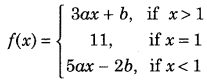
is continuous at x = 0. (Delhi 2011)
Answer:

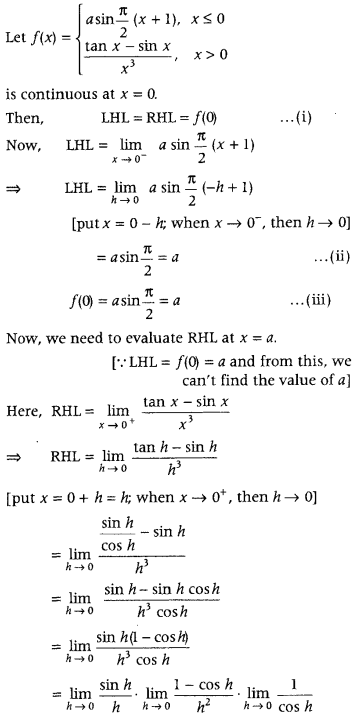
Question 11.
If the function f(x) given by

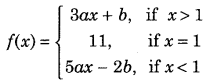
is continuous at x = 1, then find the values of a and b. (Delhi 2011; All India 2010)
Answer:

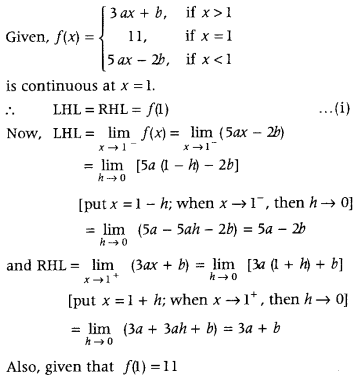
On substituting these values in Eq. (i), we get
5a – 2b = 3a + b = 11
⇒ 3a + b = 11 …… (ii)
and 5a – 2b = 11 ……. (iii)
On subtracting 3 × Eq. (iii) from 5 × Eq. (ii), we get
15a + 5b – 15a + 6b = 55 – 33
⇒ 11b = 22 ⇒ b = 2
On putting the value of b in Eq. (ii). we get
3a + 2 = 11 ⇒ 3a = 9 = a = 3
Hence, a = 3 and b = 2

Question 12.
Find the values of a and b such that the following function f(x) is a continuous function. (Delhi 2011)

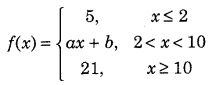
Answer:

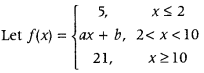
is a continuous function. So, it is continuous at x = 2 and at x = 10.
∴ By definition.
(LHL) _x=2 = (RHL) _x=2 = f(2) …… (i)
and (LHL) _x=10 = (RHL) _x=10 = f(10) …… (ii)
Now, let us calculate LHL and RHL at x = 2.

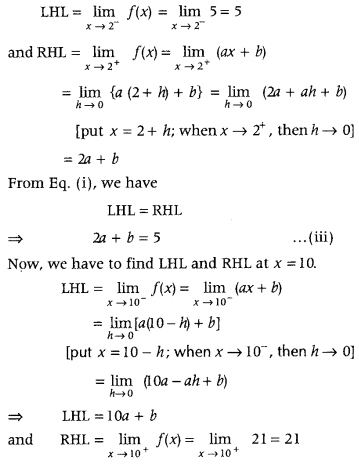
Now, from Eq. (ii), we have
LHL= RHL
⇒ 10a + b = 21 ….. (iv)
On subtracting Eq. (iv) from Eq. (iii), we get
– 8a = – 16
⇒ a = 2
On putting a = 2 in Eq. (iv), we get
2a + b = 21 ⇒ b = 1
Hence, a = 2 and b = 1

Question 13.
Find the relationship between a and b, so that the function f defined by

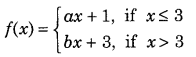
is continuous at x = 3. (All India 2011)
Answer:
let

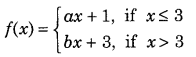
is a continuous at x = 3.
Then, LHL = RHL = f(3) ……. (i)

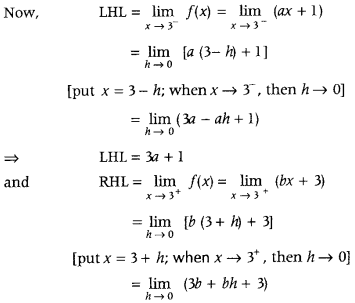
⇒ RHL = 3b + 3
From Eq.(i), we have
LHL = RHL ⇒ 3a + 1 = 3b + 3
Then, 3a – 3b = 2, which is the required relation between a and b.

Question 14.
Find the value of k, so that the function f defined by

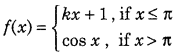
is continuous at x = π. (Foreign 2011)
Answer:

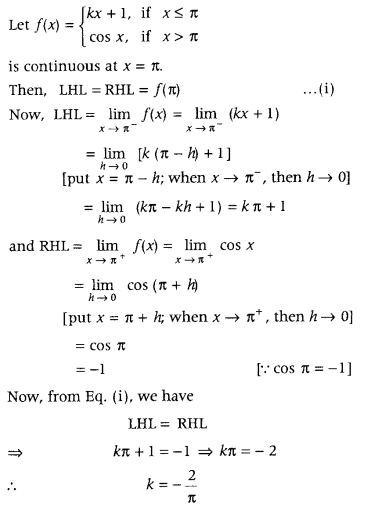
Question 15.
For what values of λ, is the function

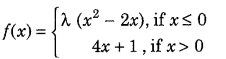
is continuous at x = 0? (Foreign 2011)
Answer:

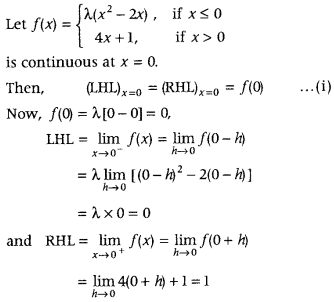
∵ LHL ≠ RHL, which is a contradiction to Eq. (i).
∴ There is no value of λ. for which f(x) is continuous at x = 0.

Question 16.
Discuss the continuity of the function f(x) at x = 1/2 , when f(x) is defined as follows. (Delhi 2011C)

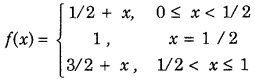
Answer:
Here, we find LHL, RHL and f\(\left(\frac{1}{2}\right)\).
If LHL = RHL = f\(\left(\frac{1}{2}\right)\) then we say that f(x) is continuous at x = \(\frac{1}{2}\), otherwise f(x) discontinuous at x = \(\frac{1}{2}\).

Given function is

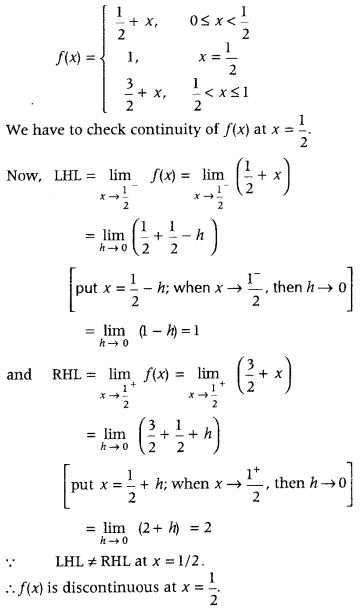
Question 17.
Find the value of α, if the function f(x) defined by

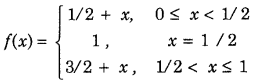
is continuous at x = 2. Also, discuss the continuity of f(x) at x = 3. (All India 2011C)
Answer:

Question 18.
Find the values of a and b such that the function defined as follows is continuous. (Delhi 2010, 2010C)

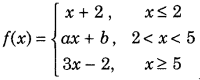
Answer:
a = 3 and b = – 2

Question 19.
For what value of k, is the function defined by

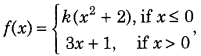
continuous at x = 0?
Also, find whether the function is continuous at x = 1. (Delhi 2010, 2010C)
Answer:

Question 20.
Find all points of discontinuity of f, where f is defined as follows.

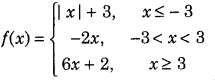
Answer:
First, verify continuity of the given function at x = – 3 and x = 3. Then, point at which the given function is discontinuous will be the point of discontinuity.

⇒ RHL = 6
Also, f(- 3) = value of f(x) at x = – 3
= – (- 3) + 3
= 3 + 3 = 6
∵ LHL = RHL f(- 3)
∴ f(x) is continuous at x = – 3 So, x = – 3 is the point of continuity.

Continuity at x = 3

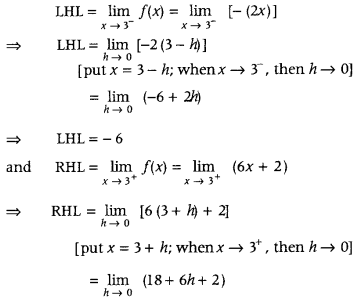
⇒ RHL = 20
∵ LHL ≠ RHL
∴ f is discontinuous at x = 3
Now, as f (x) is a polynomial function for x < – 3, – 3 < x < 3 and x > 3, so it is continuous in these intervals.
Hence, only x = 3is the point of discontinuity of f(x).

Differentiability

Question 1.
Differentiate \(e^{\sqrt{3 x}}\), with respect to x. (All India 2019)
Answer:
Let y = \(e^{\sqrt{3 x}}\)

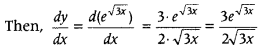
Question 2.
If y = cos (√3x), then find \(\frac{d y}{d x}\). (All India 2019)
Answer:
Given, y = cos (√3x)
Differentiating w.r.t x, we get

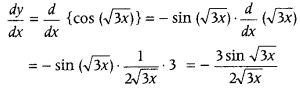
Question 3.
If f(x) = x + 1, find \(\frac{d}{d x}\) (fof) (x). (Delhi 2019)
Answer:
Given, f(x) = x + 1
⇒ f(f(x)) = f(x) + 1
⇒ fof(x) = x + 1 + 1
⇒ fof(x) = x + 2
Now, \(\frac{d}{d x}\) (fof)(x) = \(\frac{d}{d x}\)(x + 2) = 1

Question 4.
If f(x) = x + 7 and g(x) = x – 7, x ∈ R, then find the values of \(\frac{d}{d x}\) (fog) x. (Delhi 2019)
Answer:
Given, f(x) = x + 7,
g(x) = x – 7, x ∈ R
Now, (fog) (x) = f[g(x)] = f(x – 7) = (x – 7) + 7
(fog) (x) = x
On differentiate w.r.t. x, we get
\(\frac{d}{d x}\) (fog)(x) = \(\frac{d}{d x}\) (x) ⇒ \(\frac{d}{d x}\) (fog) (x) = 1

Question 5.
If y = x|x|, find \(\frac{d y}{d x}\) for x < 0. (All India 2019)
Answer:
We have, y = x|x|
When, x < 0, then |x| = – x
∴ y = x(- x) = – x ²
⇒ \(\frac{d y}{d x}\) = – 2x

Question 6.
Differentiate tan ^-1 \(\left(\frac{1+\cos x}{\sin x}\right)\) with respect to x. (CBSE 2018)
Answer:

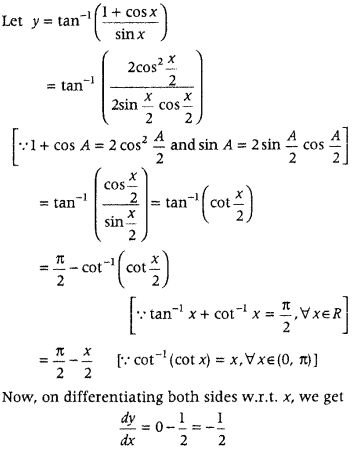
Question 7.
Differentiate tan ^-1 \(\left(\frac{\cos x-\sin x}{\cos x+\sin x}\right)\) with respect to x. (CBSE 2018 C)
Answer:

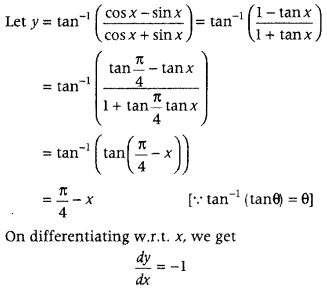
Question 8.
Find the value of c in Rolle’s theorem for the function f(x) = x ³ – 3x in [-√3, 0]. (All India 2017)
Answer:
Given, f(x) = x ³ – 3x in [-√3, 0]
We know that, according to Rolles theorem, if f(x) is continuous in [a, b] differentiable in (a, b) and f(a) = f(b), then there exist c ∈ (a, b) such that f’(c) = 0.
Here f(x), being a polynomial function, is continuous in [-√3, 0] and differentiable in (-√3, 0).
Also, f(-√3) = 0 = f(0)
∴ f'(c) = 0, for some c ∈ (- √3, 0) …… (ii)
Now, f’(x) = 3x ² – 3 [from Eq. (i)]
⇒ f’(c) = 3c ² – 3 = 0 [from Eq. (ii)]
⇒ c = ± 1
But C ∈ (-√3, 0) so neglecting positive value of c.
∴ c = – 1

Question 9.
Find \(\frac{d y}{d x}\) at x = 1, y = \(\frac{\pi}{4}\) if sin ² y + cos xy = K. (Delhi 2017)
Answer:
we have sin ² y + cos xy = k
On differentiating both sides w.r.t x, we get

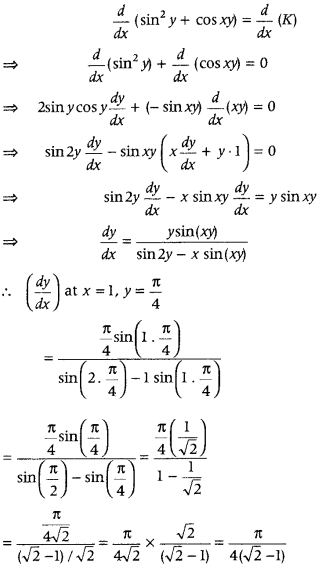
Question 10.
If y = sin ^-1 (6x\(\sqrt{1-9 x^{2}}\)), < \(\frac{1}{3 \sqrt{2}}\) x < \(\frac{1}{3 \sqrt{2}}\) then find \(\frac{d y}{d x}\). (Delhi 2017)
Answer:
Given, y = sin ^-1 (6x \(\sqrt{\left.1-9 x^{2}\right)}\))
y = sin ^-1 (2.3x \(\sqrt{1-(3 x)^{2}}\))
put 3x = sin θ, then
y = sin ^-1 (2 sin θ\(\sqrt{1-\sin ^{2} \theta}\))
⇒ y = sin ^-1 (2 sin θ. cos θ)
⇒ y = sin ^-1 (sin 2θ)
⇒ y = 2θ
⇒ y = 2 sin ^-1 (3x) [∵ θ = sin ^-1 (3x)]
⇒ \(\frac{d y}{d x}=\frac{2}{\sqrt{1-9 x^{2}}}\)
⇒ \(\frac{d y}{d x}=\frac{6}{\sqrt{1-9 x^{2}}}\)

Question 11.
If (cos x) ^y = (cos y) ^x , then find \(\frac{d y}{d x}\). (All India 2019; Delhi 2012)
Answer:
First, take log on both sides, then differentiate both sides by using product rule.
Given, (cos x) ^y = (cos y) ^x
On taking log both sides, we get
log (cos x) ^y = log (cos y) ^x
⇒ y log (cos x) = x log(cos y)
[∵ log x ⁿ = n log x]
On differentiating both sides w.r.t. x, we get

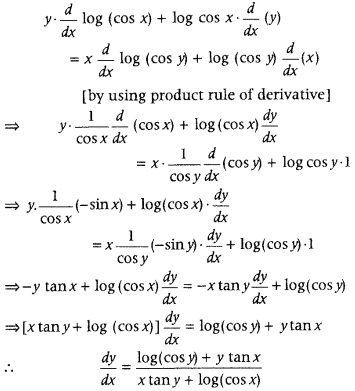
Question 12.
If \(\sqrt{1+y}+y \sqrt{1+x}=0\) = 0,(x ≠ y), then prove that \(\frac{d y}{d x}=-\frac{1}{(1+x)^{2}}\). (All India 2019: Foreign 2012; Delhi 2011C)
Answer:
First, solve the given equation and convert it into y = f(x) form. Then, differentiate to get the required result.
To prove \(\frac{d y}{d x}=-\frac{1}{(1+x)^{2}}\)
Given equation is \(\sqrt{1+y}+y \sqrt{1+x}\) = 0,
where x ≠ y, we first convert the given equation into y = f(x) form.
Clearly, x \(\sqrt{1+y}\) = – y \(\sqrt{1+x}\)
On squaring both sides, we get
⇒ x ² (1 + y) = y ² (1 + x)
⇒ x ² + x ² y = y ² + y ² x
⇒ x ² – y ² = y ² x – x ² y
⇒ (x – y) (x + y) = – xy (x – y)
[∵ a ² – b ² = (a – b) (a + b)]
⇒ (x – y) (x + y) + xy (x – y) = 0
⇒ (x – y) (x + y + xy) = 0
∴ Either x – y = 0 or x + y + xy = 0
Now, x – y = 0 ⇒ x = y
But it is given that x ≠ y.
So, it is a contradiction.
∴ x – y = 0 is rejected.
Now, consider y + xy + x = 0
⇒ y(1 + x) = – x ⇒ y = \(\frac{-x}{1+x}\)
On differentiating both sides w.r.t. x, we get

Question 13.
If y = (sin ^-1 x) ² prove that
(1 – x ² )\(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) – 2 = 0 (Delhi 2019)
Answer:
Given y = (sin ^-1 x) ²
Differentiating on w.r.t x, we get

Question 14.
If (x – a) ² + (y – b) ² = c ² , for some c > 0,
prove that

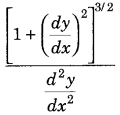
independent of a and b. (All India 2019)
Answer:
Given (x – a) ² + (y – b) ² = c ²
Differentiating on w.r.t x, we get

Question 15.
If x = ae ^t (sin t + cos t) and y = ae ^t (sin t – cos t), then prove that \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (All India 2019)
Answer:
Given x = x = ae ^t (sin t + cos t)
and y = ae ^t (sin t – cos t)

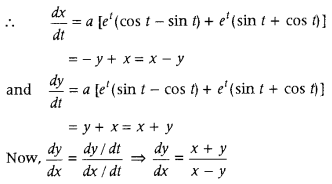
Question 16.
Differentiate x ^{sin x} + (sin x) ^{cos x} with respect to x. (All IndIa 2019)
Answer:

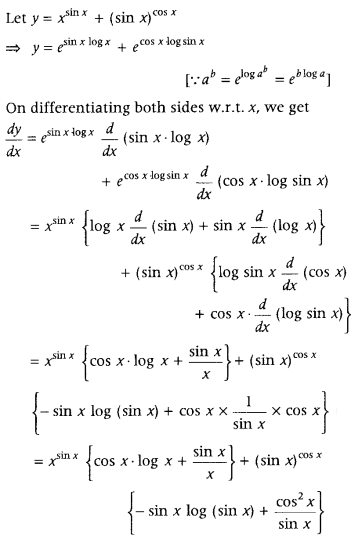
Question 17.
If log (x ² + y ² ) = 2 tan ^-1 \(\left(\frac{y}{x}\right)\) show that \(\frac{d y}{d x}=\frac{x+y}{x-y}\) (Delhi 2019)
Answer:
log (x ² + y ² ) = 2 tan ^-1 \(\left(\frac{y}{x}\right)\)
on differentiating both sides w.r.t. x, we get

Question 18.
If x ^y – y ^x = ab, find \(\frac{d y}{d x}\). (Delhi 2019)
Answer:

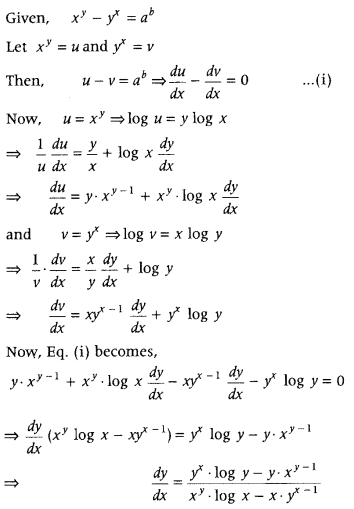
Question 19.
If x = cos t + log tan\(\left(\frac{t}{2}\right)\), y = sin t, then find the values of \(\frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\) at t = \(\frac{\pi}{4}\). (Delhi 2019; All IndIa 2012 C)
Answer:

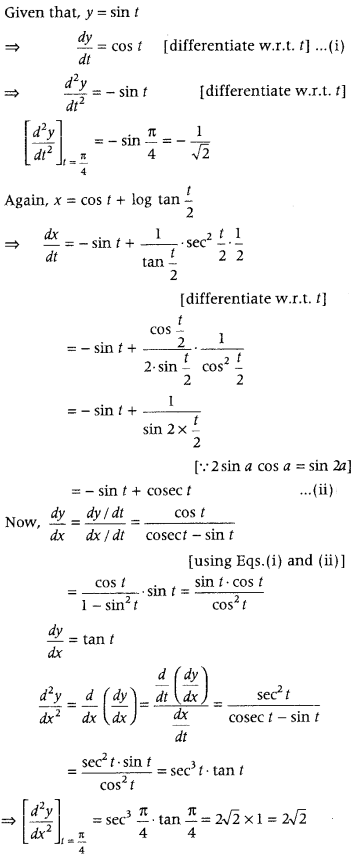
Question 20.
If y = sin (sin x), prove that
\(\frac{d^{2} y}{d x^{2}}\) + tan x \(\frac{d y}{d x}\) + y cos x = 0. (CBSE 2018)
Answer:
Given y = sin (sin x) ….. (i)
On differentiating both sides w.r.t. x we get
\(\frac{d y}{d x}\) = cos (sin x) . cos x ….. (ii)
Again. on differentiating both sides w.r.t. z.
we get
\(\frac{d^{2} y}{d x^{2}}\) = cos (sin x) . (- sin x) + cos x (- sin (sin x)) . cos x

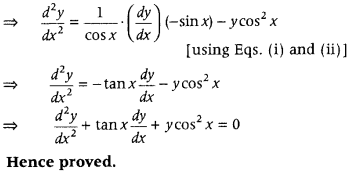
Question 21.
If (x ² + y ² ) ² = xy, find \(\frac{d y}{d x}\). (CBSE 2018)
Answer:
We have (x ² + y ² ) ² = xy
on differentiating both sides w.r.t. x, we get

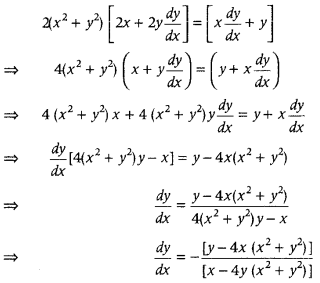
Question 22.
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ), find \(\frac{d y}{d x}\) when θ = \(\frac{\pi}{3}\). (CBSE 2018)
Answer:

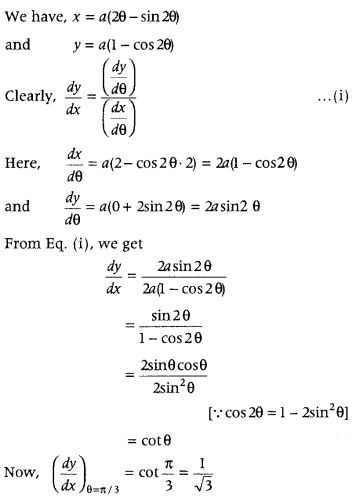
Question 23.
If sin y = x cos(a + y), then show that
\(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\cos a}\).
Also, show that \(\frac{d y}{d x}\) = cos a, when x = 0. (CBSE 2018 C)
Answer:

Question 24.
If x = a sec ³ θ and y = a tan ³ θ, find \(\frac{d^{2} y}{d x^{2}}\) at θ = \(\frac{\pi}{3}\). (CBSE 2018C)
Answer:

Question 25.
If y = e ^{tan -1} x, prove that (1 + x ² )\(\frac{d^{2} y}{d x^{2}}\) + (2x – 1)\(\frac{d y}{d x}\) = 0. (CBSE 2018 C)
Answer:
we have, y = e ^{tan -1} x
on differentiating both sides w.r.t. x, we get

Question 26.
If x ^y + y ^x = a ^b , then find \(\frac{d y}{d x}\). (All India 2017)
Answer:
\(\frac{d y}{d x}\) = \(\frac{-x^{y-1} \cdot y-y^{x} \log y}{x^{y} \log x+y^{x-1} \cdot x}\)

Question 27.
If e ^y (x + 1) = 1, then show that \(\frac{d^{2} y}{d x^{2}}=\left(\frac{d y}{d x}\right)^{2}\). (All India 2017)
Answer:
Given, e ^y (x + 1) = 1
On taking log both sides, we get
log [e ^y (x + 1) = log]
y + log(x + 1) = log 1 [∵ log e ^y = y]
On differentiating both sides w.r.t x, we get
\(\frac{d y}{d x}+\frac{1}{x+1}\) = 0 …… (i)
Again, differentiating both sides w.r.t. ‘x’, we get

Question 28.
If y = x ^x , then prove that (Delhi 2016, 2014)
\(\frac{d^{2} y}{d x^{2}}-\frac{1}{y}\left(\frac{d y}{d x}\right)^{2}-\frac{y}{x}\) = 0 (Delhi 2016, 2014)
Answer:
Given y = x ^x
On taking log both sides, we get
log y = log x ^x
⇒ log y = x log x
On differentiating both sides w.r.t x, we get

Question 29.
Differentiate tan ^-1 \(\left(\frac{\sqrt{1+x^{2}}-1}{x}\right)\) w.r.t. sin ^-1 \(\left(\frac{2 x}{1+x^{2}}\right)\), when x ≠ 0. (Delhi 2016, 2014)
Answer:

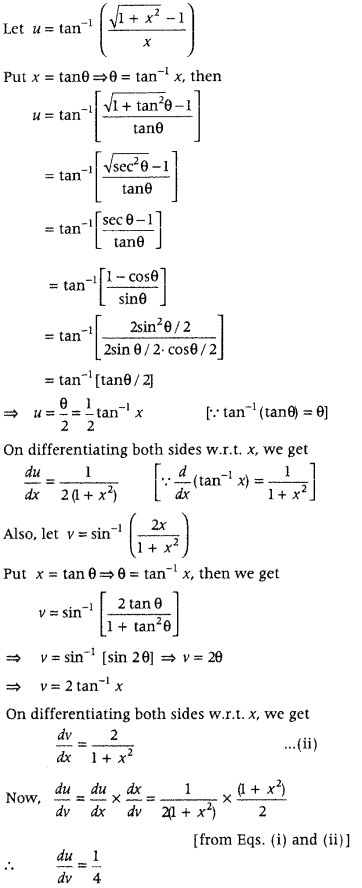
Question 30.
If x = a sin 2t(1 + cos 2t)and
y = b cos 2t (1 – cos 2t), then find the values of \(\frac{d y}{d x}\) at t = \(\frac{\pi}{4}\) and t = \(\frac{\pi}{3}\). (Delhi 2016; All India 2014)
Or
If x = a sin2t(1 + cos 2t) and y = b cos 2t (1 – cos 2t), then show that at t = \(\frac{\pi}{4}, \frac{d y}{d x}=\frac{b}{a}\) (All India 2014).
Answer:
Given, x = a sin 21(1 + cos 2t)
and y = b cos 2t(1 – cos 2t)
On differentiating x and y separately w.r.t. t,
we get
\(\frac{d x}{d t}\) = a[sin 2t \(\frac{d}{d t}\)(1 + cos 2t) + (1 + cos 2t) \(\frac{d}{d t}\) (sin 2t)
[by using product rule of derivative]
= a [sin2t × (0 – 2 sin 2t) + (1 + cos 2t) (2 cos 2t)]
= a (- 2 sin ² 2t + 2 cos 2t + 2 cos ² 2t)
= a[2(cos ² 2t – sin ² 2t) + 2 cos 2t]
= a (2 cos 4t + 2 cos 2t) = 2a (cos 4t + cos 2t)
[∵ cos ² 2θ – sin ² 2θ = cos 4θ]

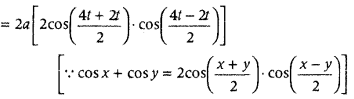
= 4a cos 3t cos t
and \(\frac{d y}{d t}\) = b[cos 2t \(\frac{d}{d t}\) (1 – cos 2t) + (1 – cos2t) \(\frac{d}{d t}\) (cos 2t)]
[by using product rule of derivative]
= b [cos 2t × (0 + 2 sin 2t) + (1 – cos 2t) (- 2 sin 2t)]
= b (2 sin 2t cos 2t – 2 sin 2t + 2 sin 2 t cos 2t)
= 2b (2 sin 2t cos 2t – sin 2t)
= 2b (sin 4 t – sin 2 t) [∵ 2 sin 2θ cos 2θ = sin 4θ]

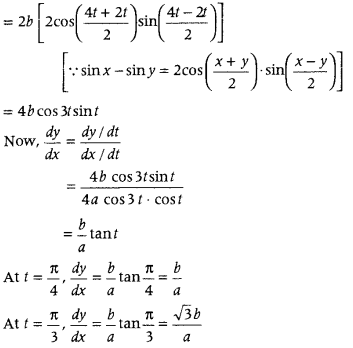
Question 31.
If x cos(a + y) = cos y, then prove that \(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\). Hence, show that sin α \(\frac{d^{2} y}{d x^{2}}\) + sin 2 (α + y) \(\frac{d y}{d x}\) = 0. (All India 2015).
Or
If cos y = x cos(α + y), where cos α ≠ ±1, prove that \(\frac{d y}{d x}=\frac{\cos ^{2}(a+y)}{\sin a}\). (Foregin 2014).
Answer:

Question 32.
Find \(\frac{d y}{d x}\), if y = sin ^-1 \(\left[\frac{6 x-4 \sqrt{1-4 x^{2}}}{5}\right]\) (All IndIa 2016).
Answer:

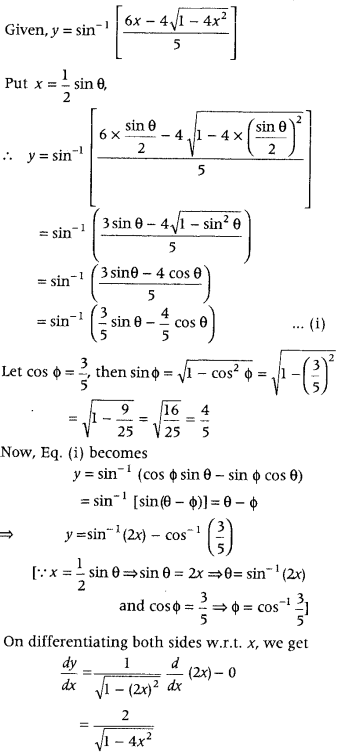
Question 33.
Find the values of a and b, if the function f defined by

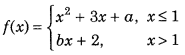
is differentiable at x = 1. (Foreign 2016)
Answer:

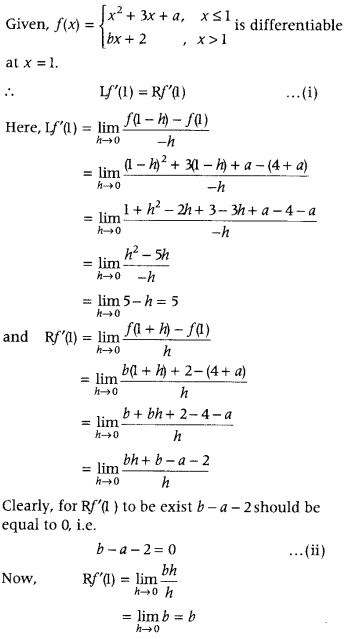
From Eq. (i), we have
Lf'(1) = Rf'(1)
⇒ 5 = b
⇒ b = 5
Now, on substituting b = 5 in Eq. (ii), we get
5 – a – 2 = 0
⇒ a = 3
Hence, a = 3 and b = 5.

Question 34.
If x = sin t and y = sin pt, then prove that
(1 – x ² )\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) + p ² y = 0. (Foreign 2015)
Answer:
Given, x = sin t and y = sin pt
On differentiating x and y separately w.r.t t, we get

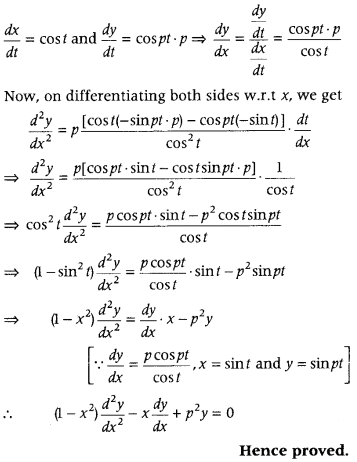
Question 35
If y = tan ^-1 \(\left(\frac{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}{\sqrt{1+x^{2}}-\sqrt{1-x^{2}}}\right)\), x ² ≤ 1, then find dy/ dx. (Delhi 2015)
Answer:
First, put x ² = sin θ, then reduce it in simplest form.
Further, differentiate it.

Question 36.
If x = a cos θ + b sin θ, y = a sin θ – b cos θ, then show that y ² \(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) + y = 0. (Delhi 2015. ForeIgn 2014 )
Answer:
Given x = a cos θ + b sin θ, ……. (i)
and y = a sin θ – b cos θ …….. (ii)
On differentiating both sides of Eqs. (i) and (ii) w.r.t. θ, we get

Question 37.
Show that the function f(x) = |x + 1| + |x – il, for all x ∈ R, is not differentiable at the points x = – 1 and x = 1. (All India 2015)
Answer:

Question 38.
If y = e ^{m sin -1 x} , then show that
(1 – x ² )\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) – m ² y = 0. (All India 2015).
Answer:
Given y = e ^{m sin -1 x}
On differentiating both sides w.r.t x, we get,

Question 39.
If f(x) = \(\sqrt{x^{2}+1}\); g(x) = \(\frac{x+1}{x^{2}+1}\) and h(x) = 2x – 3 then find f’[h’{g’(x)}]. (All India 2015).
Answer:

Question 40.
If y = \(\left(x+\sqrt{1+x^{2}}\right)^{n}\), then show that (1 + x ² )\(\frac{d^{2} y}{d x^{2}}\) + x\(\frac{d y}{d x}\) = n ² y. (Foregin 2015).
Answer:

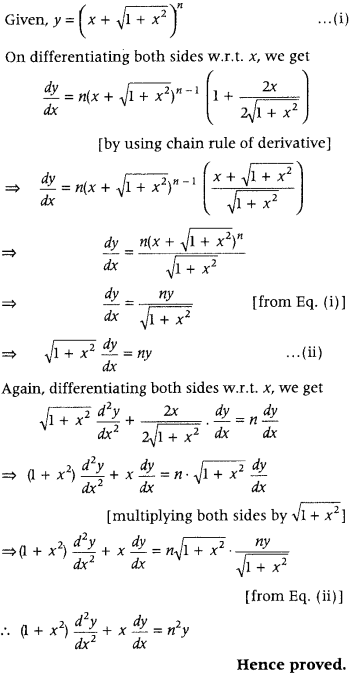
Question 41.
Find whether the following function is differentiable at x = 1 and x = 2 or not. (Foreign 2015).

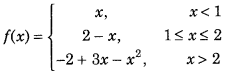
Answer:

∵ LHD = RHD
So, f(x) is differentiable at x = 2
Hence, f(x) is not differentiable at x = 1, but it differentiable at x = 2

Question 42.
For what value of λ, the function defined by

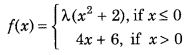
is continuous at x = 0? Hence, check the differentiability of f(x) at x = 0. (All India 2015C)
Answer:

Question 43.
If y = (sin x) ^x + sin ^-1 √x,then find \(\mathrm{d} \frac{d y}{d x}\). (Delhi 2015C, 2013C)
Answer:
Given, y = (sin x) ^x + sin ^-1 √x …… (i)
Let u = (sin x) ^x ……. (ii)
Then, Eq. (i) becomes, y = u + sin ^-1 √x ….. (iii)
On taking log both sides of Eq. (ii), we get
log u = x log sin x
On differentiating both sides w.r.t. x, we get

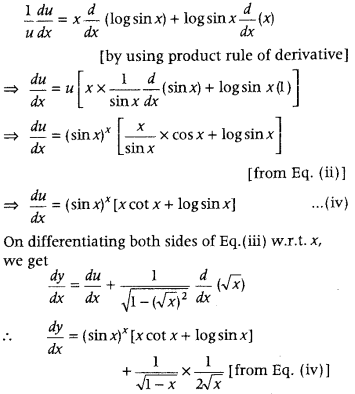
Question 44.
If y = \(\frac{x \cos ^{-1} x}{\sqrt{1-x^{2}}}\) – l0g\(\sqrt{1-x^{2}}\), then prove that \(\frac{d y}{d x}=\frac{\cos ^{-1} x}{\left(1-x^{2}\right)^{3 / 2}}\) (Delhi 2015C)
Answer:

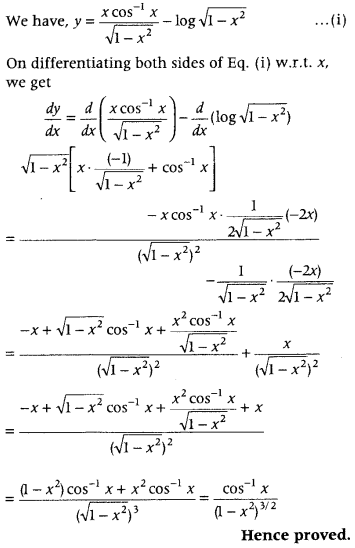
Question 45.
Write the derivative of sin x with respect to cos x. (Delhi 2014C)
Answer:
Let u = sin x
On differentiating both sides w.r.t. X, we get
\(\frac{d u}{d x}\) = cos x ……. (i)
Also, let v = cos x
On differentiating both sides w.r.t. x, we get
\(\frac{d v}{d x}\) = – sin x ……… (ii)
Now, \(\frac{d u}{d v}=\frac{d u}{d x} \times \frac{d x}{d v}=-\frac{\cos x}{\sin x}\) [from Eqs. (i) and (ii)]
∴ \(\frac{d u}{d v}\) = – cot x

Question 46.
If y = sin ^-1 {x,\(\sqrt{1-x}\) – \(\sqrt{1-x^{2}}\)} and 0 < x < 1, then find \(\frac{d y}{d x}\). (All India 2014C; Delhi 2010)
Answer:
First, convert the given expression in sin ^-1 [x \(\sqrt{1-y^{2}}\) – y\(\sqrt{1-x^{2}}\)] form and then put x = sin Φ and y = sin Φ. Now, simplify the resulting expression and differentiate it.

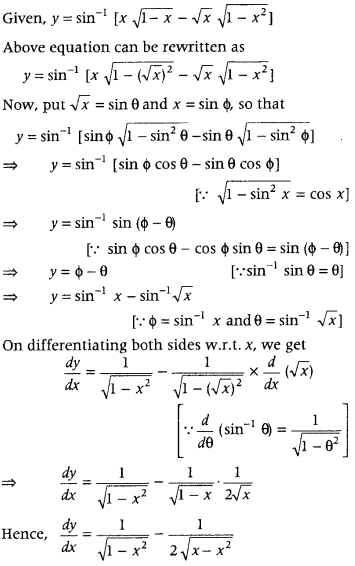
Question 47.
If e ^x + e ^y = e ^{x + y} , prove that \(\frac{d y}{d x}\) + e ^{y – x} = 0. (Foreign 2014)
Answer:
Given, e ^x + e ^y = e ^{x + y} ………… (i)
On dividing Eq.(i) by e ^{x + y} , we get
e ^-y + e ^-x = 1 ………. (ii)
On differentiating both sides of Eq. (ii) w.r.t. x,
We get

Question 48.
Find the value of \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{4}\), if
x = ae ^θ (sin θ – cos θ) and
y = ae ^θ (sin θ + cos θ). (All IndIa 2014)
Answer:

Question 49.
If x = α(cos t + log tan\(\frac{t}{2}\)) y = a sin t, then evaluate \(\frac{d^{2} y}{d x^{2}}\) at t = \(\frac{\pi}{3}\). (Delhi 2014C)
Answer:
\(\frac{8 \sqrt{3}}{a}\)

Question 50.
If x ^m y ^m = (x + y) ^{m + n} , prove that \(\frac{d y}{d x}=\frac{y}{x}\). (Foreign 2014)
Answer:
First, take log on both sides. Further, differentiate it to prove the required result.
Given x ^m y ⁿ = (x + y) ^{m + n}
On taking log both sides, we get
log (x ^m y ^m ) = log(x + y) ^{m + n}
⇒ log(x ^m ) + log(y ⁿ ) = (m + n) log(x + y)
⇒ m log x + n log y = (m + n) log (x + y)
On differentiating both sides W:r.t. x, we get

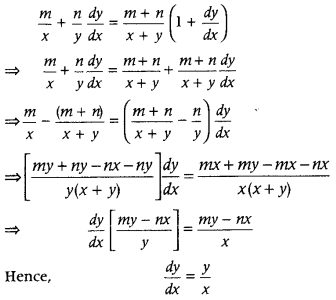
Question 51.
Differentiate tan ^-1 \(\left(\frac{\sqrt{1-x^{2}}}{x}\right)\) w.r.t. cos ^-1 (2x\(\sqrt{1-x^{2}}\)), when x ≠ 0. (Delhi 2014)
Answer:

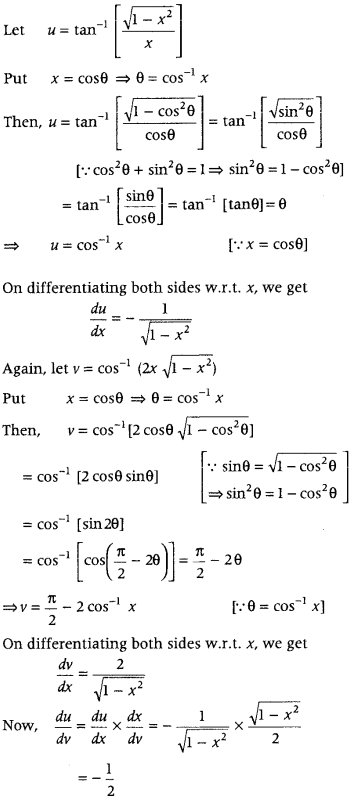
Question 52.
Differentiate tan ^-1 \(\left(\frac{x}{\sqrt{1-x^{2}}}\right)\) w.r.t. sin ^-1 (2x \(\sqrt{1-x^{2}}\)). (Delhi 2014)
Answer:

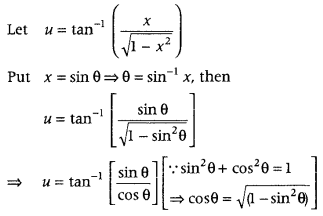
Question 53.
If y = Pe ^ax + Qe ^bx , then show that \(\) – (a + b) \(\) + aby = 0. (All India 2014)
Answer:

Question 54.
If x = cos t(3 – 2 cos ² t)and y = sin t (3 – 2 sin ² t), then find the value of \(\frac{d y}{d x}\) at t = \(\frac{\pi}{4}\). (All India 2014)
Answer:
Given, x = cos t(3 – 2 cos ² t)
⇒ x = 3 cos t – 2 cos ³ t
On differentiating both sides w.r.t. t, we get
\(\frac{d x}{d t}\) = 3(- sin t) – 2(3) cos ² t (- sin t)
⇒ \(\frac{d x}{d t}\) =- 3 sin t + 6 cos t sin t ….. (i)
Also, y = sin t (3 – 2sin ² t)
⇒ y = 3 sin t – 2 sin ³ t
On differentiating both sides w.r.t. t, we get
\(\frac{d y}{d t}\) = 3 cos t – 2 × 3 × sin ² t cos t

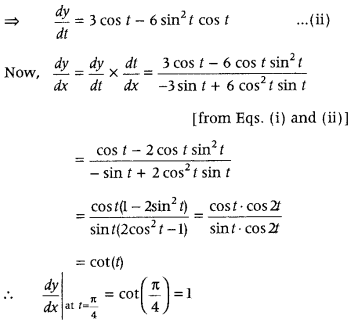
Question 55.
If (x – y) \(e^{\frac{x}{x-y}}\) = a, prove that y \(\frac{d y}{d x}\) + x = 2y. (Delhi 2014C)
Answer:

Question 56.
If x = a(cos t + t sin t)and y = a (sin t – t cos t), then find the value of \(\frac{d^{2} y}{d x^{2}}\) at t = \(\frac{\pi}{4}\). (Delhi 2014C)
Answer:
\(\frac{8 \sqrt{2}}{a \pi}\)

Question 57.
If y = tan ^-1 \(\left(\frac{a}{x}\right)\) + log \(\sqrt{\frac{x-a}{x+a}}\), prove that \(\frac{d y}{d x}=\frac{2 a^{3}}{x^{4}-a^{4}}\) (All India 2014C)
Answer:

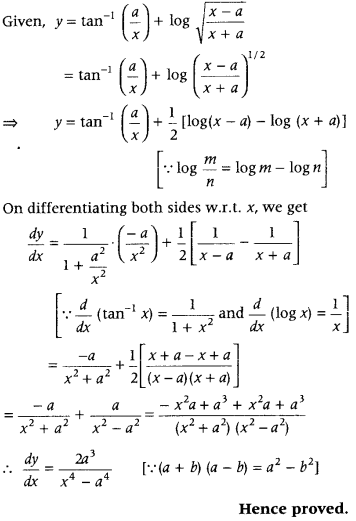
Question 58.
If (tan ^-1 x) ^y + y ^{cot x} = 1, then find dy/dx. (All India 2014C)
Answer:
Let u = (tan ^-1 x) ^y and v = y ^{cot x}
Then, given equation becomes u + y = 1
On differentiating both sides w.r.t. x, we get
\(\frac{d u}{d x}+\frac{d v}{d x}\) = 0 ……. (i)
Now, u = (tan ^-1 x)
On taking log both sides, we get
log u = y 1og(tan ^-1 x)
On differentiating both sides w.r.t. x, we get

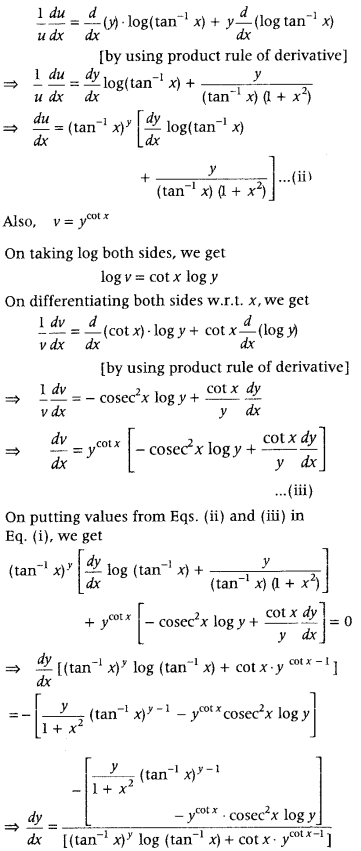
Question 59.
If x = 2 cos θ – cos 2θ and y = 2 sin θ – sin 2θ, then prove that \(\frac{d y}{d x}\) = tan \(\left(\frac{3 \theta}{2}\right)\). (Delhi 2013C)
Answer:
Given x = 2 cos θ – cos 2θ
and y = 2 sin θ – sin 2θ
On differentiating both sides w.r.t θ, we get

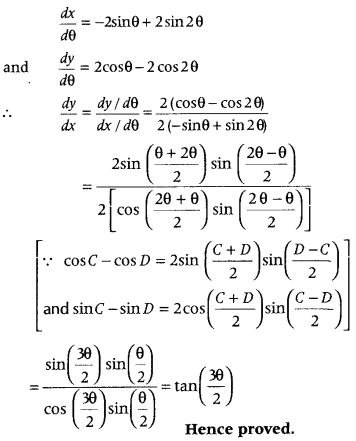
Question 60.
If y = x log \(\left(\frac{x}{a+b x}\right)\), then prove that x ³ \(\frac{d^{2} y}{d x^{2}}\) = \(\left(x \frac{d y}{d x}-y\right)^{2}\). (Delhi 2013C)
Answer:

Question 61.
If x = cos θ and y = sin ³ θ, then prove that \(y \frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{2}\) = 3 sin ² θ(5 cos ² θ – 1). (All India 2013C)
Answer:
Given x = cos θ ……. (i)
and y = sin ³ θ ……. (ii)
On differentiating both sides of Eqs. (i) and (ii) w.r.t θ, we get

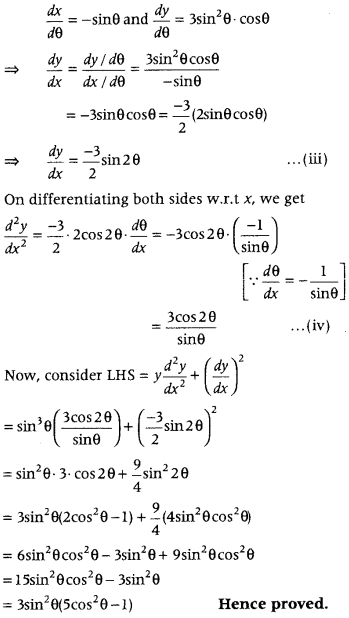
Question 62.
Differentiate the following function with respect to x.
(log x) ^x + x ^{log x} (Delhi 2013)
Answer:
Let y = (log x) ^x + x ^{log x}
Also, let u = (log x) ^x and v = x ^{log x} , then y = u + v
⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) …… (i)
Now, consider u = (log x) ^x
On taking log both sides, we get
log u = log (log x) ^x = x log(log x)
On differentiating both sides w.r.t. x, we get

Question 63.
If y = log[x + \(\sqrt{x^{2}+a^{2}}\)], then show that (x ² + a ² )\(\frac{d^{2} y}{d x^{2}}\) + x\(\frac{d y}{d x}\) = 0 (Delhi 2013)
Answer:

Question 64.
Show that the function f(x) = |x – 3|, x ∈ R, is continuous but not differentiable at x = 3. (Delhi 2013)
Answer:

Question 65.
If x = a sin t and y = a[cos t + log tan (t/2)], then find \(\frac{d^{2} y}{d x^{2}}\) (Delhi 2013)
Answer:
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{-{cosec}^{2} t}{a \cos t}\)

Question 66.
Differentiate the following with respect to x.
sin ^-1 \(\left[\frac{2^{x+1} \cdot 3^{x}}{1+(36)^{x}}\right]\) (All India 2013)
Answer:
First, put 6 ^x equal to tan θ. so that it becomes some standard trigonometric function. Then, simplify the expression and then differentiate by using chain rule.

Question 67.
If x = a cos ³ θ and y = a sin ³ θ, then find the value of \(\frac{d^{2} y}{d x^{2}}\) at θ = \(\frac{\pi}{6}\). (All lndia 2013)
Answer:

Question 68.
If x sin(a + y) + sin a cos(a + y) = 0, then prove that = \(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\). (All IndIa 2013)
Answer:

Question 69.
If x ^y = e ^{x – y} , then prove that \(\frac{d y}{d x}=\frac{\log x}{(1+\log x)^{2}}\) (All India 2013, Delhi 2010)
Or
If x ^y = e ^{x – y} , then prove that (All India 2011)
\(\frac{d y}{d x}=\frac{\log x}{\{\log (x e)\}^{2}}\)
Answer:
First, take log on both sides and convert it into y = f(x) form. Then, differentiate both sides to get required result.
Given, x ^y = e ^{x – y}
On taking log both sides, we get
y log _e x = (x – y)log _e e
⇒ y log _e x = x – y [∵ log _e e = 1]
⇒ y(1 + log x) = x
⇒ y = \(\frac{x}{1+\log x}\)
On differentiating both sides w.r.t x, we get

Question 70.
If y ^x = e ^{x – y} , then prove that
\(\frac{d y}{d x}=\frac{(1+\log y)^{2}}{\log y}\) (All India 2013)
Answer:
First, take log on both sides and convert it into y = f(x) form. Then, differentiate both sides to get required result.
Given, x ^y = e ^{x – y}
On taking log both sides, we get
y log _e x = (x – y)log _e e
⇒ y log _e x = x – y [∵ log _e e = 1]
⇒ y(1 + log x) = x
⇒ y = \(\frac{x}{1+\log x}\)
On differentiating both sides w.r.t x, we get

Question 71.
If sin y = x sin(a + y), then prove that
\(\frac{d y}{d x}=\frac{\sin ^{2}(a+y)}{\sin a}\) (Delhi 2012)
Answer:

Question 72.
If y = sin ^-1 x, show that
(1 – x ² )\(\frac{d^{2} y}{d x^{2}}\) – x\(\frac{d y}{d x}\) = 0.
Answer:
Given y = (sin ^-1 x) ²
Differentiating on w.r.t x, we get

Question 73.
If x = \(\sqrt{a^{\sin ^{-1} t}}\) and y = \(\sqrt{a^{\cos ^{-1} t}}\) then show that \(\frac{d y}{d x}=\frac{-y}{x}\). (All India 2012)
Answer:

Question 74.
Differentiate tan ^-1 \(\left[\frac{\sqrt{1+x^{2}}-1}{x}\right]\) w.r.t. x. (All India 2012)
Answer:
\(\frac{l}{2\left(1+x^{2}\right)}\)

Question 75.
If y = (tan ^-1 x) ² , then show that (x ² + 1) ² \(\frac{d^{2} y}{d x^{2}}\) + 2x(x ² + 1)\(\frac{d y}{d x}\) = 2 (Delhi 2012)
Answer:

Question 76.
If y = x ^{sin x – cos x} + \(\), then find \(\). (Delhi 2012C)
Answer:

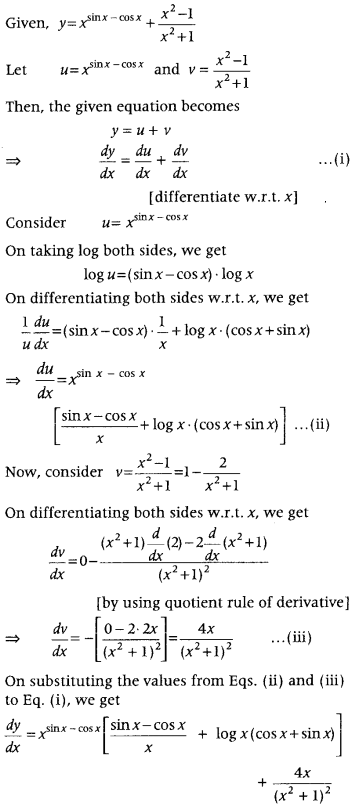
Question 77.
If x = a(cos t + t sin t) and y = a(sin t – t cos t), then find \(\frac{d^{2} x}{d t^{2}}, \frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\). (All India 2012)
Answer:
Given x = a(cos t + t sin t)
On differentiating both sides w.r.t t, we get

Question 78.
If x = a(cos t + log tan \(\frac{t}{2}\)) and y = a sin t, find \(\frac{d^{2} y}{d t^{2}}\) and \(\frac{d^{2} y}{d x^{2}}\). (All India 2012)
Answer:
\(\frac{d^{2} y}{d x^{2}}\) = \(\frac{\sin t \sec ^{4} t}{a}\)
Also, \(\frac{d^{2} y}{d t^{2}}\) = \(\frac{d}{d t}\left(\frac{d y}{d t}\right)\) = \(\frac{d}{d t}\)(a cos t) = – a sin t

Question 79.
Find \(\frac{d y}{d x}\), when y = x ^{cot x} + \(\frac{2 x^{2}-3}{x^{2}+x+2}\) (All IndIa 2012C)
Answer:

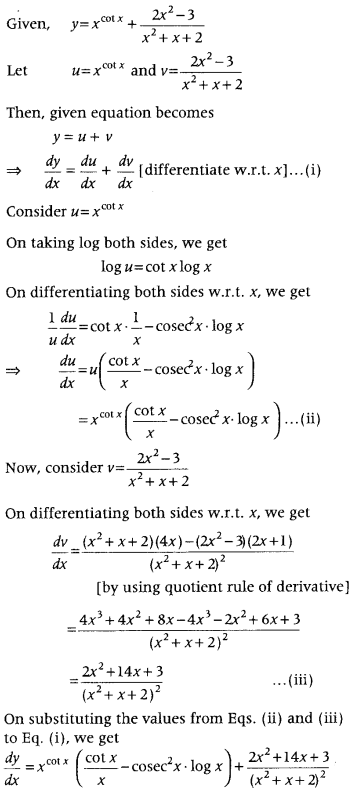
Question 80.
If x = tan\(\left(\frac{1}{a} \log y\right)\), then show that (1 + x ² )\(\frac{d^{2} y}{d x^{2}}\) + (2x – a)\(\frac{d y}{d x}\) = 0 (All India 2011)
Answer:

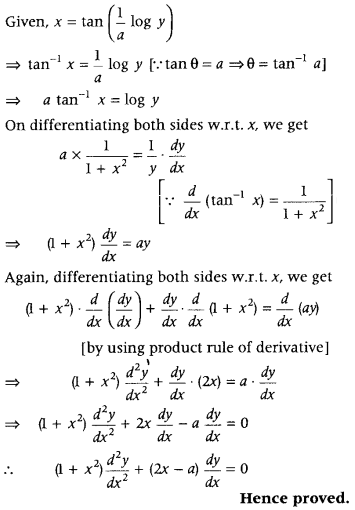
Question 81.
Differentiate x ^{x cos x} + \(\frac{x^{2}+1}{x^{2}-1}\) w.r.t x. (Delhi 2011)
Answer:
x ^{x cos x} [cos x – x log x sin x + log x cos x + \(\frac{4 x}{\left(x^{2}-1\right)^{2}}\)

Question 82.
If x = a (θ – sin θ), y = a (1 + cos θ), then find \(\frac{d^{2} y}{d x^{2}}\). (Delhi 2011)
Answer:

Question 83.
Prove that
\(\frac{d}{d x}\left[\frac{x}{2} \sqrt{a^{2}-x^{2}}+\frac{a^{2}}{2} \sin ^{-1}\left(\frac{x}{a}\right)\right]\) = \(\sqrt{a^{2}-x^{2}}\) (Foregin 2011)
Answer:

Question 84.
If y = log[x + \(\sqrt{x^{2}+1}\)], then prove that (x + 1)\(\frac{d^{2} y}{d x^{2}}\) + x\(\frac{d y}{d x}\) = 0. (Foreign 2011)
Answer:

Question 85.
If log(\(\sqrt{1+x^{2}}\) – x) = y\(\sqrt{1+x^{2}}\), then show that (1 + x ² )\(\frac{d y}{d x}\) + xy + 1 = 0. (All India 2011C)
Answer:

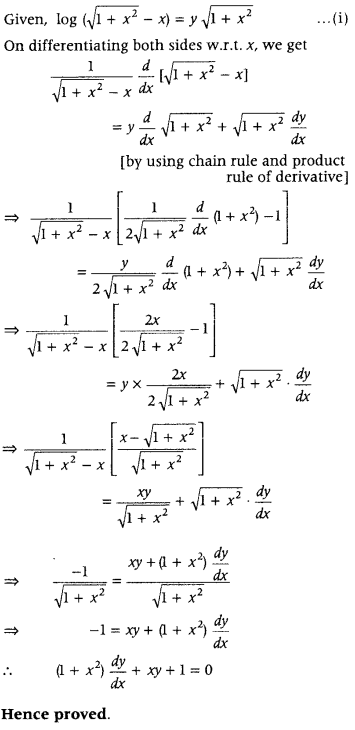
Question 86.
If x = a(θ + sin θ) and y = a(1 – cos θ),then find \(\) (All India 2011C)
Answer:
\(\frac{1}{4 a} \sec ^{4} \frac{\theta}{2}\)

Question 87.
If y = a sin x + b cos x, then prove that y ² + \(\left(\frac{d y}{d x}\right)^{2}\) = a ² + b ² . (All India 2011C)
Answer:
First, we differentiate the given expression with respect to x and get first derivative of y. Then, put the value of y and first derivative of y in LHS of given expression and then solve it to get the required RHS.
To prove y ² + \(\left(\frac{d y}{d x}\right)^{2}\) = a ² + b ²
Given, y = a sin x + b cos x ….. (ii)
On differentiating both sides of Eq. (ii) w.r.t. x,
we get
\(\frac{d y}{d x}\) = a cos x – b sin x
Now, Let us take LHS of Eq. (i).
Here, LHS = y ² + \(\left(\frac{d y}{d x}\right)^{2}\)
On putting the value of y and dy/dx , we get
LHS = (a sin x + b cos x) ² + (a cos x – b sin x) ²
= a ² sin ² x + b ² cos ² x + 2ab sin x cos x + a ² cos ² x + b ² sin ² x – 2ab sin x cos x
= a ² sin ² x + b ² cos ² x + a ² cos ² x + b ² sin ² x
= a ² (sin ² x + cos ² x) + b ² (sin ² x + cos ² x)
= a ² + b ² [∵ sin ² x + cos ² x = 1]
= RHS
Hence proved.

Question 88.
If x = a(cos θ + θ sin θ) and y = a(sin θ – θ cos θ), then find \(\frac{d^{2} y}{d x^{2}}\) (All India 2011C)
Answer:
\(\frac{\sec ^{3} \theta}{a \theta}\)

Question 89.
If x = a(θ – sin θ) and y = a(1 + cos θ), then find \(\frac{d y}{d x}\) at θ = \(\frac{\pi}{3}\). (Delhi 2011C)
Answer:
Given x = a(θ – sin θ)
and y = a(1 + cos θ)
On differentiating both sides w.r.t. θ, we get

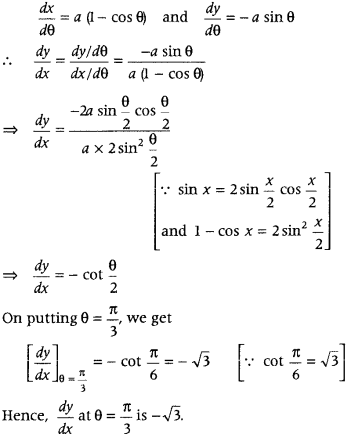
Question 90.
If y (sin x – cos x) ^{(sin x – cos x)} , \(\frac{\pi}{4}\) < x < \(\frac{3 \pi}{4}\), then find \(\frac{d y}{d x}\). (All India 2010C)
Answer:
First, take log on both sides and then differentiate to get the required value of \(\frac{d y}{d x}\).

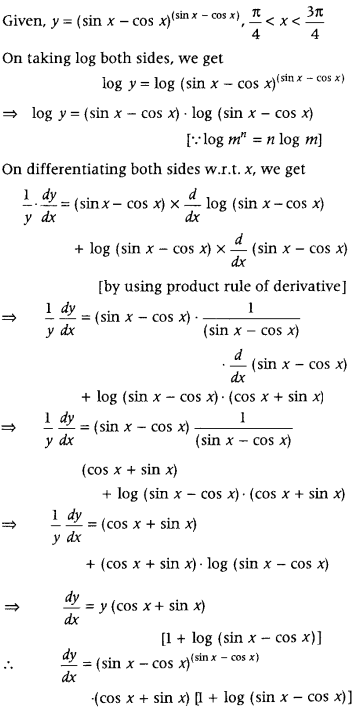
Question 91.
If y = cos ^-1 \(\left[\frac{2 x-3 \sqrt{1-x^{2}}}{\sqrt{13}}\right]\), then find \(\frac{d y}{d x}\). (All India 2010C)
Answer:
In the given expression, put x = sin θ and simplify the resulting expression, then differentiate it.

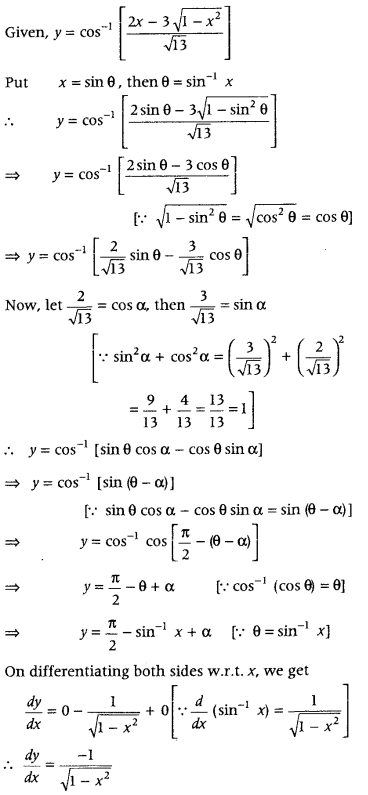
Question 92.
If y = (cot ^-1 x) ² , then show that
(x ² + 1) ² \(\frac{d^{2} y}{d x^{2}}\) + 2x(x ² + 1)\(\frac{d y}{d x}\) = 2. (Delhi 2010C)
Answer:

Question 93.
If y = cosec ^-1 x, x > 1, then show that x(x ² – 1)\(\frac{d^{2} y}{d x^{2}}\) + (2x ² – 1)\(\frac{d y}{d x}\) = 0 (All India 2010)
Answer:
Given y = cosec ^-1 x
On differentiating both sides w.r.t. x, we get

Question 94.
If y = cos ^-1 \(\left(\frac{3 x+4 \sqrt{1-x^{2}}}{5}\right)\), then find \(\frac{d y}{d x}\). (All India 2010)
Answer:
\(\frac{1}{\sqrt{1-x^{2}}}\)

Question 95.
Show that the function defined as follows, is continuous at x = 1, x = 2 but not differentiable at x = 2. (Delhi 2010)

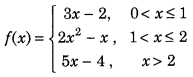
Answer:

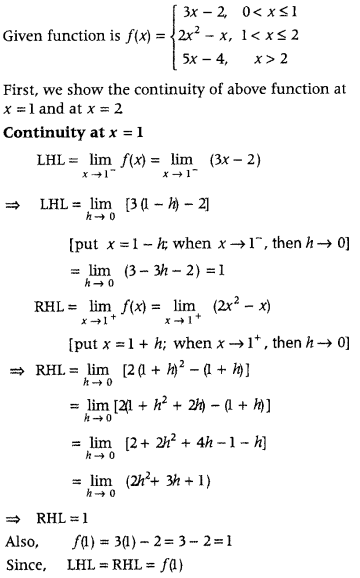
Continuity at x = 2:

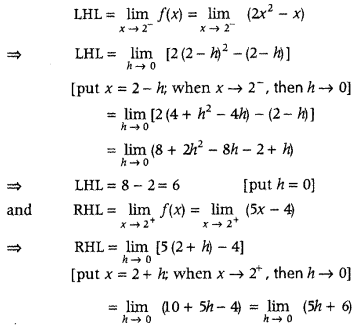
⇒ RHL = 6
Also, f(2) = 2(2) ² – 2 = 8 – 2 = 6
Since, LHL = RHL = f(2)
∴ f(x) is continuous at x = 2
Hence, f(x) is continuous at all indicated points.
Now, let us verify differentiability of the given function at x = 2

Differentiability at x = 2:

Since, LHD ≠ RHD
So, f(x) is not differentiable at x = 2
Hence. f(x) is continuous at x = 1 and x = 2 but not differentiable at x = 2
Hence Proved.

Question 96.
If y = e ^{a cos -1 x} , – 1 ≤ x ≤ 1, then show that
(1 – x ² )\(\frac{d^{2} y}{d x^{2}}\) – x \(\frac{d y}{d x}\) – a ² y = 0. (All IndIa 2010)
Answer:
Given y = e ^{m sin -1} x
On differentiating both sides w.r.t x, we get,

Question 97.
Find \(\frac{d y}{d x}\), if y = (cos x) ^x + (sin x) ^1/x . (Delhi 2010)
Answer:
Given, y = (cos x) ^x + (sin x) ^1/x
Let u = (cos x) ^x and v = (sin x) ^1/x
Then, given equation becomes
y = u + v
on differentiating both sides w.r.t x, we get
⇒ \(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\)
Consider, u = (cos x) ^x
On taking log both sides, we get
log u = log (cos x) ^x
⇒ log u = x log (cos X)
[∵ log m ⁿ = n log m]
On differentiating both sides w.r.t. x, we get

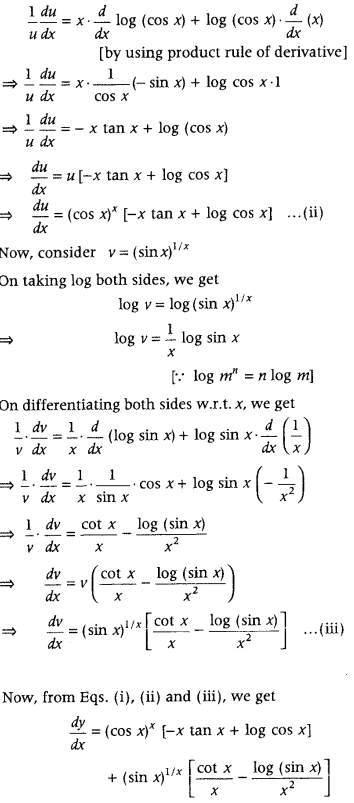
Question 98.
If y = e ^x sin x, then prove that
\(\frac{d^{2} y}{d x^{2}}\) – 2\(\frac{d y}{d x}\) + 2y = 0. (All India 2010C)
Answer:
First, find \(\frac{d y}{d x}\) and \(\frac{d^{2} y}{d x^{2}}\) and then put their values along with value of y in LHS of proven expression.

Question 99.
If y = (x) ^x + (sin x) ^x , then find \(\frac{d y}{d x}\) (All India 2010C).
Answer:
Given, y = (x) ^x + (sin x) ^x
Let u = (x) ^x
and v = (sin x) ^x
Then, given equation becomes, y = u + v
On differentiating both sides w.r.t. x, we get
\(\frac{d y}{d x}=\frac{d u}{d x}+\frac{d v}{d x}\) …….. (i)
Consider, u = x ^x
On taking log both sides, we get
log u = log x ^x
⇒ log u = x log x [∵ log m ⁿ = n log m]