Determinants Class 12 Maths Important Questions Chapter 4

Get access to Class 12 Maths Important Questions Chapter 4 Determinants, Determinants Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.

Determinants Class 12 Important Questions with Solutions Previous Year Questions

Expansion of Determinant

Question 1.
Find |AB|, if A = \(\left[\begin{array}{rr}
0 & -1 \\
0 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{ll}
3 & 5 \\
0 & 0
\end{array}\right]\). (All India 2019)
Answer:

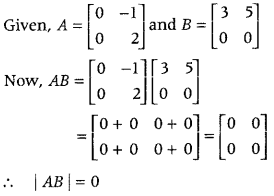
Question 2.
Find the maximum value of (Delhi 2016)
\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
1 & 1+\sin \theta & 1 \\
1 & 1 & 1+\cos \theta
\end{array}\right|\)
Answer:

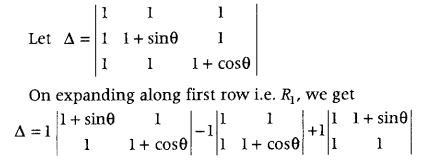
= [(1 + sinθ)(1 + cosθ) – 1] – [1 + cosθ – 1] + [1 – 1 – sinθ]
= 1 + cosθ + sinθ + sinθcosθ – 1 – cosθ – sinθ
= sinθcosθ
= |\(\frac{1}{2}\)|(2sinθcosθ) = \(\frac{1}{2}\)sin2θ
We know that, maximum value of sin 2θ is 1.
∴ Δ _max = \(\frac{1}{2}\) × 1 = \(\frac{1}{2}\)

Question 3.
If \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\) = 8, write the value of x. (Foreign 2016)
Answer:
We have, \(\left|\begin{array}{ccc}
x & \sin \theta & \cos \theta \\
-\sin \theta & -x & 1 \\
\cos \theta & 1 & x
\end{array}\right|\) = 8

On expanding along R ₁ , we get
x (- x ² -1) – sinθ(- x sinθ – cosθ) + cosθ(- sinθ + x cosθ) = 8
⇒ – x ³ – x + x sin ² θ + sinθcosθ – sinθcosθ + x cos2θ = 8
⇒ – x ³ – x + x (sin ² θ + cos ² θ) = 8
⇒ -x ³ – x + x = 8 [∵ sin ² θ + cos ² θ = 1]
⇒ – x ³ = 8 ⇒ x ³ + 8 = 0 ⇒ x ³ + 2 ³ = 0
⇒ (x + 2)(x ² + 4 – 2x) = 0
⇒ x = -2 [∵ x ² – 2x + 4 = 0, gives imaginary values]

Question 4.
If A = \(\left[\begin{array}{ccc}
5 & 6 & -3 \\
-4 & 3 & 2 \\
-4 & -7 & 3
\end{array}\right]\), then write the cofactor of the element a ₂₁ of its 2nd row. (Foreign 2015)
Answer:
Given, A = \(\left[\begin{array}{ccc}
5 & 6 & -3 \\
-4 & 3 & 2 \\
-4 & -7 & 3
\end{array}\right]\)

Now, Cofactors of a ₂₁ = (-1)\(\left|\begin{array}{cc}
6 & -3 \\
-7 & 3
\end{array}\right|\)
= -(18 – 21) = 3

Question 5.
If A = \(\left[\begin{array}{cc}
1 & 2 \\
3 & -1
\end{array}\right]\) and B = \(\left[\begin{array}{cc}
1 & 3 \\
-1 & 1
\end{array}\right]\), write the value of |AB|. (Delhi 2015C)
Answer:
Clearly, |A| = \(\left|\begin{array}{cc}
1 & 2 \\
3 & -1
\end{array}\right|\) = -1 – 6 = – 7
and |B| = \(\left|\begin{array}{cc}
1 & 3 \\
-1 & 1
\end{array}\right|\) = 1 + 3 = 4
∴ |AB| = |A|.|B| = (-7)(4) = -28

Question 6.
In the interval it π/2 < x < π, find the value of x for which the matrix \(\left[\begin{array}{cc}
2 \sin x & 3 \\
1 & 2 \sin x
\end{array}\right]\) is singular. (All India 2015C)
Answer:

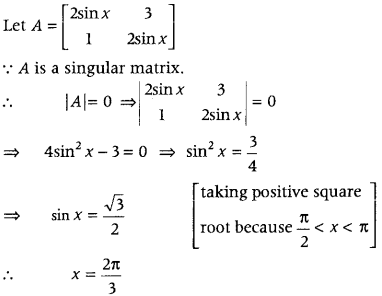
Question 7.
If \(\left|\begin{array}{rr}
2 x & 5 \\
8 & x
\end{array}\right|=\left|\begin{array}{rr}
6 & -2 \\
7 & 3
\end{array}\right|\), then write the value of x. (Delhi 2014)
Answer:
First, expand both determinants, which gives ” equation in x and then solve that equation to find the value of x.
Given, \(\left|\begin{array}{rr}
2 x & 5 \\
8 & x
\end{array}\right|=\left|\begin{array}{rr}
6 & -2 \\
7 & 3
\end{array}\right|\)
⇒ 2x ² – 40 = 18 -(-14)
⇒ 2x ² – 40 = 32
⇒ 2x ² = 72
⇒ x ² = 36
∴ x = ± 6

Question 8.
If = \(\left|\begin{array}{cc}
3 x & 7 \\
-2 & 4
\end{array}\right|=\left|\begin{array}{cc}
8 & 7 \\
6 & 4
\end{array}\right|\), then find the value of x. (All India 2014)
Answer:
Given, \(\left|\begin{array}{cc}
3 x & 7 \\
-2 & 4
\end{array}\right|=\left|\begin{array}{cc}
8 & 7 \\
6 & 4
\end{array}\right|\)
x = -2

Question 9.
Write the value of the determinant (Delhi 2014C)
\(\left|\begin{array}{cc}
p & p+1 \\
p-1 & p
\end{array}\right|\)
Answer:
Let Δ = \(\left|\begin{array}{cc}
p & p+1 \\
p-1 & p
\end{array}\right|\)

On expanding, we get
Δ = p ² – (p – 1)(p + 1)
⇒ Δ = p ² – (p ² – 1 ² ) [∵ a ² – b ² =(a + b) (a – b)]
⇒ Δ = p ² – p ² + 1
∴ Δ = 1

Question 10.
If \(\left|\begin{array}{cc}
2 x & x+3 \\
2(x+1) & x+1
\end{array}\right|=\left|\begin{array}{ll}
1 & 5 \\
3 & 3
\end{array}\right|\), then find the value of x. (Delhi 2013C)
Answer:
Expand both determinants which gives equation in x and then solve that equation to find the value of x.
Given, \(\left|\begin{array}{cc}
2 x & x+3 \\
2(x+1) & x+1
\end{array}\right|=\left|\begin{array}{ll}
1 & 5 \\
3 & 3
\end{array}\right|\)
⇒ 2x (x +1) – (x + 3) (2x + 2) = 3 – 15
⇒ 2x ² + 2x – (2x ² + 8x + 6) = -12
⇒ – 6x – 6 =-12 ⇒ 6x = 6
∴ x = 1

Question 11.
If \(\left|\begin{array}{ll}
x+1 & x-1 \\
x-3 & x+2
\end{array}\right|=\left|\begin{array}{cc}
4 & -1 \\
1 & 3
\end{array}\right|\), then write the value of x. (Delhi 2013)
Answer:
Given, \(\left|\begin{array}{ll}
x+1 & x-1 \\
x-3 & x+2
\end{array}\right|=\left|\begin{array}{cc}
4 & -1 \\
1 & 3
\end{array}\right|\)
∴ x = 2

Question 12.
If A _ij is the cofactor of the element a of the determinant \(\left|\begin{array}{ccc}
2 & -3 & 5 \\
6 & 0 & 4 \\
1 & 5 & -7
\end{array}\right|\), then write the value of a ₃₂ . A ₃₂ . (All India 2013)
Answer:
Let Δ = \(\left|\begin{array}{ccc}
2 & -3 & 5 \\
6 & 0 & 4 \\
1 & 5 & -7
\end{array}\right|\)
Here, a ₃₂ = 5
Given, A _ij is the cofactor of the element a _ij of A.
∴ A ₃₂ = (-1) ³⁺² \(\left|\begin{array}{ll}
2 & 5 \\
6 & 4
\end{array}\right|\) = -1(8 – 30) = 32
⇒ a ₃₂ . A ₃₂ = 5 × 32 = 110

Question 13.
If Δ = \(\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\), write the cofactor of a ₂₃ . (Delhi 2012)
Answer:
Cofactor of element a ₃₂
= (-1) ³⁺² \(\left|\begin{array}{ll}
5 & 8 \\
2 & 1
\end{array}\right|\) = (-1)(5 – 16) = 11

Question 14.
If Δ = \(\left|\begin{array}{lll}
1 & 2 & 3 \\
2 & 0 & 1 \\
5 & 3 & 8
\end{array}\right|\), write the minor of element a ₂₂ . (Delhi 2012)
Answer:
Minor of elements a ₂₂ = \(\left|\begin{array}{ll}
1 & 3 \\
5 & 8
\end{array}\right|\) = 8 – 15 = -7

Question 15.
If Δ = \(=\left|\begin{array}{lll}
5 & 3 & 8 \\
2 & 0 & 1 \\
1 & 2 & 3
\end{array}\right|\), then write the minor of the element a ₂₃ . (Delhi 2012)
Answer:
Minor of the elements a ₂₃ = \(\left|\begin{array}{ll}
5 & 3 \\
1 & 2
\end{array}\right|\) = 10 – 3 = 7

Question 16.
For what value of x, A = \(\left[\begin{array}{cc}
2(x+1) & 2 x \\
x & x-2
\end{array}\right]\) is a singular matrix? (All India 2011C)
Answer:
For a singular matrix, |A| = 0. Use this relation and solve it.
We know that, a matrix A is said to be singular, if |A| = 0
∴ \(\left[\begin{array}{cc}
2(x+1) & 2 x \\
x & x-2
\end{array}\right]\) = 0
⇒ (2x + 2)(x – 2) – 2x ² = 0
⇒ 2x ² – 2x – 4 – 2x ² = 0
⇒ -2x = 4
∴ x = -2

Question 17.
For what value of x, the matrix \(\left[\begin{array}{cc}
2 x+4 & 4 \\
x+5 & 3
\end{array}\right]\) is a singular matrix? (All India 2011C)
Answer:
Let, A = \(\left[\begin{array}{cc}
2 x+4 & 4 \\
x+5 & 3
\end{array}\right]\)
If matrix A is singular, then
|A| = 0
⇒ \(\left|\begin{array}{cc}
2 x+4 & 4 \\
x+5 & 3
\end{array}\right|\) = 0
⇒ (2x + 4) × 3 – (x + 5) × 4 = 0
⇒ 6x + 12 – 4x – 20 = 0 ⇒ 2x = 8
∴ x = 4

Question 18.
For what value of x, the matrix \(\left[\begin{array}{cc}
2 x & 4 \\
x+2 & 3
\end{array}\right]\) is a singular matrix? (Delhi 2011C)
Answer:
Given, A = \(\left[\begin{array}{cc}
2 x & 4 \\
x+2 & 3
\end{array}\right]\)
∴ x = 4

Question 19.
For what value of x, matrix \(\left[\begin{array}{ll}
6-x & 4 \\
3-x & 1
\end{array}\right]\) is a singular matrix? (Delhi 2011C)
Answer:
Given A = \(\left[\begin{array}{ll}
6-x & 4 \\
3-x & 1
\end{array}\right]\)
∴ x = 2

Question 20.
For what value of x, the matrix \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\) is a singular? (Delhi 2011)
Answer:
Given A = \(\left[\begin{array}{cc}
5-x & x+1 \\
2 & 4
\end{array}\right]\)
∴ x = 3

Question 21.
Evaluate \(\left|\begin{array}{cc}
\cos 15^{\circ} & \sin 15^{\circ} \\
\sin 75^{\circ} & \cos 75^{\circ}
\end{array}\right|\). (All India 2011)
Answer:
Let Δ = \(\left|\begin{array}{cc}
\cos 15^{\circ} & \sin 15^{\circ} \\
\sin 75^{\circ} & \cos 75^{\circ}
\end{array}\right|\)

On expanding, we get
A = (cos 15° cos 75° – sin 15° sin 75°)
= cos (15° + 75°) [∵ cos x cos y – sin x sin y = cos (x + y)]
= cos 90° = 0 [∵ cos 90° = 0]

Question 22.
If \(\left|\begin{array}{ll}
x & x \\
1 & x
\end{array}\right|=\left|\begin{array}{ll}
3 & 4 \\
1 & 2
\end{array}\right|\), then write the positive value of x. (Foreign 2011; All India 2008C)
Answer:
Given, \(\left|\begin{array}{ll}
x & x \\
1 & x
\end{array}\right|=\left|\begin{array}{ll}
3 & 4 \\
1 & 2
\end{array}\right|\)
On expanding, we get
x ² – x = 6 – 4
⇒ x ² – x – 2 = 0
⇒ (x – 2)(x + 1) = 0
∴ x = 2 or -1
Hence, the positive value of x is 2.

Question 23.
What is the value of determinant \(\left|\begin{array}{lll}
0 & 2 & 0 \\
2 & 3 & 4 \\
4 & 5 & 6
\end{array}\right|\) ? (Delhi 2010)
Answer:
Determinant can be easily expand along that row or column which have maximum zeroes.
Let Δ = \(\left|\begin{array}{lll}
0 & 2 & 0 \\
2 & 3 & 4 \\
4 & 5 & 6
\end{array}\right|\)
Then, Δ = -1(12 – 16) [expanding along R ₁ ]
= -2(-4) = 8

Question 24.
Find the minor of the element of second row and third column (a ₂₃ ) in the following determinant \(\left|\begin{array}{ccc}
2 & -3 & 5 \\
6 & 0 & 4 \\
1 & 5 & -7
\end{array}\right|\). (Delhi 2010)
Answer:
Minor of elements a ₂₃ = 13

Question 25.
What positive value of x makes following pair of determinants equal? (All India 2010)
\(\left|\begin{array}{cc}
2 x & 3 \\
5 & x
\end{array}\right|,\left|\begin{array}{cc}
16 & 3 \\
5 & 2
\end{array}\right|\)
Answer:
Let \(\left|\begin{array}{cc}
2 x & 3 \\
5 & x
\end{array}\right|,\left|\begin{array}{cc}
16 & 3 \\
5 & 2
\end{array}\right|\)

On expanding, we get
2x ² – 15 = 32 – 15
⇒ 2x ² – 15 = 17
⇒ 2x ² = 32 ⇒ x ² = 16 ⇒ x = ± 4
Hence, for x = 4, given pair of determinants is equal.

Question 26.
If A = \(\left[\begin{array}{ll}
p & 2 \\
2 & p
\end{array}\right]\) and |A ³ | = 125 then find the value of p. (All India 2019)
Answer:
Given, A = \(\left[\begin{array}{ll}
p & 2 \\
2 & p
\end{array}\right]\)
∴ |A| = \(\left|\begin{array}{ll}
p & 2 \\
2 & p
\end{array}\right|\) = p ² – 4
and |A ³ | = 125 ⇒ |A| ³ = 125 [∵ |A| ³ = |A ³ |]
⇒ (p ² – 4) ³ = 125 ⇒ p ² – 4 = 5 ⇒ p ² = 9
⇒ p = ± 3

Properties of Determinants

Question 1.
If A is a square matrix satisfying A’A = I, write the value of |A|. (All India 2019)
Answer:
We have, A’A = I
⇒ |A’A| = |I| ⇒ |A’||A| = 1 [∵ | AB| = |A| |B|]
⇒ |A| ² = 1 [∵ |A’| = |A|]
⇒ |A| = ± 1

Question 2.
If A and B are square matrices of the same order 3, such that |A| = 2 and AB = 27. Write the value of |B|. (Delhi 2019)
Answer:
We know that,
(i) |kA| = k ⁿ |A|, if A is square matrix of nth order
(ii) |AB| = |A| × |B|
Here, we have AB = 21 and n – 3
∴ |AB| = |2I| = 2 ³ |I|= 8.1 = 8 [∵|I| = 1]
⇒ |4||B| = 8
⇒ 2.|B| = 8 ⇒ |B|=4

Question 3.
Write the value of Δ = \(\left|\begin{array}{ccc}
x+y & y+z & z+x \\
z & x & y \\
-3 & -3 & -3
\end{array}\right|\). (All India 2015)
Answer:

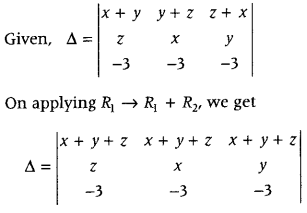
On taking (x + y + z) common from R ₁ and -3
Δ = (x + y + z)(-3)\(\left|\begin{array}{lll}
1 & 1 & 1 \\
z & x & y \\
1 & 1 & 1
\end{array}\right|\)
= (x + y + z)(-3) × 0 [∵ R ₁ and R ₃ are identical]
= 0

Question 4.
Write the value of \(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|\). (All India 2014C)
Answer:
Let Δ = \(\left|\begin{array}{lll}
2 & 7 & 65 \\
3 & 8 & 75 \\
5 & 9 & 86
\end{array}\right|\)
On applying C ₃ → C ₃ – 9C ₂ , we get
Δ = \(\left|\begin{array}{lll}
2 & 7 & 2 \\
3 & 8 & 3 \\
5 & 9 & 5
\end{array}\right|\)
= 0 [∵ C ₁ and C ₃ are identical]

Question 5.
Let A be a square matrix of order 3 × 3. Write the value of |2A|, where |A| = 4. (All India 2012)
Answer:
We know that, for a square matrix A of order n,
|kA| = k ⁿ – |A|
Here, |2A| = 2 ³ .|A| [∵ order of A is 3 × 3]
= 2 ³ × 4= 8 × 4 = 32 [put |A| = 4]

Question 6.
If the determinant of matrix A of order 3 × 3 is of value 4, then write the value of |3A|. (All India 2012C)
Answer:
We know that, for a square matrix A of order n,
|kA| = k ⁿ – |A|
Here, |3A| = 3 ³ .|A| [∵ order of A is 3 × 3]
= 108

Question 7.
Write the value of the determinant \(\left|\begin{array}{ccc}
102 & 18 & 36 \\
1 & 3 & 4 \\
17 & 3 & 6
\end{array}\right|\) (Foreign 2012)
Answer:

Question 8.
If A is a square matrix of order 3 and |3A| = k|A|, then write the value of k. (Delhi 2010)
Answer:
We know that, if A is a square matrix of order n. Then, |pA|= p ⁿ |A|
Here, the matrix A is of order 3 × 3.
∴ |3A| = (3) ³ |A| = 27|A|
On comparing with given equation, we get
k = 27

Question 9.
What is the value of \(\left|\begin{array}{lll}
4 & a & b+c \\
4 & b & c+a \\
4 & c & a+b
\end{array}\right|\)?
Answer:

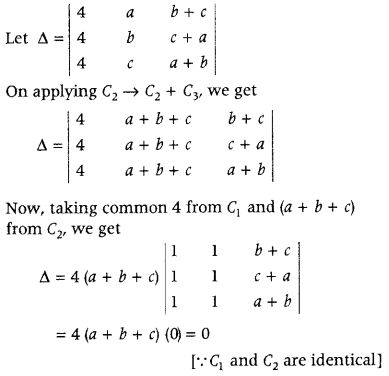
Question 10.
Using properties of determinants, show that (All India 2019)
\(\left|\begin{array}{ccc}
3 a & -a+b & -a+c \\
-b+a & 3 b & -b+c \\
-c+a & -c+b & 3 c
\end{array}\right|\) = 3(a + 6 + c) (ab + be + ca)
Answer:
Let the given determinant be A. Then,

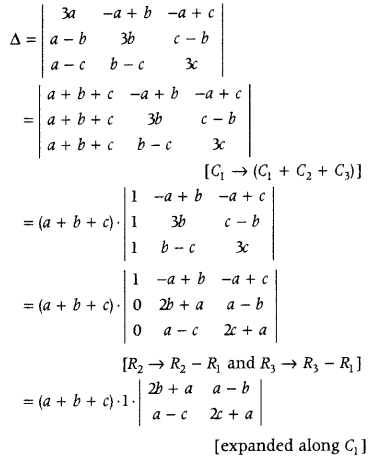
= (a + b + c) [(2b + a) (2c + a) – (a – c) (a – b)]
= (a + b + c) [(abc + 2ab + 2ac + a ² ) – (a ² – ab – ac + bc)]
= 3(a + b + c) (ab + bc + ca)
Hence, Δ = 3(a + b + c) (ab + bc + ca)

Question 11.
Using properties of determinants, prove the following (Delhi 2019)
\(\left|\begin{array}{ccc}
a+b+c & -c & -b \\
-c & a+b+c & -a \\
-b & -a & a+b+c
\end{array}\right|\) = 2(a + b) (b + c) (c + a)
Answer:

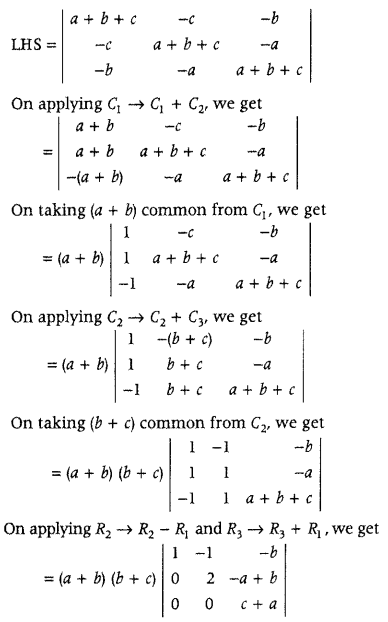
= (a + b) (b + c) [1 {2(c + a) – 0}]
= 2(a+b)(b + c) (c + a) = RHS

Question 12.
Using properties of determinants, prove that
\(\left|\begin{array}{ccc}
a^{2}+2 a & 2 a+1 & 1 \\
2 a+1 & a+2 & 1 \\
3 & 3 & 1
\end{array}\right|\) = (a – 1) ³
Answer:

On expanding along C ₃ , we get
LHS = (a – 1) ² 1 (a +1 – 2)
= (a – 1) ² (a – 1) = (a – 1) ³
= RHS
Hence Proved.

Question 13.
Using properties of determinants, prove that (CBSE 2018)
\(\left|\begin{array}{ccc}
1 & 1 & 1+3 x \\
1+3 y & 1 & 1 \\
1 & 1+3 z & 1
\end{array}\right|\) = 9 (3xyz + xy + yz + zx).
Answer:
Let Δ = \(\left|\begin{array}{ccc}
1 & 1 & 1+3 x \\
1+3 y & 1 & 1 \\
1 & 1+3 z & 1
\end{array}\right|\)
On taking common x from R ₁ , ,y from R ₂ and z from R ₃ we get

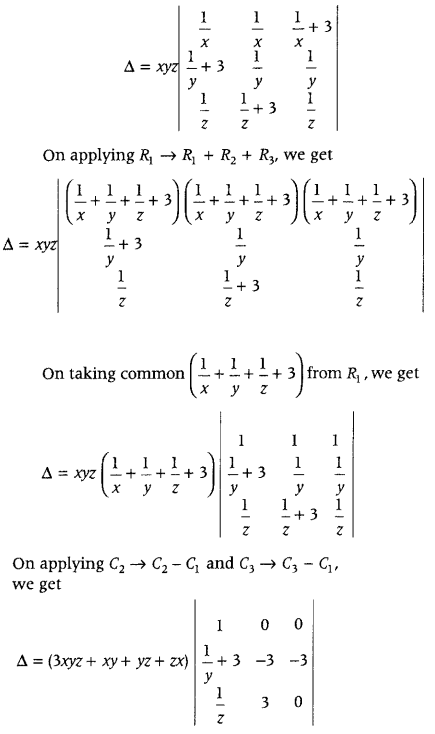
= (3xyz + xy + yz + zx)[1 – {0 – (-9)}]
= 9(3xy + xy + yz + zx)
= RHS
Hence Proved.

Question 14.
Using properties of determinants, prove that (CBSE 2018C)
\(\left|\begin{array}{ccc}
5 a & -2 a+b & -2 a+c \\
-2 b+a & 5 b & -2 b+c \\
-2 c+a & -2 c+b & 5 c
\end{array}\right|\) = 12 (a + b + c) (ab + bc + ca).
Answer:

[Applying R ₂ → R ₂ – R ₁ and R ₃ → R ₃ – R ₁ ]
Expanding along C ₁ , we get
= (a + b + c)[1{(4b + 2a)(4c + 2a) – (-2b + 2a)(-2c + 2a) = 0 = 0]
= (a + b + c)[4{(2b + a)(2c – a) – (-b + a)(-c + a)]
(a + b + c)4[{4bc + 2ab + 2ac + a ² – (bc – ab – ac + a ² )
= 4(a + b + c)[3bc + 3ab + 3ac]
= 12(a + b + c)(ab + bc + ca0
Hence Proved.

Question 15.
Using properties of determinants, prove that (Delhi 2017: All India 2017)
\(\left|\begin{array}{ccc}
x & x+y & x+2 y \\
x+2 y & x & x+y \\
x+y & x+2 y & x
\end{array}\right|\) = 9y ² (x + y).
Answer:

Now, on expanding along Rv we get
LHS = 3 (x + y) -1 . [(- 2y) . (-y) – (y) . <-y>]
= 3 (x + y) (2y ² + y ² )
= 3 (x + y) (3y ² )
= 9y ² (x + y) = RHS
Hence proved.

Question 16.
If f(x) = \(\left|\begin{array}{ccc}
a & -1 & 0 \\
a x & a & -1 \\
a x^{2} & a x & a
\end{array}\right|\) using properties of determinants, find the value of f(2x) – f(x). (Delhi 2015)
Answer:
First, expand the determinants by using properties and then determine the required result.

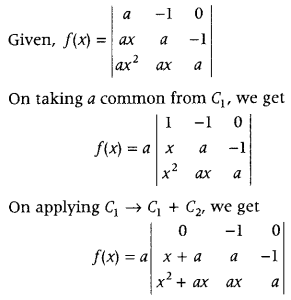
Now, on expanding along R ₁ , we get
f(x) = a[1 { a(x + a) + 1 (x ² + ax)}]
= a (ax + a ² + x ² + ax)
= a (x ² + 2ax + a ² )
= a(x + a) ²

f(2x) = a(2x + a) ²
Now, f(2x) – f(x) = a(2x + a) ² – a(x + a)
= a[(2x + a) ² – (x + a) ² ]
= a[(2x + a + x + a) (2x + a – x – a)] [∵ (a + b) (a – b) = a ² – b ² ]
= a[(3x + 2a) (x)]
= x(3x + 2a) a

Question 17.
Using properties of determinants, prove that (Foreign 2015, 2009)
\(\left|\begin{array}{ccc}
1 & a & a^{2} \\
a^{2} & 1 & a \\
a & a^{2} & 1
\end{array}\right|\) = (1 – a ³ ) ²
Or
Using properties of determinants, prove the following.
\(\left|\begin{array}{ccc}
1 & x & x^{2} \\
x^{2} & 1 & x \\
x & x^{2} & 1
\end{array}\right|\) = (1 – x ³ ) ²
Answer:

On taking (1 – a) common from C ₁ , and C ₂ respectively, we get
LHS = (1 + a + a ² ) (1 – a) ² \(\left|\begin{array}{cc}
1 & a \\
-a & 1+a
\end{array}\right|\)
= (1 + a + a ² ) (1 – a) ² (1 + a + a ² )
= {(1 + a + a ² )(1 – a)} ²
= (1 – a ³ ) ²
= RHS
[∵ (a ² + b ² + ab){a – b) = a ³ – b ³ ]

Question 18.
Using properties of determinants, prove that (All Indio 2015; Foreign 2014)
\(\left|\begin{array}{ccc}
a^{2} & b c & a c+c^{2} \\
a^{2}+a b & b^{2} & a c \\
a b & b^{2}+b c & c^{2}
\end{array}\right|\) = 4a ² b ² bc ²
Answer:

On expanding along C ₁ , we get
LHS = abc [2b {c {a – c) + c(a + c)}]
= 2(ab ² c) (2ac)
= 4a ² b ² c ² = RHS
Hence proved.

Question 19.
Using properties of determinants, solve the following for x. (All Indio 2015C, 2011)
\(\left|\begin{array}{lll}
a+x & a-x & a-x \\
a-x & a+x & a-x \\
a-x & a-x & a+x
\end{array}\right|\) = 0
Answer:

On Expanding along C ₁ , we get
(3a – x).1.\(\left|\begin{array}{cc}
2 x & 0 \\
0 & 2 x
\end{array}\right|\) = 0
⇒ (3a – x).2x.2x = 0
⇒ 4x ² (3a – x) = 0
∴ x = 0,3a

Question 20.
Using properties of determinants, prove that (Delhi 2015C)
\(\left|\begin{array}{lll}
(a+1)(a+2) & a+2 & 1 \\
(a+2)(a+3) & a+3 & 1 \\
(a+3)(a+4) & a+4 & 1
\end{array}\right|\) = 2
Answer:

Now, on expanding along C3, we get
LHS = 4 (a + 2) – 4a – 10= 4a + 8 – 4a – 10
= – 2 = RHS
Hence proved.

Question 21.
Prove the following, using properties of determinants.
\(\left|\begin{array}{ccc}
a+b+2 c & a & b \\
c & b+c+2 a & b \\
c & a & c+a+2 b
\end{array}\right|\) = 2(a + b + c) ³ [Delhi 2014]
Or
Prove, using properties of determinants
\(\left|\begin{array}{ccc}
x+y+2 z & x & y \\
z & y+z+2 x & y \\
z & x & z+x+2 y
\end{array}\right|\) = 2(x + y + z) ³ . (F0reiqn 2011; All India 2009C, 2008)
Answer:

On taking(a + b + c) common from R ₂ and R ₃ we get
LHS = 2 (a+b + c) ³ \(\left|\begin{array}{lll}
1 & a & b \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right|\)
On expanding along R ₃ , we get
LHS = 2(a + b + c) ³ (1 – 0)
= 2(a + b + c) ³ = RHS
Hence Proved
Or
Same as Above.

Question 22.
Using properties of determinants, prove that (Delhi 2014)
\(\left|\begin{array}{ccc}
x^{2}+1 & x y & x z \\
x y & y^{2}+1 & y z \\
x z & y z & z^{2}+1
\end{array}\right|\) = 1 + x ² + y ² + z ² .
Or
Prove, using properties of determinants (All India 2011C; ForeIgn 2009)
\(\left|\begin{array}{ccc}
a^{2}+1 & a b & a c \\
a b & b^{2}+1 & b c \\
c a & c b & c^{2}+1
\end{array}\right|\) = 1 + a ² + b ² + c ² .
Answer:
To Prove

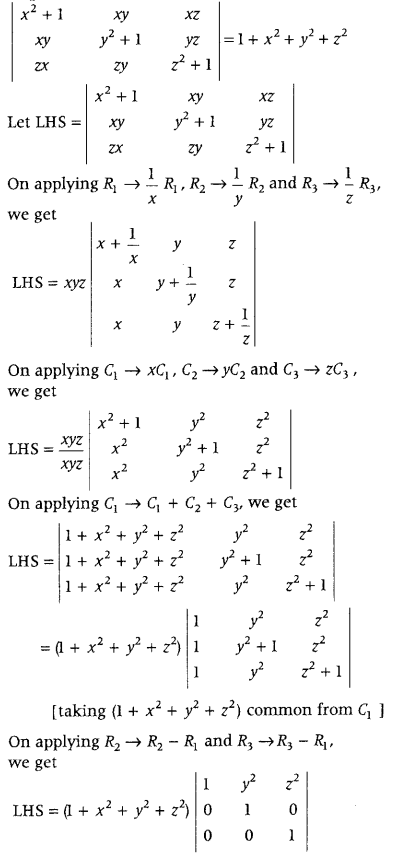
On expanding along C ₁ , we get
LHS = (1 + x ² + y ² + z ² )[1 (1 – 0)]
= 1 + x ² + y ² + z ² = RHS
Hence proved.

Note: If we divide any row (or column) by a non-zero constant k, then we have to multiply the determinant by k.
or
Same as Above

Question 23.
Using properties of determinants, prove that (Delhi 2014)
\(\left|\begin{array}{ccc}
2 y & y-z-x & 2 y \\
2 z & 2 z & z-x-y \\
x-y-z & 2 x & 2 x
\end{array}\right|\) = (x + y + z) ³
Answer:

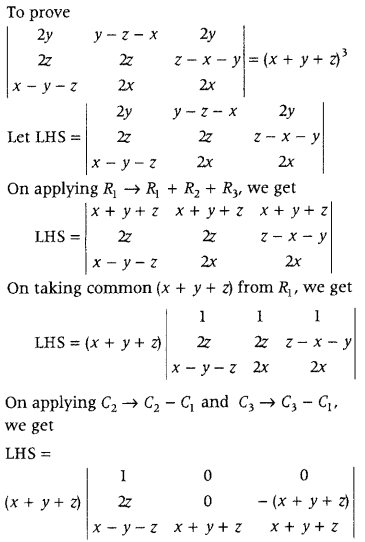
Now, on expanding along we get
LHS = (x + y + z) 1 . [0 + (x + y + z) ² ]
= (x + y+ z) ³ = RHS
Hence Proved.

Question 24.
Using properties of determinants, prove that (All India 2014, 2010C)
\(\left|\begin{array}{ccc}
b+c & c+a & a+b \\
q+r & r+p & p+q \\
y+z & z+x & x+y
\end{array}\right|\) = 2\(\left|\begin{array}{lll}
a & b & c \\
p & q & r \\
x & y & z
\end{array}\right|\)
Answer:
To Prove

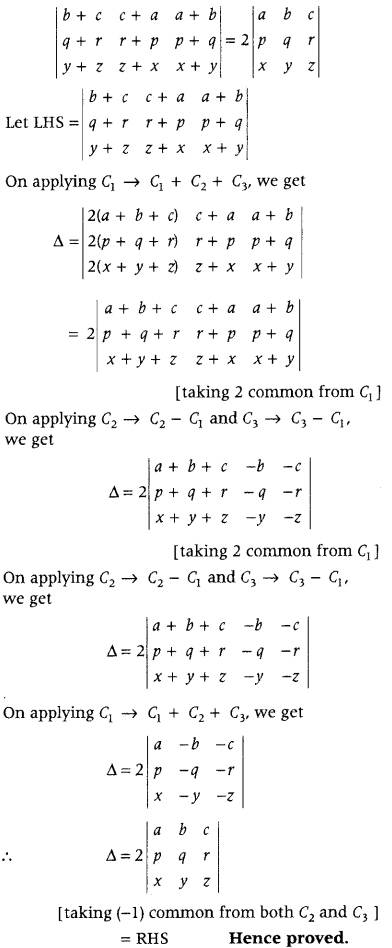
Question 25.
Using properties of determinants, prove that
\(\left|\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right|\) = abc + bc + ca + ab (All India 2014, 2009)
Answer:
T0 Prove

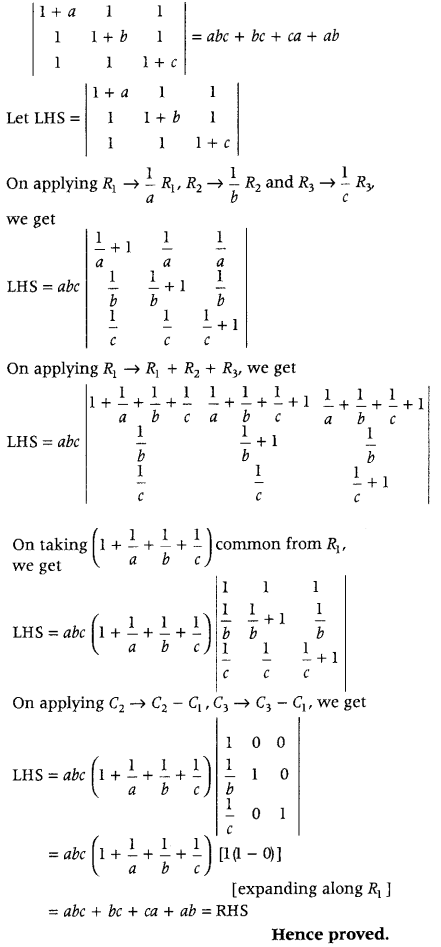
Question 26.
Using properties of determinants, prove that
\(\left|\begin{array}{ccc}
x+y & x & x \\
5 x+4 y & 4 x & 2 x \\
10 x+8 y & 8 x & 3 x
\end{array}\right|\) = x ³ (All India 2014, 2009)
Answer:

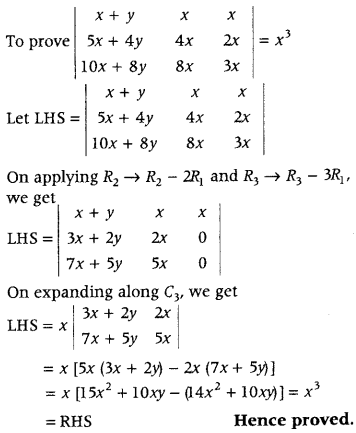
Question 27.
Using properties of determinants, prove that
\(\left|\begin{array}{ccc}
a+x & y & z \\
x & a+y & z \\
x & y & a+z
\end{array}\right|\) = a ² (a + x + y + z) (F0reign 2014)
Answer:
First, we apply the operation C ₁ → C ₁ + C ₂ + C ₃ and then take (a + x + y + z) common factor from C,. Now, try to make two zeroes in C ₁ , and expand the determinant along C ₁ .
To Prove

On expanding along C ₁ , we get
= (a + x + y + z)[1 (a ² – 0)]
= a ² (a + x + y + z) = RHS
Hence Proved.

Question 28.
Using properties of determinants, prove that
\(\left|\begin{array}{ccc}
x+\lambda & 2 x & 2 x \\
2 x & x+\lambda & 2 x \\
2 x & 2 x & x+\lambda
\end{array}\right|\) = (5x + λ)(λ – x) ² (F0reign 2014)
Or
Using properties of determinants, prove that
\(\left|\begin{array}{ccc}
x+4 & 2 x & 2 x \\
2 x & x+4 & 2 x \\
2 x & 2 x & x+4
\end{array}\right|\) = (5x + 4)(4 – x) ² (Delhi 2011, 2009)
Answer:

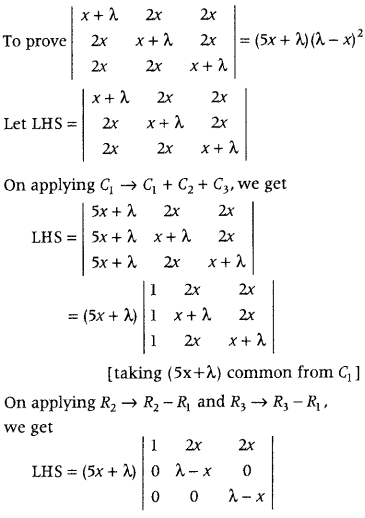
On expanding along C ₁ , we get
LHS = (5x + λ)[1(λ – x) ² – 0]
= (5x + λ)(λ – x) ²
= RHS
Hence Proved
Or
Same as Above.

Question 29.
Using properties of determinants, prove that
\(\left|\begin{array}{lll}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|\) = (a – b)(b – c)(c – a) (bc + ca + ab) (Delhi 2014C)
Answer:


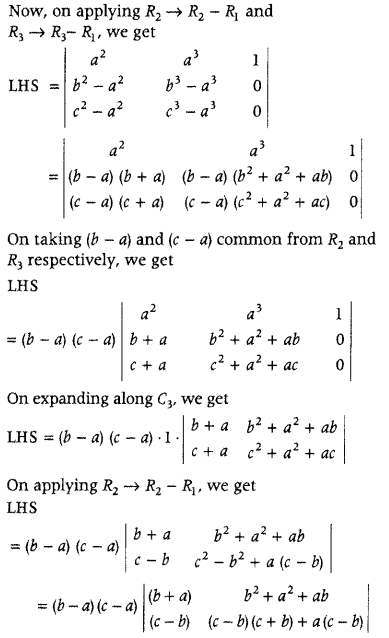
On taking common (c – b) from R ₂ , we get
LHS = (b – a) (c – a) (c – b)
= (b – a) (c – a) (c – b)\(\left|\begin{array}{cc}
b+a & b^{2}+a^{2}+a b \\
1 & c+b+a
\end{array}\right|\)
= (b – a)(c – a)(c – b) [(b + a) (c + b + a) – a ² – b ² – ab]
= (b – a)(c – a)(c – b)[bc + b ² + ab + ac + ab + a ² – a ² – b ² – ab]
= (a – b) (b – c) (c – a) (ab + bc + ca)
= RHS
Hence proved.

Question 30.
Show that Δ = Δ ₁ , where (All India 2014C)

Answer:

Question 31.
Using properties of determinants, prove that (All India 2014C, 2012)
\(\left|\begin{array}{ccc}
b+c & a & a \\
b & c+a & b \\
c & c & a+b
\end{array}\right|\) = 4abc
Answer:
First, apply R ₁ → R ₁ + R ₂ + R ₃ and then take a term common from R ₁ and solve it.

On expanding along R ₁ , we get
LHS = 2{c(ab – 0) – b(0 – ac)}
= 2{abc + abc}
= 4abc
= RHS
Hence Proved

Question 32.
Using properties of determinants, prove that
\(\left|\begin{array}{lll}
1 & a & a^{3} \\
1 & b & b^{3} \\
1 & c & c^{3}
\end{array}\right|\) = (a – b)(b – c)(c – a)(a + b + c). (Delhi 2013C, 2009C)
Answer:

= (b – a)(c – a)[c ² + a ² + ac – (b ² + a ² + ab)] [expanding along C ₁ ]
= (b – a) (c – a) [c ² – b ² + ac – ab]
= (b – a)(c – a) [(c – b)(c + b) + a (c – b)]
= (b – a)(c -a)(c – b)(c + b + a)
= (a – b)(b – c)(c – a)(a + b+ c)
= RHS
Hence proved.

Question 33.
Using properties of determinants, prove that (All India 2013C, Delhi 2011C)
\(\left|\begin{array}{ccc}
a & b & c \\
a^{2} & b^{2} & c^{2} \\
b c & c a & a b
\end{array}\right|\) = (a – b)(b – c)(c – a)(ab + bc + ca)
Answer:


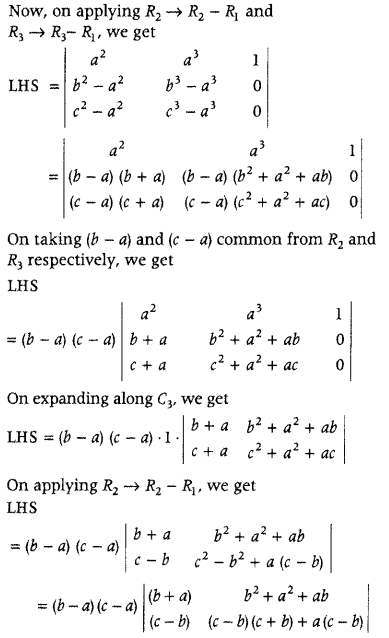
On taking common (c – b) from R ₂ , we get
LHS = (b – a) (c – a) (c – b)
= (b – a) (c – a) (c – b)\(\left|\begin{array}{cc}
b+a & b^{2}+a^{2}+a b \\
1 & c+b+a
\end{array}\right|\)
= (b – a)(c – a)(c – b) [(b + a) (c + b + a) – a ² – b ² – ab]
= (b – a)(c – a)(c – b)[bc + b ² + ab + ac + ab + a ² – a ² – b ² – ab]
= (a – b) (b – c) (c – a) (ab + bc + ca)
= RHS
but replace row operations by column operations and column operations by row operations otherwise write LHS
\(\left|\begin{array}{ccc}
a & b & c \\
a^{2} & b^{2} & c^{2} \\
b c & c a & a b
\end{array}\right|=\left|\begin{array}{ccc}
a & a^{2} & b c \\
b & b^{2} & c a \\
c & c^{2} & a b
\end{array}\right|\)

Question 34.
Using properties of determinants, prove that (Delhi 2012)

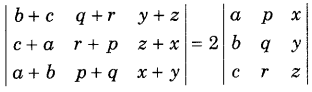
Answer:
To Prove

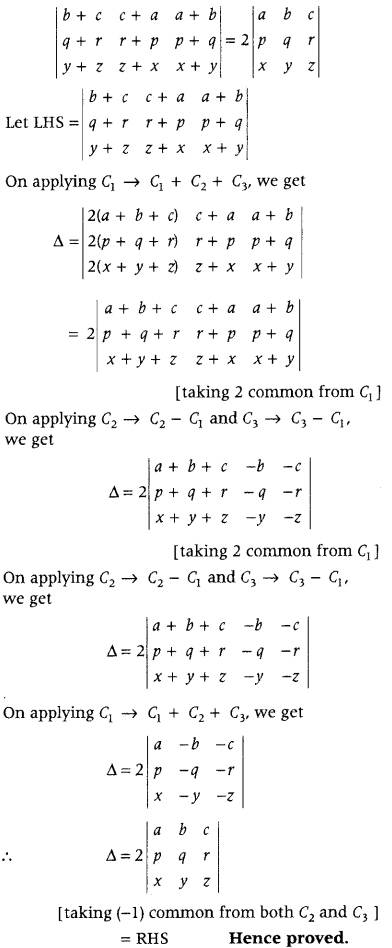
but replace column operations by row operations. Otherwise write

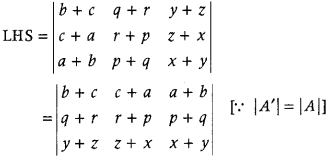
Question 35.
Using properties of determinants, prove the following (Delhi 2012, 2011C)
\(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^{3} & b^{3} & c^{3}
\end{array}\right|\) = (a – b)(b – c)(c – a)(a + b + c)
Answer:

= (b – a)(c – a)[c ² + a ² + ac – (b ² + a ² + ab)] [expanding along C ₁ ]
= (b – a) (c – a) [c ² – b ² + ac – ab]
= (b – a)(c – a) [(c – b)(c + b) + a (c – b)]
= (b – a)(c -a)(c – b)(c + b + a)
= (a – b)(b – c)(c – a)(a + b+ c)
= RHS
but replace column operations by row operations and row operations by column operations. Otherwise write
LHS = \(\left|\begin{array}{ccc}
1 & 1 & 1 \\
a & b & c \\
a^{3} & b^{3} & c^{3}
\end{array}\right|=\left|\begin{array}{lll}
1 & a & a^{3} \\
1 & b & b^{3} \\
1 & c & c^{3}
\end{array}\right|\)

Question 36.
Using properties of determinants, prove the following (Delhi 2019, 2012C, 2009)
\(\left|\begin{array}{ccc}
a & b & c \\
a-b & b-c & c-a \\
b+c & c+a & a+b
\end{array}\right|\) = a ³ + b ³ + c ³ – 3abc
Answer:
To Prove

On expanding along R ₁ , we get
LHS = (a + b+ c).1.{(2b – a – c)(a – c) – (a – b)(b +c – 2a)}
= (a + b + c){2ab – a ² – ac – 2bc + ac + c ² – ab – ac + 2a ² + b ² + bc – 2ab}
=(a+ b + c)(a ² + b ² + c ² – ab – bc – ca)
= a ³ + b ³ + c ³ – 3abc

Question 37.
Using properties of determinants, prove the following (All India 2012C)
\(\left|\begin{array}{ccc}
a & b & c \\
a-b & b-c & c-a \\
b+c & c+a & a+b
\end{array}\right|\) = (a + b + c)(a ² + b ² + c ² )
Answer:

Question 38.
Using properties of determinants, prove that (Delhi 2012C, 2010C, 2008C)
\(\left|\begin{array}{ccc}
\alpha & \beta & \gamma \\
\alpha^{2} & \beta^{2} & \gamma^{2} \\
\beta+\gamma & \gamma+\alpha & \alpha+\beta
\end{array}\right|\) = (α – β)(β – γ)(γ – α)(α + β + γ)
Answer:

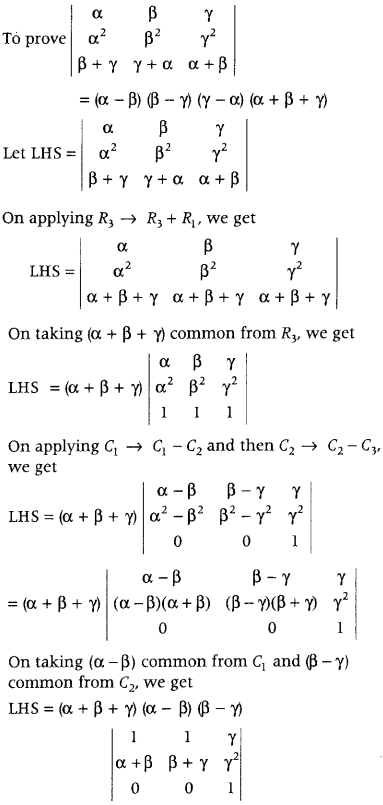
Now, on expanding along R ₃ , we get
LHS = (α + β + γ)(α – β)(β – γ)\(\left|\begin{array}{cc}
1 & 1 \\
\alpha+\beta & \beta+\gamma
\end{array}\right|\)
= (α + β + γ)(α – β)(β – γ)(β + γ – α – β)
= (α – β)(β – γ)( γ – α)(α + β + γ)
= RHS
Hence Proved.

Question 39.
Using properties of determinants, prove that (All India 2012C)
\(\left|\begin{array}{lll}
a^{2} & a^{2}-(b-c)^{2} & b c \\
b^{2} & b^{2}-(c-a)^{2} & c a \\
c^{2} & c^{2}-(a-b)^{2} & a b
\end{array}\right|\) = (a – b)(b – c)(c – a)(a + b + c)(a ² + b ² + c ² )
Answer:

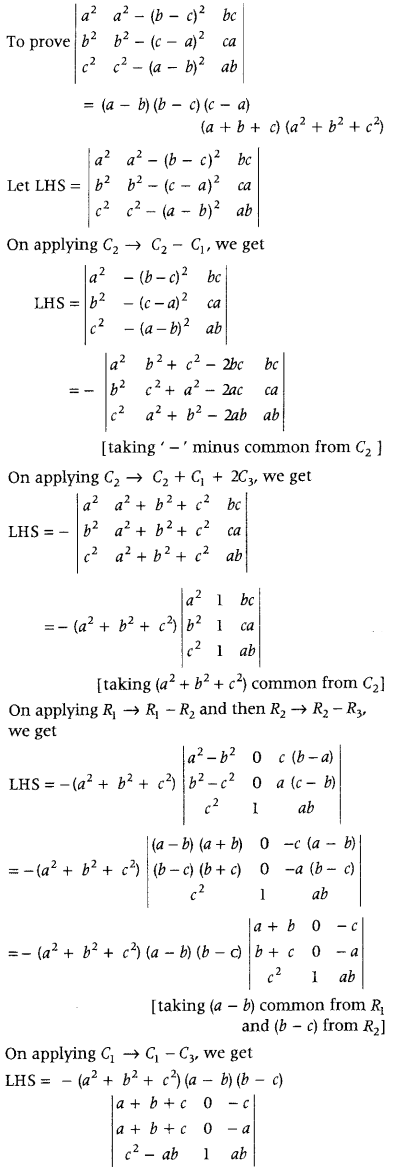
Now, on Expanding along C ₂ , we get
LHS = (a ² + b ² + c ² )(a – b)(b – c)(-1) ³⁺² (a + b + c)(-a + c)
= (a – b)(b – c)(c – a)(a + b + c)(a ² + b ² +c ² )
= RHS
Hence Proved.

Question 40.
Using properties of determinants, prove that (Delhi 2011; All India 2011C)
\(\left|\begin{array}{ccc}
-a^{2} & a b & a c \\
b a & -b^{2} & b c \\
c a & c b & -c^{2}
\end{array}\right|\) = 4a ² b ² c ²
Answer:

Question 41.
Using properties of determinants, prove that (Delhi 2011; All India 2011C)
\(\left|\begin{array}{ccc}
x & y & z \\
x^{2} & y^{2} & z^{2} \\
x^{3} & y^{3} & z^{3}
\end{array}\right|\) = xyz(x – y)(y – z)(z – x)
Answer:
To Prove

On taking (x – y) common from C ₁ and (y – z) from C ₂ , we get
LHS = xyz(x – y)(y – z)\(\left|\begin{array}{cc}
1 & 1 \\
x+y & y+z
\end{array}\right|\)
= xyz(x – y)(y – z)[(y + z) – (x + y)]
= xyz(x – y)(y – z)(z – x)
= RHS
Hence Proved.

Question 42.
Using properties of determinants, solve the following for x. (Delhi 2011, 2010C)

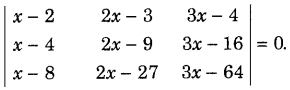
Answer:
First, apply some properties, so that when we expand the determinant, it is easy to simplify.
Given,

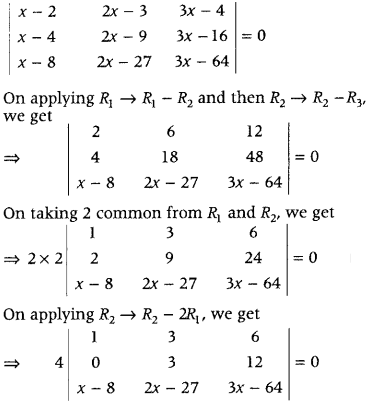
On expanding along Cj, we get
⇒ 4 [3 (3x – 64) – 12 (2x – 27) + (x – 8) (3 × 2 – 3 × 6)] = 0
⇒ 4[9x – 192 – 24x + 324 + (x – 8)18] = 0
⇒ 4(3x – 12) = 0
⇒ 3x = 12
∴ x = 4

Question 43.
Using properties of determinants, solve the following for x. (All India 2011)

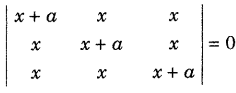
Answer:

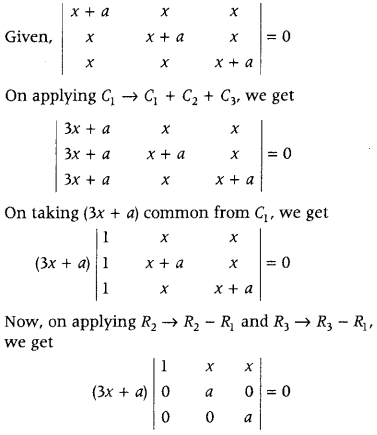
On expanding along C ₁ , we get
(3x + a)[1(a × a – 0)] = 0
⇒ a ² (3x + a) = 0
∴ x = \(-\frac{a}{3}\)

Question 44.
Prove, using properties of determinants (Foreign 2011)

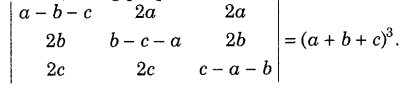
Answer:

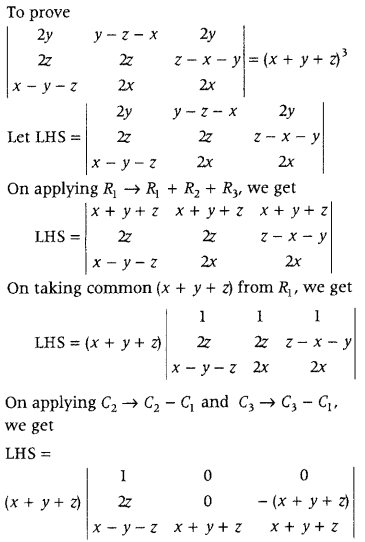
Now, on expanding along we get
LHS = (x + y + z) 1 . [0 + (x + y + z) ² ]
= (x + y+ z) ³ = RHS
Hence Proved.

Question 45.
Prove, using properties of determinants (Foreign 2011)

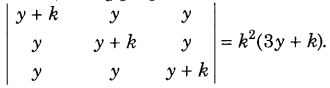
Answer:
First, we apply the operation C ₁ → C ₁ + C ₂ + C ₃ and then take (a + x + y + z) common factor from C,. Now, try to make two zeroes in C ₁ , and expand the determinant along C ₁ .
To Prove

On expanding along C ₁ , we get
= (a + x + y + z)[1 (a ² – 0)]
= a ² (a + x + y + z) = RHS
Hence Proved.

Question 46.
Prove that

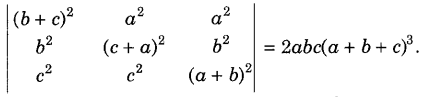
Answer:

On expanding along R1, we get
LHS = (a + b + c) ² [2bc(a ² + ab + ac + bc – bc)]
= (a + b + c) ² [2bc (a ² + ab + ac)]
= (a + b + c) ² .2abc(a + b+c)
= 2abc(a + b + c) ³ = RHS
Hence Proved.

Question 47.
Prove that

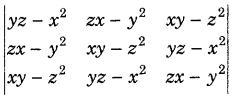
is divisible by (x + y + z) and hence find the quotient. (Delhi 2016)
Answer:

On expanding along R ₁ , we get = (x + y + z) ² (xy + xz + yz – x ² – y ² – z ² ) [1{(y – z)(z – y) – (y – x)(z – x)}]
= (x + y + z) ² (xy + xz + yz – x ² – y ² – z ² ) x [-(y ² + z ² – 2yz) – (yz – xy – xz + x ² )]
= (x + y + z) ² (xy + xz + yz – x ² – y ² – z ² ) x [yz + xy + xz – x ² – y ² – z ² ]
⇒ Δ = (x + y + z) ² (xy + xz + yz – x ² – y ² – z ² ) ²
Here, we see that A is a multiple of x + y + z.
So, it is divisible by x + y + z.
Hence, the quotient is (x + y + z)(xy + xz + yz + x ² – y ² – z ² ) ²

Question 48.
Using properties of determinants, prove that (All India 2015)

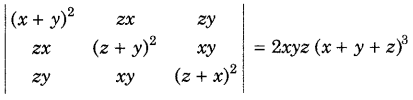
Or
Using properties of determinants, show the following (Delhi 2010)

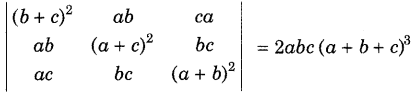
Answer:

Question 49.
Using properties of determinants, show that ΔABC is isosceles, if (All India 2016)

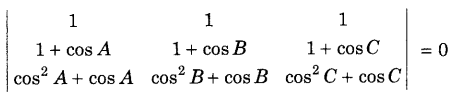
Answer:

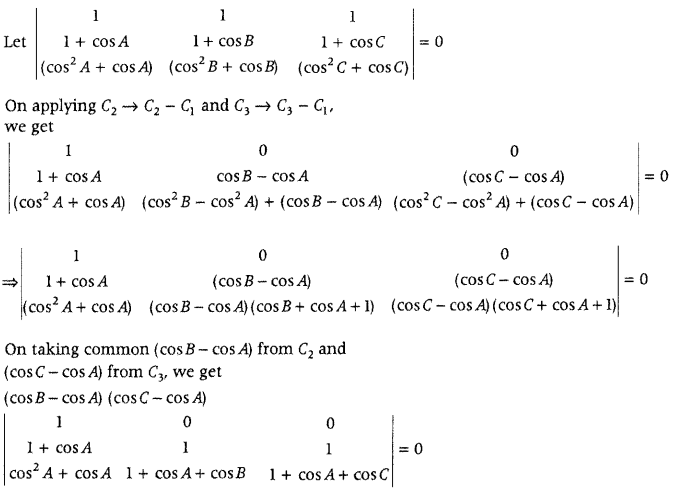
On expanding along R ₁ , we get (cosB – cos A) (cos C- cos A)[1 + cosA + cos C – 1 – cos A – cosB] = 0
⇒ (cosB – cosA) (cosC – cosA) (cosC – cosB) = 0
cosB = cosA or cosC=cosA
or cosC = cosB
⇒ ∠B = ∠A
or ∠C = ∠A
or ∠C = ∠B
ΔABC is isosceles.

Question 50.
If a, b and c are all non-zero and

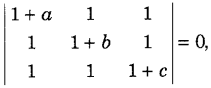
then, prove that \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) + 1 = 0 (Foreign 2016)
Answer:
Consider \(\left|\begin{array}{ccc}
1+a & 1 & 1 \\
1 & 1+b & 1 \\
1 & 1 & 1+c
\end{array}\right|\) = 0 and
T0 Prove

From this, we get abc(1 + \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)) = 0
1 + \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) = 0
[∵ a, b and c are all non-zero constants]

Question 51.
If a, b, c are positive and unequal, show that the following determinant is negative. (All India 2010)
Δ = \(\left|\begin{array}{lll}
a & b & c \\
b & c & a \\
c & a & b
\end{array}\right|\)
Answer:

On expanding along R ₁ , we get
A = (a + b + c) [- (b – c) ² – (a – b) (a – c)]
= (a + b + c) [- (b ² + c ² – 2bc) – (a ² – ac – ab + bc)]
= (a + b + c)[-b ² – c ² + 2bc – a ² + ac +ab – bc]
= (a + b + c) (ab + bc + ca – a ² – b ² – c ² )
= – (a + b + c)(a ² + b ² + c ² – ab – bc – ca)
= \(\frac{1}{2}\) (a + b + c) (2a ² + 2b ² + 2c ² – 2ab – 2bc – 2ca) [multiplying and divide by 2]
= \(\frac{1}{2}\) (a + b+ c){(a – b) ² + (b – c) ² + (c – a) ² } < 0 [∵ a, b, c > 0 and a ≠ b ≠ c]
Hence Proved.

Question 52.
Using properties of determinants, prove the following. (All India 2010)
\(\left|\begin{array}{lll}
x & x^{2} & 1+p x^{3} \\
y & y^{2} & 1+p y^{3} \\
z & z^{2} & 1+p z^{3}
\end{array}\right|\) = (1 + pxyz) (x – y)(y- z) (z – x)
Answer:
To Prove \(\left|\begin{array}{lll}
x & x^{2} & 1+p x^{3} \\
y & y^{2} & 1+p y^{3} \\
z & z^{2} & 1+p z^{3}
\end{array}\right|\)
= (1 + pxyz)(x – y)(y – z)(z – x)

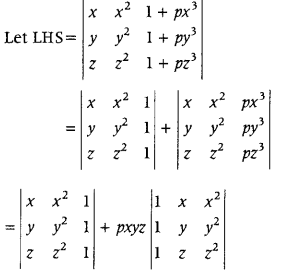
[taking common p from C ₃ , x from R ₁ y from R ₂ and z from R ₃ in 2nd determinant]
On interchanging C ₁ and C ₃ is 1st determinant, we get

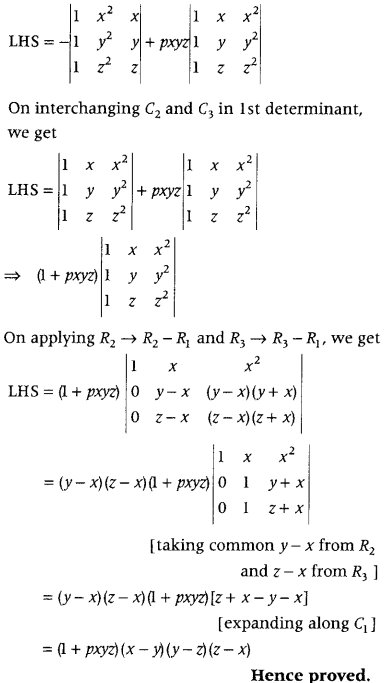
Adjoint and Inverse of a Matrix

Question 1.
If for any 2 × 2 square matrix A, A(adj A) = \(\left[\begin{array}{ll}
8 & 0 \\
0 & 8
\end{array}\right]\), then write the value of |A|. (All India 2017)
Answer:
Given, A(adjA) = \(\left[\begin{array}{ll}
8 & 0 \\
0 & 8
\end{array}\right]\)
⇒ |A(adiA)| = \(\left|\begin{array}{ll}
8 & 0 \\
0 & 8
\end{array}\right|\)
⇒ |A||adi(A)| = 64 – 0
⇒ |A| |A| ² = 64 [∵ |adi A| = |A| ^n-1 ]
⇒ |A| ² = 64 ⇒ |A| = ±8

Question 2.
For what values of k the system of linear equations
x + y + z = 2
2x + y – z = 3
3x + 2y + kz = 4 has a unique solutions? (All India 2016)
Answer:
Given, system of linear equations is
x + y + z = 2
2x + y – z = 3
3x + 2y + kz = 4
It can be written in matrix form as
AX = B
Where, A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
2 & 1 & -1 \\
3 & 2 & k
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) and B = \(\left[\begin{array}{l}
2 \\
3 \\
4
\end{array}\right]\)

The condition for the system of linear equations has a unique solution, is
A ≠ 0
∴ \(\left|\begin{array}{rrr}
1 & 1 & 1 \\
2 & 1 & -1 \\
3 & 2 & k
\end{array}\right|\) ≠ 0
⇒ 1(k + 2) – 1(2k + 3) + 1(4 – 3) ≠ 0
⇒ k + 2 – 2k – 3 + 1 ≠ 0 ⇒ -k ≠ 0
∴ k ≠ 0
Hence, for a unique solution k should be a non-zero real number.

Question 3.
Find |adj A|, if A = \(\left[\begin{array}{ll}
5 & 2 \\
7 & 3
\end{array}\right]\). (Delhi 2014C)
Answer:
Given, A = \(\left[\begin{array}{ll}
5 & 2 \\
7 & 3
\end{array}\right]\)
Clearly, |A| = \(\left|\begin{array}{ll}
5 & 2 \\
7 & 3
\end{array}\right|\) = 15 – 14 = 1

We know that, if A is a non-singular matrix of order n, then |adj (A) | = |A| ^n-1
∴ |adj(A)| = |A| ^2-1 ⇒ |adj(A) | = (1) ^2-1 = 1

Question 4.
If A is a square matrix of order 3 such that |adjA| = 64,then find |A|. (Delhi 2013C)
Answer:
We know that, for a square matrix of order n,
|adj (A)|= |A| ^n-1
Here, the order of A is 3 × 3 therefore n- 3
Now, |adj (A)| =|A| ^3-1 = |A| ²
Given, |adj (A)|= 64 ⇒ 64 =|A| ²
⇒ (8) ² = |A| ²
⇒ |A| = ±8 [taking square root]

Question 5.
Write A ^-1 for A = \(\left[\begin{array}{ll}
2 & 5 \\
1 & 3
\end{array}\right]\) (Delhi 2011)
Answer:

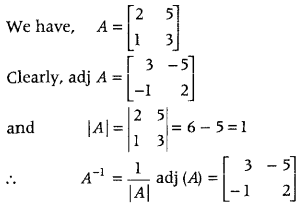
Question 6.
If A = \(\left[\begin{array}{rr}
2 & 3 \\
5 & -2
\end{array}\right]\), then write A in terms of A. (All India 2011)
Answer:

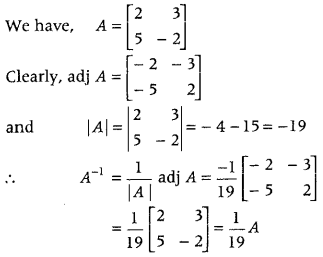
Question 7.
Write the adjoint of the following matrix.
\(\left[\begin{array}{cc}
2 & -1 \\
4 & 3
\end{array}\right]\) (All India 2010)
Answer:
Let A = \(\left[\begin{array}{rr}
2 & -1 \\
4 & 3
\end{array}\right]\), then adj A = \(\left[\begin{array}{ll}
C_{11} & C_{21} \\
C_{12} & C_{22}
\end{array}\right]\), where C _ij denotes the cofactor of a _ij = \(\left[\begin{array}{rr}
3 & 1 \\
-4 & 2
\end{array}\right]\)

Question 8.
If A = \(\left[\begin{array}{rr}
3 & 1 \\
2 & -3
\end{array}\right]\), then find |adjA|. (Delhi 2010C)
Answer:
Given, A = \(\left[\begin{array}{rr}
3 & 1 \\
2 & -3
\end{array}\right]\)
Clearly |A| = \(\left|\begin{array}{ll}
3 & 1 \\
2 & -3
\end{array}\right|\) = -9 – 3 = -11

We know that, if A is a non-singular matrix of order n, then |adj (A) | = |A| ^n-1
∴ |adj(A)| = |A| ^2-1 ⇒ |adj(A) | = (-11) ^2-1 = -11

Question 9.
If |A| = 2 where A is a 2 × 2 matrix, then find |adj A|. (All India 2010C)
Answer:
We know that, for a square matrix of order n,
|adj (A)|= |A| ^n-1
Here, the order of A is 2 × 2 therefore n = 2
Now, |adj (A)| =|A| ^2-1 = |A| ¹
Given, |adj (A)|= 4 ⇒ 4 =|A| ²
⇒ (2) ² = |A| ²
⇒ |A| = ±2 [taking square root]

Question 10.
Given A = \(\left[\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right]\), compute A and show that 2A ^-1 = 9I – A (CBSE 2018)
Answer:

Question 11.
If A= \(\left[\begin{array}{cc}
2 & 3 \\
5 & -2
\end{array}\right]\) be such that A ^-1 = kA,then L —2J find the value of k. (CBSE 2010C)
Answer:
we get, A ^-1 = \(\frac{1}{19}\)A
On comparing with A ^-1 = kA (given), we get
k = \(\frac{1}{19}\)

Question 12.
If A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\), then find (A’) ^-1 . (Delhi 2015)
Answer:
We have, A = \(\left[\begin{array}{ccc}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right]\)
Now, |A| = \(\left|\begin{array}{ccc}
1 & -2 & 3 \\
0 & -1 & 4 \\
-2 & 2 & 1
\end{array}\right|\)
= 1(-1 – 8) + 2 (0 + 8) + 3(0 – 2) [expanding along R ₁ ]
= -9 + 16 – 6 = 1 ≠ 0
So, A is non-singular matrix and its inverse exists.
Cofactors of an element of |A| are given by

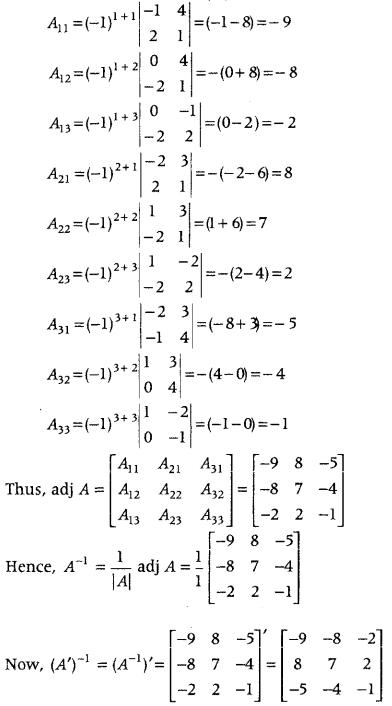
Question 13.
Find the adjoint of the matrix
A = \(\left[\begin{array}{ccc}
-1 & -2 & -2 \\
2 & 1 & -2 \\
2 & -2 & 1
\end{array}\right]\) and hence show that A(adj A) = |A|I ₃ . (All India 2015)
Answer:
Given, \(\left[\begin{array}{ccc}
-1 & -2 & -2 \\
2 & 1 & -2 \\
2 & -2 & 1
\end{array}\right]\)
Let A _ij be the cofactor of an element a _ij of |A|. Then, cofactors of elements of |A| are

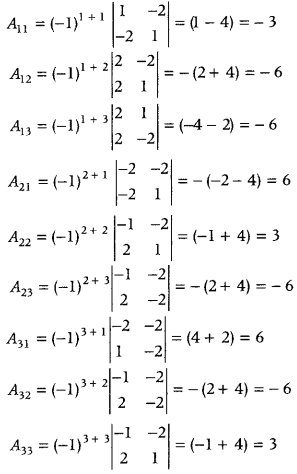
Clearly, the adjoint of the matrix A is given by

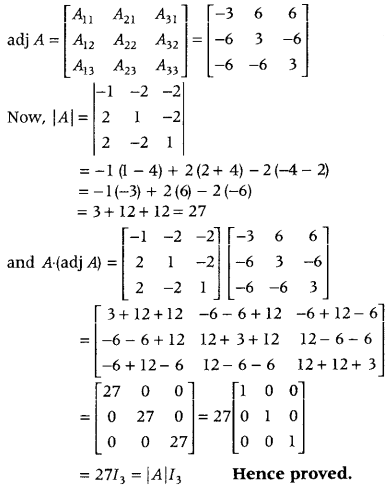
Question 14.
If A = \(\left[\begin{array}{cc}
2 & -1 \\
-1 & 2
\end{array}\right]\) and lis the identity matrix of order 2, then show that A ² = 4A – 3I. Hence, find A ^-1 . (Foreign 2015)
Answer:

So, A is non-singular matrix and its inverse exists.
Now, pre-multiplying both sides of Eq. (iii) by A ^-1 , we get
A ^-1 .A ² = A ^-1 .(4A – 3I)
⇒ (A ^-1 .A) A = 4A ^-1 A – 3A ^-1 .I
⇒ IA = 4I – 3A ^-1 [∵ A.A ^-1 = I = A ^-1 A and A ^-1 I = A ^-1 ]
⇒ A = 4I – 3A ^-1 [∵ IA = A = AI]
⇒ 3A ^-1 = 4I – A

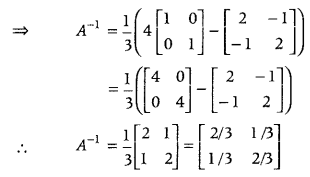
Question 15.
If A = \(\left[\begin{array}{cc}
2 & 3 \\
1 & -4
\end{array}\right]\), B = \(\left[\begin{array}{cc}
1 & -2 \\
-1 & 3
\end{array}\right]\), verify that (AB) ^-1 = B ^-1 A ^-1 . (All India 2015C)
Answer:

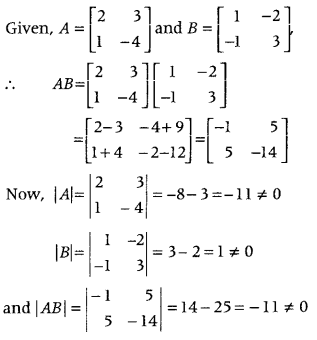
Thus, A, B and AB are non-singular matrices, so their inverse exists.

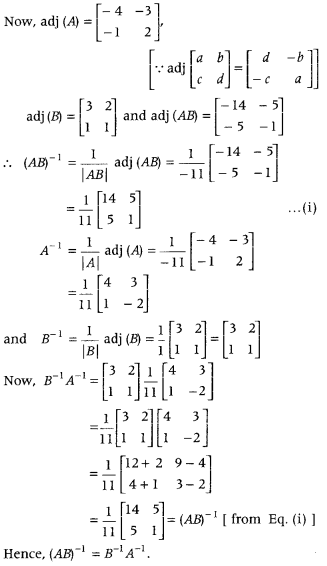
Question 16.
Show that for the matrix A = \(\left[\begin{array}{rrr}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right]\), A ³ – 6A ² + 5A + 11I = O. Hence, find A ^-1 . (All India 2019)
Answer:

⇒ A ³ – 6A ² + 5A + 11I ₃ = 0
Now, multiplying both sides by A ^-1 , we get
⇒ A ^-1 (A ³ – 6A ² + 5A + 11I ₂ ) = A ^-1 O [multiplying both sides by A ^-1 ]
⇒ A ² – 6A + 5I + 11A ^-1 = 0

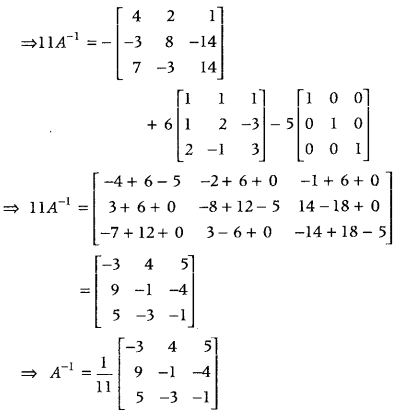
Question 17.
If A = \(\left[\begin{array}{lll}
1 & 3 & 4 \\
2 & 1 & 2 \\
5 & 1 & 1
\end{array}\right]\), find A ^-1 . Hence solve the system of equations
x + 3y + 4z = 8
2x + y + 2z = 5
and 5x + y + z = 7. (All India 2019)
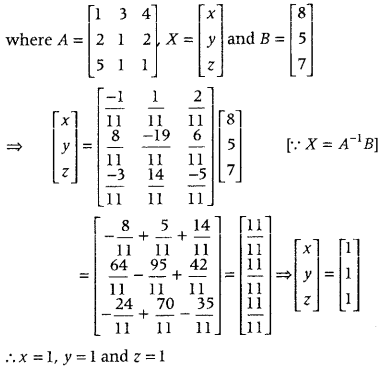
Answer:
Here, |A| = \(\left[\begin{array}{lll}
1 & 3 & 4 \\
2 & 1 & 2 \\
5 & 1 & 1
\end{array}\right]\)
= Id – 2) – 3(2-10) + 4(2-5)
= -1 + 24 – 12 = 11 ≠ 0
Thus, A is invertible.
Clearly, the system has a unique solution given by
X = A ^-1 B.
Now, the cofactors of |A| are
A ₁₁ = -1, A ₁₂ = 8, A ₁₃ = -3
A ₂₁ = 1, A ₂₂ = -19, A ₂₃ = 14
A ₃₁ = 2, A ₃₂ = 6, A ₃₃ = -5

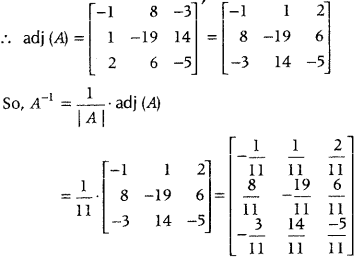
The given equations are
x + 3y + 4z = 8 …….(i)
2x + y + 2z = 5 ………(ii)
and 5x + y + z = 7 ………..(iii)
which can be written in matrix form as AX = B,

Question 18.
If A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 2 \\
3 & 1 & 1
\end{array}\right]\), find A ^-1 . Hence, solve the system of equations x + y + z = 6, x + 2z = 7, 3x + y + z = 12. (Delhi 2019)
Answer:
We have, A = \(\left[\begin{array}{lll}
1 & 1 & 1 \\
1 & 0 & 2 \\
3 & 1 & 1
\end{array}\right]\)
∴ |A| = 1(0 – 2) – 1(1 – 6) + 1(1 – 0)
= -2 + 5 + 1 = 4 ≠ 0
So, A is invertible.

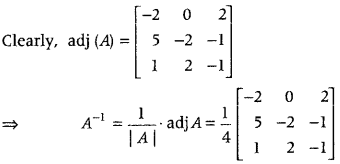
Given, systems of the equations is x + y + z = 6, x + 2z = 7, 3x + y + z = 12,
which can be written in matrix form as AX = B where

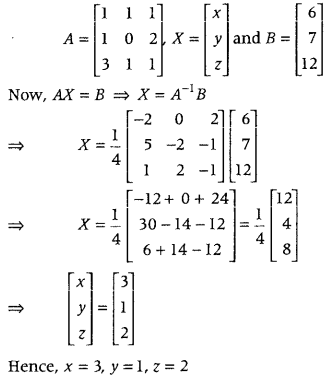
Question 19.
If A =\(\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), A ^-1 . Use it to solve the system of equations 2x – 3y + 5z = 11, 3x + 2y – 4z = -5, x + y – 2z = -3. (CBSE 2018)
Answer:
We have, A = \(\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\)
Here |A| = \(\left|\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right|\)
= 2(- 4 + 4) + 3(- 6 + 4) + 5(3 – 2)
= -6+ 5 = -1 ≠ 0
Thus, A is a non-singular matrix, so A ^-1 exists and the cofactors of elements of |A| are
A ₁₁ = 0, A ₂₁ = -1, A ₃₁ = 2
A ₁₂ = 2, A ₂₂ = -9, A ₃₂ = 23
A ₁₃ = 1, A ₂₃ = -5, A ₃₃ = 13

Question 20.
Given A = \(\left[\begin{array}{lll}
5 & 0 & 4 \\
2 & 3 & 2 \\
1 & 2 & 1
\end{array}\right]\), B ^-1 = \(\left[\begin{array}{lll}
1 & 3 & 3 \\
1 & 4 & 3 \\
1 & 3 & 4
\end{array}\right]\), compute (AB) ^-1 . (CBSE 2018C)
Answer:

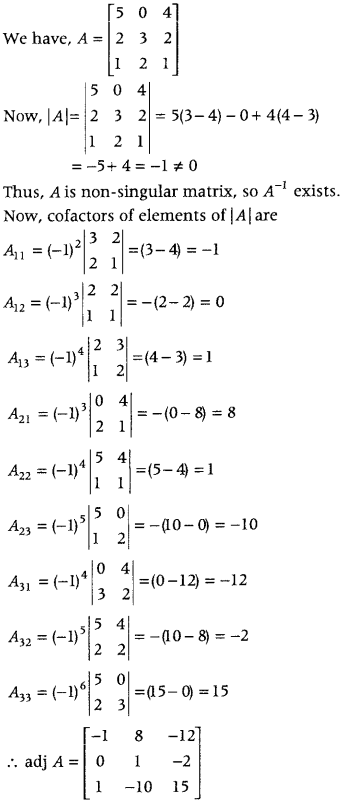
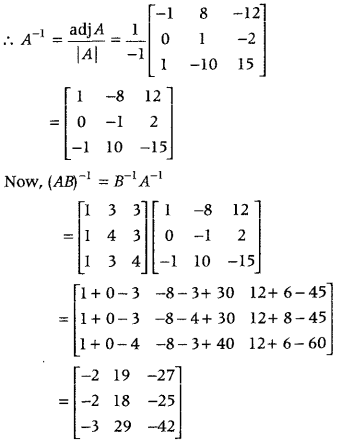
Question 21.
If A = \(\left[\begin{array}{ccc}
2 & 3 & 10 \\
4 & -6 & 5 \\
6 & 9 & -20
\end{array}\right]\), find A ^-1 . Using A ^-1 solve the system of equations
\(\frac{2}{x}+\frac{3}{y}+\frac{10}{z}\) = 2
\(\frac{4}{x}-\frac{6}{y}+\frac{5}{z}\) = 5
and \(\frac{6}{x}+\frac{9}{y}-\frac{20}{z}\) – 4
Answer:
Let \(\frac{1}{x}\) = p, \(\frac{1}{y}\) = q and \(\frac{1}{z}\) = r
Then, the given equations becomes
2p + 3q + 10r =2
4p – 6q + 5r = 5
6p + 9q – 20r = – 4
This system can be written as AX = B, where

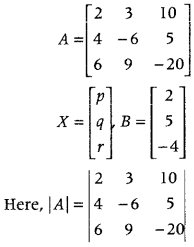
= 2(120 – 45) – 3(-80 – 30) + 10(36 + 36)
= 150 + 330 + 720 = 1200 ≠ 0
Thus, A is non-singular, therefore its inverse exists.
Therefore, the above system has a unique solution given by
X = A ^-1 B
Cofactors of A are
A ₁₁ = 75, A ₂₁ =150, A ₃₁ = 75
A ₁₂ =110, A ₂₂ = -100, A ₃₂ = 30
A ₁₃ = 72, A ₂₃ = 0, A ₃₃ = -24

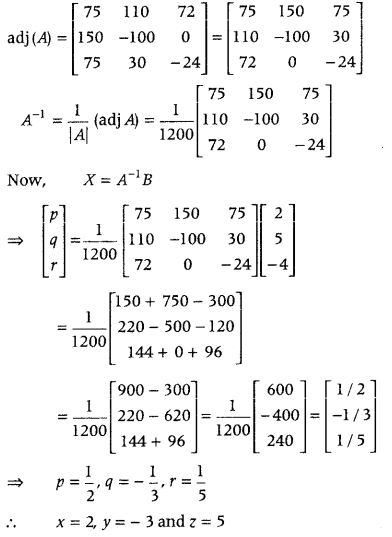
Question 22.
Determine the product of \(\left[\begin{array}{ccc}
-4 & 4 & 4 \\
-7 & 1 & 3 \\
5 & -3 & -1
\end{array}\right]\) \(\left[\begin{array}{ccc}
1 & -1 & 1 \\
1 & -2 & -2 \\
2 & 1 & 3
\end{array}\right]\) and then Use to solve the system of equations
x – y + z = 4
x – 2y – 2z = 9
and 2x + y + 3z = 1. (All India 2017, Delhi 2012C)
Answer:
First, find the product of given matrices and then find the inverse of coefficient matrix by using the obtained product and then by using concept of matrix method, find the values of x, y and z.

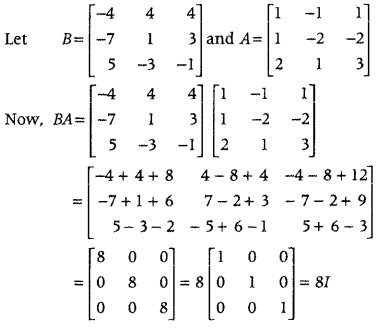
⇒ BA = 8I
⇒ BA(A ^-1 ) = 8I.RA ^-1 [post-multiplying both sides by A’]
⇒ B(AA ^-1 ) = 8I A ^-1
⇒ B = 8A ^-1 [∵ AA ^-1 = I]

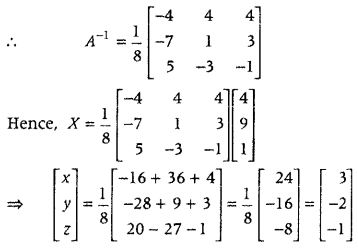
On comparing corresponding elements, we get
x = 3, y = – 2 and z = -1

Question 23.
Use Products \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & -2 & 4
\end{array}\right]\left[\begin{array}{rrr}
-2 & 0 & 1 \\
9 & 2 & -3 \\
6 & 1 & -2
\end{array}\right]\)
to solve the system equations
x – y + 2z = 1
2y – 3z = 1
and 3x – 2y + 4z = 2. (Delhi 2017, Foreign 2011)
Answer:
x = 0, y = 5, z = 3

Question 24.
Using elementary transformations, find the inverse of the matrix A = \(\left[\begin{array}{lll}
8 & 4 & 3 \\
2 & 1 & 1 \\
1 & 2 & 2
\end{array}\right]\) and use it to solve the following system of linear equations:
8x + 4y + 3z = 19
2x + y + z = 5
and x + 2y + 2z = 7. (Delhi 2016)
Answer:


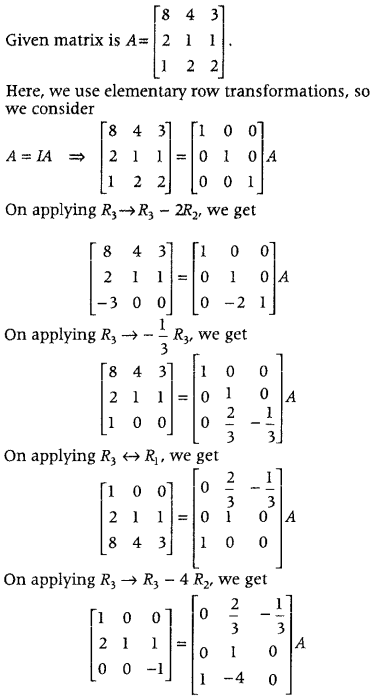
Given system of equations can be written in matrix form as
AX = B,

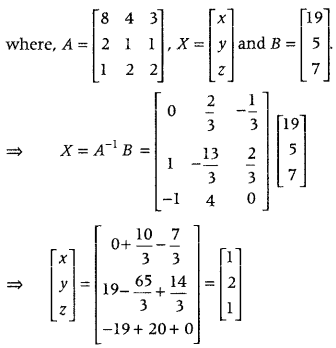
On comparing the corresponding elements, we get
x = 1, y = 2 and z = 1.

Question 25.
If A = \(\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\), find adj A and verify that A(adj A) = (adj A) A = |A|I ₃ . (Foregin 2016)
Answer:
We have, A = \(\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\)
Clearly, the cofactors of elements of |A| are given by
A ₁₁ = Cos α; A ₁₂ = -sin α; A ₁₃ = 0
A ₂₁ = Sin ; A ₂₂ = cos ; A ₂₃ = 0
A ₃₁ = 0; A ₃₂ = 0 and A ₃₃ = 1

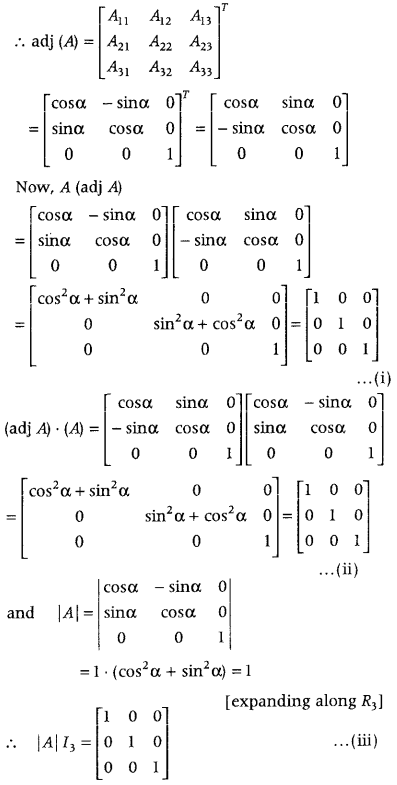
From Eqs. (i), (ii) and (iii), we get
A (adj A) = (adj A) . A = |A|I ₃

Question 26.
A total amount of ₹ 7000 is deposited in three different savings bank accounts with annual interest rates of 5%, 8% and 8 \(\frac{1}{2}\) %, respectively. The total annual interest from these three accounts is ₹ 550. Equal amounts have been deposited in the 5% and 8% savings accounts. Find the amount deposited in each of the three accounts, with the help of matrices. (Delhi 2014C)
Answer:
Let ₹ x, ₹ y and ₹ z be invested in saving bank accounts at the rate of 5%, 8% and 8\(\frac{1}{2}\)%, respectively.
Then, according to given condition we have the following system of equations
x + y + z = 7000 ……….(i)
and \(\frac{5 x}{100}+\frac{8 y}{100}+\frac{17 z}{200}\) = 550 ……….(ii)
⇒ 10x + 16y + 17z = 110000 ……..(iii)
and x – y = 0 ……….(iv)
This system of equations can be written in matrix form as AX = B

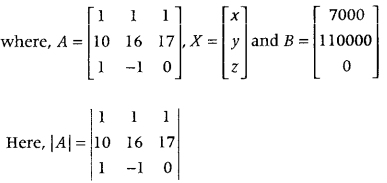
So, A is non-singular matrix and its inverse exists.
Now, cofactors of elements of |A| are


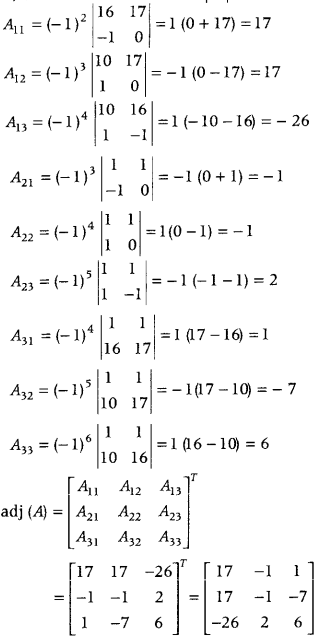
On comparing the corresponding elements, we get x = 1125, y = 1125, z = 4750.
Hence, the amount deposited in each type of account is ₹ 1125, ₹ 1125and ₹ 4750, respectively.

Question 27.
Using matrices, solve the following system of equations.
x – y + 2z = 7
3x + 4y – 5z = – 5
and 2x – y + 3z = 12 (Delhi 2012)
Answer:
First, write the given system of equations in matrix ” form AX = 8. Then, determine the cofactors determinant A and A-1 and then use the relation X = A-1 8, to get the values of x, y and z.
Given, system of equations is
x – y + 2z = 7
3x + 4y – 5z = – 5
and 2x – y + 3z = 12
In matrix form, it can be written as
AX = B ……(i)
Where,

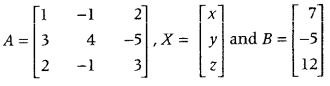
Here, |A| = 1 (12- 5) + 1 (9 + 10) + 2(-3- 8)
= 1 (7) + 1 (19) + 2 (-11)
= 7 + 19 – 22 = 4
⇒ |A| ≠ 0
So, A is non-singular and its inverse exists.
Now, cofactors of elements of |A| are

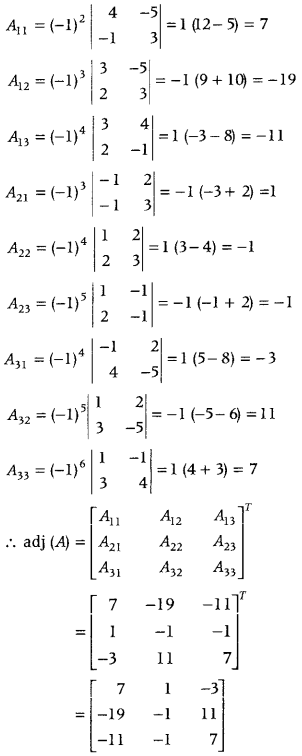
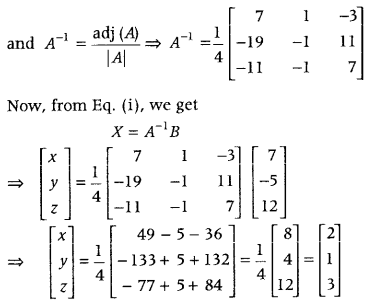
Question 28.
Using matrices, solve the following system of linear equations. x + y – z = 3, 2x + 3y + z = 10 and 3x – y – 7z = 1 (All India 2012; Delhi 2009C)
Answer:
x = 3, y = 1, z = 1

Question 29.
Using matrices, solve the following system of equations.
3x + 4y + 7z = 4,
2x – y + 3z = – 3
and x + 2y – 3z = 8 (All India 2012)
Answer:
x = 1, y = 2, z = -1

Question 30.
Using matrices, solve the following system of equations.
2x + 3y + 3z = 5, x-2y + z = -4 and 3x – y – 2z = 3 (All India 2012)
Answer:
x = 1, y = 2, z = -1

Question 31.
If A = \(\left[\begin{array}{ccc}
1 & 2 & 1 \\
-1 & 1 & 1 \\
1 & -3 & 1
\end{array}\right]\), then find A ^-1 and hence solve the system of equations x + 2y + z = 4, -x + y + z = 0 and x – 3y + z = 4. (Delhi 2012C)
Answer:
A ^-1 = \(\frac{1}{10}\left[\begin{array}{ccc}
4 & -5 & 1 \\
2 & 0 & -2 \\
2 & 5 & 3
\end{array}\right]\)
x = 2, y = 0 and z = 2

Question 32.
Find A ^-1 , where A = \(\left[\begin{array}{ccc}
1 & 2 & -3 \\
2 & 3 & 2 \\
3 & -3 & -4
\end{array}\right]\) solve the system of equations, x + 2y – 3z = – 4 2x + 3y + 2z = 2 and 3x – 3y – 4z = 11. (All India 2012C, 2010,2008)
Answer:
A ^-1 = \(\frac{1}{67}\left[\begin{array}{rrr}
-6 & 17 & 13 \\
14 & 5 & -8 \\
-15 & 9 & -1
\end{array}\right]\)
x = 3, y = -2 and z = 1

Question 33.
Using matrix method, solve the following system of equations. (Delhi 2011)

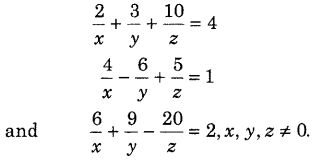
Answer:
First, let \(\frac{1}{x}\) = u, \(\frac{1}{y}\) = v and \(\frac{1}{z}\) = w and then reduce system of equations in terms of u, v and w. Get the values of u, v and w by using matrix method and then find x, y and z from above mentioned substitutions.

The given system of equations is

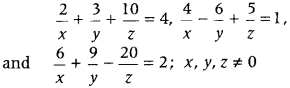
Let \(\frac{1}{x}\) = u, \(\frac{1}{y}\) = v and \(\frac{1}{z}\) = w, then system of x y z equations can be written as
2u + 3v + 10w = 4
4u – 6v + 5w = 1
and 6u + 9v – 20w = 2 …………(i)
Above system of Eqs. (i) can be written in matrix form as AX = B, where

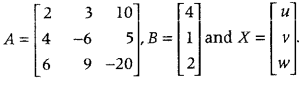
Its solution is given by
X = A ^-1 B …(ii)
Here, |A| = 2 (120 – 45) – 3 (-80 – 30) + 10(36+ 36)
= 2 (75) – 3 (-110) + 10 (72)
= 150 + 330 + 720 = 1200
⇒ |A| = 1200
Since, |A| ≠ 0, so A is non-singular and its inverse exists.
Now, cofactors of elements of |A| are

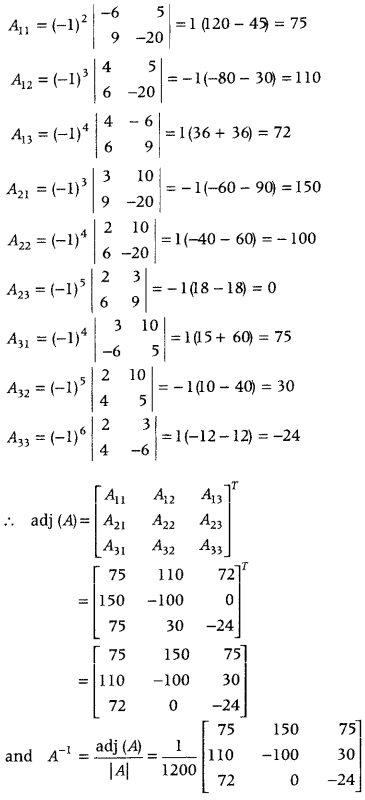
On putting the values X, A ^-1 and B in Eq. (ii), we get

Question 34.
Using matrices, solve the following system of equations.
4x + 3y + 2z = 60
x + 2y + 3z = 45
and 6x + 2y + 3z = 70 (All India 2011)
Answer:
x = 5, y = 8, z = 8

Question 35.
Using matrices, solve the following system of equations. x + 2y + z = 7, x + 3z = 11 and 2x – 3y = 1 (All India 2011; Delhi 2008C)
Answer:
x = 2, y = 1 and z = 3

Question 36.
Using matrices, solve the following system of equations.
x + 2y – 3z = – 4 2x + 3y + 2z = 2 and 3x – 3y – 4z = 11 (All India 2011, 2008)
Answer:
x = 3, y = -2 and z = 1

Question 37.
If A = \(\left[\begin{array}{rrr}
2 & -1 & 1 \\
3 & 0 & -1 \\
2 & 6 & 0
\end{array}\right]\), then find A ^-1 . Using A ^-1 , Solve the following system of equations
2x – y + z = -3, 3x – z = 0 and 2x + 6y – z = 2. (All India 2011C)
Answer:
A ^-1 = \(\frac{1}{32}\left[\begin{array}{rrr}
6 & 6 & 1 \\
-2 & -2 & 5 \\
18 & -14 & 3
\end{array}\right]\); x = \(-\frac{1}{2}\); y = \(\frac{1}{2}\) and z = \(\frac{-3}{2}\)

Question 38.
If A = \(\left[\begin{array}{rrr}
1 & -2 & 1 \\
0 & -1 & 1 \\
2 & 0 & -3
\end{array}\right]\), then find A ^-1 and hence solve the following system of equations
x – 2y + z = 0, -y+z=-2 and 2x – 3z = 10. (All India 2011C)
Answer:
A ^-1 = \(\left[\begin{array}{rrr}
3 & -6 & -1 \\
2 & -5 & -1 \\
2 & -4 & -1
\end{array}\right]\); x = 2, y = 0 and z = -2

Question 39.
If A = \(\left[\begin{array}{rrr}
1 & -2 & 0 \\
2 & 1 & 3 \\
0 & -2 & 1
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
7 & 2 & -6 \\
-2 & 1 & -3 \\
-4 & 2 & 5
\end{array}\right]\) then find AB and hence solve system of equations
x – 2y = 10, 2x + y + 3z = 8 and -2y + z = 7. (Delhi 2011C)
Answer:
AB = 11I, x = 4, y = -3 and z = 1

Question 40.
If A = \(\left[\begin{array}{rrr}
3 & -4 & 2 \\
2 & 3 & 5 \\
1 & 0 & 1
\end{array}\right]\), then find A ^-1 and hence solve the following system of equations
3x – 4y + 2z = – 1, 2x + 3y + 5z = 7 and x + z = 2 (Delhi 2011 C)
Answer:
A ^-1 = \(\frac{1}{10}\left[\begin{array}{rrr}
-6 & 25 & -24 \\
-12 & 40 & -38 \\
10 & -40 & 40
\end{array}\right]\) and x = 3, y = 2, z = -1

Question 41.
If A = \(\left[\begin{array}{rrr}
8 & -4 & 1 \\
10 & 0 & 6 \\
8 & 1 & 6
\end{array}\right]\) then find A ^-1 and hence solve the following system of equations
8x – 4y + 2 = 5 10x + 6z = 4 and 8x + y + 6z = \(\frac{5}{2}\). (All India 2010C)
Answer:
A ^-1 = \(\frac{1}{10}\left[\begin{array}{rrr}
-6 & 25 & -24 \\
-12 & 40 & -38 \\
10 & -40 & 40
\end{array}\right]\) and x = 1, y = \(\frac{1}{2}\), z = -1

Question 42.
If A = \(\left[\begin{array}{rrr}
1 & -1 & 0 \\
2 & 3 & 4 \\
0 & 1 & 2
\end{array}\right]\) and B = \(\left[\begin{array}{rrr}
2 & 2 & -4 \\
-4 & 2 & -4 \\
2 & -1 & 5
\end{array}\right]\) then find AB. Use this to solve the system of equations
x – y = 3, 2x+ 3y + 4z = 17 and y + 2z = 7. (All India 2010C)
Answer:
AB = 6I and x = 2 y = -, z = 4

Question 43.
If A = \(\left[\begin{array}{rrr}
3 & 2 & 1 \\
4 & -1 & 2 \\
7 & 3 & -3
\end{array}\right]\), then find A. Hence solve the following system of equations 3x + 2y + z = 6 4x – y + 2z = 5 and 7x + 3y – 3z = 7. (Delhi 2010C)
Answer:
A ^-1 = \(\frac{1}{62}\left[\begin{array}{ccc}
-3 & 9 & 5 \\
26 & -16 & -2 \\
19 & 5 & -11
\end{array}\right]\) and x = 1, y = 1, z = 1