Probability Class 12 Maths Important Questions Chapter 13

Get access to Class 12 Maths Important Questions Chapter 13 Probability, Probability Class 12 Important Questions with Solutions Previous Year Questions will help the students to score good marks in the board examination.

Probability Class 12 Important Questions with Solutions Previous Year Questions

Question 1.
If P(not A) = 0.7, P(B) = 0.7 and P(B/A) = 0.5, then find P(A/B). (All India 2019)
Answer:

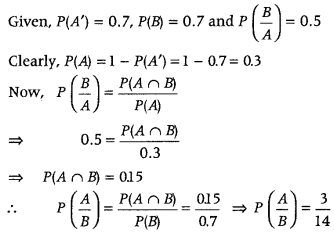
Question 2.
A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event ‘number is even’ and B be the event ‘number is marked red’. Find whether the events A and B are independent or not. (Delhi 2019)
Or
A die, whose faces are marked 1,2, 3 in red and 4, 5, 6 in green , is tossed. Let A be the event “number obtained is even” and B be the event “number obtained is red”. Find if A and B are independent events. (All India 2017)
Answer:
When a die is thrown, the sample space is
S = {1, 2, 3, 4, 5, 6}
⇒ n(S) = 6
Also, A: number is even and B: number is red.
∴ A = {2, 4, 6} and B = {1, 2, 3} and A ∩ B = {2}
⇒ n(A) = 3, n(B) = 3 and n(A ∩ B) = 1

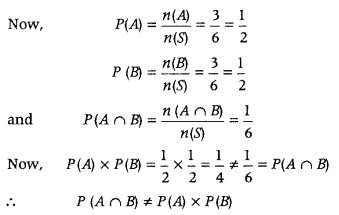
Thus, A and B are not independent events.

Question 3.
A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4. (CBSE 2018)
Answer:
Let us denote the numbers on black die by B ₁ , B ₂ , ……., B ₆ and the numbers on red die by R ₁ , R ₂ , ….., R ₆ .
Then, we get the following sample space.
s = {(B ₁ , R ₁ ) ,(B ₁ , R ₂ ), ……., (B ₁ , R ₆ ), (B ₂ , R ₂ ), ………, (B ₆ , B ₁ ), (B ₆ , B ₂ ), ……., (B ₆ ,R ₆ )
Clearly, n(S) = 36
Now, let A be the event that sum of number obtained on the die is 8 and B be the event that red die shows a number less than 4.
Then, A = {(B ₂ , R ₆ ), (B ₆ ,R ₂ ), (B ₃ ,R ₅ ), (B ₅ ,R ₃ ), (B ₄ ,R ₄ )}
and B = {(B ₁ , R ₁ ), (B ₁ ,R ₂ ), (B ₁ ,R ₃ ), (B ₂ ,R ₁ ), (B ₂ ,R ₂ ), (B ₂ ,R ₃ ) ,…….., (B ₆ ,R ₁ ), (B ₆ ,R ₂ ), (B ₆ ,R ₃ )}
⇒ A ∩ B = {(B ₆ , R ₂ ), (B ₅ , R ₃ )}
Now, required probability,
p\(\left(\frac{A}{B}\right)\) = \(\frac{P(A \cap B)}{P(B)}=\frac{\frac{2}{36}}{\frac{18}{36}}=\frac{2}{18}=\frac{1}{9}\)

Question 4.
Evaluate P(A ∪ B), if 2P (A) = P(B) = \(\frac{5}{13}\) and P(A/ B) = \(\frac{2}{5}\). (CBSE 2018C)
Answer:

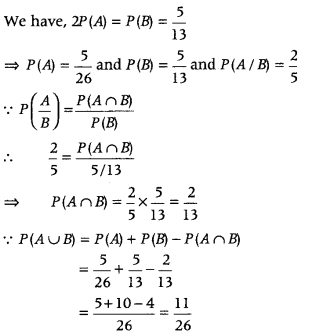
Question 5.
Prove that if E and F are independent events, then the events E and F’ are also independent. (Delhi 2017)
Answer:
Given, E and F are independent events, therefore
⇒ PE( ∩ F) = P(E) P(F) …….. (i)
Now, we have,
P(E ∩ F’) + P(E ∩ F) = P(E)
P(E ∩ F’) = P(E) – P(E ∩ F)
P(E ∩ F’) = P(E) – P(E ) P(F) [using Eq. (i))
P(E ∩ F’) = P(E) [1 – P(F)]
P (E ∩ F’) = P(E ) P(F’)
∴ E and F ‘are also independent events.
Hence proved.

Question 6.
A and B throw a pair of dice alternately. A wins the game, if he gets a total of 7 and B wins the game, if he gets a total of 10. If A starts the game, then find the probability that B wins. (Delhi 2016)
Answer:
Here, n(S) = 6 × 6 = 36
Let A = Event of getting a sum of 7 in pair of dice = {(1, 6), (2, 5), (3, 4), (6, 1), (5, 2), (4, 3)}
⇒ n(A) = 6
and B = Event of getting a sum of 10 in pair of dice = {(4, 6), (5, 5), (6, 4)} ⇒ n(B) = 3

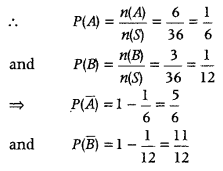
Now, the probability that if A start the game, then B wins
P(B wins) = P(Ā ∩ B) + P (Ā ∩ B̄ ∩ Ā ∩ B) + P(Ā ∩ B̄ ∩ Ā ∩ B̄ ∩ Ā ∩ B) + …
= P(Ā) P(B) + P(Ā)P(B̄)P(Ā)P(B) + P(Ā)P(B̄)P(Ā)P(B̄)P(Ā) P(B) + ….. (1)
[∵ events are independent]

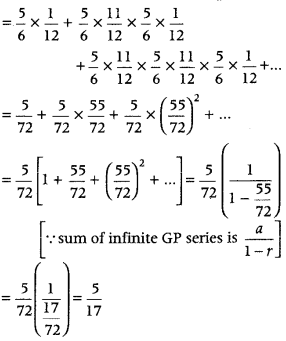
Question 7.
A and B throw a pair of dice alternately, till one of them gets a total of 10 and wins the game. Find their respective probabilities of winning, if A starts first. (All India 2016)
Answer:
Here, n(s) = 6 × 6 = 36
Let E = Event of getting a total 10
= {(4, 6), (5, 5), (6,4)}
∴ n(E) = 3
∴ P(getting a total of 10) = P(E) = \(\frac{n(E)}{n(S)}=\frac{3}{36}=\frac{1}{12}\)
and P(not getting a total of 10) = P(Ē)
1 – P(E) = 1 – \(\frac{1}{12}\) = \(\frac{1}{11}\)
Thus, P(A getting 10) = \(\frac{1}{12}\) and P(B getting 10) and P(A is not getting 10) = P(B is not getting 10) = \(\frac{11}{12}\)
Now, P(A winning) = = P(Ā ∩ B) + P (Ā ∩ B̄ ∩ Ā) + P(Ā ∩ B̄ ∩ Ā ∩ B̄ ∩ Ā) + …
= P(Ā) + P(Ā)P(B̄)P(A) + P(Ā)P(B̄)P(Ā)P(B̄)P(A) + ……..

Question 8.
Probabilities of solving a specific problem independently by A and B are \(\frac{1}{2}\) and \(\frac{1}{3}\), respectively. If both try to solve problem independently, then find the probability that
(i) problem is solved.
(ii) exactly one of them solves the problem. (All India 2015C, Delhi 2011)
Answer:
The problem is solved means atleast one of them solve it. Also, use the concept A and B are independent events, then their complements are also independent.
Let P(A) = Probability that A solves the problem
P(B) = Probability that B solves the problem
P(Ā) = Probability that A does not solve the problem
and P(Ā) = Probability that B does not solve the problem.
According to the question, we have

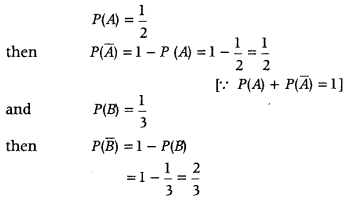
(i) P (problem is solved)
= P (A ∩ B̄) + P(Ā ∩ B) + P (A ∩ B)
= P(A) ∙ P(B̄) + P(Ā) ∙ P(B) + P(A) ∙ P(B)
[∵ A and B are independent events]
= \(\left(\frac{1}{2} \times \frac{2}{3}\right)+\left(\frac{1}{2} \times \frac{1}{3}\right)+\left(\frac{1}{2} \times \frac{1}{3}\right)\)
= \(\frac{2}{6}+\frac{1}{6}+\frac{1}{6}=\frac{4}{6}=\frac{2}{3}\)
Hence, probability that the problem is solved, is \(\frac{2}{3}\).

(ii) P (exactly one of them solve the problem)
= P (A solve but B do not solve) + P (A do not solve but B solve)
= P(A ∩ B̄) + P(Ā ∩ B)
= P(A) ∙ P(B̄) + P(Ā) ∙ P(B)
= \(\left(\frac{1}{2} \times \frac{2}{3}\right)\) = \(\left(\frac{1}{2} \times \frac{1}{3}\right)\) = \(\frac{2}{6}+\frac{1}{6}=\frac{3}{6}=\frac{1}{2}\)

Alternate Method
P (problem is solved)
= 1 – P (none of them solve the problem)
= 1 – P(Ā ∩ B̄)
= l – P(Ā) ∙ P(B̄) = 1 – \(\left(\frac{1}{2} \times \frac{2}{3}\right)\)
∵ P(Ā) = \(\frac{1}{2}\) and P(B̄) = \(\frac{2}{3}\)
= 1 – \(\frac{1}{3}\) = \(\frac{2}{3}\)

(ii) P (exactly one of them solve the problem)
= P(A) + P(B) – 2P(A ∩ B)
= P(A) + P(B) – 2P(A) × P(A)
= \(\frac{1}{2}+\frac{1}{3}-2 \times \frac{1}{2} \times \frac{1}{3}=\frac{1}{2}\)

Question 9.
A couple has 2 children. Find the probability that both are boys, if it is known that
(i) one of them is a boy.
(ii) the older child is a boy. (Delhi 2014C, All India 2014, 2010)
Answer:
Firstly, write the sample space of given data. Then, use concept of conditional probability
P(A / B) = \(\frac{P(A \cap B)}{P(B)}\) to get the desired result.

Let B and b represent older and younger boy child. Also, let G and g represent older and younger girl child. The sample space of the given question is S = {Bb, Bg, Gg, Gb}
∴ n(S) = 4
Let A be the event that both children are boys.
Then, A = {Bb}
∴ n(A) = 1

(i) Let B : Atleast one of the children is a boy
∴ B = {Bb, Bg, Gb} and n(B) = 3

(ii) Let C : The older child is a boy.
Then, C = {Bb, Bg}
∴ n(C) = 2

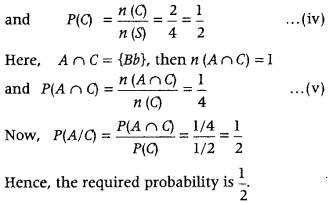
Question 10.
Assume that each born child is equally likely to be a boy or a girl. If a family has two children, then what is the conditional probability that both are girls? Given that
(i) the youngest is a girl?
(ii) atleast one is a girl? (Delhi 2014)
Answer:
Let B and b represent elder and younger boy child. Also, G and g represent elder and younger girl child. If a family has two children, then all possible cases are
S = {Bb, Bg, Gg, Gb}
∴ n(S) = 4
Let us define event A : Both children are girls, then A = {Gg} ⇒ n(A) = 1
(i) Let E ₁ : The event that youngest child is a girl.
Then, E ₁ = {Bg, Gg} and n(E ₁ ) = 2

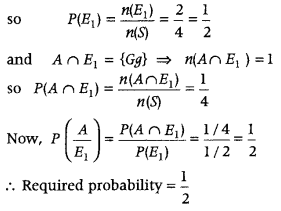
(ii) Let E ₂ : The event that atleast one is girl.
Then, E ₂ = {Eg, Gg, Gb} ⇒ n(E ₂ ) = 3,

Question 11.
A speaks truth in 75% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact? Do you think that statement of B is true? (All India 2013)
Answer:
Let A _T : Event that A speaks truth
and B _T : Event that B speaks truth.
Given, P(A _T ) = \(\frac{75}{100}\), then P(Ā _T ) = 1 – \(\frac{75}{100}\)
[∵ P(Ā) = 1 – P(A)]
= \(\frac{25}{100}\)
and P(B _T ) = \(\frac{90}{100}\)
Then, P(B̄ _T ) = 1 – \(\frac{90}{100}\) = \(\frac{10}{100}\)
Now, P (A and B are contradict to each other)

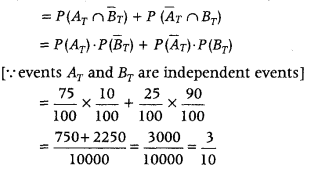
∴ Percentage of P (A and B are contradict to each other) = \(\frac{3}{10}\) × 100 = 30%
Since, B speaks truth in only 90% (i.e. not 100%) of the cases, therefore we think, the statement of B may be false.

Question 12.
P speaks truth in 70% of the cases and Q in 80% of the cases. In what percent of cases are they likely to agree in stating the same fact? Do you think, when they agree, means both are speaking truth? (All India 2013)
Answer:
Let p _T : Event that P speaks truth
and Q _T : Event that Q speaks truth.

No, agree does not mean that they are speaking truth.

Question 13.
A speaks truth in 60% of the cases, while B in 90% of the cases. In what percent of cases are they likely to contradict each other in stating the same fact? In the cases of contradiction do you think, the statement of B will carry more weight as he speaks truth in more number of cases than A? (Delhi 2013)
Answer:
42% Yes

Question 14.
If A and B are two independent events such that P(Ā ∩ B) = \(\frac{2}{15}\) and (A ∩ B̄) = \(\frac{1}{6}\), then find P (A) and P (B). (Delhi 2015)
Answer:
Given, A and B are two independent events with
P(Ā ∩ B) = \(\frac{2}{15}\) and P(A ∩ B) = \(\frac{1}{6}\).
We know that, if A and B are independent, then Ā, B and A, B̄ are independent events.

Question 15.
Consider the experiment of tossing a coin. If the coin shows head, toss it again, but if it shows tail, then throw a die. Find the conditional probability of the event that ‘the die shows a number greater than 4’, given that ‘there is atleast one tail’. (Delhi 2014C)
Answer:
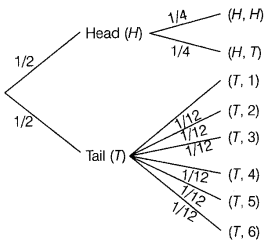
The sample space S of the experiment is given as
S = {(H, H), (H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
The probabilities of these elementary events are

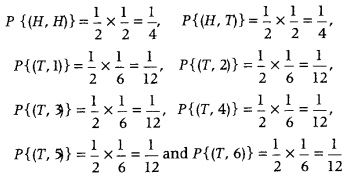
The outcomes of the experiment can be represented in the following tree diagram.

Consider the following events:
A = the die shows a number greater than 4 and
B = there is atleast one tail.
We have, A = {(T, 5), (T, 6)},
B = {(H, T), (T, 1), (T, 2), (T, 3), (T, 4), (T, 5), (T, 6)}
and A ∩ B = {(T, 5), (T, 6)}
∴ P(B) = P((H, T)) + P((T, 1)) + P((T, 2)) + P((T, 3)) + P((T, 4)) + P((T, 5)) + P((T, 6))
⇒ P(B) = \(\frac{1}{4}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{3}{4}\)
and P(A ∩ B) = P((T, 5)) + P((T, 6)) = \(\frac{1}{12}+\frac{1}{12}=\frac{1}{6}\)
∴ Required probability
= \(P\left(\frac{A}{B}\right)=\frac{P(A \cap B)}{P(B)}=\frac{1 / 6}{3 / 4}=\frac{4}{18}=\frac{2}{9}\)

Topic 2: Baye’s Theorem and Probability Distributions

Question 1.
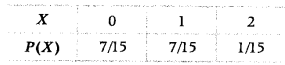
Find the probability distribution of X, the number of heads in a simultaneous toss of two coins. (All India 2019)
Answer:
When two coins are tossed, there may be 1 head, 2 heads or no head at all. Thus, the possible values of X are 0, 1, 2.
Now, P(X = 0) = P (Getting no head) = P(TT) = \(\frac{1}{4}\)
P(X = 1) = P (Getting one head) = P(HT or TH) = \(\frac{2}{4}=\frac{1}{2}\)
P(X = 2) = P (getting two heads) = P(HH) = \(\frac{1}{4}\)
Thus, the required probability distribution of X is

Question 2.
The random variable X has a probability distribution P(X) of the following form, where ‘k’ is some number.

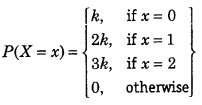
Determine the value of ‘k’. (Delhi 2019)
Answer:
Given,

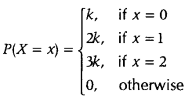
Making it in tabular format, we get the following

Since, sum of all probabilities is equal to 1. (112)
ΣP(X = x) = 1
⇒ P(X = 0) + P(X = 1) + P(X = 2) + 0 + 0 + ……. = 1
⇒ k + 2k + 3k = 1
⇒ 6k = 1 ⇒ k = \(\frac{1}{6}\)

Question 3.
Suppose a girl throws a the. If she gets 1 or 2, she tosses a coin three times and notes the number of tails. If she gets 3, 4, 5 or 6, she tosses a coin once and notes whether a ‘head’ or ‘tail’ is obtained. If she obtained exactly one ‘tail’, what is the probability that she threw 3, 4, 5 or 6 with the die? (C8SE 2019)
Answer:
Let E ₁ be the event that the girl gets 1 or 2.
E ₂ be the event that the girl gets 3, 4, 5 or 6
and A be the event that the girl gets exactly a ‘tail’.
Then, P(E ₁ ) = \(\frac{2}{6}=\frac{1}{3}\)
and P(E ₂ ) = \(\frac{4}{6}=\frac{2}{3}\)
\(P\left(\frac{A}{E_{1}}\right)\) = P (getting exactly one tail when a coin is tossed three times) = \(\frac{3}{8}\)
\(P\left(\frac{A}{E_{2}}\right)\) = P (getting exactly a tail when a coin is tossed once) = \(\frac{1}{2}\)
Now, required probability

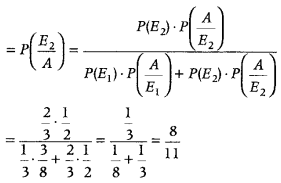
Question 4.
Two numbers are selected at random (without replacement) from the first five positive integers. Let X denotes the larger of the two numbers obtained. Find the mean and variance of X. (CBSE 2018)
Answer:
Total number of possible outcomes
= ⁵ P ₂ = \(\frac{5 !}{3 !}\) = 5 × 4 = 20
Here, X denotes the larger of two numbers obtained.
∴ X can take values 2, 3, 4 and 5.
Now, P(X = 2) = P (getting ( 1. 2) or (2, 1)) = \(\frac{2}{20}=\frac{1}{10}\)
P(X = 3) = P (getting (1, 3) or (3, 1) or (2, 3) or (3, 2) = \(\frac{4}{20}=\frac{2}{10}\)
P(X = 4) = P(getting(1,4) or (4, 1)or (2, 4) or (4, 2) or (3, 4) or (4, 3)) = \(\frac{6}{20}=\frac{3}{10}\)
and P(X = 5) = P (getting (1, 5) or (5, 1) or (2, 5) or (5, 2) or (3, 5) or (5, 3) or (4, 5) or (5, 4))
= \(\frac{8}{20}=\frac{4}{10}\)
Thus, the probability distribution of X is

Now, mean of X is E(X) = Σ X ∙ P(X)

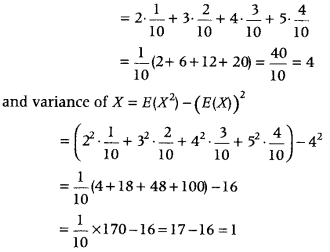
Question 5.
Two groups are competing for the positions of the Board of Directors of a corporation. The probabilities that the first and second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced way by the second group. (CBSE 2018C)
Answer:
Let E ₁ and E ₂ denote the events that first and second group will win. Then,
P(E ₁ ) = 0.6 and P(E ₂ ) = 0.4
Let E be the event of introducing the new product.
Then, P\(\left(\frac{E}{E_{1}}\right)\) = 0.7 and P\(\left(\frac{E}{E_{2}}\right)\) = 0.3
Now, we have to find the probability that new product is introduced by second event.

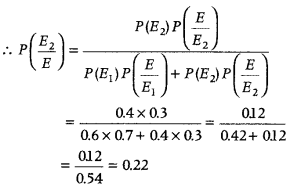
Question 6.
The random variable X can take only the values 0, 1, 2, 3. Given that
P(X = 0) = P(X = 1) = p and
P(X = 2) = P (X = 3) such that
Σp _i x _i ² = 2Σp _i x _i , find the value of P. (Delhi 2017)
Answer:
Given, X = 0, 1, 2, 3 and
P(X = 0) = P(X = 1) = p, P(X = 2) = P(X = 3)
such that Σp _i x _i ² = 2Σp _i x _i
Now, Σp _i = 1
⇒ p ₀ + p ₁ + p ₂ + p ₃ = 1
⇒ p + p + x + x = 1
[let P(X = 2) = P(X = 3) = x]
⇒ 2p + 2x = 1
⇒ 2x = 1 – 2p
⇒ x = \(\frac{1-2 p}{2}\)
The probability distribution of X is given by

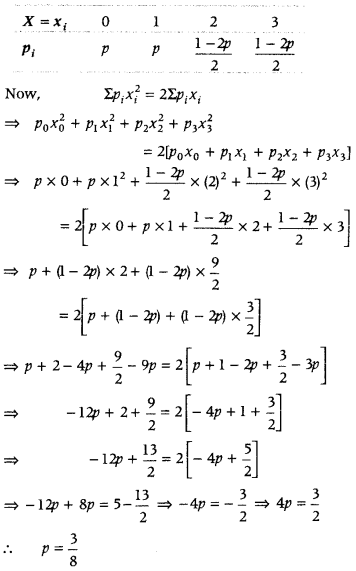
Question 7.
There are 4 cards numbered 1, 3, 5 and 7, one number on one card. Two cards are drawn at random without replacement. Let X denote the sum of the numbers on the two drawn cards. Find the mean and variance of X. (All India 2017)
Answer:
Here, S = {(1, 3), (1, 5), 1, 7), (3, 1), (3, 5), (3, 7), (5, 1), (5, 3), (5, 7), (7,1), (7, 3), (7, 5)}
⇒ n(S) = 12
Let random variable X denotes the sum of the numbers on two cards drawn. So, the random variables X may have values 4, 6, 8, 10 and 12.
At X = 4, P(X) = \(\frac{2}{12}=\frac{1}{6}\)
At X = 6, P(X) = \(\frac{2}{12}=\frac{1}{6}\)
At X = 8, P(X) = \(\frac{4}{12}=\frac{1}{3}\)
At X = 10, P(X) = \(\frac{2}{12}=\frac{1}{6}\)
At X = 12, P(X) = \(\frac{2}{12}=\frac{1}{6}\)
Therefore, the required probability distribution is as follows

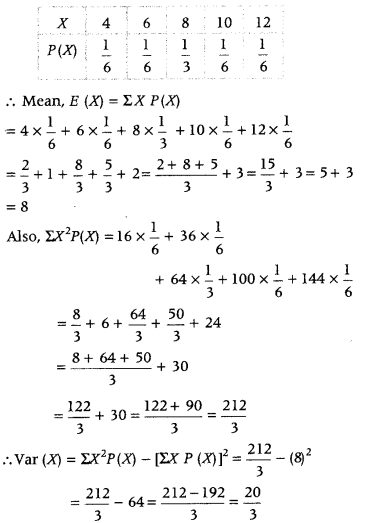
Question 8.
Three persons A, B and C apply for a job of Manager in a private company. Chances of their selection (A, B and C) are in the ratio 1:2:4. The probabilities that A, B and C can introduce changes to improve profits of the company are 0.8, 0.5 and 0.3, respectively. If the change does not take place, find the probability that it is due to the appointment of C. (Delhi 2016)
Answer:
Let us define the following events
A = selecting person A
B = selecting person B
C = selecting person C

Question 9.
A bag X contains 4 white balls and 2 black balls, while another bag Y contains 3 white balls and 3 black balls. Two balls are drawn (without replacement) at random from one of the bags and were found to be one white and one black. Find the probability that the balls were drawn from bag Y. (All India 2016)
Answer:
Let us define the following events:
E ₁ : Bag X is selected
E ₂ : Bag Y is selected
and E: Getting one white and one black ball in a draw of two balls.
Here, P(E ₁ ) = P(E ₂ ) = \(\frac{1}{2}\)
[∵ probability of selecting each bag is equal]
Now, \(P\left(\frac{E}{E_{1}}\right)\) = Probability of drawing one white and one black ball from bag X
= \(\frac{{ }^{4} C_{1} \times{ }^{2} C_{1}}{{ }^{6} C_{2}}=\frac{4 \times 2}{\frac{6 \times 5}{2 \times 1}}=\frac{16}{6 \times 5}=\frac{8}{15}\)
and \(P\left(\frac{E}{E_{2}}\right)\) = Probability of drawing one white and one black ball from bag Y
= \(\frac{{ }^{3} C_{1} \times{ }^{3} C_{1}}{{ }^{6} C_{2}}=\frac{3 \times 3}{\frac{6 \times 5}{2 \times 1}}=\frac{3}{5}\)
∴ The probability that the one white and one black balls are drawn from bag Y,

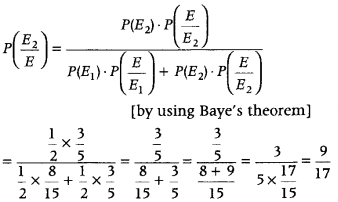
Question 10.
In a game, a man wins ₹ 5 for getting a number greater than 4 and loses ₹ 1 otherwise, when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a number greater than 4. Find the expected value of the amount he wins/loses. (All India 2016)
Answer:
Let X be a random variable that denotes the amount received by the man. Then, X can take values 5, 4, 3 and – 3.
Now, P(X = 5) = P (getting a number greater than 4 in the first throw) = \(\frac{2}{6}=\frac{1}{3}\)

P(X = 4) = P (getting a number less than or equal to 4 in the first throw and getting a number greater than 4 in the second throw) = \(\frac{4}{6} \times \frac{2}{6}=\frac{2}{9}\).

P(X = 3) = P (getting a number less than or equal to 4 in first two throws and getting a number greater than 4 in the third throw) = \(\frac{4}{6} \times \frac{4}{6} \times \frac{2}{6}=\frac{4}{27}\)

and P(X = – 3) = P (getting a number less than or equal to 4 in all three throws)
= \(\frac{4}{6} \times \frac{4}{6} \times \frac{4}{6}=\frac{8}{27}\)
Thus, the probability distribution of X is

Question 11.
A bag contains 4 balls. Two balls are drawn at random (without replacement) and are found to be white. What is the probability that all the balls in the bag are white? (All India 2016, 2014C)
Answer:
Let A : Two drawn balls are white
E ₁ : All the balls are white
E ₂ : Three balls are white
E ₃ : Two balls are white
Since, E ₁ , E ₂ and E ₃ are mutually exclusive and exhaustive events.
∴ P(E ₁ ) = P(E ₂ ) = P(E ₃ ) = \(\frac{1}{3}\)

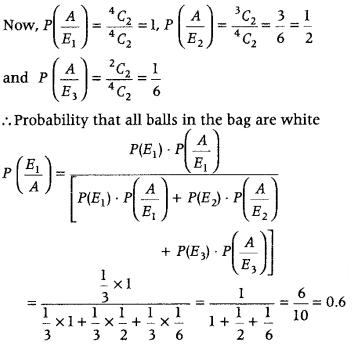
Question 12.
Let X denote the number of colleges where you will apply after your results and P(X = x) denotes your probability of getting admission in x number of colleges. It is given that

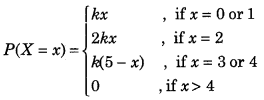
where k is a positive constant. Find the value of k. Also, find the probability that you will get admission in
(i) exactly one college
(ii) at most 2 colleges
(iii) at least 2 colleges. (Foreign 2016)
Answer:
We have,

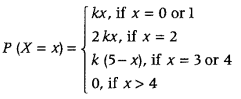
We know that, sum of ah the probabilities of a distribution is always 1.
∴ P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4) + …….. = 1
⇒ 0 + k + 4k + 2k + k + 0 + 0 + ………. = 1
⇒ 8k = 1 ⇒ k = \(\frac{1}{8}\)

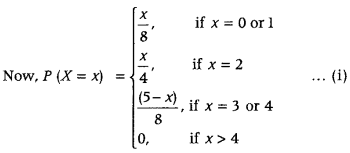
∴ (i) P (getting admission in exactly one college)
= P(X = 1) = \(\frac{1}{8}\) [using (i)]

(ii) P(getting admission in at most 2 colleges)
= P(X ≤ 2)
= P(X= 0) + P(X = 1) + P(X = 2)
= 0 + \(\frac{1}{8}+\frac{2}{4}=\frac{5}{8}\)

(iii) P (getting admission in at least 2 colleges)
= P(X ≥ 2) = 1 – P(X < 2)
= 1 – [P(X = 0) + P(X = 1))
= 1 – [0 + \(\frac{1}{8}\)] = 1 – \(\frac{1}{8}=\frac{7}{8}\)

Question 13.
A bag A contains 4 black and 6 red balls and bag B contains 7 black and 3 red balls. A die is thrown. If 1 or 2 appears on it, then bag A is chosen, otherwise bag B. If two balls are drawn at random (without replacement) from the selected bag, find the probability of one of them being red and another black. (Delhi 2015)
Answer:
Given, bag A = 4 black and 6 red balls
bag B = 7 black and 3 red balls.
Let E ₁ = The event that die show 1 or 2
E ₂ = The event that die show 3 or 4 or 5 or 6
E = The event that among two drawn balls, one of them is red and other is black

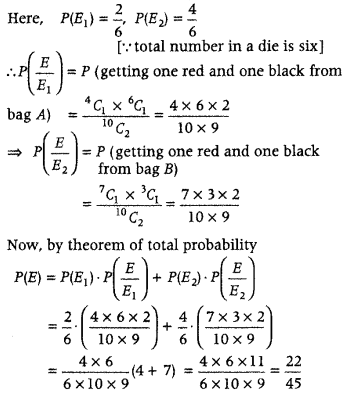
Question 14.
Three machines E ₁ , E ₂ and E ₃ in a certain factory producing electric bulbs, produce 50%, 25% and 25% respectively, of the total daily output of electric bulbs. It is known that 4% of the bulbs produced by each of machines E ₁ and E ₂ are defective and that 5% of those produced by machine E ₃ are defective. If one bulb is picked up at random from a day’s production, calculate the probability that it is defective. (Foreign 2015)
Answer:
Let A ₁ : Event that the bulb is produced by machine E ₁
A ₂ : Event that the bulb is produced by machine E ₂
A ₃ : Event Chat the bulb is produced by machine E ₃
A: Event that the picked up bulb is defective

Question 15.
Two numbers are selected at random (without replacement) from positive integers 2, 3, 4, 5, 6 and 7. Let X denote the larger of the two numbers obtained. Find the mean and variance of the probability distribution of X. (Foreign 2015)
Answer:
Given, X denotes larger of the two numbers be obtained.
Obviously X can values 3, 4, 5, 6 and 7.
Now,

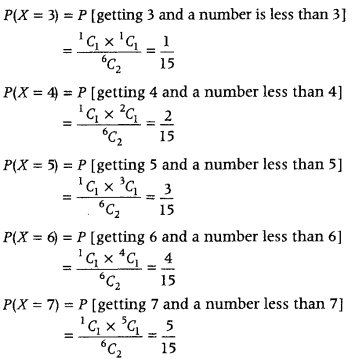
Therefore, required probability distribution is as follows

Question 16.
From a lot of 15 bulbs which include 5 defectives, a sample of 2 bulbs is drawn at random (without replacement). Find the probability distribution of the number of defective bulbs. (Delhi 2015C)
Answer:
It is given that out of 15 bulbs, 5 are defective.
∴ Number of non-defective bulbs = 15 – 5 = 10
Let X be the random variable which denotes the defective bulbs. So, X may take values 0, 1, 2
P(X = 0) = P (No defective bulb)
= \(\frac{10}{15} \times \frac{9}{14}=\frac{90}{210}=\frac{9}{21}\)
[∵ bulb is drawn without replacement]
P(X = 1) = P (One defective bulb and one non defective bulb)

Question 17.
Three cards are drawn at random (without replacement) from a well-shuffled pack of 52 playing cards. Find the probability distribution of number of red cards. Hence, find the mean of the distribution. (Foreign 2014)
Answer:
Let X be a random variable that denotes number of red cards in three draws.
Here, X can take values 0, 1, 2, 3.
Now, P(X = 0) = P (getting all black cards)
= \(\frac{{ }^{26} C_{3}}{{ }^{52} C_{3}}=\frac{26}{52} \times \frac{25}{51} \times \frac{24}{50}=\frac{2}{17}\)
P(X = 1) = P (getting one red card and two black cards)

Question 18.
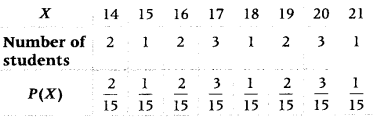
A class has 15 students whose ages are 14, 17, 15, 14, 21, 17, 19, 20, 16, 18, 20, 17, 16, 19 and 20 years. One student is selected in such a manner that each has the same chance of being chosen and the age X of the selected student is recorded. What is the probability distribution of the random variable XI Find the mean of X. (All India 2014C)
Answer:
Firstly, find the probability of respective ages and make a probability distribution tabLe then using the formula
Mean (X) = ΣX ∙ P(X), calculate mean.
Here, total students = 15
The ages of students in ascending order are
14, 14, 15, 16, 16, 17, 17, 17, 18, 19, 19, 20, 20, 20 and 21.
Now,
P(X = 14) = \(\frac{2}{15}\),
P(X = 15) = \(\frac{1}{15}\),
P(X = 16) = \(\frac{2}{15}\),
P(X = 17) = \(\frac{3}{15}\),
P(X = 18) = \(\frac{1}{15}\),
P(X = 19) = \(\frac{2}{15}\),
P(X = 20) = \(\frac{3}{15}\),
P(X = 21) = \(\frac{1}{15}\)
Therefore, the probability distribution of random variable X is as follows

∴ Mean(X) = ΣX ∙ P(X)

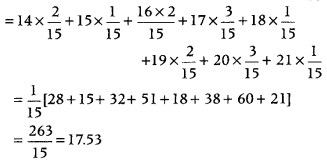
Question 19.
A bag contains 3 red and 7 black balls. Two balls are selected at random one by one without replacement. If the second selected ball happens to be red, what is the probability that the first selected ball is also red? (Delhi 2014C)
Answer:
Let E ₁ : First ball is red, E ₂ : First ball is black
A: Second ball is red (1)
Total number of balls is 10.
Then, P(E ₁ ) = \(\frac{3}{10}\), P(E ₂ ) = \(\frac{7}{10}\)
∴ \(P\left(\frac{A}{E_{1}}\right)=\frac{2}{9}\) and \(P\left(\frac{A}{E_{2}}\right)=\frac{3}{9}\)
Then, by Baye’s theorem, probability of second selected ball is red when first selected ball is also red is given by

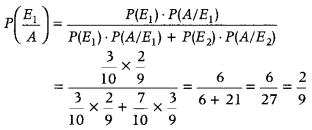
Hence, the probability that the first selected ball is red, is \(\frac{2}{9}\).

Question 20.
An urn contains 4 white and 6 red balls. Four balls are drawn at random (without replacement) from the urn. Find the probability distribution of the number of white balls. (Delhi 2012c)
Answer:
Let X be a random variable that denotes the number of white balls in a draw of 4 balls. Then, X can take values of 0, 1, 2, 3 and 4.
Clearly, P (X = 0) = P (getting no white ball)

Question 21.
Two cards are drawn simultaneously (without replacement) from a well-shuffled deck of 52 cards. Find the mean and variance of number of red cards. (All India 2012)
Answer:
Firstly, find the pobability distribution table of number of red cards. Then, using this table, find the mean and variance.
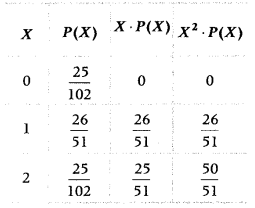
Let X be the number of red cards. Then, X can take values 0, 1 and 2.
Now, P(X = 0) = p (having no red card)

Now, we know that, mean = Σx ∙ P(x)
and variance = Σx ² ∙ P(x) – [Σx ∙ P(X)] ²

Question 22.
Find the mean number of heads in three tosses of a coin. (Foreign 2011)
Answer:
Firstly, we write the probability distribution table for the given experiment. Then, we find mean by using formula
Mean = ΣX _i P(x _i ).
Let X = Number of heads when a corn is tossed three times.
Sample space of given experiment is
S = {HHH, TTT, HHT, HTH, THH, TTH, THT, HTT}
X can take values 0, 1, 2 and 3.
Now, P(X = 0) = P (no head occur) = \(\frac{1}{8}\)
P(X = 1) = P (one head occur) = \(\frac{3}{8}\)
P(X = 2) = P (two heads occur) = \(\frac{3}{8}\)
P(X = 3) = P (three heads occur) = \(\frac{1}{8}\)
∴ The probability distribution is as follows

Now, for finding mean

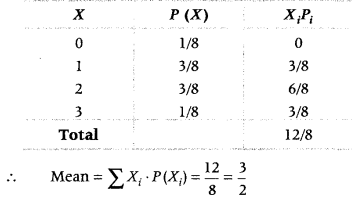
Question 23.
A random variable X has following probability distributions:

Find (i) k (ii) P(X < 3) (iii) P(X > 6) (iv) P (0 < X < 3). (All India 2011)
Answer:
Firstly, use the result that sum of all the probabilities of an experiment is one. Find k and then find other values by using this value of k.
(i) We know that, the sum of a probability distribution of random variable is one,
i.e. ΣP(X) = 1
0 + k + 2k + 2k + 3k + k ² + 2k ² + 7k ² + k = 1
10k ² + 9k – 1 = 0
10k ² + 10k – k – 1 = 0
10k(k + 1) – 1(k + 1) = 0
(10k -1) (k + 1) = 0
k = \(\frac{1}{10}\) or – 1
But k = – 1 is rejected because probability cannot be negative.
∴ k = \(\frac{1}{10}\)

(ii) P(X < 3) = P(X = 0) + P(X = 1) + P(X = 2)
= 0 + k + 2k = 3k
= \(3\left(\frac{1}{10}\right)\) [∵ k = \(\frac{1}{10}\)]
= \(\frac{3}{10}\)

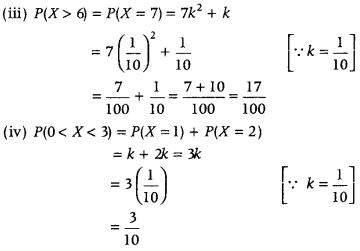
Question 24.
Find the probability distribution of number of doublets in three tosses of a pair of dice. (All India 2011C; Delhi 2010C)
Answer:
We know that, when a pair of dice is thrown, then total number of outcomes = 36
Also, probability of getting a doublet in one throw = \(\frac{6}{36}\) = \(\frac{1}{6}\)
[∵ doublets in pair of dice are (1, 1), (2, 2), (3, 3), (4, 4), (5, 5) and(6, 6)]
∴ Probability of not getting a doublet
= 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)
Let X = Number of doublets in three tosses of pair of dice
So, X can take values 0, 1, 2 and 3.
Now, P(X = 0) = P (not getting a doublet)
= \(\frac{5}{6} \times \frac{5}{6} \times \frac{5}{6}=\frac{125}{216}\)
P(X = 1) = P (getting a doublet once only)
= (getting a doublet in 1st throw) + P (getting a doublet in 2nd throw) + P (getting a doublet in 3rd throw)
= \(\left(\frac{1}{6} \times \frac{5}{6} \times \frac{5}{6}\right)+\left(\frac{5}{6} \times \frac{1}{6} \times \frac{5}{6}\right)+\left(\frac{5}{6} \times \frac{5}{6} \times \frac{1}{6}\right)\)
= \(\frac{25}{216}+\frac{25}{216}+\frac{25}{216}=\frac{75}{216}\)
P(X = 2) = P (getting a doublet two times)
= P (doublet in 1st and 2nd throw) + P (doublet in 2nd and 3rd throw) + P (doublet in 1st and 3rd throw)

Question 25.
Two cards are drawn successively with replacement from a well-shuffled deck of 52 cards. Find the probability distribution of number of aces. (Delhi 2011c)
Answer:
Let X = Number of aces
Since, two cards are drawn, so X can take values 0, 1 and 2.
Now, probability of getting an ace = \(\frac{4}{52}=\frac{1}{13}\) and probability of not getting an ace

Question 26.
Two cards are drawn simultaneously (without replacement) from a well-shuffled pack of 52 cards. Find the probability distribution of number of aces. Also, find the mean of distribution. (All India 2010C)
Answer:
Let X denotes the number of ace cards. Since, two cards are drawn, so X can take values 0, 1 and 2.
We know that, probability of getting an ace card

The probability distribution is as follows

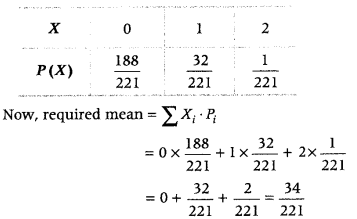
Question 27.
There are two bags, bag I and bag II. Bag I contains 4 white and 3 red balls while another bag II contains 3 white and 7 red balls. One ball is drawn at random from one of the bags and it is found to be white. Find the probability that it was drawn from bag I. (Delhi 2010)
Answer:
Let E ₁ be the event that Bag I is chosen,
E ₂ be the event that Bag II is chosen,
and A be the event that the drawn ball is white.
Then, P (E ₁ ) = \(\frac{1}{2}\)
P(E ₂ ) = \(\frac{1}{2}\)
p(A/E ₁ ) = \(\frac{4}{7}\),
and P(A/E ₂ ) = \(\frac{3}{10}\),
Now, (required probability = P(E ₁ /A)

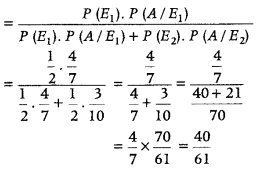
Question 28.
There are three coins. One is two-headed coin, another is biased coin that comes up heads 75% of the time and the third is an unbiased coin. One of three coins is chosen at random and tossed. If it shows heads, what is the probability that it is the two-headed coin? (All India 2019)
Answer:
Let E ₁ event of selecting two headed coin
E ₂ = event of selecting biased coin
E ₃ = event of selecting unbiased coin
A event of getting head
Then, P(E ₁ ) = P(E ₂ ) = P(E ₃ ) = \(\frac{1}{3}\)

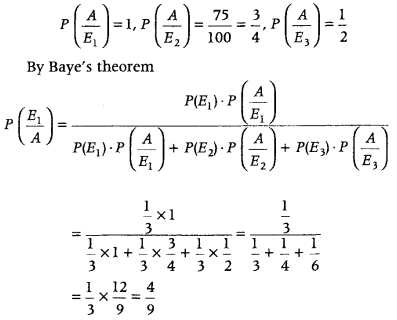
Question 29.
A bag contains 5 red and 4 black balls, a second bag contains 3 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random (without replacement) both of which are found to be red. Find the probability that the balls are drawn from the second bag. (All India 2019)
Answer:
Let E ₁ , E ₂ and A denote the following events
E ₁ = first bag is chosen, E ₂ = second bag is chosen and A = two balls drawn at random are red.
Since, one of the bag is chosen at random.
∴ P(E ₁ ) = P(E ₂ ) = \(\frac{1}{2}\)
If E ₁ has already occurred, i.e. first bag is chosen.
Therefore, the probability of drawing two red balls in this case

Question 30.
A manufacturer has three machine operators A, B and C. The first operator A produces 1% of defective items, whereas the other two operators B and C produces 5% and 7% defective items respectively. A is on the job for 50% of the time, B on the job 30% of the time and C on the job for 20% of the time. All the items are put into one stockpile and then one items is chosen at random from this and is found to be defective. What is the probability that it was produced by A? (Delhi 2019)
Answer:
Let A: Event that item produced by operator A
B: Event that item produced by operator B
C: Event that item produced by operator C
D: Event that item produced is defective
We need to find out the probability that item is produced by operator A if it is defective, i.e. P(A/D)
so,
P(A/D) = \(\frac{P(A) \cdot P(D / A)}{P(A) \cdot P(D / A)+P(B) \cdot P(D / B)+P(C) \cdot P(D / C)}\) ….. (i)
[by Baye’s theorem]
P(A) = Probability of item is produced by operator A
= 50% = \(\frac{50}{100}\) = 0.5
P(B) = Probability of item is produced by operator B
= 30% = \(\frac{30}{100}\) = 0.3
P(C) = Probability of item is produced by operator C
= 20% = \(\frac{20}{100}\) = 0.2
P(D/A) = Probability of a defective item produced by operator A
= 1% = \(\frac{1}{100}\) = 0.01
P(D/B) = Probability of a defective item produced by operator B
= 5% = \(\frac{5}{100}\) = 0.05
P(D / C) = Probability of a defective item produced by operator C
= 7% = \(\frac{7}{100}\) = 0.07
Putting these values in the Eq.(i), we get

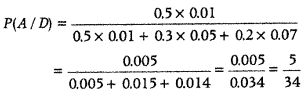
Therefore, required probability = \(\frac{5}{34}\).

Question 31.
Two cards are drawn simultaneously (or successively without replacement) from a well-shuffled pack of 52 cards. Find the mean and variance of the number of kings. (Delhi 2019)
Answer:
Let X be the number of kings obtained.
We can get 0, 1 or 2 kings.
So, value of X is 0, 1 or 2.
Total number of ways to draw 2 cards out of 52
i.e. Total ways = ⁵² C ₂ = 1326
P(X = 0)
i.e. Probability of getting 0 king
Number of ways to get 0 king
= Number of ways to select 2 cards out of non-king cards
= Number of ways to select 2 cards out of (52 – 4)
= 48 cards = ⁴⁸ C ₂ = 1128
P(X = 0) = \(\frac{\text { Number of ways to get } 0 \text { king }}{\text { Total number of ways }}\) = \(\frac{1128}{1326}\)
P(X = 1) i.e. Probability of getting 1 king
Number of ways to get 1 king
= Number of ways to select 1 king out of 4 king cards × Number of ways to select 1 card from 48 non-king cards
= ⁴ C ₁ × ⁴⁸ c ₁ = 4 × 48 = 192;
P(X = 1) = \(\frac{\text { Number of ways to get } 1 \text { king }}{\text { Total number of ways }}\) = \(\frac{192}{1326}\)
P(X = 2), i.e. Probability of getting 2 kings
Number of ways to get 2 king
= Number of ways of selecting 2 kings out of 4 king cards

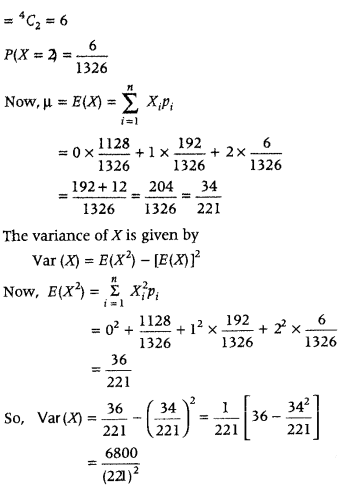
Question 32.
Three numbers are selected at random (without replacement) from first six positive integers. Let X denotes the largest of the three numbers obtained. Find the probability distribution of X. Also, find the mean and variance of the distribution. (All India 2016)
Answer:
We have, first six positive integers as 1, 2, 3, 4, 5 and 6 and let X denotes the largest of the three positive integers.
So, the random variable X may have values 3, 4, 5 or 6.
P(X = 3) = P [getting 3 and two numbers less than 3]
= \(\frac{{ }^{1} C_{1} \times{ }^{2} C_{2}}{{ }^{6} C_{3}}=\frac{1}{20}\)
P(X = 4) = P [getting 3 and two numbers less than 4]
= \(\frac{{ }^{1} C_{1} \times{ }^{3} C_{2}}{{ }^{6} C_{3}}=\frac{3}{20}\)
P(X = 5) = P [getting 3 and two numbers less than 5]
= \(\frac{{ }^{1} C_{1} \times{ }^{4} C_{2}}{{ }^{6} C_{3}}=\frac{6}{20}\)
P(X = 6) = P [getting 3 and two numbers less than 6]
= \(\frac{{ }^{1} C_{1} \times{ }^{5} C_{2}}{{ }^{6} C_{3}}=\frac{10}{20}\)
∴ The probability distribution is shown below

Question 33.
Bag A contains 3 red and 5 black balls, while bag B contains 4 red and 4 black balls. Two balls are transferred at random from bag A to bag B and then a ball is drawn from bag B at random. If the ball drawn from bag B is found to be red, find the probability that two red balls were transferred from A to B. (Foreign 2016)
Answer:

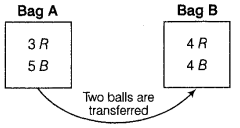
Let us define the following events:
E ₁ = one red and one black ball is transferred
E ₂ = two red balls are transferred
E ₃ = two black balls arc transferred
E = drawn ball is red.
Then,

Question 34.
In a factory which manufactures bolts, machines A, B and C manufacture respectively 30%, 50% and 20% of the bolts. Of their outputs, 3%, 4% and 1% respectively are defective bolts. A bolt is drawn at random from the product and is found to be defective. Find the probability that this is not manufactured by machine B. (All India 2015)
Answer:
Let E ₁ : Event that the selected bolt is manufactured by machine A.
E ₂ : Event that the selected bolt is manufactured by machine B,
E ₃ : Event that the selected bolt is manufactured by machine C,
and E : Event that the selected bolt is defective.

Question 35.
In answering a question on a multiple choice test, a student either knows the answer or guesses. Let \(\frac{3}{5}\) be the probability that he knows the answer and \(\frac{2}{5}\) be the probability that he guesses.
Assuming that a student who guesses at the answer will be correct with probability \(\frac{1}{3}\), what is the probability that the student knows the answer given that he answered it correctly? (All India 2015C)
Answer:
Let E ₁ : Event that the student knows the answer
E ₂ : Event that the student guesses the answer
E: Event that the answer is correct
Here, E ₁ and E ₂ are mutually exclusive and exhaustive events.
∴ P(E ₁ ) = \(\frac{3}{5}\) and P(E ₂ ) = \(\frac{2}{5}\)
Now, \(P\left(\frac{E}{E_{1}}\right)\) = P (the student answered correctly, given he knows the answer) = 1
\(P\left(\frac{E}{E_{2}}\right)\) = P (the student answered correctly, given he guesses) = \(\frac{1}{3}\)
The probability that the student knows the answer given that he answered it correctly is given by \(P\left(\frac{E_{1}}{E}\right)\).
By using Baye’s theorem, we get

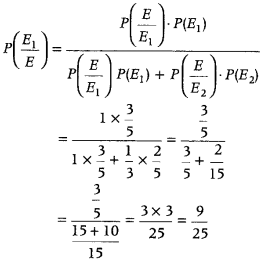
Question 36.
A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random without replacement from the bag and are found to be both red. Find the probability that the balls are drawn from the first bag. (Delhi 2015C)
Answer:
\(\frac{6}{7}\)

Question 37.
Two numbers are selected at random (without replacement) from the first six positive integers. Let X denotes the larger of the two numbers obtained. Find the probability distribution of the random variable X and hence, find the mean of the distribution. (All India 2014)
Answer:

and mean = \(\frac{14}{3}\)

Question 38.
There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up heads 75% of the times and third is also a biased coin that comes up tails 40% of the times. One of the three coins is chosen at random and tossed and it shows head. What is the probability that it was the two headed coin? (All India 2014)
Answer:
\(\frac{20}{47}\)

Question 39.
In a game, a man wins rupees five for a six and loses rupee one for any other number, when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins/loses. (All India 2014C)
Answer:
0

Question 40.
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probabilities of an accident for them are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver or a car driver? (Foreign 2014; All India 2009C)
Answer:
Let us define the events as
E ₁ : Insured person is a scooter driver
E ₂ : Insured person is a car driver
E ₃ : Insured person is a truck driver
A : Insured person meets with an accident
Then, n(E ₁ ) = 2000, n(E ₂ ) = 4000 and n(E ₃ ) = 6000
Here, total insured person, n(S) =12000
Now, P(E ₁ ) = Probability that the insured person is a scooter driver = \(\frac{n\left(E_{1}\right)}{n(S)}=\frac{2000}{12000}=\frac{1}{6}\)
n(S) 12000 6 (1)
P(E ₂ ) = Probability that the insured person is a car driver = \(\frac{n\left(E_{2}\right)}{n(S)}=\frac{4000}{12000}=\frac{1}{3}\)
and P(E ₃ ) = Probability that the insured person is a truck driver = \(\frac{n\left(E_{3}\right)}{n(S)}=\frac{6000}{12000}=\frac{1}{2}\)
Also, P(A/E ₁ ) = Probability that scooter driver meets with an accident 0.01
P(A/E ₂ ) = Probability that car driver meets with an accident = 0.03
and P(A/E ₃ ) = Probability that truck driver meets with an accident = 0.15
The probability that the person met with an accident was a scooter driver,

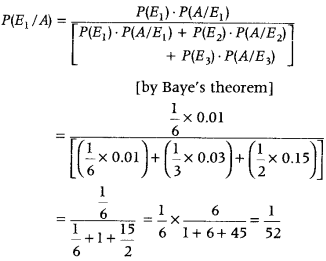
The probability that the person met with an accident was a car driver, P(E ₂ / A)

Question 41.
A man is known to speak the truth 3 out of 5 times. He throws a die and reports that it is ‘1’. Find the probability that it is actually 1. (Delhi 2014C)
Answer:
Let E ₁ = Event that 1 occurs in a die
E ₂ = Event that 1 does not occur in a die
A = Event that the man reports that 1 occur in a die
Then, P(E ₁ ) = \(\frac{1}{6}\) and P(E ₂ ) = \(\frac{5}{6}\)
∴ P (man reports that I occurs when 1 occur) = \(P\left(\frac{A}{E_{1}}\right)=\frac{3}{5}\)
and P (man reports that 1 occur but 1 does not occur)
= \(P\left(\frac{A}{E_{2}}\right)=\frac{2}{5}\)
Thus, by Baye’s theorem, we get
P(get actually 1 when he reports that 1 occur)

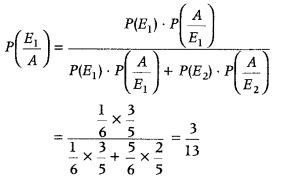
Question 42.
A card from a pack of 52 playing cards is lost. From the remaining cards of the pack three cards are drawn at random (without replacement) and are found to be all spades. Find the probability of the lost card being a spade. (Delhi 2014)
Answer:
Let us define the following events:
E ₁ = lost card is a spade card
E ₂ = lost card is not a spade card
A = drawn cards are spade cards
Then,

Question 43.
Assume that the chances of a patient having a heart attack is 40%. Assuming that a meditation and yoga course reduces the risk of heart attack by 30% and prescription of certain drug reduces its chance by 25%. At a time, a patient can choose anyone of the two options with equal probabilities. It is given that after going through one of the two options, the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga. Interpret the result and state which of the above stated methods, is more beneficial for the patient? (Delhi 2013)
Answer:
Let E ₁ : The patient follows meditation and yoga.
E ₂ : The patient uses drug.
Then, E ₁ and E ₂ are mutually exclusive
and P(E ₁ ) = P(E ₂ ) = 1/2
Also, let E : The selected patient suffers a heart attack.

yoga course and meditation are more beneficial for the heart patient.

Question 44.
An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers, the probability of their meeting an accident respectively are 0.01, 0.03 and 0.15. One of the insured persons meets with an accident. What is the probability that he is a car driver? (All India 2012C)
Answer:
\(\frac{3}{26}\)

Question 45.
Bag I contains 3 red and 4 black balls and bag II contains 4 red and 5 black balls. Two balls are transferred at random from bag I to bag II and then a ball is drawn from bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred balls were both black. (Delhi 2012)
Answer:
\(\frac{4}{17}\)

Question 46.
Among the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of all students who reside in hostel attain A grade and 20% of day scholars attain A grade in their annual exams. At the end of year, one student is chosen at random from the college and he has A grade, what is the probability that the student is a hosteler? (Delhi 2012,2011C)
Answer:
Let us define the events as
E ₁ : Students reside in a hostel
E ₂ : students are day scholars
A : Students get A grade
Then.
P(E ₁ ) = Probability that student reside in a hostel
= 60% = \(\frac{60}{100}\)
and P(E ₂ ) = Probability that students are day scholars = 1 – \(\frac{60}{100}=\frac{40}{100}\)
Also, P(A/E ₁ ) = Probability that hostelers get A grade = 30% = \(\frac{30}{100}\)
and P(A/E ₂ ) = Probability that students having day scholars get A grade = 20% = \(\frac{20}{100}\)
∴ The probability that the selecting student is a hosteler having A grade,

Question 47.
Suppose a girl throws a die. If she gets 5 or 6, then she tosses a coin 3 times and note the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin once and note whether a head or tail is obtained. If she obtained exactly one head, then what is the probability that she throw 1, 2, 3 or 4 with the die? (All India 2012)
Answer:
Let us define the events as
E ₁ : Girl gets 5 or 6 on a die
E ₂ : Girl gets 1, 2, 3 or 4 on a die
A: She gets exactly one head
Now, P(E ₁ ) = Probability of getting 5 or 6 on a die = \(\)
and P(E ₂ ) = Probability of getting 1, 2, 3 or 4 on a die = \(\)
Also, P(A/E ₁ ) = Probability that girl gets exactly one head when she throws coin thrice = \(\)
[∵ {HHH, TTT, HHT, HTH, THH, TTH, THT, TTH)]
P(A/E ₂ ) = Probability that girl gets exactly one head when she throws coin once
= \(\frac{1}{2}\)
The probability that she throws 1, 2, 3 or 4 with the die for getting exactly one head,

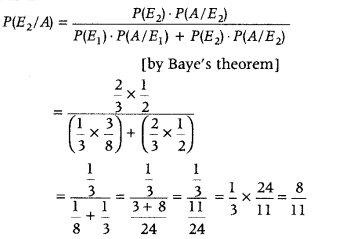
Question 48.
A girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin two times and notes the number of heads obtained. If she obtained exactly two heads, what is the probability that she threw 1,2,3 or 4 with the die? (Delhi 2012)
Answer:
\(\frac{4}{7}\)

Question 49.
Suppose 5% of men and 0.25% of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females. (Delhi 2011)
Answer:
Let us define the events as
E ₁ : Person selected is a male
E ₂ : Person selected is a female
A: Person selected has grey hair
Now, P(E ₁ ) = P (person selected is a male) = 1/2
and P(E ₂ ) = P (person selected is a female) = \(\frac{1}{2}\)
[∵ there are equal number of males and females] Now, P(A/E ₁ ) = Probability of selecting a person having grey hair is male = \(\frac{5}{100}\)
and P(A/E ₂ ) = Probability of selecting a person having grey hair is female = \(\frac{0.25}{100}\)
The probability of selecting person is a male having grey hair,

Question 50.
Bag I contains 3 red and 4 black balls and bag II contains 5 red and 6 black balls. One ball is drawn at random from one of the bags and is found to be red. Find the probability that it was drawn from bag II. (Delhi 2011)
Answer:
\(\frac{35}{68}\)

Question 51.
A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six. (Delhi 2011)
Answer:
\(\frac{3}{8}\)

Question 52.
A factory has two machines A and B. Past record shows that machine A produced 60% of items of output and machine B produced 40% of items. Further, 2% of items, produced by machine A and 1% produced by machine B were defective. All the items are put into a stockpile and then one item is chosen at random from this and this is found to be defective. What is the probability that it was produced by machine B ? (Foreign 2011)
Answer:
\(\frac{1}{4}\)

Question 53.
There are three identical boxes I, II and III, each containing two coins. In box I, both coins are gold coins, in box II, both are silver coins and in box III, there is one gold and one silver coin. A person chooses a box at random and take out a coin. If the coin is of gold, then what is the probability that the other coin in box is also of gold? (All India 2011)
Answer:
Let us define the events as
E ₁ : Box I is selected
E ₂ : Box Ills selected
E ₃ : Box III is selected
A: The drawn coin is a gold coin
Since events E ₁ , E ₂ and E ₃ are mutually exclusive and exhaustive events.
∴ P(E ₁ ) = P(E ₂ ) = P(E ₃ ) = \(\frac{1}{3}\)
Now, P(A/E ₁ )
= Probability that a gold coin is drawn from box I = \(\frac{2}{2}\) = 1 [∵ box II contain both gold coins] P(A/E ₃ ) = Probability that a gold coin is drawn from box II = 0 [∵ box II has both silver coins I and P(A / E ₃ ) = Probability that a gold coin is drawn from box III = \(\frac{1}{2}\)

[∵ box III contains I gold and 1 silver coin] The probability that other coin in box is also of gold = The probability that the drawing gold corn from bag I,

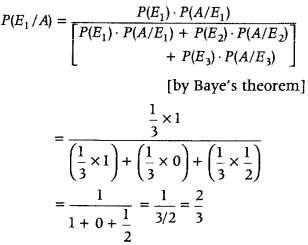
Hence, the required probability is \(\frac{2}{3}\)

Question 54.
There are three coins. One is a two tailed coin (having tail on both faces), another is a biased coin that comes up heads 60% of the times and third is an unbiased coin. One of the three coins is chosen at random and tossed and it shows tail. What is the probability that it is a two tailed coin? (All India 2011C)
Answer:
\(\frac{10}{19}\)

Question 55.
In a class, 5% of boys and 10% of girls have an IQ of more than 150. In the class, 60% are boys and rest are girls. If a student is selected at random and found to have an IQ of more than 150, then find the probability that the student is a boy. (All India 2010C)
Answer:
Let us define the events as
E ₁ : Boy is selected
E ₂ : Girl is selected
A: The student has an ¡Q of more than 150 students.
Now, P(E ₁ ) = 60% = \(\frac{60}{100}\)
Now, P(E ₂ ) = 40% = \(\frac{40}{100}\)
[∵ in the class 60% students are boys, so 40% arc girls, given ]
Now, P(A/E ₁ ) = Probability that boys has an IQ of more than 150 = 5% = \(\frac{5}{100}\)
and P(A/E ₂ ) = Probability that girls has an IQ of more than 150 = 10% = \(\frac{10}{100}\)
The probability that the selected boy having IQ more than 150 is

Hence, the required probability is 3/7.

Question 56.
In a bolt factory, machines A, B and C manufacture 25%, 35% and 40% of total production, respectively. Out of their total output, 5%, 4% and 2% are defective bolts. A bolt is drawn at random and is found to be defective. What is the probability that it is manufactured by machine B ? (Delhi 2010C)
Answer:
\(\frac{28}{69}\)

Question 57.
A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn at random and are found to both of clubs. Find the probability of the lost card being of clubs. (Delhi 2010)
Answer:
\(\frac{11}{50}\)

Question 58.
From a lot of 10 bulbs, which includes 3 defectives, a sample of 2 bulbs is drawn at random. Find the probability distribution of number of defective bulbs? (Delhi 2010)
Answer: