Students must start practicing the questions from CBSE Sample Papers for Class 12 Physics with Solutions Set 9 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Physics Set 9 with Solutions
Time : 3 hrs
Max. Marks : 70
Instructions
1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary.
(i) c = 3 × 10
8
m/s
(ii) m
e
= 9.1 × 10
-31
kg
(iii) e = 1.6 × 10
-19
C
(iv) µ
0
= 4π × 10
-7
TmA× 10
-1
(v) h = 6.63 × 10
-34
Js
(vi) ε
0
= 8.854 × 10
-112
C
2
N
-1
m
-2
(vii) Avogadro’s number = 6.023 × 10
23
per gram mole
Section A
Question 1.
A surface S = 10 \(\hat{\mathbf{j}}\) is kept in an electric field E = \(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}+7 \hat{\mathbf{k}}\). How much electric flux will come out through this surface?
(a) 40 unit
(b) 50 unit
(c) 30 unit
(d) 20 unit
Answer:
(a) 40 unit
Electric flux through the. surface, ϕ = E • S
= \(2 \hat{\mathbf{i}}+4 \hat{\mathbf{j}}+7 \hat{\mathbf{k}}\) ⋅ 10 \(\hat{\mathbf{j}}\)
= 40 unit
Question 2.
The work done to move a charge along an equipotential from A to B,
(a) cannot be defined as –\(\int_A^B \mathbf{E} \cdot d \mathbf{l}\)
(b) must be defined as \(\int_A^B \mathbf{E} \cdot d \mathbf{l}\)
(c) is zero
(d) can have a non-zero value
Answer:
(c) is zero
Work done in displacing a charge particle is
given by W
12
= q(V
2
– V
1
)
and the line integral of electrical field from point 1 to point 2 gives potential differenceV
2
– V
1
= \(\int_1^2 \mathbf{E} \cdot d \mathbf{l}\)
For equipotential surface, V
2
– V
1
= 0
W = 0
Question 3.
The momentum of the photon of wavelength 5000 A will be [1]
(a) 1.3 × 10
-27
kg-ms
-1
(b) 1.3 × 10
-28
kg-ms
-1
(c) 4 × 10
-29
kg-ms
-1
(d) 4 × 10
-18
kg-ms
-1
Answer:
(a) 1.3 × 10
-27
kg-ms
-1
Momentum, p = \(\frac{ h }{ λ }\)
= \(\frac{6.6 \times 10^{-34}}{\left(5000 \times 10^{-10}\right)}\)
= 1.3 × 10
-27
kg-ms
-1
Question 4.
The ground state energy of hydrogen atom is – 13.6 eV. What is the potential energy of the electron in this state? [1]
(a) 0 eV
(b) -27.2 eV
(c) 1 eV
(d) 2 eV
Answer:
(b) -27.2 eV
Potential energy of electron in ground state
= 2 × Total energy in this state
= 2 × (- 13.6 eV) = – 27.2 eV
Question 5.
In the figure shown, there are two semi-circles of radii rx and r2 in which a current i is flowing. The magnetic induction at the centre O will be [1]
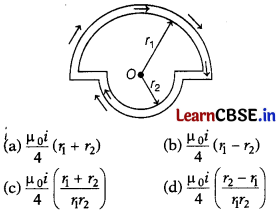
Answer:
(c) \(\frac{\mu_0 i}{4}\) (\(\frac{r_1+r_2}{r_1 r_2}\))
The direction of magnetic field produced due to both semi-circulars parts will be perpendicular to the paper and inwards.
Also, B = B
1
+ B
2
= \(\frac{\mu_0 i}{4 r_1}\) + \(\frac{\mu_0 i}{4 r_2}\)
= \(\frac{\mu_0 i}{4}\) (\(\frac{r_1+r_2}{r_1 r_2}\))
Question 6.
A bar magnet of magnetic moment M is placed in a magnetic field of induction B. The torque exerted on it is [1]
(a) M × B
(b) -B ⋅ M
(c) M ⋅ B
(d) M + B
Answer:
(a) M × B
Torque, τ = MB sin .
where, Mis magnetic moment, B is magnetic field and θ is angle between them.
∴ τ = M × B
Question 7.
If a charged spherical conductor of radius 10 cm has potential V at a point distant 5 cm from its centre, then the potential at a point distant 15 cm from the centre will be [1]
(a) \(\frac{1}{3}\)v
(b) \(\frac{2}{3}\)y
(c) \(\frac{3}{2}\)y
(d) 3V
Answer:
(b) \(\frac{2}{3}\)y
Potential at a point distance R is given by
V = \(\frac{K Q}{R}\)
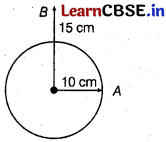
Potential at point A (R = 10cm),
V
A
= \(\frac{K Q}{10}\) …..(i)
Similarly, potential at point B (R – 15cm)
V
B
= \(\frac{K Q}{15}\) …..(ii)
Dividing Eq. (ii) by Eq. (i), we get
\(\frac{V_B}{V_A}\) = \(\frac{K Q}{15}\) × \(\frac{10}{K Q}\) = \(\frac{10}{15}\) = \(\frac{2}{3}\)
or V
B
= \(\frac{2}{3}\) V
A
= \(\frac{2}{3}\) V
Since, potential inside the spherical conductor is equal to the potential on the surface.
V
A
= V
(V is potential, R = 5cm, i.e. inside)
∴ V
B
= 4V
Question 8.
Which of the following relation is correct? [1]
(a) \(\sqrt{\varepsilon_0 E_0}=\sqrt{\mu_0 B_0}\)
(b) \(\sqrt{\mu_0 \varepsilon_0}=\frac{B_0}{E_0}\)
(c) \(E_0=\sqrt{\mu_0 \varepsilon_0 B_0}\)
(d) \(\sqrt{\mu_0 E_0}=\sqrt{\varepsilon_0 B_0}\)
Answer:
(b) \(\sqrt{\mu_0 \varepsilon_0}=\frac{B_0}{E_0}\)
As, \(\frac{E_0}{B_0}\) = c = \(\sqrt{\mu_0 \varepsilon_0}\)
⇒ \(\sqrt{\mu_0 \varepsilon_0}\) = \(\frac{B_0}{E_0}\)
Question 9.
The transformation ratio in the step-up transformer is [1]
(a) 1
(b) greater than one
(b) less than one
(d) the ratio greater or less than one depends on the other factor.
Answer:
(b) greater than one
Transformation ratio,
k = \(\frac{N_S}{N_P}\) = \(\frac{V_S}{V_P}\)
For step-up transformer V
S
> V
P
N
S
> N
P
Hence, K > 1
Question 10.
In a circuit with a coil of resistance 2 Ω, the magnetic flux charges from 2.0 Wb to 10.0 Wb in 0.2s. The charge that flows in the coil during this time is [1]
(a) 5.0 C
(b) 4.0 C
(d) 1.0 C
(d) 0.8 C
Answer:
(b) 4.0 C
∆Q = \(\frac{\Delta \phi}{R}\) = \(\frac{(10-2)}{2}\) = 4C
Question 11.
The magnetic flux across a loop of resistance 10 Q is given by ϕ = (5t² – 4t +1) Wb. How much current is induced in the loop after 0.2 s? [1]
(a) 0.4 A
(b) 0.2 A
(c) 0.04 A
(d) 0.02 A
Answer:
(b) 0.2 A
Given that, ϕ = (5t² – 4t + 1) Wb
\(\frac{d \phi}{d t}\) = (10t – 4) Wbs
-1
Induced emf, e = –\(\frac{d \phi}{d t}\) = -(10 t – 4)
At t = 0.2 s, e = – (10 × 0.2 – 4) = 2 V
Induced current, I = \(\frac{e}{R}\) = \(\frac{2 \mathrm{~V}}{10 \Omega}\) = 0.2 A
Question 12.
In hydrogen atom, if the difference in the energy of the electron in n = 2 and n =3 orbits is E, the ionisation energy of hydrogen atom is [1]
(a) 13.2 E
(b) 7.2 E
(c) 5.6 E
(d) 3.2 E
Answer:
(b) 7.2 E
E
3
– E
2
= E or E = -136 (\(\frac{1}{n_1^2}\) – \(\frac{1}{n_2^2}\))
= E
1
(\(\frac{1}{n_1^2}\) – \(\frac{1}{n_2^2}\))
\(\frac{E_1}{9}\) – \(\frac{E_1}{4}\) = E
or E
1
= -7.2 E
∴ Ionisation energy of hydrogen is 7.2 E.
For questions 13 to 16 two statements are given-one labelled
Assertion (A) and other labelled Reason (R).
Select the correct answer to these questions from the options as given below.
(a) If both A and R are true and R is the correct explanation of A.
(b) If both A and R are true but R is not the correct explanation of A.
(c) If A is true but R is false.
(d) If both A and R are false.
Question 13.
Assertion (A) The energy and momentum of a photon are related by p = \(\frac{ E }{ c }\).
Reason (R) The photon behaves like a particle. [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
As we know, momentum of a photon is given by
p = \(\frac{ h }{ λ }\), where the photon is a form of energy packets behaves as a particle having energy E = \(\frac{ hc }{ λ }\), so
p = \(\frac{ E }{ c }\)
Question 14.
Assertion (A) The number of electrons in a p-type silicon semiconductor is less than the number of electrons in a pure silicon semiconductor at room temperature.
Reason (R) It is due to law of mass action. [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
As we know, in intrinsic semiconductor,
n
i
= n
e
= n
h
and for p-type semiconductor, n
e
would be less than n
i
because of law of mass action as
n
i
i
= n
e
n
h
.
Question 15.
Assertion (A) The quantity L/R possesses dimensions of time.
Reason (R) To reduce the rate of change of current through a solenoid should increase the time constant (L/R). [1]
Answer:
(b) If both A and R are true but R is not the correct explanation of A.
Induced emf is given by | e| = \(\frac{ L dl }{ d t }\)
where, current I = \(\frac{ e }{ R }\)
I = \(\frac{ 1 }{ R }\) . \(\frac{ L dl }{ d t }\)
\(\frac{ d l }{ d t }\) = I . \(\frac{ R }{ L }\) = \(\frac{ I }{ \frac{ L }{ R } }\)
To decrease the rate of change in current through solenoid, we have to increase the value of time constant \(\frac{ L }{ R }\).
Question 16.
Assertion (A) A double convex lens (μ = 1.5) has focal length 10 cm. When the lens is immersed in water (μ = \(\frac{ 4 }{ 3 }\)) focal length becomes 40 cm.
Reason (R) \(\frac{1}{f}\) = \(\frac{\mu_l-\mu_m}{\mu_m}\) (\(\frac{1}{R_1}\) – \(\frac{1}{R_2}\)) [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
Given,
\(\mu_{\text {lens }}\) = 1.5, \(f_{\text {air }}\) = 10 cm
\(\mu_W\) = \(\), \(f_{\text {water }}\) = 40 cm.

Section B
Question 17.
Assuming an ideal diode, draw the output waveform for the circuit given in the figure. Explain the waveform. [2]
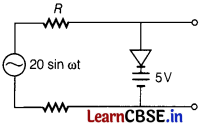
Answer:
When the input voltage is equal to or less than 5 V, diode will be reverse biased. It will offer high resistance in comparison to resistance (R) in series. Now, diode appears in open circuit. The input /waveform is then passed to the output terminals. The result with sine wave input is to dip off all positive going portion above 5 V.
If input voltage is more than + 5 V, diode will be conducting as if forward biased offering low resistance in comparison to R. But there will be no voltage in output beyond 5 V as the voltage beyond + 5 V will appear across R.
When input voltage is negative, if there will be opposition to 5 V battery. In p-n junction, if input voltage becomes more than – 5 V, the diode will be reverse biased. It will offer high resistance in comparison to resistance R in series. Now, junction diode appears in open circuit. The input waveform is then passed on to the output terminals.
The output waveform is shown here in the figure
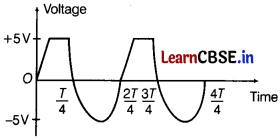
Question 18.
(i) The photoelectric current at distances r
1
and r
2
of light source from photoelectric cell are I
1
and I
2
, respectively find the value of \(\frac{I_1}{I_2}\) . [1]
(ii) If the frequency of incident radiation is equal to the threshold frequency, what will be the value of stopping potential? [1]
Answer:
(i) Since, I ∝ \(\frac{ 1 }{ r ^2 }\)
So, \(\frac{I_1}{I_2}\) = \(\left(\frac{r_2}{r_1}\right)^2\)
(ii) We know that,
max =eV
0
= h(v V
0
)
Here, v = v
0
∴ eV
0
= h (v
0
– v
0
) ⇒ eV
0
= 0
∴ V
0
=0
Hence, stopping potential becomes zero when frequency of incident radiation is equal to threshold frequency.
Question 19.
A ray of light suffers minimum deviation, while passing through a prism of refractive index 1.5 and refracting angle 60°.
Calculate the angle of deviation and angle of incidence. [2]
[Given, sin
-1
(0.75) = 48.6°]
Answer:
Given, refractive index, μ = 1.5
Angle of prism, A = 60°, angle of deviation, δ
m
=?
Angle of incidence, i = ?

Question 20.
(i) Describe how the resistivity of the conductor depends upon
(a) number density (n) of free electrons and
(b) relaxation time (τ). [1]
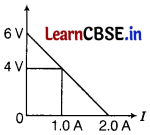
(ii) The figure shows a plot of terminal voltage V versus the current i of a given cell.
Calculate from the graph
(a) emf of the cell.
(b) internal resistance of the cell. [1]
Answer:
(i) Resistivity of a conductor is given by ρ =
(a) Resistivity ρ ∝ \(\frac{1}{n}\), where n is the number density of free electrons.
(b) Resistivity ρ ∝ \(\frac{1}{τ}\), where T is the relaxation time.
(ii) V = E – ir
(a) When i = 0, then V = E.
When i = 0, then V = 6V (from the graph)
∴ emf of the cell (E) = 6V
(b) When i = 2A, then V = 0 (from the graph)
E = ir
⇒ r = \(\frac{E}{i}\) = \(\frac{6}{2}\) = 3Ω
Question 21.
Show that spherical mirror formula is applicable to a plane mirror. [2]
Or
An infinitely long rod lies along the axis of concave mirror of focal length f. The near end of the rod is at a distance x > f from the mirror f, then what will be the length of the image of the rod? [2]
Answer:
The spherical mirror formula is given by
\(\frac{1}{u}\) + \(\frac{1}{v}\) = \(\frac{1}{f}\) ………(i)
For a plane mirror, R = ∞
∴ f = \(\frac{R}{2}\) = ∞
From Eq. (i), we get
\(\frac{1}{u}\) + \(\frac{1}{v}\) = \(\frac{1}{∞}\) = 0
⇒ \(\frac{1}{v}\) = latex]\frac{-1}{u}[/latex] ⇒ V = -u
As, u is negative, v becomes positive.
Thus, image is formed behind the mirror at the same distance as the object is in front of it. This happens in a plane mirror and hence, spherical mirror formula is applicable to plane mirror.
Also, note that magnification, m = \(-\frac{v}{u}\) is 1.
Or
Using mirror formula,
\(\frac{1}{f}\) = \(\frac{1}{v}\) + \(\frac{1}{u}\)
Here,
⇒ u = -u, v = ?, f = -f
\(-\frac{1}{f}\) = \(\frac{1}{v}\) – \(\frac{1}{u}\)
or \(\frac{1}{v}\) = \(\frac{1}{-f}\) + \(\frac{1}{u}\)
⇒ v = \(\frac{-f u}{-f+u}\)
Length of the image = \(\frac{-f u}{-f+u}\) – f
= \(\frac{f u+f^2-f u}{-f+u}\) = \(\frac{f^2}{u-f}\)
Section C
Question 22.
If both the number of protons and neutrons are conserved in a nuclear reaction like
\({ }_6 \mathrm{C}^{12}\) + \({ }_6 \mathrm{C}^{12}\) → \({ }_{10} \mathrm{Ne}^{20}\) + \({ }_2 \mathrm{He}^4\)
In what way is the mass converted into energy? Explain. [3]
Answer:
The sum of masses of nuclei of product element is less than sum of masses of reactants and hence, loss of mass takes place during the reaction. This difference of mass of product element and reactant is converted into energy and liberated in the form of heat.
Here, sum of masses of \({ }_{10} \mathrm{Ne}^{20}\) and \({ }_2 \mathrm{He}^4\) is less than the sum of two \({ }_6 \mathrm{C}^{12}\) and conversion of this mass defect is used to produce energy.
Question 23.
Use Gauss’ law to derive the expression for the electric field between two uniformly charged parallel sheets with surface charge densities σ and -σ, respectively. [3]
Answer:
Let us consider two uniformly charge parallel sheets carrying surface charge densities + σ and – σ respectively and are separated by a small distance from each other.
By Gauss’ law, it can be proved that, electric field intensity due to a uniformly charged infinite plane
sheet as nearby is given by E = \(\frac{\sigma}{2 \varepsilon_0}\)
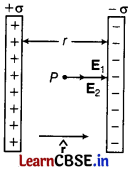
The electric field is directed normally outward from the plane sheet, if nature of charge on sheet is positive and normally inward, if charge is of negative nature. Let \(\hat{r}\) represents unit vector directed from positive plate to negative plate.
Now, electric field intensity (EFI) at any point P between the two plates is given by
(i) E
1
= + \(\frac{\sigma}{2 \varepsilon_0}\) \(\hat{r}\) [due to positive plate]
(ii) E
2
= + \(\frac{\sigma}{2 \varepsilon_0}\) \(\hat{r}\) [due to negative plate]
∴ New EFI at point P,
E = E
1
+ E
2
= \(\frac{\sigma}{2 \varepsilon_0}\) \(\hat{r}\) + \(\frac{\sigma}{2 \varepsilon_0}\) \(\hat{r}\) = \(\frac{\sigma}{\varepsilon_0}\) \(\hat{r}\)
Thus, uniform electric field is produced between the two infinite parallel plane sheet of charge which is directed from positive plate to negative plate.
Question 24.
An electron, α-particle and a proton have the same de-Broglie wavelengths. Which of these particle has [3]
(i) minimum kinetic energy?
(ii) maximum kinetic energy and why?
In what way has the wave nature of electron beam exploited in electron microscope?
Answer:
de-Broglie matter wave equation,
λ = \(\frac{h}{p}\) = \(\frac{h}{\sqrt{2 m K}}\) [∵ K = \(\frac{p^2}{2 m}\)]
where, K is kinetic energy and m is mass of particle.
K = \(\frac{h^2}{2 m \lambda^2}\) [for same wavelength λ]
⇒ K ∝ \(\frac{1}{m}\) ⇒ K
e
> K
p
> K
α
= \(\frac{1}{m_e}\) : \(\frac{1}{m_α}\) : \(\frac{1}{m_p}\)
where, m
e
, m
p
and m
α
are masses of electron, proton and α-particle, respectively.
Also, K
e
, K
p
and K
α
are their respective kinetic energies.
∵ m
α
> m
p
> m
e
⇒ K
e
> K
p
> K
α
(i) α-particle possesses minimum kinetic energy.
(ii) Electron has maximum kinetic energy.
The magnifying power of an electron microscope is inversely related to wavelength of radiation used. Smaller wavelength of electron beam in comparison to visible light increases the magnifying power of microscope.
Question 25.
Ten identical cells each of emf 2 V and internal resistance 1Ω are connected in series with two cells wrongly connected. A resistor of 10Ω is connected to the combination. Find the value of current through resistor. [3]
Answer:
According to given situation,
Net emf, of the combination
E
net
= 8 × emf of 1 cell – 2 × emf of 1 cell.
= 8 × 2 – 2 × 2 = 12 V
Equivalent resistance of the circuit,
R’ = 10r + R
= 10 × 1 + 10 = 20 Ω
∴ Current through the resistor,
I = \(\frac{E_{\text {net }}}{R^{\prime}}\) = \(\frac{12}{20}\) = 0.6 A
Question 26.
A metallic rod of length l is moved perpendicular to its length with velocity v in a magnetic field B acting perpendicular to the plane in which rod moves. Derive the expression for the induced emf. [3]
Answer:
Consider a uniform magnetic field B confined to the region ABCD and a coil PQRS is placed inside the magnetic field. At any timet, the part P’Q = S’R = y of the coil is inside the magnetic field. Let l be the length of the arm of the coil.
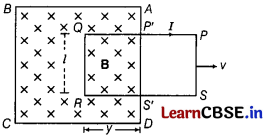
Area of the coil inside the magnetic field at time t,
∆S = QR × RS’ = ly
Magnetic flux linked with the coil at any timef,
ϕ = B∆S = Bly
The rate of change of magnetic flux linked with the coil is given by
\(\frac{d \phi}{d t}\) = \(\frac{d}{d t}\) (Blv)
= Bl \(\frac{d y}{d t}\) = Blv
where, v is the velocity with which the coil is pulled out of the magnetic field.
If e is the induced emf, then according to Faraday’s law,
e = – \(\frac{d \phi}{d t}\) or e = – Blv
From Fleming’s right hand rule, the current due to induced emf will flow from the end R toQ, i.e. along SROP in the coil. This induced electromotive force (emf) Blv is called motional emf.
Question 27.
A light bulb is rated 100 W for 220 V AC supply of 50 Hz. Calculate
(i) resistance of the bulb.
(ii) the rms current through the bulb. [3]
Answer:
(i) Power, P = EI ⇒ P = E × \(\frac{ E }{ R }\) [I = \(\frac{ E }{ R }\)]
⇒ R = \(\frac{ E^2 }{ R }\) = \(\frac{ (220)^2 }{ 100 }\) = \(\frac{ 48400 }{ 100 }\) = 484 Ω
(ii) The peak voltage of the source is E
rms
= \(\frac{ E_0 }{ \sqrt{2} }\)
⇒ E
0
= E
rms
× \(\sqrt{2}\) = 220√2 = 311.13V
∴ I
rms
= \(\frac{ I_0 }{ \sqrt{2} }\) = \(\frac{ E_0 }{R \sqrt{2} }\) = \(\frac{311.13}{484 \sqrt{2}}\) = \(\frac{311.13}{684.479}\) = 0.45 A
Question 28.
(i) What do you mean by threshold wavelength? [1]
(ii) A 60 W source emits monochromatic light of wavelength 662.5 nm. Find the value of number of photons emitted per second. [2]
Or
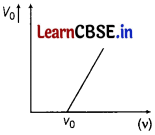
In an experiment, to study photoelectric effect, the observed variation of stopping potential with frequency of incident radiation is shown in figure. Find the value of slope and the value of y-intercept. [3]
Answer:
(i) The maximum wavelength which can emit the electron from metal surface and above which, emission of photoelectrons is not possible, called threshold wavelength.
(ii) Given, P = 60 W
λ = 662.5 nm
= 6625 × 10
-7
m
Energy of 1 photon = hv = h\(\frac{c}{λ}\)
= 6625 × 10
-34
× \(\frac{3 \times 10^8}{6625 \times 10^{-7}}\)
= 3 × 10
-19
J
∴ Number of photons emitted per second = \(\frac{\text { Power of source }}{\text { Energy of one photon }}\)
= \(\frac{60}{3 \times 10^{-19}}\) = 20 × 10
19
= 2 × 10
20
Or
We know that maximum kinetic energy of emitted photoelectrons,
K
max
= hv – ϕ
0
⇒ eV
0
= hv – ϕ
0
⇒ V
0
= \(\left(\frac{h}{e}\right) v\) = \(\frac{\phi_0}{e}\)
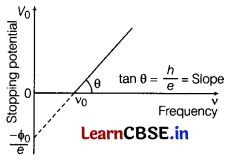
Comparing with y = mx + c, we get
m = \(\frac{h}{e}\) and c = \(-\frac{\phi_0}{e}\) = \(-\frac{h v_0}{e}\)
Slope = m = \(\frac{h}{e}\)
and y -intercept = c = \(-\frac{h v_0}{e}\)
Section D
[Case Study Based Questions]
Question 29.
Read the following paragraph and answer the questions that follows.
Mirror formula is a relation between focal length, distance of object and distance of image from the mirror. The
mirror formula is given by \(\frac{ 1 }{ f }\) = \(\frac{ 1 }{ u }\) + \(\frac{ 1 }{ v }\)
where, u is the distance of object v is the distance of image and f is the focal length.
Focal length of the mirror, f = \(\frac{ R }{ 2 }\)
\(\frac{ 1 }{ u }\) + \(\frac{ 1 }{ v }\) = \(\frac{ 1 }{\frac{ R }{ 2 }}\)
\(\frac{ 1 }{ u }\) + \(\frac{ 1 }{ v }\) = \(\frac{ 2 }{ R }\)
Moreover, lens formula is given by
\(\frac{ 1 }{ f }\) = \(\frac{ 1 }{ v }\) – \(\frac{ 1 }{ u }\)
Power of lens, P = \(\frac{ 1 }{ f(m) }\) = \(\frac{ 100 }{ f(cm) }\)
(i) A convex lens is formed from a spherical surface of radius 20 cm. The power of lens is [1]
(a) 10D
(b) -10 D
(c) 5D
(d) -5D
Answer:
(a) 10D
Given, R = 20 cm
Focal length, f = \(\frac{ R }{ 2 }\) = \(\frac{ 20 }{ 2 }\) = 10 cm = 0.1 m
Power of the lens, P = \(\frac{ R }{ f }\) = \(\frac{ 1 }{ 0.1 }\) = + 10 D
(ii) Power of concave lens is [1]
(a) positive
(b) negative
(c) 1
(d) -1
Answer:
(b) negative
Focal length of concave lens is negative
∴ P = \(\frac{1}{f}\) = negative
(iii) A point object is placed at a distance of 30 cm from a convex mirror of focal length 30 cm. The image will form at [1]
(a) infinity
(b) pole
(c) focus
(d) 15 cm behind the mirror
Answer:
(d) 15 cm behind the mirror
Given, u = – 30 cm and f = 30 cm
\(\frac{1}{v}\) + \(\frac{1}{-30}\) = \(\frac{1}{30}\)
⇒ \(\frac{1}{v}\) = \(\frac{1}{30}\) + \(\frac{1}{30}\)
∴ Distance from the mirror, v = + 15 cm.
Or
Which mirror forms always a virtual image? [1]
(a) Convex
(b) Concave
(c) Both (a) and (b)
(d) None of these
Answer:
(a) Convex
Convex mirror forms always a virtual and diminished image.
(iv) An object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is [1]
(a) real, inverted and same size
(b) real, inverted and smaller in size
(c) virtual, erect and larger in size
(d) virtual, erect and smaller in size
Answer:
(a) real, inverted and same size
Image formed is real, inverted and same in size because object is at the centre of curvature of the mirror.
Question 30.
Read the following paragraph and answer the questions that follows.
Semiconductor
In an n-type semiconductor, the concentration of electrons is more than that of holes. Similarly in a p-type semiconductor, the concentration of holes is more than that of electrons. During the formation of p-n junction and due to the concentration gradient across p-type and n-type, holes diffuse from p-sides to n -side and electron diffuse from n-side to p-side.
(i) The expected energy of the electron at absolute zero is called [1]
(a) fermi energy
(b) emission energy
(c) work function
(d) potential energy
Answer:
(a) fermi energy
The expected energy of the electron at absolute zero is called fermi energy
(ii) In the depletion region of a unbiased p-n junction diode, there are [1]
(a) only electrons
(b) only holes
(c) both electrons and holes
(d) only fixed ions
Answer:
(d) only fixed ions
In the depletion region of a unbiased p-n junction diode, all the electrons and holes are combine together from both sides, hence only ions are present in depletion region.
(iii) In forward bias, the width of the potential barrier in a p-n junction diode [1]
(a) increases
(b) decreases
(c) remains constant
(d) first increases then decreases
Answer:
(b) decreases
In forward bias, the width of the potential barrier in a p-n junction diode is decrease.
(iv) A reverse baised diode is
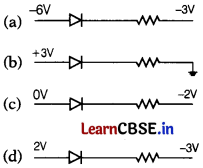
Answer:
![]()
As, – 6V < – 3V
i.e. p is at low potential than n diode is reverse
![]()
Or
The p-n junction diode is used as [1]
(a) an amplifier
(b) a rectifier
(c) an oscillator
(d) a modulator
Answer:
(b) a rectifier
The p-n junction diode is used as a rectifier.
Section E
Question 31.
(i) (a) A mobile phone lies along the principal axis of a concave mirror. Show with the help of a suitable diagram the formation of its image. Explain, why magnification is not uniform?
(b) Suppose the lower half of the concave mirror’s reflecting surface is covered with an opaque material. What effect this will have on the image of the object? Explain. [3]
(ii) (a) A concave mirror of small aperture forms a sharper image. Why?
(b) A lens of refractive index \(\frac{3}{2}\) is immersed in water of refractive index \(\frac{4}{3}\). Determine the percentage change in its focal length.
Answer:
(i) (a) The ray diagram for the formation of the image of the mobile phone is shown below. The image of the part which is on the plane perpendicular to principal axis will be on the same plane. It will be of the same size only at C.
i.e., B’C = BC.
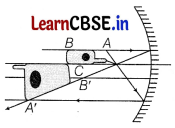
Here, magnification of each part of the mobile phone can’t be uniform due to different locations of phone.
(b) We may think that the image will now show only half of the object, but considering the laws of reflection to be true for all points of the remaining part of the mirror, the image will be that of the whole object.
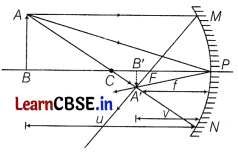
However, as the area of the reflecting surface has been reduced, the intensity of the image will be low, i.e. half.
(ii) (a) The rays of light travelling parallel to the principal axis, after reflection from a concave mirror meet at a single point only, If the beam of light is narrow or if the mirror is of small aperture. In case, a wide beam of light falls on a concave mirror of large aperture, the rays after reflection from the mirror do not come to focus at a single point. Therefore, it follows that, if the aperture of the concave mirror is small, the image formed will be sharper.
(b) Given, \({ }^a \mu_g\) = \(\frac{3}{2}\), \(f_{\text {air }}\) = f
\({ }^a \mu_w\) = \(\frac{4}{3}\)
Using lens Maker’s formula, when lens is in air,

Or
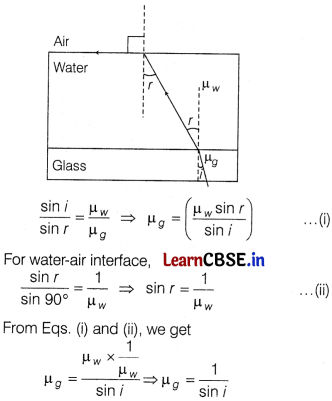
(i) A ray of light is incident at a glass-water interface at an angle of i, it emerges finally surface water, then what will be the value of μ
g
? [1]
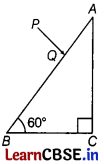
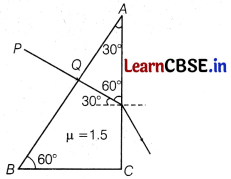
(ii) A ray PQ incident normally on the refracting face BA is refracted in the prism BAC made of material of refractive index 1.5. Complete the path of ray through the prism. From which face will the ray emerge?
Justify your answer. [3]
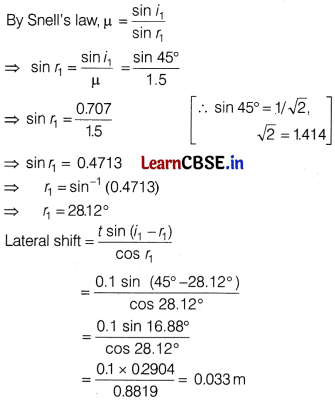
(iii) A ray of light is incident at an angle of 45° on one face of a rectangular glass slab of thickness 10 cm and refractive index 1.5. Calculate the lateral shift produced. [1]
Answer:
(i) For glass-water interface, applying Snell’s law,
(ii) Given, refractive index of the material of the prism, μ =1.5
Critical angle for the material,
sin C = \(\frac{1}{\mu}\) = \(\frac{1}{1.5}\) = 2/3
⇒ C = sin
-1
(\(\frac{2}{3}\)) ≃ 42°
From the ray diagram, it is clear that angle of incidence i = 30° < C.
Therefore, the ray incident at the face AC will not suffer total internal reflection and emerges out through this face.
(iii) Given, i
1
= 45°, t = 10 cm = 0.1m, p =1.5
Lateral shift = ?
Question 32.
Three concentric metal shells A, B and C of radius a, b and c (a < b< c) have surface charge densities + σ, – σ and + σ, respectively.
(i) Find the potential of three shells at A, B and C. [2]
(ii) If the shells A and C are at the same potential, obtain the relation between the radii a, b and c. [3]
Answer:
(i) At shell A
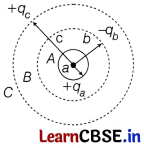

(ii) Relation between the radii
Now, V
A
= V
C
(given)
\(\frac{\sigma}{\varepsilon_0}\) (a – b + c) = \(\frac{\sigma}{\varepsilon_0}\) \(\frac{\left(a^2-b^2+c^2\right)}{c}\)
a – b + c = \(\frac{a^2-b^2+c^2}{c}\) = \(\frac{a^2-b^2}{c}\) + c
c(a – b) = a² – b²
⇒ c = a + b
[∵ (a² – b² = (a – b) (a + b)]
Or
Two metal spheres, one of radius R and the other of radius 2R, both have same surface charge density a. They are brought in contact and separated. What will be new surface charge densities on them? [5]
Answer:
Radius of sphere A = R
Surface charge density on sphere A = σ
Radius of sphere B = 2R
Surface charge density on sphere B = a
Before contact, the charge on sphere A,
Q
1
= Surface charge density × Surface area
⇒ Q
1
= σ . 4πR² …(i)
Before contact, the charge on sphere B,
Q
2
= Surface charge density × Surface area
Q
2
= σ . 4π(2R)² = C-16πR² …(ii)
Let after the contact, the charge on A be Q’
1
and the charge on B be Q’
2
.
According to the conservation of charge, the charge before contact is equal to charge after contact.
Q’
1
+ Q’
2
= Q
1
+ Q
2
Now, from Eqs. (i) and (ii), we get
Q’
1
+ Q’
2
= 4πR²σ + 16πR²σ
= 20πR²σ …(iii)
As they are in contact, so they have same potential.
Potential on sphere A, V
A
= \(\frac{1}{4 \pi \varepsilon_0}\) ⋅ \(\frac{Q_1^{\prime}}{R}\)
Potential on sphere B , V
B
= \(\frac{1}{4 \pi \varepsilon_0}\) ⋅ \(\frac{Q_2^{\prime}}{2 R}\)
So, V
A
= V
B
⇒ \(\frac{1}{4 \pi \varepsilon_0}\) . \(\frac{Q_1^{\prime}}{R}\) = \(\frac{1}{4 \pi \varepsilon_0}\) . \(\frac{Q_2^{\prime}}{2 R}\)
⇒ \(\frac{Q_1^{\prime}}{R}\) = \(\frac{1}{4 \pi \varepsilon_0}\) ⋅ \(\frac{Q_2^{\prime}}{2 R}\)
⇒ 2Q’
1
= Q’
2
……(iv)
Putting the value of 02 in Eq. (iii), we get
Q’
1
+ 2Q’
1
= 20πR²σ
⇒ 3Q’
1
= 20πR²σ
⇒ Q’
1
= \(\frac{20}{3}\) πR²σ
and Q’
2
= \(\frac{40}{3}\) πR²σ [from Eq. (iv)]
Let the new charge densities be σ
1
and σ
2
.

Thus, the surface charge densities on spheres after contact are \(\frac{5}{3}\) cr and \(\frac{5}{6}\) a.
Question 33.
A device X is connected to an AC source, V =V
0
sin ωt. The variation of voltage, current and power in one cycle is shown in the following graph.
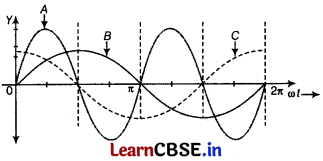
(i) Identify the device X. [1]
(ii) Which of the curves A, B and C represent the voltage, current and the power consumed in the circuit?
Justify the answer. [1]
(iii) How does its impedance vary with frequency of the AC source? Show graphically. [2]
(iv) Obtain an expression for the current in the circuit and its phase relation with AC voltage. [1]
Answer:
(i) Device X is a capacitor.
As, the current is leading voltage by \(\frac{\pi}{2}\) rad.
(ii) As, E(t) = E
0
sin ωt
Current, I(t) = I
0
cos ωt
As, in the case of capacitor,
I = I
0
sin (ωt + \(\frac{\pi}{2}\)) [current is leading voltage]
Average power, P = E(t) I(t) = E
0
I
0
cos ϕ /2
where, ϕ = phase difference
Hence, curve A represents power, curve B represents voltage and curve C represents current.
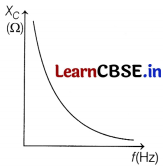
(iii) As, X
C
= capacitive reactance = \(\frac{1}{C \omega}\)
where, ω is angular frequency.
X
C
= \(\frac{1}{2}\)
So, reactance or impedance decreases with increase in frequency. Graph of X
C
versus f is shown below
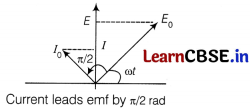
(iv) As given, V = V
0
sin ωt
Also, we know that
Q = CV
I = \(\frac{d Q}{d t}\) = \(\frac{d(C V)}{d t}\) = \(\frac{C d\left(V_0 \sin \omega t\right)}{d t}\)
I = \(\frac{C V_0 d(\sin \omega t)}{d t}\) = CV
0
ω cos ωt
I = I
0
sin(ω + π/2)
Thus, there is a phase difference between current and voltage is \(\frac{\pi}{2}\).
Or
The given circuit diagram shows a series L-C-R circuit connected to a variable frequency 230 V source.
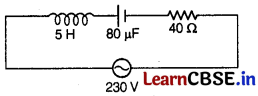
(i) Determine the source frequency which derives the circuit in resonance.
(ii) Obtain the impedance of the circuit and the amplitude of current at the resonating frequency. [1]
(iii) Determine the rms potential drop across the three elements of the circuit. [2]
(iv) How do you explain the observation that the algebraic sum of the voltage across the three elements in capacitance (C) is greater than the supplied voltage? [1]
Answer:
Given, L = 5.0H, C = 80 μF = 80 × 10
-6
F,
R = 40 Ω and V
rms
= 230 V
