Students must start practicing the questions from CBSE Sample Papers for Class 12 Physics with Solutions Set 8 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Physics Set 8 with Solutions
Time : 3 hrs
Max. Marks : 70
Instructions
1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary.
(i) c = 3 × 10
8
m/s
(ii) m
e
= 9.1 × 10
-31
kg
(iii) e = 1.6 × 10
-19
C
(iv) µ
0
= 4π × 10
-7
TmA× 10
-1
(v) h = 6.63 × 10
-34
Js
(vi) ε
0
= 8.854 × 10
-112
C
2
N
-1
m
-2
(vii) Avogadro’s number = 6.023 × 10
23
per gram mole
Section A
Question 1.
Two capacitors C
1
and C
2
are charged to 120 V and 200 V, respectively. It is found that by connecting them together, the potential on each one of them can be made zero. Then, [1]
(a) 5 C
1
= 3 C
2
(b) 3 C
1
= 5 C
2
(c) 3 C
1
± 5 C
2
= 0
(d) 9 C
1
= 4 C
2
Answer:
(c) 3 C
1
± 5 C
2
= 0
Potential on each capacitor can be made zero, if q
net
= 0.
⇒ q
1
± q
2
= o
⇒ 120 C
1
± 200 C
2
= 0 [∵ q = CV]
⇒ 3C
1
± 5C
2
= 0
Question 2.
A wire AB carrying a steady current of 12 A and is lying on the table. Another wire CD carrying 5 A is held directly above AB at a height of 1 mm. The mass per unit length of the wire CD, so that it remains suspended at its position when left free is (Take, g = 10 m/s
2
) [1]
(a) 1 × 10
-3
kg/m
(b) 2 × 10
-3
kg/m
(c) 1.2 × 10
-3
kg/m
(d) 22 × 10
-3
kg/m
Answer:
(c) 1.2 × 10
-3
kg/m
Force per unit length between the current-carrying wires is given as
F = \(\frac{\mu_0}{4 \pi}\) ⋅ \(\frac{2 l_1 l_2}{r}\)
where, l
1
= current in wire AB = 12 A,
l
2
= current in wire CD = 5 A
r = height above AB
= 1 mm = 1 × 10
-3
m.
∴ \(\frac{\mu_0}{4 \pi}\) ⋅ \(\frac{2 l_1 l_2}{r}\) = mg
where, m = mass per unit length.
⇒ 10
-7
× = m × 10
∴ m = 1.2 × 10
-3
kg/m
![]()
Question 3.
A proton, a neutron, an electron and an α-particle have same kinetic energy. Then, their de-Broglie wavelengths compare as [1]
(a) λ
p
= λ
n
> λ
e
> λ
α
(b) λ
α
< λ
p
= λ
n
< λ
e
(c) λ
e
< λ
p
= λ
n
> λ
α
(d) λ
e
= λ
p
= λ
n
= λ
α
Answer:
(c) λ
e
< λ
p
= λ
n
> λ
α
We know that, the relation between de-Broglie wavelength (λ) and kinetic energy (K) is given by,
λ = \(\frac{h}{\sqrt{2 m K}}\) or λ = \(\frac{1}{\sqrt{m}}\)
Since, m
p
= m
n
, hence, λ
p
= λ
n
As, m
α
> m
p
, therefore λ
α
< λ
p
As, m
e
< m
n
, therefore λ
e
> λ
n
Hence, λ
α
< λ
p
= λ
n
< λ
e
Question 4.
The figure given below shows various equipotential surfaces. [1]
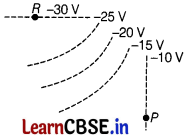
What is the direction of electric field E at P and R?
(a) At P, E is to the left and at R, E is upward
(b) At P, E is to the right and at R, E is downward
(c) At P, E is to downward and at R, E is to the left
(d) At P, E is to upward and at R, E is to the right
Answer:
(a) At P, E is to the left and at R, E is upward
Electric field lines are perpendicular to the equipotential surfaces and point in the direction of decreasing potential. So, at point P, electric field E is to the left and at point R, E is upward.
Question 5.
Which of the following is not an electromagnetic wave? [11
(a) γ-ray
(b) X-ray
(c) Heat wave
(d) β-ray
Answer:
(d) β-ray
β-ray is a radioactive radiation, whereas X-rays, γ-rays, heat waves are electromagnetic waves.
Question 6.
The radius of a nucleus of a mass number A is directly proportional to [1]
(a) A
3
(b) A
(c) A
2/3
(d) A
1/3
Answer:
(d) A
1/3
Radius of nucleus, R = R
0
A
1/3
where, R
0
is a constant and A is the mass number.
Question 7.
Two coils X and Y are placed in a circuit such that when the current changes by 2 A in coil X. The magnetic flux changes by 0.4 Wb in Y. The value of mutual inductance of the coils is [1]
(a) 0.2 H
(b) 5 H
(c) 0.8 H
(d) 4 H
Answer:
(a) 0.2 H
We have, M = \(\frac{\Delta \phi_2}{\Delta I_i}\)
∴ Mutual inductance of the coil, M = \(\frac{0.4}{2}\) => 0.2 H
Question 8.
The net magnetic flux through any closed surface kept in a magnetic field [1]
(a) zero
(b) \(\frac{\mu_0}{4 \pi}\)
(c) 4π μ
0
(d) \(\frac{4 \mu_0}{\pi}\)
Answer:
(a) zero
According to Gauss law in magnetism, surface integral of magnetic field intensity over a surface (closed or open) is always zero i.e. \(\oint B \cdot d A\) = 0
Question 9.
In figure given below, V
0
is the potential barrier across a p-n junction, when no battery is connected across the junction, then [1]

(a) 1 and 3 both correspond to forward bias of junction
(b) 3 corresponds to forward bias of junction and 1 corresponds to reverse bias of junction
(c) 1 corresponds to forward bias and 3 corresponds to reverse bias of junction
(d) 3 and 1 both correspond to reverse bias of junction
Answer:
(b) 3 corresponds to forward bias of junction and 1 corresponds to reverse bias of junction
When p-n junction is forward biased, it opposes the potential barrier junction, when p-n junction is reverse biased, it supports the potential barrier junction, resulting in increase in potential barrier across the junction.
So, 3 corresponds to forward bias of junction and 1 corresponds to reverse bias of junction.
![]()
Question 10.
Particles which can be added to the nucleus of an atom without changing its chemical properties are called [1]
(a) neutrons
(b) electrons
(c) protons
(d) alpha particles
Answer:
(c) protons
Chemical properties are unaffected with addition of neutrons to the nucleus.
Question 11.
A circular coil of 20 turns and radius 10 cm is placed in uniform magnetic field of 0.10 T, normal to the plane of the coil. If the current in coil is 5 A, then the torque acting on the coil will be [1]
(a) 31.4 N-m
(b) 3.14 N-m
(c) 0.314 N-m
(d) zero
Answer:
(d) zero
Given, number of turns, N = 20
Radius of coil, r = 10cm= 10 × 10
-2
m
Magnetic field, 6 = 0.10T
Current, I = 5A
Angle between field and normal to the coil, θ = 0°
∵ Area of Coil, A = πr²
= π(10 × 10
-2
)
2
= π × 10
-2
m
2
∴ Torque, τ = BINA sin θ
= 20 x 5 x 0.10 x n x 10-2 sin 0°
= 0 {∵ sin 0°= 0 }
Question 12.
A proton of energy 8 eV is moving in a circular path in uniform magnetic field. The energy of an alpha particle moving in same magnetic field and along same path will be [1]
(a) 4 eV
(b) 2 eV
(c) 8 eV
(d) 6 eV
Answer:
(c) 8 eV
We know that, Bqv = \(\frac{mv^2}{r}\)

For questions 13 to 16 two statements are given-one labelled
Assertion (A) and other labelled Reason (R).
Select the correct answer to these questions from the options as given below.
(a) If both A and R are true and R is the correct explanation of A.
(b) If both A and R are true but R is not the correct explanation of A.
(c) If A is true but R is false.
(d) If both A and R are false.
Question 13.
Assertion (A) The alternating current lags behind the electromotive force by the phase angle of \(\frac{\pi}{2}\), when AC flows through an inductor.
Reason (R) The inductive reactance increases as the frequency of AC source decreases. [1]
Answer:
(c) If A is true but R is false.
When pure inductor is connected to source of an alternating emf, then instantaneous value of
alternating current is given by I = I
0
sin(ωt – \(\frac{\pi}{2}\)).
Inductive resistance, X
L
= coL = 2πfL.
When frequency is increased, then inductive resistance is increased.
![]()
Question 14.
Assertion (A) At resonance, in LCR series combination, the current value is maximum.
Reason (R) At resonance, in LCR series circuit, the current and emf are in phase with each other. [1]
Answer:
(b) If both A and R are true but R is not the correct explanation of A.
In LCR series circuit, at resonance X
L
= X
C
Thus, Z = \(\sqrt{R^2+\left(X_L-X_C\right)^2}\) = \(\sqrt{R^2+0}\) = R
Z
min
= R
I
max
= \(\frac{V}{Z_{\min }}\) = \(\frac{V}{R}\)
and power factor,
cos ϕ = \(\frac{R}{Z}\) = \(\frac{R}{R}\) = 1 = cos 0° ⇒ ϕ = 0
Thus, At resonance, current is maximum and emf and current are in phase with each other.
Question 15.
Assertion (A) Photosensitivity of a metal is high, if its work function is small.
Reason (R) Work function =hv
0
, where v
0
is the threshold frequency. [1]
Answer:
(b) If both A and R are true but R is not the correct explanation of A.
Work function is the minimum energy required to eject the photoelectron from photosensitive metal. Hence, for metal to be photosensitive, the work function should be small.
Work function = hv
o
, where v
0
is the threshold frequency.
Question 16.
Assertion (A) If optical density of a substance is more than that of water, then the mass density of substance can be less than water.
Reason (R) Optical density and mass density are not related. [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
Optical density and mass density are not related to each other. Mass density is mass per unit volume. Optical density is the ratio of the speed of light in two medium.
Section B
Question 17.
A system consists of two large thin metal plates held parallel and close to each other as shown in figure.
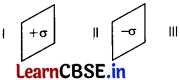
The electric field in region II is 3 × 10
-10
N/C. Calculate the value of surface density (in magnitude). [2]
Answer:
Electric field in the region II between the plates is given by
E = \(\frac{\sigma}{\varepsilon_0}\) = σ = Eε
0
= 3 × 10
-10
× 8.85 × 10
-12
⇒ a = 2.65 × 10
-21
Cm
-2
Question 18.
In the figure shown below, +Q charge is located at one of the edge of the cube. Then, what is electric flux through cube due to +Q charge? [2]
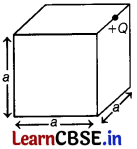
Answer:
Since, electric lines of force passes only through the four faces of cube. So, electric flux in accordance with Gauss’ law is given by,
ϕ = \(\frac{1}{4}\)(\(\frac{q_{\text {enclosed }}}{\varepsilon_0}\)) = \(\frac{+Q}{4 \varepsilon_0}\)
Question 19.
Electromagnetic waves travel in a medium with a speed of 2 × 10
8
ms
-1
. The relative magnetic permeability of the medium is 1. Find the relative electrical permittivity. [2]
Answer:
Given, v = 2 × 10
8
ms
-1
and μr=1
The speed of electromagnetic waves in a medium is given by,
v = \(\frac{1}{\sqrt{\mu \varepsilon}}\)
where, μ and ε are absolute permeability and absolute permittivity of the medium, respectively.
Now, μ = μ
0
μ
r
and ε = ε
0
ε
r

Question 20.
The focal length of a thin bi-convex lens is 20 cm. When an object is moved from a distance of 25 cm infront of it to 50 cm, the magnification of its image changes from m25 to m50. Find the ratio of m25/m50. [2]
Answer:
Since, magnification, m = \(\frac{f}{f+u}\)
m 25 = \(\frac{25}{20-25}\) = -4
m 50 = \(\frac{50}{20-50}\) = \(\frac{-2}{3}\)
Therefore, \(\frac{m_25}{m_50}\) = (-4)(-\(\frac{3}{2}\)) = 6
Question 21.
The objective of an astronomical telescope has a diameter of 150 mm and a focal length of 4 m. The eyepiece has a focal length of 25 mm Calculate the magnifying and resolving power of telescope
(λ = 6000 Å for yellow colour). [2]
Or
An equiconvex lens of focal length f is cut into two equal halves in thickness. What is the focal length of each half ? [2]
Answer:
The diameter of objective of the telescope
= 150 × 10
-3
m, f
0
= 4 m
f
e
= 25 × 10
-3
m and D = 0.25 m

Or
Focal length can be given as, \(\frac{1}{2}\) = (μ – 1) (\(\frac{1}{R_1}\) – \(\frac{1}{R_2}\))
where, μ is the refractive index of the lens medium.
R
1
and R
2
are radii of curvature.

Equiconvex lens have the same radius of curvature

Hence, focal length of each half becomes twice of the original value.
![]()
Section C
Question 22.
Explain, how Biot-Savart’s law enables one to express the Ampere’s circuital law in the integral form, viz.
\(\oint \mathbf{B} \cdot d \mathbf{l}\) = μ
0
I
where, I is the total current passing through the surface. [3]
Answer:
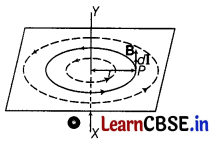
Consider any arbitrary closed path perpendicular to the plane of paper around a long straight conductor XY carrying current from X to V, lying in the plane of paper.
Let the closed path be made of large number of small elements, where
AB = dl
1
, BC =dl
2
, CD = dl
3
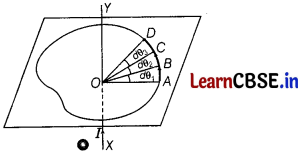
Let d θ
1
, d θ
2
, d θ
3
, be the angles subtended by the various elements at point O through which conductor is passing. Then
Let d θ
1
+ d θ
2
+ d θ
3
… = 2π
Suppose these small elements AB, BC, CD are small circular arcs of radii r
1
, r
2
, r
3
respectively.
Then d θ
1
= \(\frac{d \mathbf{I}_1}{r_1}\), d θ
2
= \(\frac{d \mathbf{I}_2}{r_2}\), d θ
3
= \(\frac{d \mathbf{I}_3}{r_3}\)
If B
1
, B
2
, B
3
are the magnetic field inductions at a point along the small elements dl
1
,dl
2
, dl
3
,
then from Biot-Savart’s law we know that for the conductor of infinite length, magnetic field is given by
B
1
= \(\frac{\mu_0}{4 \pi}\) ⋅ \(\frac{2 l}{r_1}\),
B
2
= \(\frac{\mu_0}{4 \pi}\) ⋅ \(\frac{2 l}{r_2}\),
B
3
= \(\frac{\mu_0}{4 \pi}\) ⋅ \(\frac{2 l}{r_3}\)
In case of each element, the magnetic field induction B and current element vector d I are in the same direction.
Line integral of B around closed path is

which is an expression of Ampere’s circuital law.
Question 23.
(i) For a coherent source, initial phase difference between two sources must have same finite value. Justify. [1]
(ii) Write the expression for intensity of interference and show
I
R
= I
1
+ I
2
+ 2 \(\sqrt{I_1 I_2}\) cos ϕ. [2]
Answer:
(i) If two source have constant phase difference i.e. the phase difference between two waves does not change with respect to time and frequencies should be equal. They are coherent sources of waves.
(ii) Suppose the displacements of two waves from two coherent sources S
1
and S
2
at point P,
y
1
= a
1
sin ωt
and y
2
= a
2
sin (ωt + ϕ)
By superposition principle,
y = y
1
+ y
2
= a
1
sin ωt + a
2
sin (ωt + ϕ)
= a
1
sin ωt + a
2
sin ωt cos ϕ + a
2
cos ωt sin ϕ
y = (a
1
+ a
2
cos ϕ) sin ωt + a
2
sin ϕ cos ωt
Put a
1
+ a
2
cos ϕ = A cos θ … (i)
and a
2
sin ϕ = A sin θ …(ii)
y = A cos θ sin ωt + A sin θ cos ωt
y = A sin(ωt + θ)
From Eqs. (i) and (ii), by squaring and adding,
A
2
cos
2
0 + A
2
sin
2
0 = (a
1
+ a
2
cos ϕ)
2
+ a
2
2
sin
2
ϕ
or A
2
= a
1
2
+ a
2
2
(cos
2
ϕ + sin
2
ϕ) + 2a
1
a
2
cos ϕ
or A
2
= a
1
2
+ a
2
2
+ 2a
1
a
2
cos ϕ
Intensity of wave oc (amplitude)
2
I = KA
2
KA
2
= Ka
1
2
+ Ka
2
2
+ 2 \(\sqrt{K a_1^2}\) \(\sqrt{K a_2^2}\) cos ϕ
or I = I
1
+ I
2
+ 2 \(\sqrt{I_1 I_2}\) cos ϕ
![]()
Question 24.
An electron, α-particle and a proton have the same de-Broglie wavelengths. Which of these particle has
(i) minimum kinetic energy?
(ii) maximum kinetic energy and why?
In what way has the wave nature of electron beam exploited in electron microscope?
Answer:
According to de-Broglie matter wave equation,
λ = \(\frac{h}{p}\) = \(\frac{h}{\sqrt{2 m k}}\)
where, K is kinetic energy and m is mass of the particle.
K = \(\frac{h^2}{2 m \lambda^2}\) [for same wavelength λ]
⇒ K ∝ \(\frac{1}{m}\)
⇒ K
e
: K
α
: K
p
= \(\frac{1}{m_e}\) : \(\frac{1}{m_α}\) : \(\frac{1}{m_p}\)
where, rr^, mp and ma are the masses of electron, proton and a-particle, respectively.
Also, K
e
, K
α
and K
p
are their respective kinetic energies.
∵ m
α
> m
p
> m
e
⇒ K
e
> K
α
> K
p
[∵ K = \(\frac{p^2}{2 m}\) ⇒ K ∝ \(\frac{1}{m}\)]
(i) α-particle possesses minimum kinetic energy.
(ii) Electron has maximum kinetic energy.
The magnifying power of an electron microscope is inversely related to wavelength of radiation used. Smaller wavelength of electron beam in comparison to visible light increases the magnifying power of microscope.
Question 25.
Obtain the binding energy of the nuclei I^Fe and gj9Bi in units of MeV from the following data:
m (\({ }_{26}^{56} \mathrm{Fe}\)) = 55.934939 u
m (\({ }_{83}^{209} \mathrm{Bi}\)) = 208.980388 u
Answer:
Given, m
p
= 1.00783 u, m
n
= 1.00867 u
(i) For \({ }_{26}^{56} \mathrm{Fe}\), there are 26 protons
and (56 – 26) = 30 neutrons.
Am = mass of nucleons – mass of nucleus
= 26m
p
+ 30m
p
– m
= 26 × 1.00783 + 30 × 1.00867 – 55.934939
= 0.528741 U
Total binding energy = Am × 931 MeV
= 0.528741 × 931
= 49226 MeV
Binding energy per nucleon
\(\frac{\text { Binding energy }}{\text { Number of nucleons }}\)
= \(\frac{49226}{56}\) = 8.790 MeV
(ii) For \({ }_{83}^{209} \mathrm{Bi}\),.there are 83 protons and
(209 – 83) = 126 neutrons.
Am = mass of nucleons – mass of nucleus
= 83 m
p
+ 126 m
n
– m
Am = 83 × 1.00783 + 126 × 1.00867 – 208.980388
= 1.761922 u
Binding energy = Am × 931 MeV
= 1.761922 × 931
= 1640.35 MeV
Binding energy per nucleon
\(\frac{\text { Binding energy }}{\text { Number of nucleons }}\)
= \(\frac{1640.35}{209}\) = 7.848 MeV
Thus, binding energy per nucleon of Fe is more than Bi.
Question 26.
X student wants to use two p-n junction diodes to convert AC current into DC current. Draw the labelled circuit diagram, she would use and explain how it works. [3]
Answer:
A rectifier is used to convert alternating current into direct current, whose labelled circuit is given below.
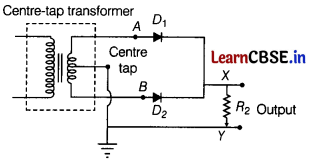
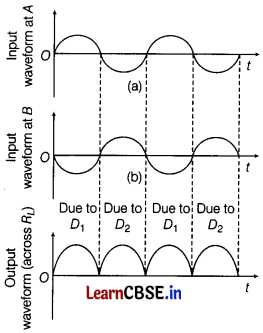
Working: During the positive half cycle of the input AC, the diode D
1
is forward biased and the diode D
2
is reverse biased. The forward current flows through diode D
1
.
During the negative half cycle of the input AC, the diode D
1
is reverse biased and diode D
2
is forward biased. Thus, current flows through diode D
2
. Thus, we find that during both the halves, current flows in the same direction.
Question 27.
Draw V-I characteristics of a p-n junction diode. Answer the following questions giving reasons.
(i) Why is the current under reverse bias almost independent of the applied potential upto a critical voltage? [1]
(ii) Why does the reverse current show a sudden increase at the critical voltage? [1]
(iii) Why energy is released, when a p-n junction diode is forward biased? [1]
Answer:
V-I characteristics of p-n junction is shown below.
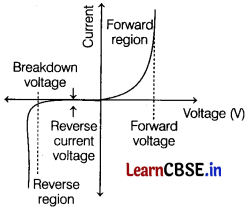
(i) Under the reverse bias condition, the holes of p-side are attracted towards the negative terminal of the battery and the electrons of the n-side are attracted towards the positive terminal of the battery. This increases the depletion layer and the induced potential barrier is also increased. However, the minority charge carriers are drifted across a junction producing a small current. At any temperature, a number of minority charge carriers is constant, so there is the small current at any applied potential. This is the reason for the current under reverse bias known as reverse saturation current which is almost independent of applied potential. At the certain level of voltage, avalanche breakdown takes place which results in a sudden flow of large current.
(ii) At the critical voltage, the voltage at which breakdown takes place, the holes in the n-side and conduction electrons in the p-side are accelerated due to the reverse bias voltage. These minority carriers acquire sufficient kinetic energy from the electric field and collide with a valence electron. Thus, the bond is finally broken and the valence electrons move into the conduction band resulting in enormous flow of electrons and thus, formation of electron-hole pairs. Thus, there is a sudden increase in the current at the critical voltage.
(iii) When p-n junction is forward biased, then energy released due to recombination of free electrons and holes.
![]()
Questions 28.
Would the Bohr’s formula for the H-atom remains unchanged, if proton had a charge (+4/3)e and electron had a charge (-3 /4)e, where e = 16 × 10
-19
C. Give reasons for your answer. [3]
Or
Positronium is just like a H-atom with proton replaced by the positively charged anti-particle of the electron (called the positron which is as massive as the electron). What would be the ground state energy of positronium? [3]
Answer:
According to Bohr’s theory, centripetal force required by the electron for its motion around the nucleus = Electric force between the proton and electron.
⇒ \(\frac{m v^2}{r}\) = \(\frac{1}{4 \pi \varepsilon_0}\) ⋅ \(\frac{\left(q_p\right)\left(q_e\right)}{r^2}\)
where, r = atomic radius,
q
p
= charge of proton = + e
q
e
= charge of electron = – e
⇒ \(\frac{m v^2}{r}\) = \(\frac{1}{4 \pi \varepsilon_0}\) ⋅ \(\frac{(e)(-e)}{r^2}\)
= \(\frac{1}{4 \pi \varepsilon_0}\) ⋅ \(\frac{-e^2}{r^2}\)
Now, given charge on proton, q
p
= + \(\frac{4}{3}\)e
Charge on electron, q
e
= – \(\frac{3}{4}\)e
Putting the new value (keeping after factors unchanged),
\(\frac{m v^2}{r}\) = \(\frac{1}{4 \pi \varepsilon_0}\)

i.e. Bohr’s formula remain unchanged.
Or
The reduced mass m of two particle system of masses mand m2 is given by \(\frac{1}{m}\) = \(\frac{1}{m_1}\) + \(\frac{1}{m_2}\).
The total energy of the electron in the stationary states of the hydrogen atom is given by
E
n
= \(-\frac{-m e^4}{8 n^2 \varepsilon_0^2 h^2}\)
where signs are as usual but m is the reduced mass of electron and proton. Also, the total energy of the electron in the ground state of the hydrogen atom is -13.6 eV. For H-atom, reduced mass is m
e
whereas the positronium, the reduced mass is m = \(\frac{m_e}{2}\).
Hence, the total energy of the electron in the ground state of the positronium atom is
\(\frac{-13.6 \mathrm{eV}}{2}\) = -6.8eV.
Section D
[Case Study Based Questions]
Question 29.
Read the following paragraph and answer the questions that follow.
Consider a parallel plate capacitor of plate area A and plate separation d. If the space between the plate is vacuum, its capacitance is given by
C
0
= \(\frac{\varepsilon_0 A}{d}\) or E
0
= \(\frac{\sigma}{\varepsilon_0}\) = \(\frac{Q}{A \varepsilon_0}\)
The potential difference between the capacitor plates will be
V
0
= E
0
× d = \(\frac{Q d}{A \varepsilon_0}\)
Capacitance of the capacitor in the presence of dielectric medium of dielectric constant k in thickness t is given as
C = \(\frac{\varepsilon_0 A}{(d-t)+\frac{t}{k}}\)
(i) The capacity of a spherical conductor of radius R is [1]
(a) \(\frac{R}{4 \pi \varepsilon_0}\)
(b) \(\frac{4 \pi \varepsilon_0}{R}\)
(c) 4πε
0
R
(d) 4πε
0
R²
Answer:
(c) 4πε
0
R
Capacity of a spherical conductor C = 4πε 0 R
(ii) A parallel plate capacitor has a capacitance 50 pF in air and 110 pF, when immersed in an oil. The dielectric constant K of the coil [1]
(a) 0.45
(b) 0.55
(c) 1.10
(d) 2.20
Answer:
(d) 2.20
C = \(\frac{\varepsilon_0 A}{d}\)
50 μF = \(\frac{\varepsilon_0 A}{d}\)
When it is in oil, K need to be find out.
110 μF = K × 50 μF
K = \(\frac{110}{50}\) = 2.20
(iii) The parallel plate of area A are separated by two different dielectric as shown in figure. The net capacitance is [1]
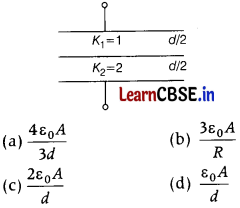
Answer:
(a) Kε
0
\(\frac{A}{d}\)
Parallel plate capacitor, C = Kε
0
\(\frac{A}{d}\)
Or
The potential of the two plates of capacitor are +10 V and -10 V. The charge on one of the plates is 40 C. The capacitance of the capacitor is [1]
(a) 2F
(b) 4F
(c) 0.5 F
(d) 0.25 F
Answer:
(a) 2F
The potential difference across the two parallel plate capacitor is10V – (-10V) = 20V
Capacitance = \(\frac{Q}{A}\) = \(\frac{40}{20}\) = 2 F
(iv) The capacity of parallel plate condenser depends on [1]
(a) the type of metal used
(b) the thickness of plates
(c) the potential applied across on the plate
(d) the separation between the plates
Answer:
(d) the separation between the plates
C = \(\\frac{\varepsilon_0 A}{d}\) = C = \(\frac{1}{d}\)
Therefore, the capacity of parallel plate condenser depends on the separation between the plates.
![]()
Question 30.
Read the following paragraph and answer the questions that follow.
L-C-R Series Circuit
A resistance R, an inductance L and capacitor C are connected in series to a source of alternating emf E is given by
E = E
0
sin ωt
Voltage across the resistance is V
R
= RI
Voltage across the inductor is V
L
= IX
L
Voltage across the capacitor is V
C
= X
C
I
Then, effective value of current
I
0
= \(\frac{E_0}{\sqrt{R^2+\left(X_L-X_C\right)^2}}\)
and impedance, Z = \(\sqrt{R^2+\left(X_L-X_C\right)^2}\)
= \(\sqrt{R^2+\left(ωL-\frac{1}{\omega C}\right)^2}\)
(i) With increase in frequency of an AC supply, the impedance of an LCR series circuit [1]
(a) remains constant
(b) increases
(c) decreases
(d) decreases at first, becomes minimum and then increases
Answer:
(d) decreases at first, becomes minimum and then increases
First decreases and then increases after reaching a minimum value.
(ii) In an LCR series circuit, the AC voltage across R, L and C comes out as 10 V, 10 V and 20 V, respectively. The voltage across the entire combination will be [1]
(a) 30 V
(b) 10√3V
(c) 20 V
(d) 10√2 V
Answer:
(d) 10√2 V
V = \(\sqrt{V_R^2+\left(V_L-V_C\right)^2}\) = 10√2 V
(iii) In LCR series circuit, connected to a source E, at resonance [1]
(a) the voltage across i?is zero
(b) the voltage across R is equal to the applied voltage
(c) the voltage across C is zero
(d) the voltage across C is equal to the applied voltage
Answer:
(b) the voltage across R is equal to the applied voltage
E = \(\sqrt{V_R^2+\left(V_L-V_C\right)^2}\)
At resonance, V
L
= V
C
⇒ E = V
R
i.e. Whole applied voltage appeared across the resistance.
(iv) The reactance of a coil when used in the domestic AC power supply (220 V, 50 cycles per second) is 50 Q. The inductance of the coil in nearly [1]
(a) 2.2 H
(b) 1.6 H
(c) 0.22 H
(d) 0.16 H
Answer:
(d) 0.16 H
X
L
= 2πfL
L = \(\frac{X_L}{2 \pi f}\) = \(\frac{50}{2 \pi \times 50}\) = 0.16 H
Or
In the case of an inductor, [1]
(a) voltage lags the current by nil
(b) voltage leads the current by π/2
(c) voltage leads the current by π/3
(d) voltage leads the current by π/4
Answer:
(b) voltage leads the current by nil
In case of an inductor, voltage leads the current by \(\frac{\pi}{2}\).
Section E
Question 31.
(i) Define the term conductivity of a metallic wire. Write its SI unit. [2]
(ii) Specific resistances of copper, silver and constantan are 1.78 × 10
-6
Ω-cm, 10
-6
Ω-cm and 48 x 10
-6
Ω-cm, respectively. Which is the best conductor and why? [2]
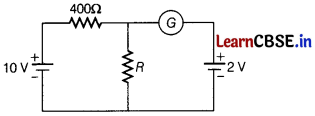
(iii) If the galvanometer G does not show any deflection, then what is the value of R? [1]
Answer:
(i) Conductivity: The reciprocal of resistivity of a conductor is known as conductivity. It is expressed as
σ = \(\frac{1}{ρ}\)
The SI unit of conductivity is mho per metre (Ω
-1
-V
-1
).
(ii) The best conductor is silver because electrical conductivity is inversely proportional to the resistivity and resistivity of silver is least.
(iii) The given situation is shown below.
Applying Kirchhoff’s voltage law in the loop ABCDE FA, we get
400l + 2 – 10 = 0
⇒l = \(\frac{8}{400}\) = \(\frac{1}{50}\) A
Applying kirchhoff’s voltage law in loop ABEFA, we get
400l + Rl – 10 = 0
⇒(400 + R) l = 10
⇒(400 + R) × \(\frac{1}{50}\) = 10
⇒400 + R = 500
⇒R = 100 Q
Or
(i) A conductor of length l is connected to a DC source of potential V. If the length of the conductor is tripled by gradually stretching it, keeping V constant, how will
(a) drift speed of electrons and
(b) resistance of the conductor be affected? Justify your answer. [4]
(ii) For wiring in the home, one uses Cu wires or Al wires. What considerations are involved in this? [1]
Answer:
(i) When a wire is stretched, then there is no change in the material of the wire, hence its volume remains constant.
The potential V = constant, l’ = 3l
(a)
v oc \(\frac{1}{l}\) [∵ other factors are constants]
So, when length is tripled, drift velocity gets one-third.
(b) ∵ Volume remains constant for conductor,
V
1
= V
2
A
1
l
1
= A
2
l
2
A
1
l = A
2
(3l)
[∵ length is tripled after stretching]
∴ A
2
= \(\frac{A_1}{3}\)
i.e. When length is tripled, area of cross-section is reduced to \(\frac{A}{3}\).
Hence, R = ρ \(\frac{l’}{A’}\) = ρ \(\frac{3l}{\frac{A}{3}}\) = 9ρ \(\frac{l}{A}\) = 9R
Thus, new resistance will be 9 times of its original value.
(ii) The Cu wires or Al wires are used for wiring in the home.The main considerations involved in this process are cost of metal and good conductivity of metal.
![]()
Question 32.
(i) What are the different ways by which emf can be induced in a conductor? [2]
(ii) Using Faraday’s law, derive the expression for motional emf induced in a straight conductor moving in a uniform magnetic field in a plane perpendicular to the direction of magnetic field. [2]
(iii) How can we find the polarity of induced emf ? [1]
Answer:
(i) Since, according to Faraday’s law, the emf induced in a conductor whenever magnetic flux through it changes is given by
ε = -N \(\frac{d \phi}{d t}\)
where, N = Number of turns of coil (conductor)
and ϕ = flux through the conductor
But ϕ = BA cos θ
where, B = magnetic field,
A = area of conductor
and θ = angle between B and A (Area vector).
ε = -N \(\frac{d}{d t}\)(BA cosθ)
Thus emf can be induced by
(a) changing the number of turns of coil, N
(b) change the intensity of magnetic field, B
(c) changing the area linked with field, A
(d) changing the orientation of coil, θ
(ii) Motional electromotive force and Faraday’s law: Consider a uniform magnetic field B confined to the region ABCD and a coil PQRS is placed inside the magnetic field. At any time t, the part P’Q = S’R = y of the coil is inside the magnetic field. Let l be the length of the arm of the coil.
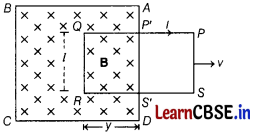
Area of the coil inside the magnetic field at time t,
∆S = QR × RS’ = ly
Magnetic flux linked with the coil at any timef,
ϕ = B∆S = Bly
The rate of change of magnetic flux linked with the coil is given by,
\(\frac{d \phi}{d t}\) = \(\frac{d}{d t}\) (Bly)
= BI \(\frac{d y}{d t}\) = BIv
where, v is the velocity with which the coil is pulled out of the magnetic field.
If e is the induced emf, then according to Faraday’s law, e = – \(\frac{d \phi}{d t}\) or e = -BIv
(iii) Polarity of induced emf can be given by Lenz’s law.
According to Lenz’s law, the polarity of induced emf is such that, it tends to produce a current which opposes the change in magnetic flux that produced it.
From the Fleming’s right hand rule, the induced current due to induced emf will flow from the end R to Q, i.e. along SRQP in the coil.
Or
For an AC voltage given by E = E
0
sin ωt applied to a circuit containing pure resistance R, derive an expression for
(i) instantaneous current. [2]
(ii) average power dissipated over one complete cycle of AC. [2]
(iii) Draw a phasor diagram representing phase relation between instantaneous current and voltage. [1]
Answer:
(i) AC through Resistor Suppose a resistor of resistance R is connected to an AC source of < emf with instantaneous value (E), which is given E = E
0
sin ωt …(i)
Let E be the potential drop across resistance (R).