Students must start practicing the questions from CBSE Sample Papers for Class 12 Physics with Solutions Set 7 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Physics Set 7 with Solutions
Time : 3 hrs
Max. Marks : 70
Instructions
1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary.
(i) c = 3 × 10
8
m/s
(ii) m
e
= 9.1 × 10
-31
kg
(iii) e = 1.6 × 10
-19
C
(iv) µ
0
= 4π × 10
-7
TmA× 10
-1
(v) h = 6.63 × 10
-34
Js
(vi) ε
0
= 8.854 × 10
-112
C
2
N
-1
m
-2
(vii) Avogadro’s number = 6.023 × 10
23
per gram mole
Section A
Question 1.
An AC voltage is applied to a resistance R and an inductor L in series. If R and the inductive reactance are both equal to 3 Q, the phase difference (in rad) between the applied voltage and the current in the circuit is
(a) \(\frac{\pi}{4}\)
(b) \(\frac{\pi}{2}\)
(c) zero
(d) \(\frac{\pi}{6}\)
Answer:
(a) \(\frac{\pi}{4}\)
By tan ϕ = \(\frac{\pi}{4}\) = \(\frac{\pi}{4}\) [∵ X
L
= ωL]
⇒ tan ϕ = \(\frac{\pi}{4}\) ⇒ tan ϕ = 1
⇒ ϕ = tan-1 (1)
⇒ ϕ = 45°
⇒ ϕ = \(\frac{\pi}{4}\)
Question 2.
A ray of light is incident at the glass-water interface at an angle (as shown below) and it emerges finally parallel to the surface of water, then the value of n
g
would be
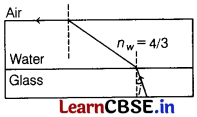
(a) (4/3) sin i
(b) 1/sin i
(c) 4/3
(d) 1
Answer:
(b) 1/sin i
The given ray of light is as shown below
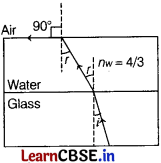
For glass-water interface, applying Snell’s law,
\(\frac{\sin i}{\sin r}\) = \(\frac{n_w}{n_g}\)
⇒ n
g
= \(\frac{n_w \sin r}{\sin i}\) ………(i)
For water-air interface, angle of incidence in water = r
Again, \(\frac{\sin r}{\sin 90^{\circ}}\) = \(\frac{n_a}{n_w}\) = \(\frac{1}{n_w}\)
⇒ sin r = \(\frac{1}{n_w}\) ……(ii)
From Eqs. (i) and (ii), we get
n
g
= \(\frac{\left(n_w\right) \times\left(\frac{1}{n_w}\right)}{\sin i}\) ⇒ n
g
= \(\frac{1}{\sin i}\)
![]()
Question 3.
If emf induced in a coil is 2 V by changing the current in it from 8 A to 6 A in 2 × 10
-3
s, then the coefficient of self-induction is [1]
(a) 2 × 10
-3
H
(b) 10
-3
H
(c) 05 × 10
-3
H
(d) 4 × 10
-3
H
Answer:
(a) 2 × 10
-3
H
Given, induced emf,e = 2 V,
i
1
= 8 A, i
2
= 6 A
and ∆t = 2 × 10
-3
s
.-. Coefficient of self-induction,
L = \(\frac{e}{\frac{\Delta i}{\Delta t}}\) = \(\frac{-2}{\frac{(6-8)}{2 \times 10^{-3}}}\)
= \(\frac{-2 \times 2 \times 10^{-3}}{-2}\)
= 2 × 10
-3
H
Question 4.
The electrical resistance of depletion layer is large because [1]
(a) it has no charge carriers
(b) it has a large number of charge carriers
(c) it contains electrons as charge carriers
(d) it has holes as charge carriers
Answer:
(a) it has no charge carriers
The depletion layer in a diode is depleted of charge carriers and contains only immobile ions. So, its resistance is large.
Question 5.
A long magnet of pole strength q
m
is cut into two parts such that the ratio of their lengths is 1 : 3. The ratio of pole strength of these pieces is [1]
(a) 1 : 3
(b) 3 : 1
(c) 1 : 6
(d) 1 : 1
Answer:
(d) 1 : 1
Pole strength of magnet is independent of its length and it always remains same for a given magnet, i.e. 1:1.
Question 6.
A given beam of α-particles has a distribution of impact parameter b, so that the beam is scattered in various direction as shown below
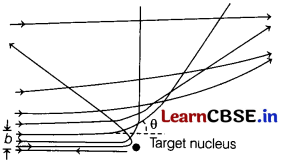
Then, [1]
(a) b = minimum at θ ≅ 0
(b) b = maximum at θ ≅ π
(c) b = minimum at θ ≅ π
(d) b = maximum at θ at all values of 0
Answer:
(c) b = minimum at θ ≅ π
It has been seen that, an α-particle close to the nucleus suffers large scattering angle.
In case of head-on collision, the impact parameter is minimum and the α-particle rebounds back (θ ≅ π).
For large impact parameter, the α-particle goes nearly undeviated or shows small deflection (θ ≅ 0).
Question 7.
The nuclear radius of a certain nucleus is 7.2 fm and it has charge of 1.28 × 10
-17
C. The number of neutrons inside the nucleus is [1]
(a) 136
(b) 142
(c) 140
(d) 132
Answer:
(a) 136
Nuclear radius, R = R
0
A
1/3

Question 8.
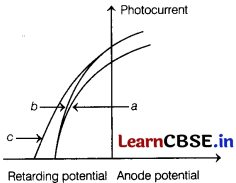
The figure shows a plot of photocurrent versus anode potential for a photosensitive surface for three different radiations. Which one of the following is a correct statement? [1]
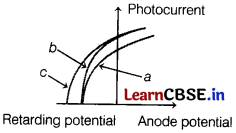
(a) Curves a and b represent incident radiations of different frequencies and different intensities.
(b) Curves a and b represent incident radiations of same frequency but of different intensities.
(c) Curves b and c represent incident radiations of different frequencies and different intensities.
(d) Curves b and c represent incident radiations of same frequency having same intensity.
Answer:
(b) Curves a and b represent incident radiations of same frequency but of different intensities.
Since, in the graph, retarding potential is same for surfaces a and b and photocurrent is different, so for curves, they have same frequency but different intensity of light.
![]()
Question 9.
The speed of electromagnetic wave in vacuum depends upon the source of radiation and [1]
(a) increases as we move from γ-rays to radio waves
(b) decreases as we move from γ-rays to radio waves
(c) is same for all of them
(d) None of the above
Answer:
(c) is same for all of them
Speed of electromagnetic waves in vacuum
= \(\frac{1}{\sqrt{\mu_0 \varepsilon_0}}\)
Therefore, speed of electromagnetic wave in vacuum is same for all of them.
Question 10.
A charged particle moves in a uniform magnetic field. The velocity of the particle at some instant makes an acute angle with the magnetic field. The path of the particle will be [1]
(a) a straight line
(b) a circle
(c) a helix with uniform pitch
(d) a helix with non-uniform pitch
Answer:
(c) a helix with uniform pitch
When particle enters a uniform magnetic field at an angle other than 0°, 90° or 180°, the path followed is helix with uniform pitch.
Question 11.
An electron is moving along positive X-axis. To get it moving on an anti-clockwise circular path in XY-plane, a magnetic field is applied [1]
(a) along positive F-axis
(b) along positive Z-axis
(c) along negative F-axis
(d) along negative Z-axis
Answer:
(b) along positive Z-axis
To move the electron in XY-plane, force on it must be acting in the y-direction initially. Thus, the magnetic field must be applied in positive Z-axis.
Question 12.
The particle nature of light is not confirmed by [1]
(a) photoelectric effect
(b) scattering of X-ray by electrons
(c) diffraction of electrons
(d) Compton effect
Answer:
(c) diffraction of electrons
The diffraction of electrons show wave nature of electrons.
For questions 13 to 16 two statements are given-one labelled
Assertion (A) and other labelled Reason (R).
Select the correct answer to these questions from the options as given below.
(a) If both A and R are true and R is the correct explanation of A.
(b) If both A and R are true but R is not the correct explanation of A.
(c) If A is true but R is false.
(d) If both A and R are false.
Question 13.
Assertion (A) Electric field lines of force never cross each other.
Reason (R) Electric field at a point super impose to give one resultant electric field. [1]
Answer:
(b) If both A and R are true but R is not the correct explanation of A.
Electric lines of force never cross each other because if electric lines of force cross each other, then the electric field at the point of intersection will have two direction simultaneously which is not possible.
Electric field is a vector quantity, so on adding electric field at a point on superimpose give one resultant electric field.
Question 14.
Assertion (A) The coulomb force is the dominating force in the universe.
Reason (R) The coulomb force is weaker than the gravitational force. [1]
Answer:
(d) If both A and R are false.
Gravitational force is the dominating force in nature and not coulomb’s force. The gravitational force is the weakest force. Also,
Coulomb’s force >> gravitational force.
Question 15.
Assertion (A) Current is a scalar quantity.
Reason (R) Electric current arises due to continuous flow of charged particles or ions. [1]
Answer:
(b) If both A and R are true but R is not the correct explanation of A.
Current is a scalar quantity, if current carrying wire is bent at some point, then also current in the wire remains the same, while a vector quantity always changes by changing its direction.
Question 16.
Assertion (A) At resonance, L-C-R series circuit have a zero current.
Reason (R) At resonance, in L-C-R series circuit the current and emf are 180° out of phase with each other. [1]
Answer:
(d) If both A and R are false.
In L-C-R series circuit at resonance,
X
L
= X
C
∴ Z = \(\sqrt{R^2+\left(X_L+X_C\right)^2}\) =R
i.e., Z
min
= R
∴ I
max
= \(\frac{V}{Z_{\min }}\) = \(\frac{V}{R}\)
and cos ϕ = \(\frac{R}{Z}\) = \(\frac{R}{R}\) = 1 = cos 0°
⇒ ϕ = 0
Section B
Question 17.
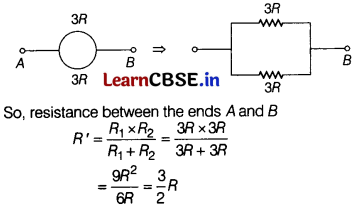
A wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter? [2]
Answer:
As shown in figure, the two resistances of value 3R each are in parallel with each other.
![]()
Question 18.
The focal length of objective and eye lens of a microscope are 4 cm and 8 cm respectively. If the least distance of distinct vision is 24 cm and object distance is 4.5 cm from objective lens, then what is the magnifying power of the microscope? [2]
Answer:
For objective lens,
\(\frac{1}{f_0}\) = \(\frac{1}{v_0}\) – \(\frac{1}{u_0}\)
\(\frac{1}{(+4)}\) = \(\frac{1}{v_0}\) – \(\frac{1}{(-4.5)}\)
⇒ v
0
= 36 cm
∴ |M
D
| = \(\frac{v_0}{u_0}\)(1 + \(\frac{D}{f_e}\))
= \(\frac{36}{4.5}\) (1 + \(\frac{24}{8}\))
= 32
Question 19.
Two identical photocathodes recieve light of frequencies f
1
and f
2
. If the velocities of the photoelectrons coming out are respectively v
1
and v
2
, what is the difference between square of their velocity? [2]
Answer:
Using, E = W
0
+ k
max
hf
1
= W
0
+ \(\frac{1}{2}\) mv
1
2
hf
2
= W
0
+ \(\frac{1}{2}\) mv
2
2
h(f
1
– f
2
) = \(\frac{1}{2}\) m(v
1
2
– v
2
2
)
(v
1
2
– v
2
2
) = \(\frac{2h}{m}\) (f
1
– f
2
)
Question 20.
Explain with the help of a circuit diagram, the working of a p-n junction diode as half-wave rectifier. [2]
Answer:
In this, the AC voltage to be rectified is connected to the primary coil of a step-down transformer and secondary coil is connected to the diode through resistor R
L
across which, output is obtained.
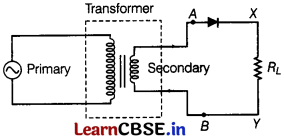
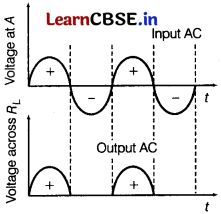
Working: During positive half-cycle of the input AC, the p-n junction is forward biased. Thus, the resistance in p-n junction becomes low and current flows. Hence, we get output in the load.
During negative half-cycle of the input AC, the p-n junction is reverse biased. Thus, the resistance of p-n junction is high and current does not flow. Hence, no output is in the load.
Question 21.
A lens is made of two different materials. A point object is placed on the principal axis of this lens. How many images will be obtained? [2]
Or
Show analytically from the lens equation that when the object is at the principal focus, the image is formed at infinity. [2]
Answer:
Since, refractive index of each material is different, so the lens will have two different focal lengths, one for each material. Hence, two images will formed.
Or
Given, u = -f
Lens equation,
\(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)
\(\frac{1}{v}\) + \(\frac{1}{f}\) = \(\frac{1}{f}\) = \(\frac{1}{v}\) = 0
Thus, v = \(\frac{1}{0}\) = infinity
Section C
Question 22.
Two identical parallel plate (air) capacitors C
1
and C
2
have capacitance C each. The space between their plates is now filled with dielectrics as shown in the figure. If the two capacitors still have equal capacitance, then obtain the relation between dielectric constants K, K
1
and K
2
. [3]
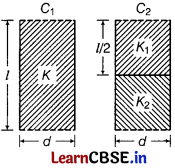
Answer:
After inserting the dielectric medium, let their capacitances become C’
1
and C’
1
.
For C
1
, C’
1
= KC …(i)
For C
2
, C’
2
= \(\frac{K_1 \varepsilon_0(A / 2)}{d}\) + \(\frac{K_2 \varepsilon_0(A / 2)}{d}\)
C’
2
acts as if two capacitors each of area A/2 and separation d are connected in parallel combination
C’
2
= \(\frac{\varepsilon_0 A}{d}\)(\(\frac{K_1}{2}\) + \(\frac{K_2}{2}\))
C’
2
= C (\(\frac{K_1+K_2}{2}\)) [∵ C = \(\frac{\varepsilon_0 A}{d}\)] …..(ii)
According to the problem, C’
1
= C’
2
⇒ KC = C (\(\frac{K_1+K_2}{2}\))
⇒ K = \(\frac{K_1+K_2}{2}\)
Question 23.
(i) Deduce the relation between current I flowing through a conductor and drift velocity v
d
of the electrons. [2]
(ii) Figure shows, a plot of current I flowing through the cross-section of a wire versus the time t. Use the plot to find the charge flowing in t
2
second through the wire. [1]
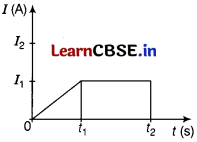
Answer:
Consider a conductor of length l and A be the uniform area of cross-section.
Volume of a conductor = Al
If the conductor contains free electrons n per unit volume.
Then, number of free electrons in the conductor = nAl
If e is the charge of an electron, then total charge on all free electrons in the conductor is given by
q = nAle …….(i)
Time taken by the free electrons to cross the length of the conductor
t = \(\frac{1}{v_d}\) …..(ii)
Since, current is the rate of flow of the charge through conductor.
I = \(\frac{q}{t}\)
Using Eqs. (i) and (ii), we get
I = \(\frac{q}{t}\)
⇒ I = neA v
d
……(iii)
(ii) Area under l-t curve on f-axis is charge flowing through the conductor.
Q = \(\frac{1}{2}\) × t
1
× l
1
+ (t
2
– t
1
) × l
1
![]()
Question 24.
Use Biot-Savart’s law to derive the Expression for the magnetic field on the axis of a current carrying circular loop of radius a. Draw the magnetic field lines due to a circular wire carrying current (I).
Answer:
Let us consider a circular loop of radius a with center 0 as shown below.
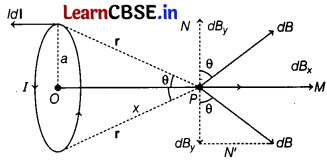
According to Biot-Savart’s law, magnetic field due to
a current element is given by dB = \(\frac{\mu_0}{4 \pi}\) \(\frac{I d \mathbf{l} \times \hat{\mathbf{r}}}{r^2} .\)
where, r = \(\sqrt{x^2+a^2}\)
∴ dB = \(\frac{\mu_0}{4 \pi}\) \(\frac{I dl \sin 90^{\circ}}{\left(x^2+a^2\right)}\) (∵ dl ⊥ r)
and direction of dB is perpendicular to the plane containing Idl and r.
Resolving dB along the X-axis and Y-axis,
dB
x
= dB sinθ and dB
y
= dB cosθ.
Now, by taking the contribution of whole current loop, we get
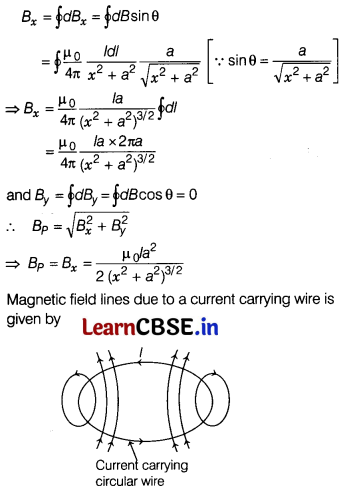
Question 25.
(i) Can the instantaneous power output of an AC source ever be negative? Can the average power output be negative? [2]
(ii) Establish an expression for the average voltage of AC voltage V = V
0
sin ωt over the time interval t =0 and t = π/ω. [1]
Answer:
(i) Yes, the instantaneous power can be negative
as P
instantaneous
= I
in
× V
in
= I
0
sin ωt × V
0
cos ωt
No, because it is average, so it will be positive.
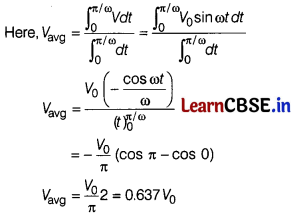
(ii) Average voltage, V
m
or V
av
= \(\frac{2 V_0}{\pi}\) = 0.637 V
0
Question 26.
(i) Name the electromagnetic waves used in LASIK eye surgery and why? [1]
(ii) Name the electromagnetic radiations used for (a) water purification and (b) eye surgery. [1]
(iii) Why does microwave oven heats up a food item containing water molecules most efficiently? [1]
Answer:
(i) LASIK eye surgery, ultraviolet rays are used because of their short wavelength they can be focused into very narrow beam.
(ii) (a) Ultraviolet radiation (b) Infrared radiation
(iii) Microwave oven heats up the food items containing water molecules most efficiently because the frequency of microwaves matches the resonant frequency of water molecules.
Question 27.
Using the relevant Bohr’s postulates, derive the expression for the
(i) radius of the nth orbit of the electron in H-atom. [1]
(ii) velocity of the electron in the nth orbit [2]
Answer:
(i) Electrostatic force of attraction, we have
\(\frac{m v^2}{r}\) = \(\frac{1}{4 \pi \varepsilon_0}\) × \(\frac{(Z e) e}{r^2}\)
mv² = \(\frac{Z e^2}{4 \pi \varepsilon_0 \times r}\) ………(i)
Second postulate, mvr = n × \(\frac{h}{2 \pi}\) ……(ii)
Then, from Eqs. (i) and (ii)
r = n² × \(\frac{h^2 \varepsilon_0}{\pi m Z e^2}\)
Acording to this equation, r
n
< n²
(ii) Velocity of electron in stationary orbit
By using, mvr = n × \(\frac{h}{2 \pi}\)
We have, v = n\(\frac{h}{2 \pi m r}\) then, v = \(\frac{Z e^2}{2 h \varepsilon_0}\) ⋅ \(\frac{1}{n}\)
Principal quantum number, n = 1,2, 3 1
V ∝ \(\frac{1}{n}\)
![]()
Question 28.
(i) Calculate the energy in fusion reaction
\({ }_{2}^{1} \mathrm{H}\) + \({ }_{2}^{1} \mathrm{H}\) → \({ }_{3}^{2} \mathrm{He}\) + n, where BE
of \({ }_{2}^{1} \mathrm{H}\) = 2.23 MeV and of \({ }_{3}^{2} \mathrm{He}\) = 7.73 MeV [1]
(ii) Determine the nuclear radii of
(a) \({ }_{27}^{60} \mathrm{Co}\)
(b) \({ }_{79}^{197} \mathrm{Au}\). [2]
Answer:
(i) According to the question,
\({ }_{2}^{1} \mathrm{H}\) + \({ }_{2}^{1} \mathrm{H}\) → \({ }_{3}^{2} \mathrm{He}\) +
0
n
1
∴ Energy of fusion = Binding energy of \({ }_{2}^{3} \mathrm{He}\)
– 2 × Binding energy of \({ }_{2}^{1} \mathrm{H}\)
= 7.73 – 2 × 2.23 = 3.27 MeV
(ii) Given,
A = 60
R
0
= 1.2 × 10
-15
m
As R = R
0
A
1/3
= 1.2 × 10
-15
× (60)
1/3
R = 4.7 × 10
-15
m
(b) A = 197
R
0
= 1.2 × 10
-15
m
As R = R
0
A
1/3
= 1.2 × 10
-15
× (197)
1/3
= 1.2 × 10
-15
× 5.818
= 6.98 × 10
-15
m
Or
(i) Write three characteristic properties of nuclear force. [1]
(ii) Draw a plot of potential energy of a pair of nucleons as a function of their separation. Write two important conclusions that can be drawn from the graph.
Answer:
(i) (a) It is attractive in nature but with a repulsive core. That is the reason that the nucleus is held together without collapsing on itself.
(b) Nuclear force is identical for all nucleons.
(c) The range of nuclear force is very short. All about 1 fermi, the nuclear force is much stornger than the repulsive coulomb’s force but at distance greater than 2.5 fermi, nuclear force is practically non-existent.
(ii)
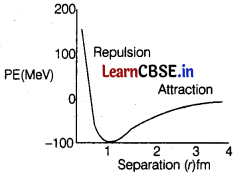
(a) The nuclear force is repulsive when the separation is less than 1fm.
(b) The nuclear force is attractive when the separation is greater than 1fm.
![]()
Section D
[Case Study Based Questions]
Question 29.
Read the following paragraph and answer the questions that follow.
When the diode is forward biased, it is found that beyond forward voltage, the conductivity is larger. At this instant, battery biasing for p-n junction, the potential barrier is overcome and the current increase rapidly with increase forward voltage. When reverse biased, voltage produces a very small current which almost remains constant with bias.
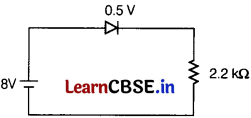
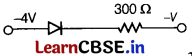
(i) In the circuit, if the forward voltage drop for the diode is 0.5 V, the current will be [1]
(a) 8.3 mA
(b) 3.4 mA
(c) 2.5 mA
(d) 3 mA
Answer:
(b) 3.4 mA
The voltage drop across resistance
= 8 – 0.5 = 7.5 V
Current, I = \(\frac{7.5}{2.2 \times 10^3}\) = 3.4 mA
(ii) In a full wave rectifier, input AC current has a frequency v. Then, find the output frequency. [1]
(a) \(\frac{v}{2}\)
(b) v
(c) 2v
(d) None of these
Answer:
(c) 2v
In a full wave rectifier, when input frequency is v, then output frequency is 2v.
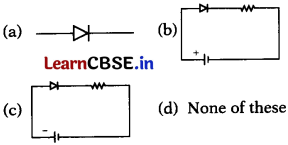
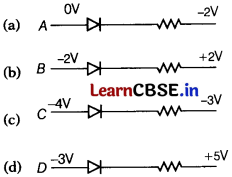
(iii) Which one is in forward bias? [1]
Answer:
In forward biasing p-side is connected with positive terminal and n-side with negative terminal of the battery.
(iv) The forward biased diode
Answer:
![]()
All others have cathode at higher potential than anode.
Or
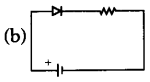
What is the current in the circuit shown below
(a) 0 A
(b) 10
-2
A
(c) 1 A
(d) 0.10 A
Answer:
(a) 0 A
The potential of p-side is move negative than that of n-side, hence diode is in reverse biased, hence no current flows.
![]()
Question 30.
Read, the following paragraph and answer the questions that follow
Interference of Light
Two sources are said to be coherent if they produce have of same frequency with a constant phase difference. Two independent sources of light cannot be coherent.Since, sound is a bulk property of matter, therefore two independent sources of sound can be identical in all respects and produce coherent wave. Division of wavefront and division of amplitude are two ways of coherent sources.
where, intensity of two wave
y
1
= a
1
cos(ωt + θ
1
)
y
2
= a
2
cos(ωt + θ
2
)
(i) The similarity between the sound waves and light waves is [1]
(a) both are electromagnetic waves
(b) both are longitudinal waves
(c) both have the same speed in a medium
(d) they can produce interference
Answer:
(d) they can produce interference
Sound waves and light waves both show interference.
(ii) Light travel through a glass plate of thickness t and refrective index n. If c is the velocity of light in vacuum, then time taken by light to travel the thickness of the plate will be [1]
(a) \(\frac{n t}{c}\)
(b) \(\frac{t}{n c}\)
(c) \(\frac{t c}{n}\)
(d) \(\frac{c}{n t}\)
Answer:
(a) \(\frac{n t}{c}\)
Time = \(\frac{t}{\left(\frac{c}{n}\right)}\) = \(\frac{n t}{c}\)
(iii) Intensities of the waves of light are I and 4I the maximum intensity of the resultant wave after superposition is [1]
(a) 5I
(b) 9I
(c) 16I
(d) 25I
Answer:
(b) 9I
I
max
= I
1
+ I
2
+ 2\(\sqrt{I_1 I_2}\)
So, I
max
=I + 4I + 2\(\sqrt{I.4I}\)
I
max
= 9I
Or
Two waves of intensity I undergo interference. The maximum intensity obtained is [1]
(a) \(\frac{I}{2}\)
(b) I
(c) 2I
(d) 4I
Answer:
(d) 4I
For maximum intensity, ϕ = 0
I = I
1
+ I
2
+ 2\(\sqrt{I_1 I_2}\) cosϕ
= I + I + 2\(\sqrt{I.I}\) cos 0° = 4I
(iv) The ratio of intensities of two waves are given by 4 : 1. The ratio of the amplitude of the two waves is [1]
(a) 2 : 1
(b) 1 : 2
(c) 4 : 1
(d) 1 : 4
Answer:
(a) 2 : 1
I a a² = \(\frac{a_1}{a_2}\) = \(\left(\frac{4}{1}\right)^{1 / 2}\) = \(\frac{2}{1}\)
Section E
Question 31.
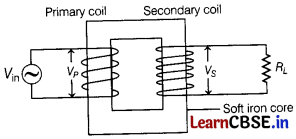
(i) A step-up transformer is shown below
(a) Explain its working principle. [1]
(b) Deduce the expression for the secondary to primary voltage in terms of the number of turns in the two coils. [1]
(c) In an ideal transformer, how is this ratio related to the currents in the two coils? [1]
(ii) How is the transformer used in large scale transmission and distribution of electrical energy over long distances?
Answer:
(i)
(a) Step-up transformer is a device which changes an alternating voltage of smaller value to a greater value. This is done using the principle of
The transformer consists of two sets of coils insulated from each other wound on a soft iron core.
Let N
P
be number of turns in the primary coil and N
S
be number of turns in the secondary coil, then for a step-up transformer, N
S
> N
P
.
Principle of Working:
When an alternating voltage is applied to the primary, the resulting current produces an alternating magnetic flux which links the secondary and induces an emf in it. The value of this emf depends on the number of turns in the secondary.
(b) Let ϕ be the flux in each turn in the core due to the current flowing in the primary coil. The value of induced emf in the secondary is given by
ε
S
= -N
S
\(\frac{d \phi}{d t}\)
This alternating flux ϕ also induces a back emf in the primary given by
ε
P
= -N
P
\(\frac{d \phi}{d t}\)
The voltage across the primary coil,
V
P
= ε
P
= -N
P
\(\frac{d \phi}{d t}\) …….(i)
The voltage across the secondary coil, when the switch is open,
V
S
= ε
S
= -N
S
\(\frac{d \phi}{d t}\) ………(ii)
From Eq. (i), \(\frac{d \phi}{d t}\) = \(-\frac{V_P}{N_P}\) ………(iii)
From Eq. (ii), \(\frac{d \phi}{d t}\) = \(-\frac{V_S}{N_S}\) ………(iv)
From Eqs. (iii) and (iv),
\(\frac{V_S}{N_S}\) = \(\frac{V_P}{N_P}\)
i.e., \(\frac{V_S}{V_P}\) = \(\frac{N_S}{N_P}\)
(c) For an ideal transformer, the resistance of primary and secondary coil are negligible, i.e. there are no energy losses.
Then, input power = output power i
P
V
P
= i
S
V
S
i.e. \(\frac{i_S}{i_P}\) = \(\frac{V_P}{V_S}\) = \(\frac{N_P}{N_S}\)
(ii) The transformers are used in large scale transmission and distribution of electrical energy over long distances. The output voltages of the AC generators at power stations are stepped up using step-up transformers. This reduces the current and hence i²R or resistive power losses in the transmitting electric wires is reduced. At the sub-stations near the consumers, this voltage is stepped down by step down transformers.
Then, at distributing sub-stations, the voltage is again stepped down to 240 V and supplied to us.
![]()
Or
(i) Define power for alternating current.
Derive an expression for the average power of a series L-C-R circuit connected to an AC source. [2]
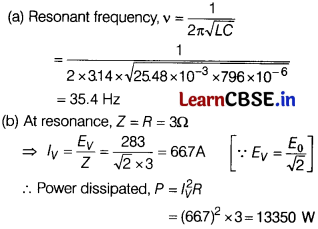
(ii) A sinusoidal voltage of peak value 283 V and frequency 50 Hz is applied to a series L-C-R circuit in which R = 3 Ω, L = 25.48 mH and C = 796 μF.
(a) What is the frequency of the source at which resonance occurs?
(b) Calculate the impedance, the current and power dissipated of resonant condition.
Answer:
(i) Power is defined as the rate of doing work. dW
P = \(\frac{d W}{d t}\) ………(i)
Or
Power is defined as the product of voltage and current.
In AC circuit, both emf and current change continuously with respect to time. So in it we have to calculate average power in complete cycle (0 → T).
Instantaneous power, P = EI ……(ii)
[∵ E = E0 sin ωt, I = /0 sin(ωt + ϕ)] Here, E and I are instantaneous voltage and current, respectively. If the instantaneous power remains constant for a small time dt, then small amount of work done in maintaining the current for a small time dt is
\(\frac{d W}{d t}\) = EI
dW = EI dt ………..(iii)
Integrating Eq. (iii) on both sides, we get
\(\int d W\) = \(\int_0^T E I d t\)
Total work done or energy spent in maintaining current over one full cycle,

(ii)
Question 32.
Two tiny spheres carrying charges 1.5 μC and 2.5 μC are located 30 cm apart. Find the potential and electric field
(i) at mid-point of the line joining the two charges. [2]
(ii) at a point 10 cm from this mid-point in a plane normal to the line and passing through the mid-point.
Hence, calculate the angle (α) subtended by the resultant intensity of electric field in case (ii). [3]
Answer:
Given, q
1
=1.5 μC = 1.5 × 10
-6
C,
q
2
= 2.5 μC = 2.5 × 10
-6
C
Distance between the two spheres = 30 cm = 0.3 m
(i) For the mid-point O, r
1
= r
2
= \(\frac{0.30}{2}\) = 0.15 m
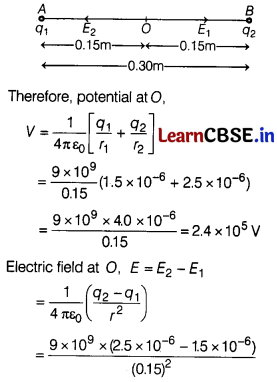
= 4.0 × 10
5
Vm
(ii) Consider point P in a plane normal to the line passing through the mid-point, where OP = 10 cm = 0.1 m.


Or
Four charges are arranged at the comers of a square ABCD of side d as shown in the figure.
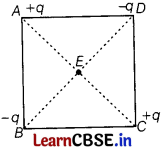
(i) Find the work required to put together this arrangement. [2]
(ii) A charge q0 is brought to the centre E of the square, the four charges being held fixed at its comers. How much extra work is needed to do this? [1]
(iii) Compute the work done by the charges in rearranging this arrangement to another similar square arrangement of the charges such that the side of the square now becomes 2d. [2]
Answer:
(i) Work done in making the system = – (Total electrostatic potential energy of the system)
We have, AB = BC =CD = DA = d
and AC = BD = \(\sqrt{d^2 + d^2}\) = \(\sqrt{2}\)d
There will be six pairs (four sides and two diagonals)

(ii) Extra work needed to bring charge q
0
to centre E
W = q
0
× electrostatic potential at E due to four charges
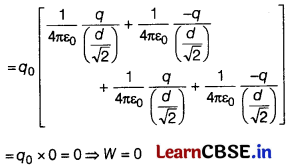
Hence, no work is required to bring any charge to centre E.
(iii) Initial electrostatic potential energy of the square arrangement of charges U
i
= U [from Eq. (i)]
∴ Electrostatic potential energy of new arrangement of charges,
U
f
= \(\frac{-q^2}{4 \pi \varepsilon_0(2 d)}\) [4 – \(\sqrt{2}\)] J = \(\frac{U}{2}\)
∴ Required work done for rearrangement of charges,
∆W = U
f
– U
i
= \(-\frac{U}{2}\) = \(\frac{q^2}{8 \pi \varepsilon_0 d}\) [4 – \(\sqrt{2}\)] J
![]()
Question 33.
State and derive mirror formula for a concave mirror. State the sign convention used. [5]
Answer:
Object AB is at a distance u from the pole, A
1
B
1
, is formed at a distance v from the mirror.
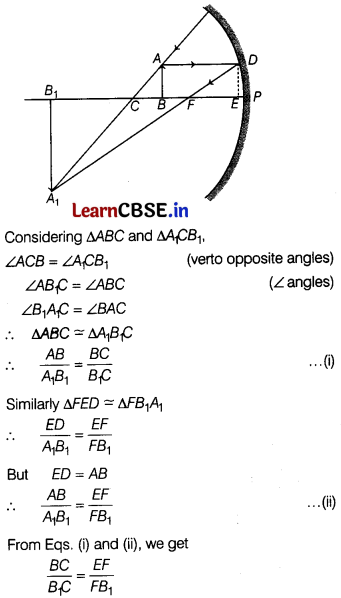

Sign convertion for ray diagrams
(i) All distances are measured from the pole of the mirror.
(ii) Distances measured in the direction of the incident rays are positive and vice-versa.
(iii) Distances measured above the principal axis are positive and vice-versa.
Or
Use the mirror equation to deduce that,
(i) an object placed between f and 2f of a concave mirror produces a real image beyond 2f.
(ii) a convex mirror always produces a virtual image independent of the location of the object.
(iii) the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
(iv) an object placed between the pole and focus of a concave mirror produces a virtual and enlarged image. [5]
Answer:
(i) For a concave mirror, the focal length is negative, along with object distance
According to mirror formula,
\(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\)
\(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{u}\) ……..(i)
Form questions,
2f < u < f \(\frac{1}{2f}\) > \(\frac{1}{u}\) > \(\frac{1}{u}\)
\(-\frac{1}{2f}\) < \(\frac{-1}{u}\) < \(\frac{-1}{f}\)
\(\frac{1}{f}\) – \(\frac{1}{2f}\) < \(\frac{1}{f}\) – \(\frac{1}{u}\) …….(ii)
Using Eqs. (i) and (ii), we get
\(\frac{1}{2f}\) < \(\frac{1}{v}\) < 0, v is negative 2f > v
Thus, image lies beyond 2f.
(ii) For convex mirror focal length is positive, object distance is negative From mirror formula,
\(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\)
\(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{v}\)
Using equation (ii), we get
\(\frac{1}{v}\) < 0 ⇒ v > 0
Thus, image is formed on the backside of the mirror. Convex mirrors always produce virtual images.
(iii) For a convex mirror, the focal length as is positive, object distance is negative.
From mirror formula,
\(\frac{1}{v}\) + \(\frac{1}{u}\) = \(\frac{1}{f}\)
⇒ \(\frac{1}{v}\) = \(\frac{1}{f}\) – \(\frac{1}{u}\)
if u < 0
∴ \(\frac{1}{v}\) > \(\frac{1}{f}\)
∴ v < f
Hence, image formed is diminished and located between focus and pole.