Students must start practicing the questions from CBSE Sample Papers for Class 12 Physics with Solutions Set 4 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Physics Set 4 with Solutions
Time : 3 hrs
Max. Marks : 70
Instructions
1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary.
(i) c = 3 × 10
8
m/s
(ii) m
e
= 9.1 × 10
-31
kg
(iii) e = 1.6 × 10
-19
C
(iv) µ
0
= 4π × 10
-7
TmA× 10
-1
(v) h = 6.63 × 10
-34
Js
(vi) ε
0
= 8.854 × 10
-112
C
2
N
-1
m
-2
(vii) Avogadro’s number = 6.023 × 10
23
per gram mole
Section A
Question 1.
In Rutherford’s nuclear model of the atom, if F
e
indicates electrostatic force between electron and nucleus and F
c
indicates the centripetal force on revolving electron, then [1]
(a) F
e
= F
c
(b) F
e
> F
c
(c) F
e
< F
c
(d) F
e
= oo and F
c
= 0
Answer:
(a).The electrostatic force of attraction (F
e
) between the revolving electrons and the nucleus provides the requisite centripetal force F
c
to keep them in their orbits.
Thus, for a dynamically stable orbit in a hydrogen atom,
F
e
= F
c
Question 2.
The electric potential as a function of distance x is as shown in figure.
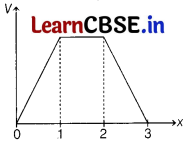
Which of the following graph correctly represents the variation of electric field intensity E as a function of x? [1]
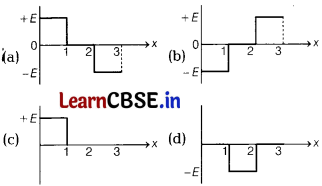
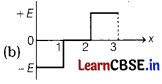
Answer:
As we know, electric field, E = \(-\frac{d V}{d x}\)
= negative slope of V-x graph
For x = 0 to x = 1, \(\frac{d V}{d x}\) = positive ⇒ E = negative
For x = 1 to x = 2, \(\frac{d V}{d x}\) = 0 ⇒ E = 0
For x = 2 to x = 3, \(\frac{d V}{d x}\) = negative ⇒ E = positive
So, variations of E as a function of x are correctly represented in option (b).
Question 3.
The current flowing through an inductor of self-inductance L is continuously increasing. The graph depicting the variation of magnetic potential energy stored with the current is [1]
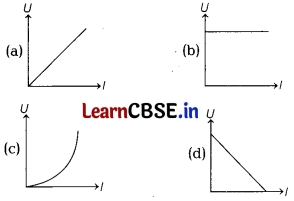
Answer:

Magnetic potential energy stored in an inductor is given as
U = \(\frac{1}{2}\) LI
2
=> U ∝ l
2
So, the correct graph is depicted in option (c).
![]()
Question 4.
In accordance with the Bohr’s model, find the quantum number that characterises the earth’s revolution around the sun in an orbit of radius 1.5 × 10
11
m with orbital speed 3 × 10
4
ms
-1
.
(Take, mass of earth = 6.0 × 10
24
kg) [1]
(a) 2.6 × 10
74
(b) 8.5 × 10
80
(c) 4.34 × 10
100
(d) 3.2 × 10
8
Answer:
(a) 2.6 × 10
74
Given, radius of orbit, r = 1.5 × 10
11
m,
Orbital speed, v = 3× 10
4
ms
-1
and mass of earth,
m = 6.0 × 10
24
kg
Angular momentum, L = mvr = \(\frac{nh}{2 \pi}\)

Question 5.
Two equal and opposite charges each of 2 C are placed at a distance of 0.04 m. Dipole moment of the system will be [1]
(a) 6 × 10
-8
C-m
(b) 8 × 10
-2
C-m
(c) 15 × 10
-2
C-m
(d) 8 × 10
-6
C-m
Answer:
(b) 8× 10
-2
C-m
Electric dipole moment, p = q × d
= 2 × 0.04 = 0.08 C-m
= 8 × 10
-2
C-m
Question 6.
There is a thin conducting wire carrying current. What is the value of magnetic field induction at any point on the conductor itself? [1]
(a) 1
(b) – 1
(c) zero
(d) Either (a) or (b)
Answer:
(c) zero
|d B| = \(\frac{\mu_0}{4 \pi}\left|\frac{/\left(d \mathbf{l} \times \mathbf{r}^{\prime}\right)}{r^3}\right|\) = \(\frac{\mu_0}{4 \pi} \times \frac{\mid d / \sin \theta}{r^2}\)
If point lies on the conductor, then θ = 0° or 180°. So, sin θ = 0, thus dB = 0.
Hence, the magnetic field induction at any point on the conductor itself is zero.
Question 7.
In a uniform magnetic field, an electron enters perpendicular to the field. The path of electron will be [1]
(a) ellipse
(b) circular
(c) parabolic
(d) linear
Answer:
(b) circular
When the charged particle enters in the magnetic field perpendicular to it, then the force on it due to magnetic field,
F = qvB sin 90° = qvB
The direction of this force is always perpendicular to motion of charged particle. The charged particle is moving under the influence of constant force but its direction is continuously changing. So, the particle will move in a circular path with constant velocity v.
Question 8.
Which of the following statement(s) is/are correct about an inductive circuit? [1]
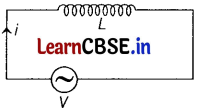
(a) In an inductive circuit, using Kirchhpff s loop rule, we get V – L \(\frac{di}{dt}\) = 0 , where the second term is the mutual induced emf in the inductor.
(b) The quantity ω is analogous to the conductance.
(c) The current phasor I is \(\frac{\pi}{2}\) ahead of the voltage phasor V.
(d) The average power supplied to an inductor over one complete cycle is zero.
Answer:
(d) The average power supplied to an inductor over one complete cycle is zero.
V – L \(\frac{di}{dt}\) = 0
In an inductive circuit, using Kirchhoff’s loop rule, we get where, the second term is the self-induced emf in the inductor and L is the self-inductance of the inductor.
The quantity ωL is analogous to the resistance and is called inductive reactance denoted by X
L
(= ωL). The current phasor I lags \(\frac{\pi}{2}\) behind the voltage phasor V, i.e. ϕ = \(\frac{\pi}{2}\).
When AC flows through an inductor, it generates the voltage and current as given by V = V
m
sin ωt and i
m
sin(ωt – \(\frac{\pi}{2}\)), respectively.
∴ Average power supplied to an inductor over one complete cycle,
P
av
= V
rms
× I
rms
× cos ϕ
= V
rms
× I
rms
× cos \(\frac{\pi}{2}\) = 0
So, statement given in option (d) is correct and rest are incorrect.
Question 9.
Voltage and current in an alternating circuit are given by
V = 5 sin(100πt – \(\frac{\pi}{6}\))
and I = 4 sin(100πt + \(\frac{\pi}{6}\)) [1]
(a) voltage leads the current by 30°
(b) current leads the voltage by 30°
(c) current leads the voltage by 60°
(d) voltage leads the current by 60°
Answer:
(c) urrent leads the voltage by 60°
Phase difference, ∆ϕ = ϕ
2
– ϕ
1
= \(\frac{\pi}{6}\) – (\(-\frac{\pi}{6}\)) = \(\frac{\pi}{3}\)
So, current leads the voltage by 60°.
![]()
Question 10.
A perfectly diamagnetic sphere has a small spherical cavity at its centre, which is filled with a paramagnetic substance. The whole system is placed in a uniform magnetic field B, then the field inside the paramagnetic substance is [1]

(a) zero
(b) B
(c) much greater than B but in opposite direction
(d) much greater than B and in same direction
Answer:
(a) zero
A perfectly diamagnetic substance opposes the field, so the field inside the paramagnetic substance is zero.
Question 11.
The de-Broglie wavelength of a particle is λ. What will be the wavelength of the particle, if its kinetic energy is \(\frac{K}{9}\)? [1]
(a) λ
(b) 2λ
(c) 3λ
(d) 4λ.
Answer:
(c) 3λ
de-Broglie wavelength, λ = \(\frac{h}{\sqrt{2 m K}}\)
When the KE is \(\frac{K}{9}\), then
λ’ = \(\frac{h}{\sqrt{2 m\left(\frac{K}{9}\right)}}\) = \(\frac{3 h}{\sqrt{2 m K}}\) = 3λ
Question 12.
A convex lens is immersed in a liquid of refractive index same as that of lens. In liquid, convex lens will behave like a [1]
(a) converging lens
(b) diverging lens
(c) plane glass
(d) None of these
Answer:
(c) plane glass
If f
i
be the focal length of lens in liquid, then
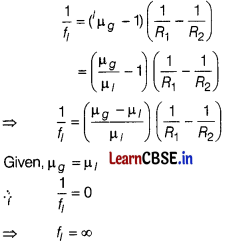
Thus, in liquid, convex lens will behave like a plane glass.
For questions 13 to 16 two statements are given-one labelled
Assertion (A) and other labelled Reason (R).
Select the correct answer to these questions from the options as given below.
(a) If both A and R are true and R is the correct explanation of A.
(b) If both A and R are true but R is not the correct explanation of A.
(c) If A is true but R is false.
(d) If both A and R are false.
Question 13.
Assertion (A) An electron on p-side of a p-n junction moves to n-side just an instant after diffusion of charge carriers across junction.
Reason (R) Drifting of charge carriers reduces the concentration gradient across junction. [1]
Answer:
(c) If A is true but R is false.
In a p-n junction, due to diffusion of electrons, a positive space charge region on n-side of the junction and a negative space charge region on p-side of the junction is formed which are called immobile ions.
Due to this, an electric field directed from positive charge towards negative charge develops. (Electric field is from n-side to p-side). Due to this field, an electron on p-side of the junction moves to n-side and a hole on n-side of the junction moves to p-side. This motion of charge carriers due to the electric field is called drift. Thus, a drift current, which is opposite in direction to the diffusion current, starts flowing. However,concentration gradient is due to doping of impurities. It is not affected by drift of charge carriers.
Therefore, A is true but R is false.
Question 14.
Assertion (A) Photoelectric effect demonstrates the wave nature of light. Reason (R) The number of photoelectrons is proportional to the frequency of light. [1]
Answer:
(d) If both A and R are false.
Photoelectric effect demonstrates the particle nature of light. Number of emitted photoelectrons depends upon the intensity of light.
Question 15.
Assertion (A) Changing magnetic flux can produce induced emf.
Reason (R) Faraday established induced emf experimentally. [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
Induced emf produce due to changing in magnetic flux, ε = \(-\frac{d \phi_B}{d t}\)
Question 16.
Assertion (A) The goggle have zero power.
Reason (R) Radius of curvature of both sides of lens of goggle is same. [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
\(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
For goggle, R
1
= R
2
∴ \(\frac{1}{f}\) = 0
P = \(\frac{1}{f}\) = 0
![]()
Section B
Question 17.
Draw the energy band diagrams of conductors and insulators. [2]
Solution:
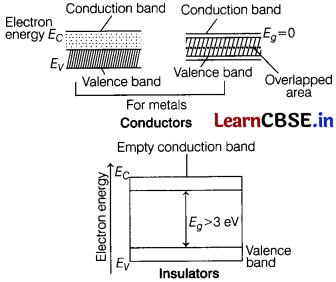
Question 18.
(i) With reference to photoelectric effect, define threshold wavelength. [1]
(ii) If the energy of a photon corresponding to a wavelength of 6000 Å is 3.32 × 10
-19
J, then
Calculate the photon energy for a wavelength of 4000 Å.
Answer:
(i) It is the maximum wavelength of incident light on the photosensitive material above which no photoemission of photoelectrons takes piace.
It is given as λ
0
= \(\frac{h c}{\phi_0}\)
where, ϕ
0
is work function.

Question 19.
Derive the expression for the resistivity of a good conductor in terms of the relaxation time of electrons. [2]
Answer:
Specific resistance or resistivity of the material of a conductor is defined as the resistance of a unit length with unit area of cross-section of the material of the conductor.
∴ R = ρ × \(\frac{l}{A}\) ⇒ ρ = \(\frac{R A}{l}\)
Substituting the value of R = \(\frac{m l}{n e^2 A \tau}\) in Eq (i)
Resistivity of the material, ρ = \(\frac{m}{n e^2 \tau}\)
Question 20.
Mention any two situations in which Snell’s law of refraction fails. [2]
Answer:Snell’s law of refraction fails in two situations
(i) When HR (total internal reflection) takes place at angle greater than the critical angle.
(ii) When light is incident normally on a surface as i = 0, r = 0.
Question 21.
When monochromatic light travels from a rarer to a denser medium, explain the following giving reasons.
(i) Is the frequency of reflected and refracted light same as the frequency of incident light? [1]
(ii) Does the decrease in speed imply a reduction in the energy carried by light wave. [1]
Or
(i) Show analytically from the lens equation that when the object is at the principal focus, the image is formed at infinity. [1]
(ii) A magician during a show makes a glass lens n = 1.47 disappear in a trough of liquid. What is the refractive index of the liquid? Could be liquid water? [1]
Answer:
(i) The frequency of reflected and refracted light remains same as that of incident light because frequency only depends on the source of light.
(ii) Since, the frequency remains same, hence there is no reduction in energy.
Or
(i) Given, u =-f
Lens equation is \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{f}\)
⇒ \(\frac{1}{v}\) + \(\frac{1}{f}\) = \(\frac{1}{f}\) ⇒ \(\frac{1}{v}\) = 0
v = \(\frac{1}{0}\) = infinity
(ii) If pi μ
1
= μ
2
, then f = ∞
Hence, the lens in the liquid acts like a plane sheet when refractive index of the lens and the surrounding is the same. Therefore,
μ
1
= μ
2
= 1.47
Thus, the liquid medium is not water.
It could be glycerine.
![]()
Section C
Question 22.
The potential difference across terminal of a cell were measured (in volt) against different current (in ampere) flowing through the cell. A graph was drawn which was a straight line ABC as shown below [3]
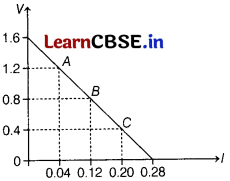
Determine from the graph
(i) Emf of the cell
(ii) Maximum current obtained from the cell and
(iii) internal resistance of the cell.
Answer:
(i) The emf of cell is the potential difference for zero current.
From the graph, the potential difference, V = 1.6 V.
∴ emf of cell, ε = 1.6 V
(ii) Maximum current is obtained from the cell when the terminal potential difference of the cell is zero,
i.e. l
max
= 0.28 A
(iii) Internal resistance of cell, r = \(\frac{ε}{l_max}\) = \(\frac{1.6}{0.28}\) = 5.71 Ω
Question 23.
(i) State Gauss’s law for electrostatic. [1]
(ii) Prove Gauss’s law for spherically symmetric surface. [2]
Answer:
(i) The surface integral of the electric field intensity over any closed surface (called Gaussian surface) in free space is equal to \(\frac{1}{\varepsilon_0}\) times the net charge enclosed within the surface.
ϕ
E
= \(\oint \mathbf{E} \cdot d \mathbf{S}\) = \(\frac{1}{\varepsilon_0}\)\(\sum_{i=1}^n q_i\) = \(\frac{q}{\varepsilon_0}\)
where, q = \(\sum_{i=1}^n q_i\), is the algebraic sum of all the charges inside the closed surface.
(ii) Electric flux through a surface element dS is given by
dϕ
E
= E . dS = \(\frac{1}{4 \pi \varepsilon_0}\) ⋅ \(\frac{q}{r^2}\)\(\hat{\mathbf{r}} \cdot(d S \hat{\mathbf{n}})\)
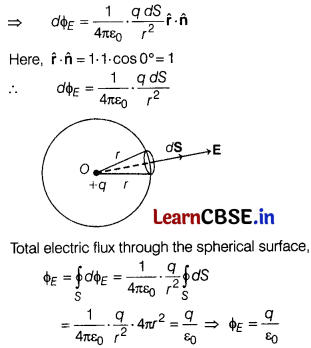
If there is no net charge within the closed surface, i.e. when q = 0, then ϕ
E
= 0.
The total electric flux through a closed surface is zero, if no charge is enclosed by the surface.
Question 24.
A long straight solid metal wire of radius R carries a current I uniformly distributed over its circular cross-section. Find the magnetic field at a distance r from the axis of wire (i) inside (ii) outside the wire. [3]
Answer:
(i) Let the point P be lying inside the wire at a perpendicular distance r from the axis of the wire. Consider a circular path of radius r around the axis of the wire. By symmetry, the magnetic field produced due to current flowing in the wire at any point over this path is tangential to it and equal in magnitude at all points on this path.
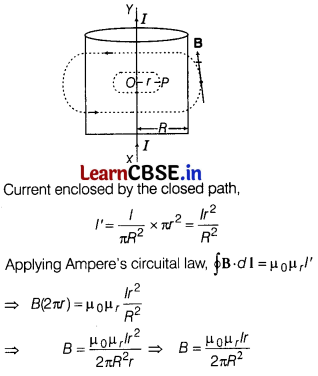
(ii) When point P is outside the wire, r >R, so that the current enclosed by closed path = l
Using Ampere’s circuital law, \(\oint \mathbf{B} \cdot d \mathbf{l}\) = μ
0
l
B × 2πr = μ
0
l or B = \(\frac{\mu_0 l}{2 \pi r}\)
![]()
Question 25.
Answer the following questions.
(i) Name the electromagnetic waves which are used for the treatment of certain forms of cancer. Write their frequency range. [1]
(ii) Thin ozone layer on top of stratosphere is crucial for human survival. Why? [1]
(iii) Why is the amount of the momentum transferred by the electromagnetic waves incident on the surface so small? [1]
Answer:
γ-rays. Its frequency range is from
3 × 10
19
Hz to 3 × 10
23
Hz.
(ii) The thin ozone layer on top of stratosphere absorbs most of the harmful ultraviolet rays coming from the sun towards the earth. They include UVA, UVB and UVC radiations which can destroy the life system on the earth. Hence, this layer is crucial for human survival.
(iii) Momentum transferred = Energy/Speed of light
= \(\frac{E}{C}\) = \(\frac{hv}{C}\) ≈ 10
2-22
Thus, the amount of the momentum transferred by the electromagnetic waves incident on the surface is very small.
Question 26.
(i) State Bohr’s quantisation condition for defining stationary orbits. How does de-Broglie’s hypothesis explain the stationary orbits? [2]
(ii) Find the relation between the three wavelengths λ
1
, λ
2
and λ
3
from the energy level diagram shown below. [1]
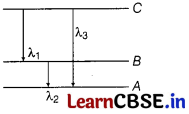
Answer:
(i) According to Bohr’s principle, electrons revolve in a stationary orbit of which energy and momentum are fixed. The momentum of
electrons in the fixed orbit is given by \(\frac{nh}{2\pi}\) (where, n = number of orbits).
According to de-Broglie’s hypothesis, the electron is associated with wave character. Hence, a circular orbit can be taken to be a stationary energy state only if it contains an integral number of de-Broglie wavelengths, i.e.
2πr = nλ
(ii) According to the question,

Question 27.
(i) Find the binding energy per nucleon
20
C
40
nucleus. Given,
m(
20
C
40
) = 39.962589 u,
m
n
= 1.008665 u and m
p
= 1.007825 u
Take, 1 amu = 931 MeV/C² [1]
(ii) The mass of a nucleus is less than the sum of the masses of constituent neutrons and protons. Comment. [2]
Answer:
(i) Number of protons = 20
Number of neutrons = 40 – 20 = 20
Total mass of 20 protons and 20 neutrons
= 20 m
p
+ 20 m
n
= 20 (m
p
+ m
n
)
= 20 (1.007825 + 1.008665)
= 40.3298 u
Mass defect, ∆m= 40.3298 – 39.962589
= 0.367211 × 931
= 341.873441 MeV
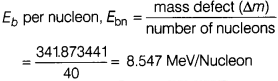
(ii) During the formation of a nucleus, energy is required to bind together the nucleons in a small space of order 10 -15 m. This energy is taken at the cost of the mass of the nucleons. Thus, the mass of nucleus formed is always less than the sum of masses of its constituents.
![]()
Question 28.
(i) Define self-inductance. Write its SI units. [1]
(ii) Derive the expression for self-inductance of a long solenoid of length l, cross- sectional area A having N number of turns. [2]
Or
The current through two inductors of self-inductance 12 mH and 30 mH is increasing with time at the same rate. 6raw graphs showing the variation of the
(i) emf induced with the rate of change of current in each inductor.
(ii) energy stored in each inductor with the current flowing through it.
Compare the energy stored in the coils, if the power dissipated in the coils is the same. [3]
Answer:
(i) Self-Inductance: It is the property of a coil by virtue of which, the coil opposes any change in the strength of current flowing through it by inducing an emf in itself. This induced emf is called back emf. When the current in a coil is switched ON the opposes the growth of the current and when the current is switched OFF, the self-induction opposes the decay of the current. So, self-induction is also called the inertia of electricity SI unit of self-inductance is henry.
(ii) Self-Inductance of Long Solenoid: A long solenoid is one whose length is very large as compared to its area of cross-section. The magnetic field B at any point inside such a solenoid is practically constant and is given by
B = \(\frac{\mu_0 N i}{l}\) = μ
0
ni [n = \(\frac{N}{l}\)]
where, μ
0
= magnetic permeability of free space,
N = total number of turns in the solenoid,
l = length of the solenoid
and n = number of turns per unit length.
∴ Magnetic flux through each turn of the solenoid,
ϕ = B × area of the each turn
ϕ = (μ
0
\(\frac{N}{l}\)i) A
where, A = area of each turn of the solenoid. Total magnetic flux linked with the solenoid
= Flux through each turn x Total number of turns
Nϕ = μ
0
\(\frac{N}{l}\)i A × N …(ii)
If L is coefficient of self-inductance of the solenoid, then
Nϕ = Li
From Eqs. (ii) and (iii), we get
Li = μ
0
\(\frac{N}{l}\)i A × N or L = \(\frac{\mu_0 N^2 A}{1}\)
If core of any other magnetic material n is placed, then
μ = μ
0
μ
r
[μ
r
= relative magnetic permeability]
∴ L = \(\frac{\mu_0 \mu_r N^2 A}{l}\)
Or
Given, L
1
= 12 mH, L
2
= 30 mH
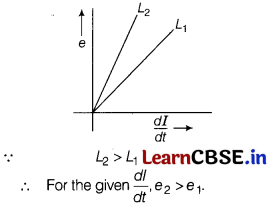
(i) Induced emf in the inductors, |e| = L\(\frac{dl}{dt}\)
As, \(\frac{dl_1}{dt}\) = \(\frac{dl_2}{dt}\) ⇒ e ∝ L
Thus, graph of e versus \(\frac{dl}{dt}\) for two inductors is as shown in the figure.
(ii) Energy stored in inductor, U = \(\frac{1}{2}\)Li
For a given L, U a l²
Also, \(\frac{dl_1}{dt}\) = \(\frac{dl_2}{dt}\)
Thus, U versus I graph is curved as shown in the figure.

Section D
[Case Study Based Questions]
Question 29.
Read size following paragraph and answer the questions that follow Refraction involves change in the path of light due to change in the medium.
When a beam of light encounters another transparent medium, a part of light gets reflected back into the first medium, while the rest enters the other. The direction of propagation of an obliquely incident ray of light, that enters the other medium, changes at the interface of two – media . The phenomenon is called refraction of light.
(i) Which quantity remains unchanged after refraction? [1]
(a) Wavelength
(b) Frequency
(c) Intensity
(d) Amplitude
Answer:
(b) Frequency
Refraction does not change the frequency of light.
(ii) A ray of light strikes an air-glass interface at an angle of incidence i and get refracted at an angle of refraction r. Then, on increasing the value of i, the value of r will [1]
(a) also increase
(b) also decrease
(c) remain unchanged
(d) None of the above
Answer:
(a) also increase
From Snell’s law of refraction,
a
µ
g
= \(\frac{sin i}{sin r}\) = constant
Since, angle of incidence increases, so the angle of refraction will increase, so that the ratio (\(\frac{sin i}{sin r}\)) is constant.
(iii) For the same angle of incidence, the angles of refraction in media P, Q and R the are 35°, 25° and 15°, respectively.
If vP, vQ and vR are velocity of light in medium P, Q and R, then [1]
(a) v
P
= v
Q
= v
R
(b) v
P
> v
Q
> v
R
(c) v
P
= v
Q
> v
R
(d) v
P
= v
Q
< v
R
Answer:
(b) v
P
> v
Q
> v
R
According to Snell’s law,
µ = \(\frac{sin i}{sin r}\) or µ ∝ \(\frac{1}{sin r}\)
µ is maximum for R, since r is minimum.
Also, µ = \(\frac{C}{v}\) v = \(\frac{C}{µ}\)
Therefore, if µ is maximum, v is minimum, i.e. velocity of light is minimum in medium R and order of velocity will be v
P
> v
Q
> v
R
.
Or
The image formed by an objective of a compound microscope is [1]
(a) virtual and diminished
(b) real and diminished
(c) real and enlarged
(d) virtual and enlarged
Answer:
Objective of a compound microscope is a convex lens. Thus, it forms real and enlarged image when an object is placed between its focus and lens.
(iv) Velocity of light in glass is 2 x 108 m/s and that in air is 3 x 108 m/s. By how much would an ink dot appear to be raised when covered by a glass plate 6 cm thick? [1]
(a) 2 cm
(b) 4 cm
(c) 8 cm
(d) 2.6 cm
Answer:
(a) 2 cm
Given, velocity of light in glass,
v = 2 × 10
8
m/s
Velocity of light in air, c = 3 × 10
8
m/s
∴ Refractive index of glass with respect to air,
a
µ
g
= \(\frac{c}{v}\) = \(=\frac{3 \times 10^8}{2 \times 10^8}\) = 1.5
∴ Normal shift in the position of ink dot,
d = t(1 – \(\frac{1}{{ }^a \mu_g}\)) = 6(1 – \(\frac{1}{1.5}\)) [∵ t = 6 cm]
\(\frac{1}{2}\) = 2 cm
Question 30.
Read the following paragraph and answer the questions that follow.
Bohr’s Atomic Model According to Bohr’s atomic model and concept of electronic configuration in an isolated atom, the electrons have certain definite discreate amount of energy corresponding to different shell and subshells, i.e. there are well-defined energy level of electron in an isolated atom.
But in a crystal due to interatomic interaction, valence electrons are shared by more than one atom. The energy band which includes the energy levels of valence electron is called valence band.
The energy band which includes the energy levels of conduction energy is called conduction band.
(i) Which one is not a compound of semiconductor? [1]
(a) CdS
(b) GaAs
(c) CdSe
(d) B
Answer:
(d) B
Compound of semiconductor are CdS, GaAs and CdSe but Boron (B) is not compound of semiconductor.
(ii) The resistivity and conductivity of semiconductor is [1]
(a) ρ ~10
-5
-10
6
Ωm, σ ~10
5
-10
6
sm
-1
(b) ρ ~10
-6
-10
5
Ωm, σ ~10
-5
-10
+6
sm
-1
(c) ρ ~10
-8
-10
-6
Ωm, σ ~10
6
-10
-8
sm
-1
(d) ρ ~10
-10
-10
-8
Ωm, σ ~10
+10
-10
+8
sm
-1
Answer:
(a) ρ ~10
-5
-10
6
Ωm, σ ~10
5
-10
6
sm
-1
The resistivity of semiconductor is
ρ ~10
-5
-10
6
Ωm
The conductivity of semiconductor is
σ ~10
5
-10
6
sm
-1
(iii) The minimum energy required for shifting electrons from valence band to conduction band is called [1]
(a) energy band
(b) conduction electrons
(c) forbidden gap
(d) None of the above
Answer:
(a) energy band
The minimum energy required for shifting electron from valence band to conduction band is called energy band.
![]()
(iv) The electron and hole concentration in a semiconductor are related as [1]
(a) n
e
n
h
= n
i
2
(b) n
e
n
h
≠ n
i
2
(c) n
e
= n
h
(d) n
e
≠ n
h
Answer:
(a) n
e
n
h
= n
i
2
The relation between electron and hole concentration in a semiconductor is
n
e
n
h
= n
i
2
Or
The energy gaps of C, Si and Ge are [1]
(a) 5.4 eV, 1.1 eV, 0.7 eV
(b) 5.6 eV, 1.6 eV, 0.9 eV
(c) 6.2 eV, 1.3 eV, 0.6 eV
(d) 7.2 eV, 2.4 eV, 9.2 eV
Answer:
(a) 5.4 eV, 1.1 eV, 0.7 eV
The energy gap of C, Si and Ge are 5.4 eV, 1.1 eV and 0.7 eV respectively.
Section E
Question 31.
(i) (a) An AC voltage V = V
m
sin ωt is applied across an inductor of inductance L. Find the instantaneous power P
i
supplied to the inductor. [1]
(b) Draw the plot showing the variation of the Pt with ωt of the AC source used. [1]
(c) Also, define wattless current of the circuit. [1]
(ii) Calculate the impedance of the given AC circuit. [1]
(iii) An ideal inductor is in turn put across 220 y 50Hz and 220V, 100Hz supplies. Will the current flowing through it in the two cases be the same or different? [1]
Answer:
(i) (a) In an inductor, the current lags the voltage by 90°. If the source voltage is sinusoidal, then the current is also sinusoidal, but shifted in phase. The instantaneous power defined as the product of the instantaneous voltage and current can also be seen to be sinusoidal in time. However, in contrast to the resistive load, the instantaneous power in the inductor goes negative for part of the cycle of the source driving it.
As, V(t) = V
m
sin ωt
l(t) = – l
m
cos ωt
Instantaneous power,

(b) The variation of with cot is as given in the figure
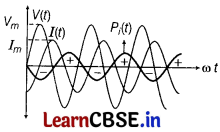
The instantaneous power alternates positive and negative at twice the frequency of source supplying it.
(c) The current which consumes no power for its maintenance in the circuit is called wattless current.
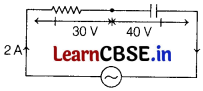
(ii) In the given circuit, l = 2 A
V
C
= 40 V = IX
C
⇒ 40 = 2 × X
C
⇒ X
C
= 20 Ω
V
R
= 30V = IR
⇒ 30 = 2 × R ⇒ R = 15 Ω
Impedance, Z = \(\sqrt{R^2+X_C^2}\) = \(\sqrt{15^2+20^2}\) = 25 Ω
(iii) The current flowing through the inductor will be more in first case because inductive reactance (X L = 2πfl) is less than that in second case.
Or
(i) (a) State the principle of working of a transformer. [1]
(b) Can a transformer be used to step-up or step-down a DC voltage? [1]
(ii) (a) Mention the reasons for energy losses in an actual transformer. [1]
(b) Specify the two characteristic properties of the material suitable for making core of a transformer. [1]
(iii) The power transmission lines need input power at 2300 V to a step-down transformer with its primary windings having 4000 turns. What should be the number of turns in the secondary windings in order to get output power at 230 V? [1J
Answer:
(i) (a) A transformer is based on the principle of mutual induction, i.e. whenever the amount of magnetic flux linked with the coil changes, an emf is induced in the neighbouring coil. This changing flux sets up an induced emf in the secondary coil, also self induced emf in primary coil.
(b) No, transformer cannot be used to step-up or step-down a DC voltage.
(ii) (a) Reasons for energy losses in actual
transformer
I. Joule heating Energy is lost in resistors of primary and secondary winding due to generation of heat (I2Fit).
II. Flux leakage Energy is lost due to coupling of primary and secondary coils not being perfect, i.e. whole of magnetic flux generated in primary coil is not linked with the secondary coil.
III. Eddy currents The alternating magnetic flux induces eddy currents in the iron core and causes heating.
IV. Hysteresis loss This is the loss of energy due to repeated magnetisation and demagnetisation because of AC in it.
(b) Two characteristic properties of the material suitable for making core of a transformer are
I. Low hysteresis loss or high permeability
II. and high susceptibility
(iii) Given, V
P
= 2300 V, N
P
= 4000 turns and V
S
= 230 V
We know that, V
S
/ V
P
= N
S
/ N
P
N
S
= \(\frac{V_S}{V_P}\) × N
S
= \(\frac{230}{2300}\) × 4000
= 400 turns
Question 32.
(i) (a) What is the focal length of a lens combination as shown below? [1]
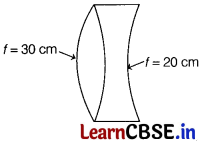
(b) Is the system a converging or a diverging lens? Ignore thickness of the lenses. [1]
(ii) At what angle should a ray of light be incident on the face of a prism of refracting angle 60°, so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is 1.524. [3]
Answer:
(i) (a) Given, focal length of convex lens, f
1
= 30 cm
Focal length of concave lens, f
2
= -20 cm
Using the formula of combination of lenses,
\(\frac{1}{f}\) = \(\frac{1}{f_1}\) + \(\frac{1}{f_2}\) = \(\frac{1}{30}\) – \(\frac{1}{20}\)
= \(\frac{2-3}{60}\) = \(-\frac{1}{60}\) ⇒ f = -60 cm
(b) Since, the focal length of combination is negative in nature. So, the combination behaves like a diverging lens, i.e. as a concave lens.
(ii) Given, angle of prism, A = 60°
Refractive index of prism, μ = 1.524
Let i be the angle of incidence. The angle of incidence at the other surface is equal to the critical angle i
c
because it just suffers total internal refraction.
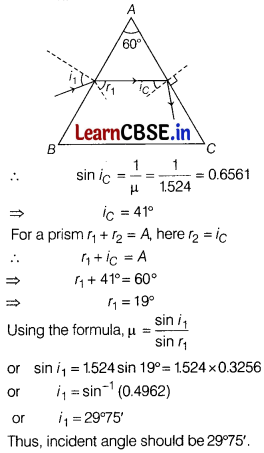
Or
(i) Define the power of lens. [2]
(ii) An angular magnification (magnifying power) of 24 is desired using an objective of focal length 1.25 cm and an eyepiece of focal length 5 cm. How will you set up the compound microscope? [3]
Answer:
(i) Power of lens It is the ability to diverge or converge the light rays incident on it. It is defined as the reciprocal of focal length.
P = \(\frac{1}{f(in m)}\) = \(\frac{100}{f(in cm)}\)
(ii) We assume the microscope in common usage, i.e. the final image is formed at the least distance of distinct vision,
D =25 cm, f
e
= 5 cm
∴ Angular magnification of the eyepiece,
m
e
= 1 + \(\frac{D}{f_e}\) = 1 + \(\frac{25}{5}\) = 6
As total magnification, m = m
e
× m
0
∴ Angular magnification of the objective,
m
0
= \(\frac{m}{m_e}\) = \(\frac{24}{6}\) = 4
As real image is formed by the objective, therefore

Question 33.
(i) Derive the expression for the capacitance of a parallel plate capacitor having plate area A and plate separation d. [3]
(ii) Two parallel plate capacitors of capacitances C
1
and C
2
such that C
1
= 2 C
2
are connected across a battery of V volt as shown in the figure. Initially, the key (K) is kept closed to fully charge the capacitors. The key is now thrown open and a dielectric slab of dielectric constant K is inserted in the two capacitors to completely fill the gap between the plates. Find the ratio of
(a) the net capacitance and
(b) the energies stored in the combination before and after the introduction of the dielectric slab. [2]
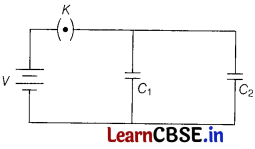
Answer:
(i) Parallel plate capacitor consists of two thin conducting plates each of area A held parallel to each other at a suitable distance d. One of the plates is insulated and other is earthed. And also there is vacuum between the plates.
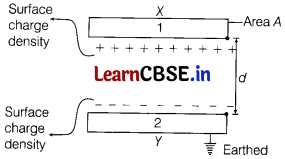
Suppose the surface density of charge on each plate is a We know that, the intensity of electric field at a point between two plane, parallel sheets of equal and opposite charges is σ/ε
0
, where s0 is the permittivity of free space.
The intensity of electric field between the plates will be given by E = \(\frac{\sigma}{\varepsilon_0}\)
The charge on each plate is q and the area of each plate is A. Thus,
σ = \(\frac{q}{A}\) and so, E = \(\frac{q}{\varepsilon_0 A}\) ……(i)
Now, let the potential difference between the two plates be V volt. Then, the electric field between the plates is given by
E = \(\frac{V}{d}\) or V = Ed
Substituting the value of £ from Eq. (i), we get
V = \(\frac{qd}{\varepsilon_0 A}\)
Capacitance of the parallel plate capacitor is given by
C = \(\frac{q}{V}\) = \(\frac{q}{q d / \varepsilon_0 A}\) or C = \(\frac{\varepsilon_0 A}{d}\)
(ii) (a) Given, C
1
= 2C
2
…(i)
Net capacitance after filling the gap with dielectric slab is given by

(b) Energy stored in the combination before introducing the dielectric slab,
U
initial
= \(\frac{1}{2}\)\(\frac{Q^2}{3 C_2}\)
Energy stored in the combination after introducing the dielectric slab,
U
final
= \(\frac{1}{2}\)\(\frac{Q^2}{3K C_2}\)
Ratio of energies stored
\(\frac{U_{\text {initial }}}{U_{\text {final }}}\) = \(\frac{K}{1}\)
Or
(i) Derive an expression for the potential energy of an electric dipole placed in a uniform electric field. [3]
(ii) Discuss the conditions of stable and unstable equilibrium for above case. [2]
Answer:
(i) Let at any instant, dipole makes an angle θ with the direction of electric field E. Two equal and opposite forces +qE and -qE act on the two point charges of dipole.
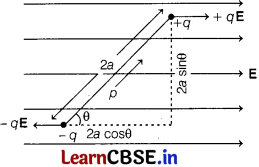
These forces form a couple whose torque (τ) is given by
τ = F × perpendicular distances between forces
⇒ τ = qE × (2a sin θ)
= [q (2a) ] E sin θ
⇒ τ = pE sin θ
where, p = g(2a) is electric dipole moment.
If the dipole is rotated through a small angle dθ against the torque, then small work done is given
by dW = x dθ
⇒ dW = (pE sinθ)dθ
The total work done in rotating the dipole from angle θ
1
, to θ
2
with the direction of electric field E is given by
W = \(\int d W\) = \(\int_{\theta_1}^{\theta_2} p E \sin \theta d \theta\)
= pE \([-\cos \theta]_{\theta_1}^{\theta_2}\)
= pE [cosθ
1
– cosθ
2
]
This work done is stored in the form of electrostatic potential energy.
Electrostatic potential energy,
U = pE [cos θ
1
– cos θ
2
]
If θ
1
= 90° and θ
2
= θ, then
U = pE (cos 90° – cos θ)
= – pE cos θ
= -p . E [∵ cos 90°=0]
This is the required expression of potential energy of an electric dipole placed in a uniform electric field.
(ii) For stable equilibrium
When θ = 0°,
Minimum potential energy, U
min
= -pE cos θ
= -pE cos 0°
⇒ U
min
= -pE
The potential energy of an electric dipole is minimum and dipole attains stable equilibrium.
For unstable equilibrium
When θ = 180°,
Potential energy, U = – pE cos θ = -pE cos 180°
= -pE(-1) = pE
Thus, the potential energy is maximum and in this situation dipole is said to be in unstable equilibrium.
Thus, when dipole is parallel to electric field, then it is said to be in stable equilibrium and when dipole is anti-parallel to electric field, then it is referred as in unstable equilibrium.