Students must start practicing the questions from CBSE Sample Papers for Class 10 Physics with Solutions Set 3 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Physics Set 3 with Solutions
Time : 3 hrs
Max. Marks : 70
Instructions
1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary.
(1) c = 3 × 10
8
m/s
(ii) m
e
= 9.1 × 10
-31
kg
(iii) e = 1.6 × 10
-19
C
(iv) µ
0
= 4π × 10
-7
TmA× 10
-1
(v) h = 6.63 × 10
-34
Js
(vi) ε
0
= 8.854 × 10
-112
C
2
N
-1
m
-2
(vii) Avogadro’s number = 6.023 × 10
23
per gram mole
Section A
Question 1.
An object of mass 1 kg contains 4 × 10
20
atoms. If one electron is removed from every atom of the solid, the charge gained by the solid of 1 g is [1]
(a) 2.8 C
(b) 6.4 × 10
-2
C
(c) 3.6 × 10
-3
C
(d) 9.2 × 10
-4
C
Solution:
(b) 6.4 × 10
-2
C
Here, number of electrons removed in 1 g
= number of atoms in 1 g
or n = \(\frac{4×10^2}{10^3}\)
.-.Charge, q = ne = 4 × 10
17
× 1.6 × 10
-19
= 6.4 × 10
-2
C
Question 2.
An electron of charge (e) is moving parallel to uniform magnetic field B with constant velocity v. The force acting on electron is [1]
(a) Bev
(b) \(\frac{1}{2}\)
(c) \(\frac{1}{2}\)
(d) zero
Solution:
(d) zero
The force on electron, F = qvB sin θ.
The electron is moving parallel to the magnetic field,
so θ = 0°
∴ F = qvB sin 0° = 0
Question 3.
The instantaneous magnetic flux linked with a coil is given by
ϕ = (5t³ – 100f + 300)Wb
The emf induced in the coil at time t = 2 s is [1]
(a) -40 V
(b) 40 V
(c) 140V
(d) 300V
Solution:
(b) 40 V
Given,
ϕ = (5t³ – 100f + 300)Wb, t = 2 s
Induced electromotive force,
e = \(-\frac{d \phi}{d t}\) = \(-\frac{d}{d t}\left(5 t^3-100 t+300\right)\)
⇒ e = -5 × 3t³ + 100 = -5 × 3(2)² + 100
= -5 × 12 + 100 = -60 + 100 = 40 V
![]()
Question 4.
If the orbital radius of the electron in a hydrogen atom is 4.7 × 10
11
m. Compute the kinetic energy of the electron in hydrogen atom. [1]
(a) 15.3 eV
(b)-15.3eV
(c) 13.6 eV
(d) – 13.6 eV
Solution:
(a) 15.3 eV
Kinetic energy of an electron is given by

Question 5.
Two parallel plates of area A are separated by two different dielectrics as shown in figure. The net capacitance is [1]
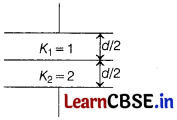
(a) \(\frac{4 \varepsilon_0 A}{3 d}\)
(b) \(\frac{3 \varepsilon_0 A}{R}\)
(c) \(\frac{2 \varepsilon_0 A}{d}\)
(d) \(\frac{\varepsilon_0 A}{d}\)
Solution:
(a) \(\frac{4 \varepsilon_0 A}{3 d}\)
We know that, capacitance of parallel plate capacitor,
C = \(\frac{K \varepsilon_0 A}{d}\)
As given in figure, two capacitors are connected in series, hence net capacitance C’ is given as
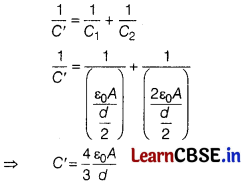
Question 6.
In an experiment on photoelectric effect, with the increase in potential difference of emitter and collector plate, keeping the frequency and intensity fixed of the incident light, the photoelectric current [1]
(a) increases
(b) decreases
(c) remains constant
(d) increases initially and then becomes constant
Solution:
(d) increases initially and then becomes constant
Keeping the frequency of the light and its intensity fixed, firstly with the increase in the positive potential of collector plate, the photoelectric current increases. At some stage, for a certain positive potential of collector plate, the photoelectric current becomes maximum or saturates. If we further increase the potential of collector plate, the photocurrent does not increase.
Question 7.
A current carrying circular loop of radius R is placed in the XT-plane with centre at the origin. Half of the loop with x > 0 is now bent, so that it now lies in the FZ-plane. Which of the following statement is correct about the later situation? [1]
(a) The magnitude of magnetic moment now decreases.
(b) The magnetic moment does not change.
(c) The magnitude of B at (0,0, z), z >>R ‘ increases.
(d) The magnitude of B at (0,0, z), z >> R unchanged.
Solution:
(a) The magnitude of magnetic moment now decreases.
The magnetic moment, M = l × πR².
Initially, it acts perpendicular to the loop along z-direction. When half of the current loop is bent in YZ-plane, then magnetic moment due to half current loop in XY-plane, M
1
= l(πR²/2) acting along z-direction.
And magnetic moment due to half current loop in VZ-plane, M
2
= l(πR²/2) acting along x-direction.
Net magnetic moments,
M
net
= \(\sqrt{M_1^2+M_2^2}\)
= \(\sqrt{\left(1 \pi R^2 / 2\right)^2+\left(l \pi R^2 / 2\right)^2}\)
= \(\frac{1 \pi R^2}{2} \sqrt{2}<M\)
i.e. Magnitude of magnetic moment now decreases.
Question 8.
A 220 V AC supply is connected between points A and B (figure). What will be the potential difference across the capacitor? [1]
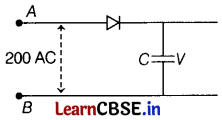
(a) 220 V
(b) 110 V
(c) 0 V
(d) 220√2 V
Solution:
(d) 220√2 V
As p-n junction conducts during positive half cycle only, so the diode connected here will work in positive half cycle.
Potential difference across C = Peak voltage of the given AC voltage
V
0
= V
Kms
√2 = 220√2 V.
![]()
Question 9.
Following figures show the arrangement of bar magnets in different configurations. Each magnet has magnets in different configurations and has magnetic dipole moment m. Which configuration has highest net magnetic dipole moment? [1]

(a) Only I
(b) Only II
(c) Both I and II
(d) None of the above
Solution:
(a) Only I
Here, magnetic moment for each configuration is given as
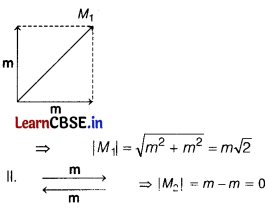
Therefore, configuration I has higher net magnetic dipole moment.
Question 10.
The amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is B
0
= 510 nT. What is the amplitude of the electric field part of the wave? [1]
(a) 130 NC
-1
(b) 153 NC
-1
(c) 170 NC
-1
(d) 190 NC
-1
Solution:
(b) 153 NC
-1
Given, amplitude of magnetic field part of harmonic electromagnetic wave, B
0
= 510 nT
Speed of light in vacuum, c = \(\frac{E_0}{B_0}\)
where, E
0
is the amplitude of electric part of the wave.
=> 3 × 10
8
= \(\frac{E_0}{510 \times 10^{-9}}\)
or E
0
= 153 NC
-1
Thus, the amplitude of the electric field part of wave is 153 NC
-1
.
Question 11.
In the a-particle scattering experiment, the shape of the trajectory of the scattered a-particles depend upon [1]
(a) Only on impact parameter
(b) Only on the source of a-particle
(c) Both impact parameter and source of a-particle
(d) impact parameter and the screen material of the detector.
Solution:
(a) Only on impact parameter
In a-particle scattering experiment, the shape of the trajectory depends on the impact parameter only.
Question 12.
If a medium of relative permeability p had been present instead of air, the mutual inductance would be [1]
(a) \(M=μ_rμ_0 n_1 n_2π r_1 l\)
(b) \(M=μ_0 n_1 n_2π r_1^2 l\)
(c) \(M=μ_r n_1 n_2π_1^2 l\)
(d) \(M=μ_rμ_0 n_1 n_2π r_1^2 l\)
Solution:
(d) \(M=μ_rμ_0 n_1 n_2π r_1^2 l\)
Air as the medium within the solenoids.
Instead, if a medium of relative permeability μ
r
had been present, the mutual inductance would be \(M=μ_rμ_0 n_1 n_2π r_1^2 l\).
It is also important to know that the mutual inductance of a pair of coils, solenoids etc., depends on their separation as well as their relative orientation.
For questions 13 to 16 two statements are given-one labelled
Assertion (A) and other labelled Reason (R).
Select the correct answer to these questions from the options as given below.
(a) If both A and R are true and R is the correct explanation of A.
(b) If both A and R are true but R is not the correct explanation of A.
(c) If A is true but R is false.
(d) If both A and R are false.
Question 13.
Assertion (A) The photoelectrons produced by a monochromatic light beam incident ‘on a metal surface have different value of kinetic energy.
Reason (R) The work function of the metal is its characteristics property. [1]
Solution:
(b) If both A and R are true but R is not the correct explanation of A.
The kinetic energy of emitted photoelectrons varies from zero to a maximum value. Work function depends on metal used.
![]()
Question 14.
Assertion (A) Lenz’s law does not violate the principle of conservation of energy.
Reason (R) Induced emf always opposes the change in magnetic flux responsible for its production. [1]
Solution:
(a) If both A and R are true and R is the correct explanation of A.
Lenz’s law (that the direction of induced emf is always such as to oppose the change that cause it) is • direct consequence of the law of conservation of energy.
Question 15.
Assertion (A) The conductivity of an intrinsic semiconductor depends on its temperature.
Reason (R) The conductivity of an intrinsic semiconductor is slightly higher than that of a lightly doped p-type semiconductor. [1]
Solution:
(c) If A is true but R is false.
The conductivity of an intrinsic semiconductor is less than that of a lightly doped p-type semiconductor. Also, with the increase in the temperature, conductivity of intrinsic semiconductor increase.
Therefore, A is true but R is false.
Question 16.
Assertion (A) The refractive index of diamond is √6 and that of liquid is √3. If the light travels from diamond to the liquid, it will totally reflected when the angle of incidence is 45°.
Reason (R) n = \(\frac{1}{sin i_c}\) where n is the refractive index of diamond with respect to liquid and i
c
is the critical angle. [1]
Solution:
(a) If both A and R are true and R is the correct explanation of A.
Refractive index of diamond with respect to liquid,

This means that, when the ray of light while travelling from diamond to liquid is incident at an angle of 45°, then it will be totally reflected due to TIR. Therefore, both A and R are true and R is the correct explanation of A.
Section B
Question 17.
Draw and explain the output waveform across the load resistor R, is the input waveform is as shown below [2]
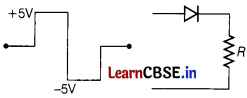
Solution:
When the input voltage of +5V is applied across diode, it get forward biased and hence a output of +5V is obtained across R, while when the input voltage of -5V is applied across the diode, it gets reversed biased. So, no output is obtained across R.
The output waveform is

Question 18.
Threshold frequency of metal is f
0
. When light of frequency 2f
0
is incident on metal plate, maximum velocity of electron emitted is v
1
. When frequency of incident radiation is increased to 5f
0
, maximum velocity of electrons emitted is v
2
. Find the ratio of v
1
to v
2
. [2]
Solution:
According to Einstein’s photoelectric equation,

Question 19.
An equiconvex lens of focal length f is cut into two equal halves in thickness. What is the focal length of each half? [2]
Solution:
Focal length can be given as
\(\frac{1}{f}=(\mu-1)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\)
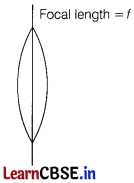
Where μ is the refractive index of the lens medium and R
1
&R
2
are radii of curvature.
Equiconvex lens have the same radius of curvature

Hence, focal length of each half becomes twice of the original value.
Question 20.
The resistivity of pure silicon is 3000 Ω-m and the electron and hole mobilities are 0.12 m
2
V
-1
s
-1
and 0.045 m
2
V
-1
S
-1
respectively, determine
(i) the resistivity of a specimen of the material when 10
19
atoms of phosphorous are added per m
3
. [1]
(ii) the resistivity of the specimen, if further 2 × 10
19
boron atoms per m
3
are also added. [1]
Solution:
(i) When 10
19
donor atoms of phosphorous are added per m
3

Question 21.
Show that for near normal viewing from rarer to denser medium, refractive index of the denser medium
r
μ
d
can be expressed as
r
μ
d
= \(\frac{\text { Real depth of object }}{\text { Apparent depth of object }}\) [2]
Or
Using Huygens’ principle, when an oblique wavefront is incident on the reflecting surface making an angle of incidence i with the surface, show that it gets reflected making the same angle. [2]
Solution:
A ray of light incident normally on XY, along OA passes straight along OAA’ (as shown in figure below).
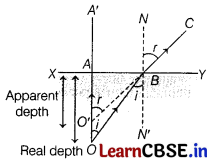
Another ray of light from 0 incident at ∠i on surface XY along OB deviates away from normal. It is refracted at ∠r along BC. On producing backwards B’C meets OA at O’. Therefore, O’ is virtual image of O.
Apparent depth = AO’
Real depth = OA
Now, ∠BOA = ∠OBN’ = i [alternate angles]
∠AO’B = ∠CBN = r [corresponding angles]
In AOAB, sin i = \(\frac{A B}{O B}\)
In AO’AB, sin r = \(\frac{A B}{O’ B}\)
As, light ray is travelling from denser medium to rarer medium.
r
μ
d
= \(\frac{sin i}{sin r}\)
or
r
μ
d
= \(\frac{A B}{O’ B}\) × \(\frac{O B}{A B}\) = \(\frac{O B}{O’ B}\)
B is close to A (as angles are very small). So,
OA ≈ OB and O’A ≈ O’B
r
μ
d
= \(\frac{O A}{O’ A}\)
r
μ
d
= \(\frac{\text { Real depth of object }}{\text { Apparent depth of object }}\)
Or
Consider a plane wavefront AB incident at angle i on reflecting surface as shown in figure below
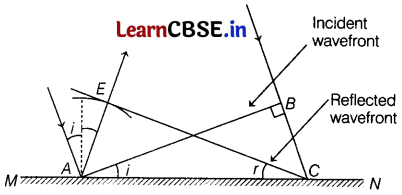
Let v = speed of light in medium
and t = time taken by wavefront to reach point C.
∴ BC = vt
To get reflected wavefront, we draw a sphere of radius vt from point A. Then, the tangent surface CE represents the reflected wavefront.
∴ AE = BC = vt
Now, in triangles ECA and BAC,
AE = BC
∠AEC = ∠ABC = 90°
AC = AC (common)
This means triangles EAC and BAC are congruent.
⇒ ∠ECA = ∠BAC
or i = r
Reflected wavefront makes same angle after reflection as made by incident wavefront.
![]()
Section C
Question 22.
The oscillating electric field is
E
y
= 30 sin [2 × 10
11
t + 300πx] Vm
-1
(i) Obtain the value of the wavelength of the electromagnetic wave. [2]
(ii) Write down the expression for the oscillating magnetic field. [1]
Solution:
(i) Comparing the equation of oscillating electric field with the standard wave equation,
E(x,t) = E
0
sin (ωt + kx)
We find that, propagation constant,
k = 300π rad m
0
and amplitude of oscillating electric field,
E
0
= 30 Vm
-1
.
.-. Wavelength of the electromagnetic wave,
\(\lambda=\frac{2 \pi}{k}=\frac{2 \pi}{300 \pi}=\frac{1}{150}\) m
(ii) The electromagnetic wave is propagating along negative direction of X-axis and electric field is oscillating along Y-axis. As the direction of wave propagation is the direction of E × B, hence magnetic field must be oscillating along negative Z-axis, moreover its amplitude
B
0
= \(\frac{E_0}{c}\) = \(\frac{30}{3×10^8}\) = 10
-7
T
Hence, expression for oscillating magnetic field is
B
z
= 10
-7
sin [2 × 10
11
t + 300πx] T
Question 23.
Define the distance of closest approach. An α-particle of kinetic energy K is bombarded on a thin gold foil. The distance of closest approach is r. What will be the distance of closest approach for an α-particle of double the kinetic energy? [3]
Solution:
Distance of Closest: Approach As the α-particle approaches the nucleus, the electrostatic force of repulsion due to nucleus increases and the kinetic energy of α-particle goes on converting into the electrostatic potential energy.
At a certain distance r from the nucleus, whole of the KE of α-particle converts into electrostatic potential energy and α-particles cannot go further close to nucleus, this distance r
0
is called distance qf closest approach.
At distance of closest approach,
KE of α-particle = Electrostatic potential energy
K = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{(Z e)(2 e)}{r}\)
[∵ charge on α-particle is +2e and charge on nucleus is Ze, where Z is atomic number]
r = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2Ze^2}{K}\)
or r = \(\frac{1}{4 \pi \varepsilon_0} \cdot \frac{2 Z e^2}{\left(\frac{1}{2} m v^2\right)}\)
where, m = mass of α-particle and v = initial velocity of α-particle.
i.e, r ∝ \(\frac{1}{K}\)
Let r
0
be the new distance of closest approach for a twice energetic α-particle.
\(\frac{r_0}{r}=\frac{K}{2 K}=\frac{1}{2}\)
r
0
= \(\frac{r}{2}\)
![]()
Question 24.
(i) Write three characteristic properties of nuclear force. [1]
(ii) Draw a plot of potential energy of a pair of nucleons as a function of their separation. Write two important conclusions that can be drawn from the graph. [2]
Solution:
(i) Some of the important characteristics of these forces are as given below
(a) Nuclear forces among a pair of neutrons, a pair of protons and also between a neutron-proton pair, is approximately the same. This shows that nuclear forces are independent of charge.
(b) The nuclear forces are very short range forces. They are operative upto distances of the order of a few fermi.
(c) The nuclear force is much stronger than the coulomb force acting between charges or gravitational forces between masses.
(ii)
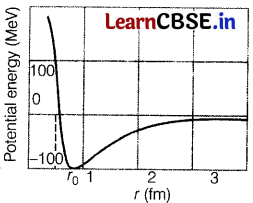
From the plot, it is concluded that potential energy is minimum at a distance r
0
(≈0.8 fin) which means, the force is attractive for distances larger than 0.8 fm and repulsive for the distances less than 0.8 fm between nucleons.
Question 25.
Plot a graph showing temperature dependence of resistivity for metal. How is this behaviour explained? [3]
Solution:
Temperature Dependence of Resistivity
Resistivity of a metal conductor is given by
\(\rho=\rho_0\left[1+\alpha\left(T-T_0\right)\right]\) …..(i)
where, ρ = resistivity at temperature T
and ρ
0
= resistivity at temperature T
0
α = \(\frac{\rho-\rho_0}{\rho_0\left(T-T_0\right)}\) = \(\frac{d \rho}{\rho_0} \cdot \frac{1}{d T}\)
Thus, temperature coefficient of electrical resistivity is also defined as the fractional change in electrical resistivity \(\frac{d \rho}{\rho_0}\) per unit change in temperature dT.
For metals, the value of a is positive, therefore resistivity of metal increases with increase in temperature.
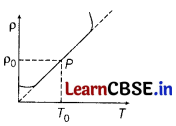
Eq.(i) implies that a graph of p plotted against T would be a straight line. At temperatures much lower than 0°C, the graph deviates considerably from a straight line. Eq.(i) can be used approximately over a limited range of T around any reference temperature T
0
, where the graph can be approximated as a straight line.
Question 26.
Force on a charge due to electric field is given by F
E
= qE and force due magnetic field is given by F
B
= q (v × B). In a certain region of space, both electric and magnetic fields exist mutually perpendicular to each other. If an electron enters this region perpendicular to both E and B and passes out undeflected, find the velocity of the electron. [3]
Solution:
As, the electron enters perpendicular to electric and magnetic field, force due to electric field, F
E
= eE.
This will be along the opposite direction of E.
Force due to magnetic field,
F
B
=e(v × B) = ev sin θ
= evBsin90° =evB (as v l B)
Direction of this force will be given by right hand screw or thumb rule.
As, the electron passes undeflected, the force due to the two fields must be equal in magnitude and opposite in direction.
i.e. F
E
= F
B
⇒ eE = evB ⇒ v = \(\frac{E}{B}\)
So, velocity of electron is E / B.
Question 27.
Three concentric metal shells A, B and C of radius a, b and c(a< b< c) have surface charge densities +σ, -σ and +σ, respectively.
(i) Find the potential of three shells of A, B and C. [1]
(ii) If the shells A and C are at the same potential, then obtain the relation between the radii a, b and c. [2]
Solution:
(i) Potential of three shells
At shell A
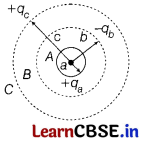
(ii) Relation between the radii


Question 28.
(i) Two circular coils, one of radius r and other of radius R are placed co-axially with their centres coinciding. For R >> r, obtain an expression for mutual inductance of the arrangement. [2]
(ii) The magnetic flux through a coil perpendicular to the plane is given by ϕ = 5t³ +4t² +2t. Calculate induced emf through the coil at t = 2 s. [1]
Or
(i) The current through an AC is I = I
0
(t / τ)
Determine the rms current through the circuit over time interval t = 0 to τ. [1]
(ii) Show that the heat produced in a cycle of AC is same as the heat produced by DC with I = I
rms
. [2]
Solution:
(i) Let r, R be the radius of smaller and bigger coil C
1
and C
2
respectively, carrying current l
1
, and l
2
(as shown below).

(ii) As we know that, e = \(\frac{d \phi}{dt}\),
ϕ = 5t³ +4t² +2t
So, e = latex]\frac{d }{dt}[/latex] (5t³ + 4t² + 2t) = 15t² + 8t + 2
For t = 2 s, e = 15 × 2² + 8 × 2 + 2
= 60 + 16 + 2 = 78 V
Or
(i) The mean square current is

(ii) For an AC, I = I
o
sin ωt
Heat produced in a resistance in small time dt.
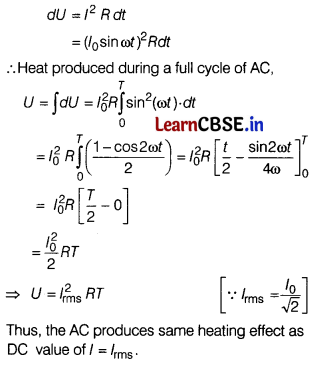
![]()
Section D
[Case Study Based Questions]
Question 29.
Read the following paragraph and answer the questions that follow.
It is an arrangement made by a close contact of n-type semiconductor and p-type semiconductor.There are various methods of forming p-n junction. In one method, an n-type germanium crystal is cut into thin slices called wafers. An aluminium film is laid on an n-type wafer, which is then heated in an oven at a temperature of about 600°C. In this way, p-n junction formed. Biasing is the method of connecting external battery or emf source to a p-n junction diode. A junction of positive terminal connected to positive terminal of battery p-side of the diode and negative terminal to the n-side of the diode.
Moreover, p-n junction diode called dynamic resistance. It is the ratio of small change in forward voltage to the small change in forward current produced.
(i) The conductivity of a semiconductor increases with increases in temperature, because [1]
(a) number density of free current carriers increases
(b) relaxation time increases
(c) both number density of carriers and relaxation time increases
(d) number density of carrier increases, relaxation time decreases but effect of decrease in relaxation time is much less than increase in number density.
Answer:
(d) number density of carrier increases, relaxation time decreases but effect of decrease in relaxation time is much less than increase in number density.
The conductivity of a semiconductor increases with increase in temperature, because the number density of current carrier increases, relaxation time decreases but effect of decrease in relaxation is much less than increase in number density.
(ii) The substance which doped in an intrinsic semiconductor to make p-type semiconductor is [1]
(a) phosphorus
(b) antimony
(c) aluminium
(d) arsenic
Answer:
(c) aluminium
In an intrinsic semiconductor, when an impurity of trivaient group such as aluminium, boron etc. mixed in very small quantity, then the resultant crystal will be p-type semiconductor.
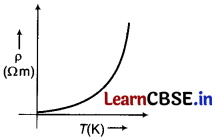
(iii) Which of the following variation of resistivity of Si with temperature is correct? [1]
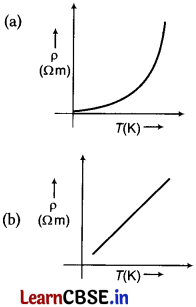
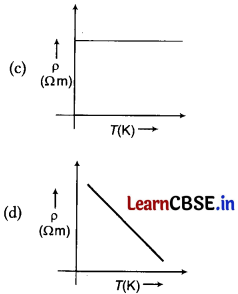
Answer:
Graph of resistivity of Si as a function of temperature is given below (resistivity of metals increases with increase in temperature
Or
When very small current due to minority charge carriers flows across the junction, then it is called [1]
(a) forward current
(b) saturated current
(c) reverse current
(d) None of these
Answer:
(c) reverse current
When a diode is reversed biased, then very small current due to minority charge carriers flows across the junction. This current is called reverse current.
(iv) In an unbiased, p-n junction diode hole, diffuse from the p-region to n-region because
(a) free electrons in the n-region attract them
(b) they moves across the junction by the potential difference
(c) hole concentration in p-region is more as compared
(d) All of the above
Answer:
(c) hole concentration in p-region is more as compared
The diffusion of charge carrier across a junction takes place from the region of higher concentration to lower concentration. In this case, the p-n junction hole diffuse from the p-region to the n-region.
Question 30.
Read the following paragraph and answer the questions that follow.
Combination of thin lenses
Assume two lenses A and B of focal length f
1
and f
2
placed in contact with each other. An object is placed at a point O beyond the focus of the first lens A. The first lens produces an image at Ir which serves as a virtual object for the second lens B, producing the final image at I.
We get focal length, \(\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}+\ldots+\frac{1}{f_n}\)
whereas, magnification of these com-bination of thin lenses,
\(m=m_1 \times m_2 \times m_3 \times \ldots m_n\)
and thin lens formula, \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
(i) Two thin lenses are in contact and the focal length of the combination is 80 cm. If the focal length of one lens is 20 cm, then power of the another lens is [1]
(a) -3.75 D
(b) + 3.75 D
(c) – 4.75 D
(d) + 4.75 D
Answer:
(a) -3.75 D
Combined focal length, f = 80 cm
f
1
= 20 cm, P
2
= ?
p = \(\frac{100}{F}\) = \(\frac{100}{80}\) = 12.5 D
p
1
= \(\frac{100}{f_1}\) = \(\frac{100}{20}\) = 5 D
We know, P = P
1
+ P
2
P
2
= P – P
1
= 1.25 – 5
= -3.75 D
(ii) Two lenses are in contact having focal length 25 cm and – 40 cm. Find total power of this lens. [1]
(a) – 6.67 D
(b) – 2.5 D
(c) + 1.5 D
(d) + 4 D
Answer:
(c) + 1.5 D
Given, f
1
= 25cm, f
2
= -40 cm
P
1
= \(\frac{100}{f_1}\) = \(\frac{100}{25}\) = +4 D
P
2
= \(\frac{100}{f_2}\) = \(\frac{100}{-40}\) = -2.5 D
Total power of lens, P = P
1
+ P
2
P = 4+ (-2.5)
P = 1.5 D
![]()
(iii) A lens is made of two different materials and a point object is placed on the principal axis of this lens. Count the images obtained. [1]
(a) 2
(b) 4
(c) 6
(d) 1
Answer:
(a) 2
If refractive index of each material is different, so the lens will have two different focal length, one for each material. Hence, two images will formed.
(iv) First and second focal lengths of spherical surface of refractive index n are f
1
and f
2
, respectively. The relation between them, is [1]
(a) f
1
= f
2
(b) f
2
= -f
1
(c) f
2
= nf
1
(d) f
2
= -nf
1
Answer:
(b) f
2
= -f
1
When medium is equal on both sides of lens, then the numerical value of both focal length is equal, hence, f2 = -ff
Or
If combination of lenses consist of one convex lens (f1) and one concave lens (-f2), then [1]
(a) \(\frac{1}{f}=\frac{f_1 f_2}{f_2-f_1}\)
(b) \(f=\frac{f_1 f_2}{f_2-f_1}\)
(c) \(f=\frac{f_2-f_1}{f, f_2}\)
(d) \(f=\frac{1}{f_1}+\frac{1}{f_2}\)
Answer:
(b) \(f=\frac{f_1 f_2}{f_2-f_1}\)
For combination of lenses,
\(\frac{1}{f}\) = \(\frac{1}{f_1}+\frac{1}{-f_2}\)
\(\frac{1}{f}\) = \(\frac{1}{f_1}-\frac{1}{f_2}\)
\(f=\frac{f_1 f_2}{f_2-f_1}\)
Section E
Question 31.
(i) Explain using suitable diagram, the difference in the behaviour of a
(a) conductor and
(b) dielectric in the presence of external electric field. Define the terms polarisation of a dielectric and write its relation with susceptibility. [3]
(ii) A thin metallic spherical shell of radius R carries a charge Q on its surface. A point charge Q/2 is placed at its centre C and an another charge +2 Q is placed outside the shell at a distance x from the centre as shown in figure.
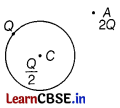
Find
(a) the force on the charge at the centre of the shell and at point A,
(b) the electric flux through the shell. [2]
Answer:
(i) (a) When a capacitor is placed in an external electric field, the free charges present inside the conductor redistribute themselves in such a manner that the electric field due to induced charges opposes the external field within the conductor. This happens until a static situation is achieved, i.e. when the two fields cancel each other and the net electrostatic field in the conductor becomes zero.
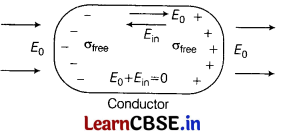
(b) In contrast to conductors, dielectrics are non-conducting substances, i.e. they have no charge carriers. Thus, in a dielectric, free movement of charges in not possible. It turns out that the external field induces dipole moment by stretching molecules of the dielectric. The collective effect of all the molecular dipole moments is the net charge on the surface of the dielectric which. produces a field that opposes the external field. However, the opposing field is so induced, that does not exactly cancel the external field. It only reduces it. The extent of the effect depends on the nature of dielectric.
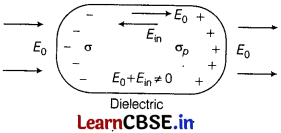
Both polar and non-polar dielectrics develop net dipole moment in the presence of an external field. The dipole moment per unit volume is called polarisation and is denoted by P for linear isotropic dielectrics.
P = χE
where, χ is constant of proportionality and is called electric susceptibility of the electric slab.
(ii) (a) At point C, inside the shell, electric field inside a spherical shell is zero.
Thus, the force experienced by charge at centre C will also be zero.

Or
Two metal spheres, one of radius R and the other of radius 2 R, both have same surface charge density a. They are brought in contact and separated. What will be new surface charge densities on them? [5]
Solution:
Radius of sphere A = R
Surface charge density on sphere A = σ
Radius of sphere B = 2R
Surface charge density on sphere B = σ
Before contact, the charge on sphere A,
Q
1
= Surface charge density × Surface area
⇒ Q
1
= σ ⋅4πR² ……..(i)
Before contact, the charge on sphere B is
Q
2
= Surface charge density × Surface area
Q
2
= σ ⋅4π(2R)² = σ ⋅16πR² …….(ii)
Let after the contact, the charge on A be Q
1
and the charge on B be Q
2
.
According to the conservation of charge, the charge before contact is equal to charge after contact.
Q’
1
+ Q’
2
= Q
1
+ Q
2
Now, from Eqs. (i) and (ii), we get
Q’
1
+ Q’
2
= 4πR²σ + 16πR²σ
= 20πR²σ …..(iii)
As they are in contact. So, they have same potential.


![]()
Question 32.
(i) An alternating emf E = E
0
sin cot is applied as an input in a purely , resistive circuit of resistance R.
(a) What is the current in the circuit? [1]
Answer:
(a) Alternating emf, E = E
0
sin ωt
Current in the circuit, labelled l = \(\frac{E}{R}=\frac{E_0}{R} \sin \omega t\)
or l = l
0
sin ωt
where, l
0
= \(\frac{E_0}{R}\) is the peak value of current. R
(b) What is the phase difference between the emf and the current? [1]
Answer:
Phase difference between the emf and the current is zero.
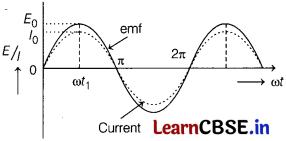
(c) Draw the graphical representation of the emf and the current. [1]
Answer:
Graphical representation of the emf and the current is as shown in figure below
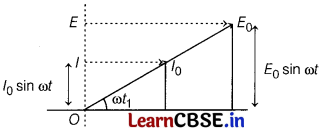
(d) Draw the phasor diagram for a purely resistive circuit. [1]
Answer:
Phasor diagram is as shown in figure below
(ii) A resistance of 10 Q is connected to a AC rated 110 V, 50 Hz, then find the rms current. [1]
Answer:
(ii) Given, resistance, R = 10 Ω
rms value of voltage, E
rms
= 110 V
∴ rms current, I
rms
= \(\frac{E_{\mathrm{rms}}}{R}\) = \(\frac{110}{10}\) = 11A
Or
(i) A diagram of AC generator is shown below
(a) Write the names of labelling P, B
1
or B
2
. [1]
Answer:
(a) Here, P → Armature coil
B
1
or B
2
→ Brushes
(b) What is the principle and working of an AC generator. [2]
Answer:
Principle: An AC generator works on the principle of electromagnetic induction. According to this, whenever there is change in the magnetic flux linked with a coil, an emf is induced across the ends of the coil.
Working: The coil is rotated with a uniform angular speed co in the magnetic field 6 of the permanent/electromagnet such that the axis of coil is perpendicular to magnetic field. As the coil rotates, magnetic flux through it changes due to which an emf is induced across the ends of the coil.
(ii) Deduce the expression for alternating emf induced in the generator when the coil rotates with angular velocity co. [2]
Answer:
Expression for alternating emf
Let θ be the angle between the direction and magnetic field B and area vector A. As, co is the angular speed, then at any time t, θ = ωt
Flux through the coil at any time,
ϕ
B
= BA cos θ = BA cos ωt
From Faraday’s law, the emf induced in rotating a coil of N turns is
E = \(\frac{1}{2}\) = – NBA \(\frac{d}{dt}\) (cos ωt)
Thus, instantaneous emf, E = NBAω sin ωt
This emf will be maximum for sin ωt = ± 1
or at = 90°, 270° and E
max
= E
0
= NBAω
E = E
0
sin ωt
This gives the expression for emf induced. As emf £ is a sine function, it varies periodically as the coil rbtates.
Question 33.
(i) Derive the lens formula, \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\) for a concave lens, using the necessary ray diagram. [3]
(ii) The image of a small electric bulb fixed on the wall of a room is obtained on the opposite wall by means of a large convex lens as shown below.
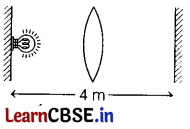
What is the maximum possible focal length of the lens required for this purpose? [2]
Or
Figure shows an equi-convex lens (of refractive index 1.5) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be 50 cm. The liquid is removed and the experiment is repeated. The new distance is measured to be 30.0 cm.
(a) What is the radius of curvature of the equi-convex lens ? [3]
(b) What is the refractive index of the liquid? [2]
Solution:
(i) The formation of image by a concave lens L is shown in figure below
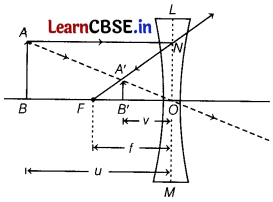
Consider AB as an object and A’B’ is its image. The object is at a distance u from the lens and its image is formed at a distance v.
In triangles ABO and A’B’O are similar,
∴ \(\frac{A B}{A’ B’}=\frac{O B}{O B’}\) ………(i)
Also, triangles A/OF and A’B’Fare similar,
\(\frac{N O}{A’ B’}=\frac{O F}{F B’}\)
But NO = AB
∴ \(\frac{A B}{A’ B’}=\frac{O F}{F B’}\) ………..(ii)
Comparing Eq.s (i) ans (ii), we get
\(\frac{O B}{O B’}\) = \(\frac{O F}{F B’}\)
⇒ \(\frac{O B}{O B’}\) = \(\frac{O F}{O F – O B’}\)
Using sign conventios of coordinate geometry
Let OB = -u,OB’ = -v, OF = -f
∴ \(\frac{-u}{-v}=\frac{-f}{-f+v}\)
or uf – uv = vf or uv = uf – vf
Dividing throughout by uvl, we get
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
This is the required lens formula.
(ii) Let x be the distance between the object and the image.
Given, x = 4 m.
Here, u + y = x
According to lens formula,
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)

Or
Distance of the needle from the lens in the first case
= focal length F of the combination of the convex lens and plano-concave lens formed by the liquid,
i.e. F = 50 cm
Distance measured in second case = Focal lenght of the convex lens, i.e. f
1
= +30 cm
The focal length f
2
of the plano-concave lens is given by
\(\frac{1}{f_1}+\frac{1}{f_2}=\frac{1}{F}\)
\(\frac{1}{f_2}=\frac{1}{F}-\frac{1}{f_1}\) = \(\frac{1}{50}-\frac{1}{30}\) = \(\frac{3-5}{150}\)
⇒ \(\frac{1}{f_2}=\frac{-2}{150}\)
∴ f
2
= -75 cm
(a) Now, for the equi-convex lens, we have
R
1
= R, R
2
= -R, f = 30 cm, μ = 1.5
Using lens Maker’s formula,
\(\frac{1}{f}=(\mu-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
or \(\frac{1}{30}=(1.5-1)\left[\frac{1}{R}+\frac{1}{R}\right]\) = 0.5 × \(\frac{2}{R}\)
or R = 0.5 x 2 x30 cm = 30 cm
(b) For plano-convex lens, f = -75 cm
For concave surface, R
1
=-R = -30 cm
For plane surface, R
2
= ∞
As \(\frac{1}{f}=(\mu-1)\left[\frac{1}{R_1}-\frac{1}{R_2}\right]\)
\(\frac{1}{-75}=(\mu-1)\left[\frac{1}{-30}-\frac{1}{∞}\right]\)
or μ – 1 = \(\frac{-30}{-75}\) = \(\frac{2}{5}\)
or μ = 1 + \(\frac{2}{5}\) = \(\frac{7}{5}\)
μ = 1.4