Students must start practicing the questions from CBSE Sample Papers for Class 10 Physics with Solutions Set 2 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Physics Set 2 with Solutions
Time : 3 hrs
Max. Marks : 70
Instructions
1. There are 35 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. Section A contains eighteen MCQ of 1 mark each, Section B contains seven questions of two marks each. Section C contains five questions of three marks each. Section D contains three long questions of five marks each and Section E contains two case study based questions of 4 marks each.
4. There is no overall choice. However, an internal choice has been provided in Section B, C, D and E. You have to attempt only one of the choices in such questions.
5. Use of calculators is not allowed.
SECTION A
False
Question 1.
The magnitude of the electric field due to a point charge object at a distance of 4.0 m is 9 N/C. From the same charged object, the electric field of magnitude 16 N/C will be at a distance of
(a) 1 m
(b) 2 m
(c) 3 m
(d) 6 m
Answer:
(b) 2 m
Given that, E = \(\frac{K×q}{r^2}\) (∵ K = 9 × 10
9
Nm
2
/C
2
)
9 = \(\frac{(9 × 10^9) × q }{(4.0)^2}\)
q = 8.0 × 10
9
C
Now, electric fieid has a magnitude of 16 N/C.
16 = \(\frac{\left(9 \times 10^9\right)\left(8.0 \times 10^{-6}\right)}{r^2}\)
r = \(\sqrt{\left(9 \times 10^9\right) \times\left(8.0 \times 10^{-6}\right) / 16}\)
r = 2.0 m
The electric field of magnitude 16 N/C will be at a distance of 2.0 m from the charged object.
Question 2.
A point P lies at a distance x from the mid-point of an electric dipole on its axis. The electric potential at point P is proportional to
(a) \(\frac{1}{x^2}\)
(b) \(\frac{1}{x^3}\)
(c) \(\frac{1}{x}\)
(d) \(\frac{1}{x^1/2}\)
Answer:
(a) \(\frac{1}{x^2}\)
The electric potential of dipole is given by
V = \(\frac{1}{x^2}\)
Electric potential at a point w1′ eh lies at a distance x from the mid-point of the dipole will be
proportional to \(\frac{1}{x^2}\)
Question 3.
A current of 0.8 A flows in a conductor of 40 f2 for 1 min. The heat produced in the conductor will be
(a) 1445 J
(b) 1536 J
(c) 9J
(d) 1640 J
Answer:
(b) 1536 J
Given that, I = 0.8 A
Resistance = 40 Ω for 1 min
Heat produced in the conductor 9 64
= (0.8)
2
× 40 × 60 = \(\frac{64}{100}\) × 40 × 60
= 64 × 4 × 6 = 1536 J
![]()
Question 4.
A cell of emf E is connected across an external resistance R . When current / is drawn from the cell the, potential difference across the electrodes of the cell drops to V. The internal resistance r of the cell is
(a) \(\left(\frac{E-V}{E}\right) R\)
(b) \(\left(\frac{E-V}{R}\right)\)
(c) \(\frac{(E-V) R}{I}\)
(d) \(\left(\frac{E-V}{V}\right) R\)
Answer:
(d) \(\left(\frac{E-V}{V}\right) R\)
Let the current in the circuit, I = V / R
Across the cell, E = V + Ir
⇒ r = \(\left(\frac{E-V}{I}\right) R\) = \(\left(\frac{E-V}{V/R}\right) R\) = \(\left(\frac{E-V}{V}\right) R\)
Question 5.
Beams of electrons and protons move parallel to each other in the same direction. They
(a) attract each other
(b) repel each other
(c) neither attract nor repel
(d) force of attraction or repulsion depends upon speed of beams.
Answer:
(b) repel each other
False
Question 6.
A long strength wire of radius a carries a steady current I. The current is uniformly distributed across its area of cross-section.
The ratio of magnitude of magnetic field B
1
at \(\frac{a}{2}\) and B
2
at distance 2a is
(a) \(\frac{1}{2}\)
(b) 1
(c) 2
(d) 4
Answer:
(b) 1
For a point inside the solid cylinder,

Question 7.
E and B represent the electric and the magnetic field of an electromagnetic wave, respectively. The direction of propagation of the wave is along
(a) B
(b) E
(c) E × B
(d)B × E
Answer:
(c) E × B
The direction of propagation of the electromagnetic wave is always perpendicular to the plane in which E and B lies.
Hence, c = E × B
Option (c) is the correct.
Question 8.
A ray of monochromatic light propagating in air is incident on the surface of water. Which of the following will be the same for the reflected and refracted ray?
(a) Energy carried
(b) Speed
(c) Frequency
(d) Wavelength
Answer:
(c) Frequency
![]()
Question 9.
A beam of light travels from air into a medium. Its speed and wavelength in the medium are 1.5 × 10
8
m/s and 230 nm, respectively. The wavelength of light in air will be
(a) 230 nm
(b) 345 nm
(c) 460 nm
(d) 690 nm
Answer:
(c) 460 nm

Question 10.
Which one of the following metals does not exhibit emission of electrons from its surface when irradiated by visible light ?
(a) Rubidium
(b) Sodium
(c) Cadmium
(d) Costume
Answer:
(c) Cadmium
Question 11.
A hydrogen atom makes a transition from n = 5 to n = 1 orbit. The wavelength of photon emitted is λ. The wavelength of photon emitted when it makes a transition from n = 5 to n = 2 orbit is
(a) \(\frac{8}{7}\) λ
(b) \(\frac{16}{7}\) λ
(c) \(\frac{24}{7}\) λ
(d) \(\frac{32}{7}\) λ
Answer:
(d) \(\frac{32}{7}\) λ
n = 5 to n = 1

Question 12.
The curve of binding energy per nucleon as a function of atomic mass number has a sharp peak for helium nucleus. This implies that helium nucleus is
(a) radioactive
(b) unstable
(c) easily Fissionable
(d) more stable nucleus than its neighbours
Answer:
(d) more stable nucleus than its neighbours
Question 13.
In an extrinsic semiconductor, the number density of holes is 4 × 10
20
m
-3
. If the number density of intrinsic carriers is 1.2 × 10
15
m
-3
, the number density of electrons in it is
(a) 1.8 × 10
9
m
-3
(b) 2.4 × 10
10
m
-3
(c) 3.6 × 10
9
m
-3
(d) 3.2 × 10
10
m
-3
Answer:
(c) 3.6 × 10
9
m
-3
Given that, number density of holes
= 4 × 10
20
m
-3
Number density of intrinsic carriers
(n
i
) =1.2 × 10
15
m
-3
Then,
Number density of electrons, (n
i
)
2
= p × n
where, p is the number density of holes and n is the number density of electrons.
4 × 10
20
× n = (1.2 × 10
15
)
2
We get, n = \(\frac{\left(1.2 \times 10^{15}\right)^2}{4 \times 10^{20}}\)
= 3.6 × 10
9
m
-3
![]()
Question 14.
Pieces of copper and of silicon are initially at room temperature. Both are heated to temperature T. The conductivity of
(a) both increase
(b) both decrease
(c) copper decreases and silicon increases
(d) copper increases and silicon decreases
Answer:
(d) copper increases and silicon decreases
True
Question 15.
The formation of depletion region in a p-n junction diode is due to
(a) movement of dopant atoms
(b) diffusion of both electrons and holes
(c) drift of electrons only
(d) drift of holes only
Answer:
(b) diffusion of both electrons and holes
Directions (Q. Nos. 16-18) In question number 16 to 18 two statements are given-one labelled Assertion (A) and the other laballed Reason (R). Select the correct answer to these questions from the codes (a), (b), (c) and (d) as given below.
(a) Both Assertion (A) Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) Reason (R) are true and Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true and Reason (R) is false.
(d) Assertion (A) is false and Reason (R) is also false.
Question 16.
Assertion (A) Diamagnetic substances exhibit magnetism.
Reason (R) Diamagnetic materials do not have permanent magnetic dipole moment.
Answer:
(a) Both Assertion (A) Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
False
Question 17.
Assertion (A) Work done in moving a charge around a closed path in an electric field is always zero.
Reason (R) Electrostatic force is a conservative force.
Answer:
(a) Both Assertion (A) Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
False
Question 18.
Assertion (A) In Young’s double slit experiment, all fringes are of equal width.
Reason (R) The fringe width depends upon wavelength of light (A) used, the distance of screen from plane of slits (D) and slits separation (d).
Answer:
(a) Both Assertion (A) Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
True
![]()
SECTION B
Question 19.
Briefly explain, why and how a galvanometer is converted into an ammeter.
Answer:
Conversion of a Galvanometer into Ammeter A low resistance galvanometer is known as an ammeter. An ammeter is used to measure the current in a circuit in amperes.
To convert a galvanometer into ammeter, its resistance needs to be lowered, so that maximum current can pass through it and it can give exact reading.
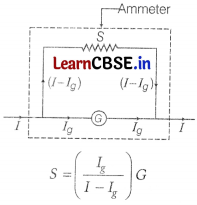
where, I = total current in circuit,
G = resistance of the galvanometer,
S = resistance of the shunt (low resistance) and
I
g
= current through the galvanometer.
(full scale deflection current)
The effective resistance of shunted galvanometer,
i.e. ammeter will be R
p
= \(\frac{GS}{G+S}\)
The resistance of an ideal ammeter is zero.
Question 20.
(i) How are infrared waves produced ? Why are these waves referred to as heat waves? Give any two uses of infrared waves.
Or
(ii) How are X-rays produced ? Give any two uses of these.
Answer:
(i) Infrared waves produced from the heat radiating bodies and molecules. Because they have high penetration power. Its frequency range is 3 × 10
9
Hz to 4 × 10
14
Hz.
Uses of infrared waves are
(a) These are used in satellite for army purpose.
(b) These are used for producing dehydrated fruits.
Or
(ii) X-rays are produced due to sudden deceleration of fast moving electrons when they collide and interact with target anode. Uses of X-rays are
(a) They are used in engineering to detect fault, crack on bridge, testing of welds.
(b) These are used in scientific research.
Question 21.
In the given figure the radius of curvature of curved face in the plano-convex and the plano-concave lens is 15 cm each. The refractive index of the material of the lenses is 1.5. Find the final position of the image formed.
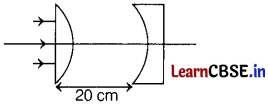
Answer:
For plano-convex lens,

Question 22.
What happens to the interference pattern when two coherent sources are
(i) infinitely close and
(ii) far apart from each other.
Answer:
(i) No interference pattern is detected. When two coherent sources are infinitely close.
(ii) If the sources are far apart d is large, so fringe width (P) will be so small that the fringes are not resolved and they do not appear separate. That’s why, the interference pattern is not detected for large separation of coherent sources.
![]()
Question 23.
(i) What is meant by ionisation energy ?
Write its value for hydrogen atom.
Or
(ii) Define the term mass defect. How is it related to stability of the nucleus ?
Answer:
(i) The minimum energy required to free the
electron from the ground state of H-atom is called ionisation energy.
The ionisation energy for H-atom,
E = E
∞
– E
1
E = 0 – (-13.6)
E = 13.6 eV
Paraphrase: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Ora
(ii) The difference between the sum of the rest masses of its constituent nucleons and the rest mass of a nucleus is called mass defect.
Mass defect is related to the stability of the nucleus because the magnitude of the mass defect is proportional to the nuclear binding energy, both values indicate the stability of the nucleus. Just as a molecule is more stable (lower in energy) than its isolated atoms, a nucleus is more stable than its isolated components.
Question 24.
Draw energy band diagram for an n-type and p-type semiconductor at T > 0K.
Answer:
Energy Band in Extrinsic Semiconductors: In extrinsic semiconductors, additional energy states due to donor impurities (E
D
) and acceptor impurities (EA) also exist. In the energy band diagram of n-type semiconductor, the donor energy level ED is slightly below the bottom Ec of conduction band and the electrons from this level move into conduction band with very small supply of energy.
In p-type semiconductors, the acceptor energy level EA is slightly above the top energy level Ev of the valence band. With very small supply of energy an electron from the valence band can jump to the level EA and ionise the acceptor negatively.
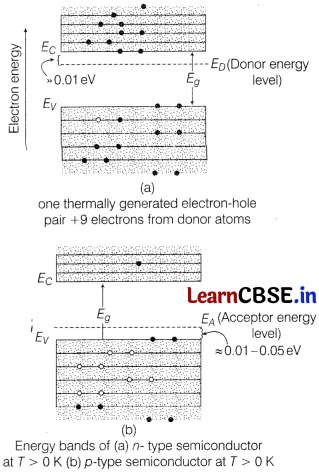
Question 25.
Answer the following giving reasons :
(i) A p-n junction diode is damaged by a strong current.
(ii) Impurities are added in intrinsic semiconductors.
Answer:
(i) A p-n junction diode is get damaged by a strong current because it gets heat up.
(ii) Intrinsic semiconductors are pure semiconductors. We add the impurities in functionality and increase its conductivity.
![]()
SECTION C
Question 26.
(i) Two charged conducting spheres of radii a and b are connected to each other by a wire. Find the ratio of the electric fields at their surfaces.
Or
(ii) A parallel plate capacitor A of capacitance C is charged by a battery to voltage V. The battery is disconnected and an uncharged capacitor B of capacitance 2C is connected across A. Find the ratio of
(a) final charges on A and B.
(b) total electrostatic energy stored in A and B finally and that stored in A initially.
Answer:
(i) As the two conducting spheres are connected to each other by a wire, the charge always flows from higher potential to lower potential till both have same potential.

Paraphrase: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Ora
(ii) (a)
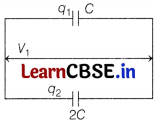
∴ q
1
+ q
n
= Q
⇒ q
1
+ q
n
= CV
⇒ CV
1
+ 2CV
1
= CV
⇒ V
1
= V/3
∴ q
1
= CV
1
= C × \(\frac{V}{3}\) = Q/3 (for A)
and q
2
= 2CV
1
= 2C × V/3 = 2Q/3 (for B)
(b)

Question 27.
Define current density and relaxation time. Derive an expression for resistivity of a conductor in terms of number density of charge carriers in the conductor and relaxation time.
Answer:
Current Density: The current density at a point in a conductor is defined as the amount of current flowing normally through unit area around that point of conductor.
If a current I is distributed uniformly over the cross-section area A of a conductor, then the current density at that point is
\(\mathcal{F}\) = \(\frac{I}{A}\)
It is a vector quantity and the SI unit of current density is Am
2
.
Relaxation Time: The average time-interval between two successive collision is called the relaxation time of the electron. It is denoted by τ.
Its value is the order of 10
-14
S.
Expression for resistivity of a conductor We have current in conductor, I = neAν
d
Drift velcoity, ν
d
= \(\frac{eE}{m}\) . τ

Question 28.
A series C-R circuit with R = 200 Ω and C = (50/π)μF is connected across an AC source of peak voltage ε
0
= 100 V and frequency v = 50 Hz. Calculate
(i) impedance of the circuit Z,
(ii) phase angle ϕ and
(iii) voltage across the resistor.
Answer:
Given that, R = 200 Ω
C = \(\frac{50}{\pi}\) μF = \(\frac{50}{\pi}\) × 10
-6
F
ε
0
= 100 V
ν = 50 Hz
(i) impedance of the circuit Z

(ii) phase angle ϕ and
tan ϕ = \(\frac{Z}{R}\) = \(\frac{200}{200}\) = 1
ϕ = tan
-1
(1)
ϕ = 45°
(iii) voltage across the resistor
V
rms
= \(\frac{\varepsilon_0}{\sqrt{2}}=\frac{100}{\sqrt{2}}=70.72 \mathrm{~V}\)
![]()
Question 29.
Define critical angle for a given pair of media and total internal reflection. Obtain the relation between the critical angle and refractive index of the medium.
Answer:
Critical angle for a pair of given media in contact can be defined as, “the angle of incidence in denser medium for which angle of refraction in rarer is 90°”. If the angle of incidence of light, when travelling from a denser medium to a rarer medium, is greater than the critical angle, then total internal reflection takes place.
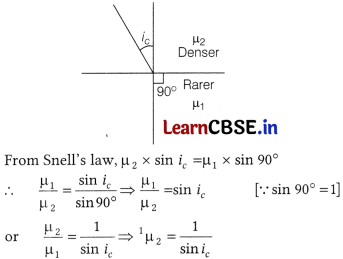
Question 30.
(i) (a) Distinguish between nuclear fission and fusion giving an example of each.
(b) Explain the release of energy in nuclear fission and fusion on the basis of binding energy per nucleon curve.
Or
(ii) (a) How is the size of a nucleus found experimentally ? Write the relation between the radius and mass number of a nucleus.
(b) Prove that the density of a nucleus is independent of its mass number.
Answer:
(i) (a) Differences between Nuclear Fission and Nuclear Fusion.
I. Fission is the splitting of large nucleus into two or more smaller ones, on the other hand, fusion is the combining of two or more lighter nuclei to form a heavier more stable nucleus.
II. Fission does not normally occur in nature but fusion occurs in stars such as the sun.
III. Fission requires critical mass of the substance and high speed neutrons but in fusion, high density and high temperature environment are required.
IV. In fission, energy released is million times greater than in chemical reactions, but lower than energy released by nuclear fusion.
V. Uranium is the primary fuel for fission reaction and hydrogen isotopes are the primary fuel in nuclear fusion reaction.
VI. Atom bomb is based upon the nuclear fision while hydrogen bomb is based upon the fusion of heavy hydrogen nuclei.
(b) Binding Energy Curve or Releasing Binding Energy It is a plot of the binding energy per nucleon £bn versus the mass number A for a large number of nuclei.
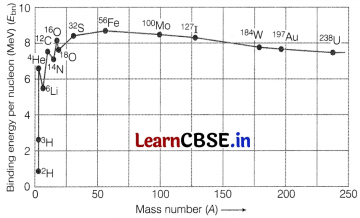
The following are the features of the plot I. Average BE/nucleon for lighter nuclei; like
1
H
1
,
1
H
2
,
1
H
3
is small.
II. For mass numbers ranging from 2 to 20, there are sharply defined peaks corresponding to
2
He
4
,
6
C
12
,
8
O
16
, etc.
These peaks indicate that these nuclei are relatively more stable than the other nuclei in their neighbourhood.
III. The BE curve has a broad maximum peak in the range A =30 to A = 120. It is practically constant corresponding to average binding energy per nucleon as 8.5 MeV. The peak value for the above given range is 8.8 MeV per nucleon for
26
Fe
56
.
IV. As the mass number increases, the BE/nucleon decreases gradually falling to about 7.6 MeV per nucleon for
92
Fe
238
.
This decrease may be due to coulomb repulsion between the protons. The heavy nuclei are therefore, relatively less stable.
Conclusions: Following conclusions are obtained from the graph
I. A very heavy nucleus A = 240 has lower E
bn
compared to that of a nucleus with A =120. Thus, if a nucleus A= 240 breaks into two A =120 nuclei, nucleons get more tightly bound. Energy would be released in this process (nuclear fission).
II. When two light nuclei (A ≤ 10) combine to form a heavier nucleus, E
bn
of fused – heavier nuclei is more than the £bn of
lighter nuclei. Energy would be released in this process (nuclear fusion).
Or
(ii) (a) The size of the nucleus has been measured with the help of a variety of experiments involving the scattering of particles such as neutrons, protons, electrons, etc. It is found that the volume of the nucleus is directly proportional to the number of nucleons (mass number) constituting nucleus.
If R is the radius of the nucleus having mass number A, then
\(\frac{4}{3}\)πR
3
∝ A ⇒ R ∝ A
1/3
=> R = R
0
A
1/3
It is the relation between the radius and mass number of a nucleus.
where, R
0
= 1.2 × 10
-15
m is the range of nuclear size.
It is also known as nuclear unit radius.
Owing to the small size of the nucleus, fermi (fm) is found to be a convenient unit of length in nuclear physics.
It is given as, 1 fermi (fm) =10
-15
m
(b) Density of nuclear matter is the ratio of mass of nucleus to its volume.
If m is the average mass of a nucleon and A is the mass number of element, then the mass of nucleus = mA. If R is the nuclear radius, then
volume of nucleus = \(\frac{4}{3}\)πR
3
= \(\frac{4}{3}\)π(R
0
A
1/3
)
3
As, density of nuclear matter
= \(\frac{\text { mass of nucleus }}{\text { volume of nucleus }}\)
ρ = \(\frac{mA}{\frac{4}{3} \pi R_0^3 A}\)
ρ = \(\frac{3 m}{4 \pi R_0^3}\)
Thus, the density of nucleus is a constant, independent of A, for all nuclei.
![]()
SECTION D
Question 31.
(i) (a) Use Gauss’law to obtain an expression for the electric field due to an infinitely long thin straight wire with uniform linear charge density λ.
(b) An infinitely long positively charged straight wire has a linear charge density λ. An electron is revolving in a circle with a constant speed v such that the wire passes through the centre and is perpendicular to the plane of the circle. Find the kinetic energy of the electron in terms of magnitudes of its charge and linear charge density λ on the wire.
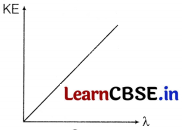
(c) Draw a graph of kinetic energy as a function of linear charge density λ.
Or
(ii) (a) Consider two identical point charges located at points (0, 0) and (a,0).
I. Is there a point on the line joining them at which the electric field is zero?
II. Is there a point on the line joining them at which the electric potential is zero?
Justify you answers for each case.
(b) State the significance of negative value of electrostatic potential energy of a system of charges.
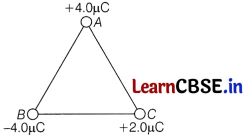
Three charges are placed at the corners of an equilateral triangle ABC of side 2.0 m as shown in figure. Calculate the electric potential energy of the system of three charges.
Answer:
(i) (a) Consider an infinitely long thin straight wire with uniform linear charge density (λ).

(b) Infinitely long charged wire produces a radical electric field,

(c) The a graph is as follows
(ii) (a) I.

Yes, there is a mid-point (\(\frac{a}{2}\)) on the line between the two identical point charges, where the electric potential is zero.
II. No, potential cannot be zero because it is a scalar quantity.
(b) The significance of a negative value of electrostatic potential energy indicates that the system of charges is in a stable configuration. When the potential energy is negative, it means that work has been done to bring the charges closer together and they are bound in a more stable arrangement.
Given, q
1
= 4uC = 4 × 10
-6
C.
q
2
= -4uC = -4 × 10
-6
C.
and q
3
= 2uC = 2 × 10
-6
C.
d = 2 cm = 2 × 10
-2
m

![]()
Question 32.
(i) (a) Define coefficient of self-induction. Obtain an expression for self-inductance of a long solenoid of length /, area of cross-section A having N turns.
(b) Calculate the self-inductance of a coil using the following data obtained when an AC source of frequency
Hz and a DC source is applied across the coil.
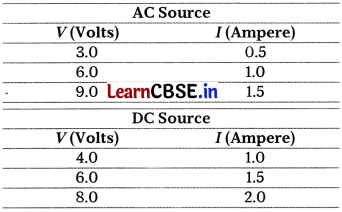
Or
(ii) (a) With the help of a labelled diagram, describe the principle and working of an AC generator. Hence, obtain an expression for the instantaneous value of the emf generated.
(b) The coil of an AC generator consists of 100 turns of wire each of area 0.5 m2. The resistance of the wire is 100 Q. The coil is rotating in a magnetic field of 0.8 T perpendicular to its axis of rotation, at a constant angular speed of 60 rad/s. Calculate the maximum
emf generated and power dissipated in the coil.
Answer:
(i) (a) The coefficient of self-induction of a coil is numerically equal to the number of magnetic flux linkages with the coil when unit current is flowing through the coil. Its SI unit is henry (H).
Or
The coefficient of self-induction of a coil is numerically equal to the emf induced in the coil when the rate of change of current in the coil is unity.
Self-Inductance of Long Solenoid: A long solenoid is one whose length is very large as compared to its area of cross-section. The magnetic field B at any point inside such a solenoid is practically constant and is given by
B = \(\frac{\mu_0 N I}{l}\) = μ
0
nI [∵ n = N/l] …..(i)
where, 0 = magnetic permeability of free space,
N = total number of turns in the solenoid,
l = length of the solenoid
and n = number of turns per unit length.
∴ Magnetic flux through each turn of the solenoid, ϕ
= B × area of the each turn
ϕ = latex]=\left(\mu_0 \frac{N}{l} I\right) A[/latex]
where, A = area of each turn of the solenoid.
Total magnetic flux linked with the solenoid
= Flux through each turn × Total number of turns
Nϕ = μ
0
\(\frac{N}{l}\) IA × N ……..(ii)
If L is coefficient of self-inductance of the solenoid, then
Nϕ = LI
From Eqs. (ii) and (iii), we get
LI = μ
0
\(\frac{N}{l}\) IA × N or L = \(\frac{\mu_0 N^2 A}{l}\)
If core of any other magnetic material p is placed, then
μ = μ
0
μ
r
[ μ
r
= relative magnetic permeability]
L = \(\frac{\mu_0 \mu_r N^2 A}{l}\)
(b)

Paraphrase: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Oracle: Ora
(ii) (a) AC Generator: It is a device which is used to convert mechanical energy into electrical energy.
Principle: It is based on the phenomenon of electromagnetic induction. The emf is induced in the rotating coil as flux is changing due to angle 0 between B and A variation.
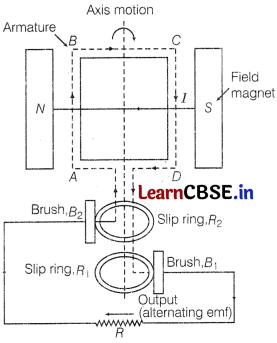
Theory and Working: As the armature of coil is rotated in uniform magnetic field,the magnetic flux linked with the coil changes and an emf is induced in the coil. Hence current flow in it.
Suppose the coil is rotating clockwise and is horizontal of some instance of time. At this instant, the arm AB of the coil is moving up and the arm CD is moving down.
According to Fleming’s right hand rule, the current flows from A to B in the arm AB and C to D in the arm CD.
The brush B
1
at which the current is entering the external circuit is positive relative to the brush B
2
at which the current is leaving the external circuit. During the time the coil rotates to the vertical position, the current in the armature will flow in the direction ABCD. Now the coil ABCD reaches the vertical position, the arms AD and CD move momentarily parallel to the field. So, in vertical position, the induced emf (current) is zero.
After half the rotation of coil, the arm AB moves down and the arm CD moves up. The current flow from B to A in arm AB and D to C in the arm CD.
The brush B
2
is now positive relative to B
1
and remains so long as the coil reaches the vertical position again.
After this, B
1
is again positive relative to B
2
.
Hence, induced current in the external circuit changes direction after every half rotation of the coil. Hence, the current induced is alternating in a nature. Instantaneous value of the emf Consider a coil of N turns and area A being rotated at a constant angular velocity co in a magnetic field B.
When the normal to the coil is at an angle θ to the field, the magnetic flux through the coil is given by
ϕ = BAN cos θ
ϕ = BAN cos ωt (θ = ωt)
Emf E = \(-\frac{d \phi}{d t}\) = \(\frac{d(B A N \cos \theta)}{d t}\)
E = BANω sin (ωt)
when θ = ωt = 90°
E
max
= BANω
(b) maximum emf produced in the coil,
e
0
= NBAω
= 100 × 0.8 × 0.5 × 60
= 2400 V …….(i)
∴ I
0
= e
0
/R = \(\frac{2400}{100}\) = 24 A
∴ Power dissipated, P = e
0
× I
0
= 2400 × 24 = 57600
= 576 × 10² W
![]()
Question 33.
(i) (a) State Huygens’ principle. With the help of a diagram, show how a plane wave is reflected from a surface. Hence, verify the law of reflection.
(b) A convex lens of focal length 12 cm produces three times magnified real image. Find the distance between object and image.
Or
(ii) (a) Draw a labelled ray diagram showing the image formation by a refracting telescope. Define its magnifying power. Write two limitations of a refracting telescope over a reflecting telescope.
(b) The focal lengths of the objective and the eye piece of a compound microscope are 1.0 cm and 2.5 cm, respectively. Find the tube length of the microscope for obtaining a magnification of 300.
Answer:
(i) (a) Huygens’ Principle Each point on the given wavefront (called primary wavefront) is the source of a secondary disturbance (called secondary wavelets) and the wavelets emanating from these points spread out in all directions with the speed of the wave.
The speed with which the wavefront moves outwards from the source is called the speed of the wave. The energy of the wave travels in a direction perpendicular to the wavefront.
Reflection at a Plane Surface: Let 1, 2, 3 be the incident rays and f, 2′, 3′ be the corresponding reflected rays.
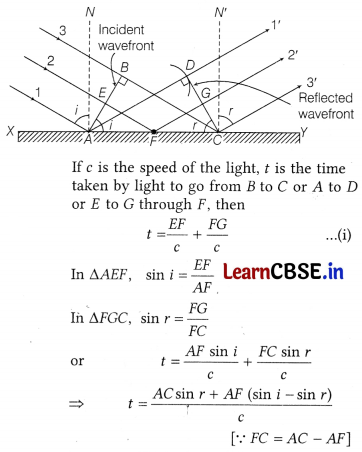
For rays of light from different parts on the incident wavefront, the values of AF are different. But light from different points of the incident wavefront should take the same time to reach the corresponding points on the reflected wavefront.
So, t should not depend upon AF.This is possible only, if
sin i – sin r = 0
i.e, sin i = sin r
or ∠i = ∠r
which is the first law of reflection. Further, the incident wavefront AB, the reflecting surface XY and the reflected wavefront CD are all perpendicular to the plane of the paper.
Therefore, incident ray, normal to the mirror XY and reflected ray all lie in the plane of the paper. This proves the
second law of reflection.
(b) ∴ \(\frac{1}{v}\) – \(\frac{1}{u}\) = \(\frac{1}{12}\)
⇒ \(\frac{u-v}{uv}\) = \(\frac{1}{12}\)
∴m = \(-\frac{v}{u}\) = 3 = v = -3u
∵ \(\frac{1}{2}\) = \(\frac{1}{12}\)
⇒ u = -16 cm
∴ v = 48 cm
So, u – v = 64 cm
(ii) (a) An astronomical telescope is an optical instrument which is used for observing distinct images of heavenly bodies like stars, planets, etc., when the final image is formed at infinity.
Astronomical telescope has two convex lenses coaxially separated by some distance. The lens towards the object is called objective and has much larger aperture than the eyepiece of the lens towards the eye.
Working Light from the distant object enters the objective and real image is formed at second focal point of objective. The eyepiece magnifies this image producing a final inverted image.
Case I When the final image is formed at infinity

Case II When final image is formed at near point

Advantages of Reflecting Telescope over Refracting Telescope
For astronomical telescope, the mirror affords several advantages over the objective lens.
I. A mirror is easier to produce with a larger diameter, so that it can intercept rays crossing a larger area and direct them to the eyepiece.
II. The mirror can be made parabolic to reduce spherical aberration
(b) ∴ m = \(\frac{1}{2}\)
⇒ 300 = \(\frac{1}{2}\) ⇒ 300 = -L(11)
⇒ |L| = \(\frac{300}{11}\) cm
![]()
SECTION E
False
Question 34.
(i) Consider the experimental set-up shown in the figure. This jumping ring experiment is an outstanding demonstration of some simple laws of Physics. A conducting non-magnetic ring is placed over the vertical core of a solenoid. When current is passed through the solenoid the ring is thrown off.
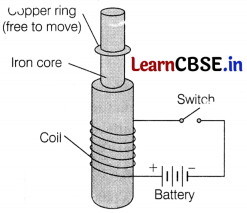
Answer the following questions
(a) Explain the reason of jumping of the ring when the switch is closed in the circuit.
(b) What will happen, if the terminals of the battery are reversed and the switch is closed? Explain.
(c) Explain the two laws that help us understand this phenomenon.
Or
(ii) Briefly explain various ways to increase the strength of magnetic field produced by a given solenoid.
Answer:
(i) (a) Magnetic flux change in the coil due to which induced current play a role but this current oppose the change in flux which cause jumping of the ring when the switch is closed.
(b) Polarity of current change and direction of induced emf also change.
(c) There are two laws
I. Faraday’s first law Whenever the amount of flux linked with a circuit, an emf is induced in the circuit. This induced emf persists as long as the change in magnetic flux continues.
Faraday’s second law The magnitude of the induced emf is equal to the time rate of change of flux.
Induced flux, ε = \(-\frac{d \phi}{dt}\)
II. Lenz law This law gives us the direction of induced emf. According to this law, the direction of induced emf in a circuit is such that it opposes the change in magnetic flux.
Or
(ii) As we know, magnetic field, B = μ
0
nI
I. Increase or change in number of turns of the cell.
II. Increase the value of current.
III. By placing soft iron inside the solenoid.
Question 35.
(i) Figure shows the variation of photoelectric current measured in a photo cell circuit as a function of the potential difference between the plates of the photo cell when light beams A,B,C and D of different wavelength are incident on the photocell. Examine the given figure and answer the following questions:
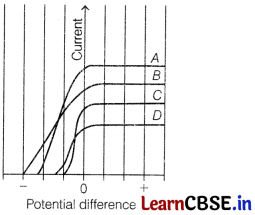
(a) Which light beam has the highest frequency and why ?
(b) Which light beam has the longest wavelength and why ?
(c) Which light beam ejects photoelectron with maximum momentum and why ?
Or
(ii) What is the effect on threshold frequency and stopping potential on increasing the frequency of incident beam of light ? Justify your answer.
(a) A has the highest frequency because A having lowest wavelength and highest photocurrent. Thus, A will be highest.
E = hv = \(\frac{h c}{\lambda}\)
(b) D light beam has the longest wavelength because B having lowest frequency and lowest photocurrent. Thus, D will be lowest.
(c) A light beam ejects photoelectron with maximum momentum due to having highest frequency which is highest as compared to threshold frequency.
ϕ = \(\frac{h v}{c}=\frac{h}{\lambda}\)
Maximum momentum means having lowest frequency.
Or
(ii) As we know, stopping potential
eV
0
= hv
incident
– ϕ, where ϕ is the work function of the metal surface and vincident is the frequency of incident radiation. Thus, stopping potential increase with increase in frequency of incident radiation. If incident frequency above or below, then threshold frequency no photoelectric emission occurs.