Students must start practicing the questions from CBSE Sample Papers for Class 12 Physics with Solutions Set 10 are designed as per the revised syllabus.
CBSE Sample Papers for Class 12 Physics Set 10 with Solutions
Time : 3 hrs
Max. Marks : 70
Instructions
1. There are 33 questions in all. All questions are compulsory.
2. This question paper has five sections : Section A, Section B, Section C, Section D and Section E.
3. All the sections are compulsory.
4. Section A contains sixteen questions, twelve MCQ and four Assertion Reasoning based of 1 mark each, Section B contains five questions of two marks each, Section C contains seven questions of three marks each, Section D contains two case study based questions of four marks each and Section E contains three long answer questions of five marks each.
5. There is no overall choice. However, an internal choice has been provided in one question in Section B, one question in Section C, one question in each CBQ in Section D and all three questions in Section E. You have to attempt only one of the choices in such questions.
6. Use of calculators is not allowed.
7. You may use the following values of physical constants where ever necessary.
(i) c = 3 × 10
8
m/s
(ii) m
e
= 9.1 × 10
-31
kg
(iii) e = 1.6 × 10
-19
C
(iv) µ
0
= 4π × 10
-7
TmA× 10
-1
(v) h = 6.63 × 10
-34
Js
(vi) ε
0
= 8.854 × 10
-112
C
2
N
-1
m
-2
(vii) Avogadro’s number = 6.023 × 10
23
per gram mole
Section A
Question 1.
A hollow metal surface of radius 5 cm is charged, so that the potential on its surface is 10 V. The potential at the centre of the sphere is [1]
(a) 0 V
(b) 10 V
(c) same as at point 5 cm away from the surface
(d) same as at point 25 cm away from the surface
Answer:
(b) 10 V
Since, potential inside the hollow sphere is same as that on the surface,
∴ V
Centre
= 10 V
Question 2.
In the figure given below, two charges +5μC and -5μC are kept at 10 mm apart. The electric field at point P, on the axis of the dipole, 10 cm away from its centre O on the side of positive charge is [1]
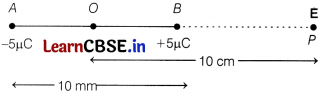
(a) 3 × 10
5
N/C
(b) 8 × 10
5
N/C
(c) 9 × 10
5
N/C
(d) 4 × 10
5
N/C
Answer:
(c) 9 × 10
5
N/C
Given, q = ± 5μC = ± 5 × 10
-6
C
2a = 10 mm = 10 × 10
-3
m
r = 10 cm = 10 × 10
-2
m
∴ |p| =|q| × 2a = 5 × 10
-6
× 10 × 10
-6
= 5 × 10
-8
C-m
The electric field along BP will be
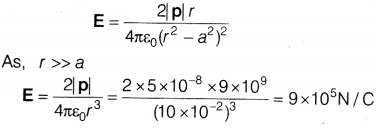
Question 3.
In photoelectric effect, if the intensity of light is doubled, then the change in maximum kinetic energy of photoelectrons versus intensity graph is correctly shown in [1]
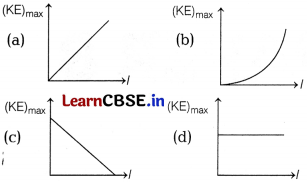
Answer:
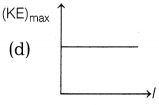
The maximum kinetic energy of emitted photoelectrons depends on the frequency of • incident radiation and nature of the material of plate, but is independent of the intensity of light.
So, it will remain unchanged which is correctly shown in option (d).
Question 4.
On bombarding U
235
by slow neutron, 200 MeV energy is released. If the output power of atomic reactor is 1.6 MW, then the rate of fission is [1]
(a) 2 × 10
12
s
-1
(b) 2.5 × 10
16
s
-1
(c) 4.2 × 10
15
s
-1
(d) 5 × 10
16
s
-1
Answer:
(d) 5 × 10
16
s
-1
Energy released on bombarding U
235
by neutron
= 200 MeV
Power output of atomic reactor, P = 1.6 MW
We know that, P = \(\frac{n E}{t}\)
(where n = total number of fissions)
⇒ Rate of fission = \(\frac{n}{t}\) = \(\frac{T}{E}\)
Rate of fission = \(\frac{1.6 \times 10^6}{200 \times 10^6 \times 1.6 \times 10^{-19}}\)
= 5 × 10
16
s
-1
Question 5.
Ampere circuital law is given by [1]
(a) \(\oint \mathbf{H} \cdot d \mathbf{l}=\mu_0 i_{\text {enc }}\)
(b) \(\oint \mathbf{B} \cdot d \mathbf{l}=\mu_0 i_{\text {enc }}\)
(c) \(\oint \mathbf{B} \cdot d \mathbf{l}=\mu_0 I\)
(d) \(\oint \mathbf{H} \cdot d \mathbf{l}=\mu_0 I\)
Answer:
(b) \(\oint \mathbf{B} \cdot d \mathbf{l}=\mu_0 i_{\text {enc }}\)
According to Ampere’s circuital law, magnetic flux linked to a closed current loop, is given by
\(\oint \mathbf{B} \cdot d \mathbf{l}=\mu_0 i_{\text {enc }}\)
Question 6.
Which of the following has a low value in ferrites? [1]
(a) Conductivity
(b) Permeability
(c) Magnetic susceptibility
(d) All of the above
Answer:
(a) Conductivity
Ferrites are a type of cermamic material composed primarily of iron oxide (FeO) or iron oxide combined with other metal oxides. The crystal structure of highly ionic and electrons are tightly bound. Therefore, ferrites have low conductivity.
Question 7.
In the electric field of a point charge q, a certain charge is carried from point A to B, C, D and E. Then, the work done m
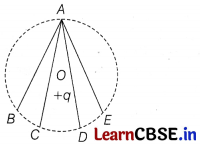
(a) is least along the path AB
(b) is least along the path AD
(c) is zero along all the paths AB, AC, AD and AE
(d) is least along AE
Answer:
(c) is zero along all the paths AB, AC, AD and AE
A, 6, C, D and E all lie on equipotential surface because on the surface of a sphere due to point charge, potential is same. So,
W
AB
= W
AC
= W
AD
= W
AE
= q(V
f
-V
i
) = zero.
Question 8.
There are two long co-axial solenoids of same length l. The inner and outer coils have radii r
1
and r
2
and number of turns per unit length n
1
and n
2
, respectively. The ratio of mutual inductance to the self-inductance of the inner coil is [1]
(a) \(\frac{n_2}{n_1}\) • \(\frac{r_1}{r_2}\)
(b) \(\frac{n_2}{n_1}\) • \(\frac{r_2^2}{r_1^2}\)
(c) \(\frac{n_2}{n_1}\)
(d) \(\frac{n_1}{n_2}\)
Answer:
(c) \(\frac{n_2}{n_1}\)
Mutual inductance for a co-axial solenoid of radius r
1
and r
2
and number of turns n
1
and n
2
, respectively is given as
M = \(\mu_0 n_1 n_2 \pi r_1^2 I\) (for inner coil of radius r,)
Self-inductance for the inner coil, L = \(\mu_0 n_1^2 \pi r_1^2 I\)
\(\frac{M}{L}\) = \(\frac{n_1 n_2}{n_1^2}\) = \(\frac{n_2}{n_1}\)
Question 9.
What is not possible in a transformer? [1]
(a) Alternating current
(b) Eddy current
(c) Direct current
(d) Induced current
Answer:
(c) Direct current
Transformer is used to convert the value of AC voltage. It works on the principle of electromagnetic induction. So, direct current is not possible in it.
Question 10.
Radiations of intensity 0.5 Wm
-2
are striking a metal plate. The pressure on the plate is [1]
(a) 0.166 × 10
-8
Nm
-2
(b) 0.332 × 10
-8
Nm
-2
(c) 0.111 × 10
-8
Nm
-2
(d) 0.083 × 10
-8
Nm
-2
Answer:
(b) 0.332 × 10
-8
Nm
-2
As metal is a reflecting surface, so for a reflecting surface radiation pressure,
P
r
= \(\frac{2 S}{c}\) = \(\frac{2 \times 0.5}{3 \times 10^8}\) = 0.332 × 10
-8
Nm
-2
Question 11.
According to Faraday’s law of electromagnetic induction, [1]
(a) electric field is produced by time varying magnetic flux
(b) magnetic field is produced by time varying electric flux
(c) magnetic field is associated with a moving charge
(d) None of the above
Answer:
(a) electric field is produced by time varying magnetic flux
Faraday’s law states that time varying magnetic flux can induce an emf.
Question 12.
In Bohr’s model, the atomic radius of the first orbit is r
0
. Then, the radius of the third orbit is [1]
(a) \(\frac{r_0}{a}\)
(b) r
0
(c) 9 r
0
(d) 3 r
0
Answer:
(c) 9 r
0
The radius of nth orbit is given by
r
n
= r
0
× n²
r
3
= 9 r
0
For questions 13 to 16 two statements are given-one labelled
Assertion (A) and other labelled Reason (R).
Select the correct answer to these questions from the options as given below.
(a) If both A and R are true and R is the correct explanation of A.
(b) If both A and R are true but R is not the correct explanation of A.
(c) If A is true but R is false.
(d) If both A and R are false.
Question 13.
Assertion (A) Photosensitivity of a metal is high, if its work function is small.
Reason (R) Work function =hf
0
, where f
0
is the threshold frequency. [1]
Answer:
(b) If both A and R are true but R is not the correct explanation of A.
Less work function means less energy is required for ejecting out the electrons.
Question 14.
Assertion (A) A pure semiconductor has negative temperature coefficient of resistance.
Reason (R) In a semiconductor on raising the temperature more charge carrier are released, conductance increases and resistance decreases. [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
In semiconductor, by increasing temperature covalent bond breaks and conduction hole and electrons increase.
Question 15.
Assertion (A) An emf can be induced by moving a conductor in a magnetic field.
Reason (R) An emf can be induced by changing the magnetic field. [1]
Answer:
(a) If both A and R are true and R is the correct explanation of A.
In both the cases, the magnetic flux will change, and so there is an induced current.
Question 16.
Assertion (A) The image of a point object situated at the centre of hemispherical lens is also at the centre.
Reason (R) For hemisphere Snell’s law is not valid. [1]
Answer:
(c) If A is true but R is false.
The rays from centre of hemisphere cut at the centre after refraction, Snell’s law is valid in each case of refraction.
Section B
Question 17.
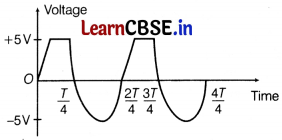
Assuming an ideal diode, draw the output waveform for the circuit given in the figure, explain the waveform. [2]
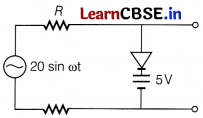
Answer:
In a rectifier circuit with output of 5V battery.
In forward biased, for input voltage greater than 5V will appear across resistor R and hence i did not waveforms at 5V is obtained.
When input voltage is negative. The input waveform is then passed on to the output terminals, so max
V
output
= -5V.
The output waveform is shown here in the figure
Question 18.
There are materials which absorb photons of shorter wavelength and emit photons of longer wavelength. Can there be stable substances which absorb photons of larger wavelength and emit light of shorter wavelength? [2]
Answer:
According to first statement, when the materials which absorb photons of shorter wavelength has high energy of the incident photon on the material and low energy of emitted photon of longer wavelength.
But in second statement, the energy of the incident photon is low for the substances which has to absorb photons of larger wavelength and energy of emitted photon is high to emit light of shorter wavelength. This means in this statement material has to supply the energy for the emission of photons. But this is not possible for a stable substances.
Question 19.
(i) When monochromatic light travels from a rarer to a denser medium, explain the following, giving reasons.
(a) Is the frequency of reflected and refracted light same as the frequency of incident light?
(b) Does the decrease in speed imply a reduction in the energy carried by light wave? [1]
(ii) Mention any two situations in which Snell’s law of refraction fails. [1]
Answer:
(i) (a) The frequency of reflected and refracted light remains same as that of incident light because frequency only depends on the < source of light.
(b) Since, the frequency remains same, hence there is no reduction in energy.
(ii) Snell’s law of refraction fails in two situations
(a) When TIR (total internal reflection) takes place at angle greater than the critical angle.
(b) When light is incident normally on a surface, as i = 0, r = 0.
Question 20.
(i) The potential difference applied across a given resistor is altered, so that the heat produced per second increases by a factor of 9. By what factor does the applied potential difference change? [1]
(ii) A wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter? [1]
Answer:
(i) Heat produced per second = I² R = \(\frac{V^2}{R}\)
So, when voltage is made three times, then heat produced increase nine times for same R.
(ii) As shown in figure, the two resistances of value 3R each are in parallel with each other.
The above circuit can also be realised as the circuit given below
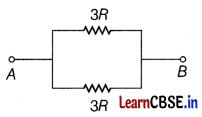
So, the effective resistance between the ends A and B of a diameter,
R’ = \(\frac{R_1 \times R_2}{R_1+R_2}\)
= \(\frac{3 R \times 3 R}{3 R+3 R}\)
= \(\frac{9 R^2}{6 R}\)
= \(\frac{3}{2}\) R
Question 21.
(i) An equiconvex lens of focal length f is cut into two equal halves in thickness. What is the focal length of each half ? [1]
(ii) A magician during a show makes a glass lens μ = 1.47 disappear in a trough of liquid. What is the refractive index of the liquid? Could the liquid be water? [1]
Or
A symmetric biconvex lens of radius of curvature R made of glass of refractive index 1.5, is placed on a layer of liquid placed on the top of a plane mirror as shown in the figure. An optical needle with its tip on the principal axis of the lens is moved along the axis until its real, inverted image coincides with the needle itself. The distance of the needle from the lens is measured to be x. On removing the liquid layer and repeating the experiment, the distance is found to be y. Obtain the expression for the refractive index of the liquid in terms of x and y. [2]
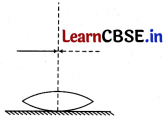
Answer:
(i) Equiconvex lens have the same radius of curvature. Therefore, the focal length will be doubled when cut from half,
i.e. f’ = 2f
(ii) If μ
1
= μ
2
, then f = ∞
Hence, the lens in the liquid acts like a plane sheet, when refractive index of the lens and the surrounding medium is the same. Therefore,
μ
1
= μ
2
= 1.47
Hence, the liquid medium is not water, refractive index for water = 1.33.
Or
First measurement gives the focal length (f
eq
= x) combination of the convex lens and the plano-convex liquid lens. Second measurement gives the focal length (f
1
= y) of the convex lens. Focal length (f
2
)of plano-convex lens is given by
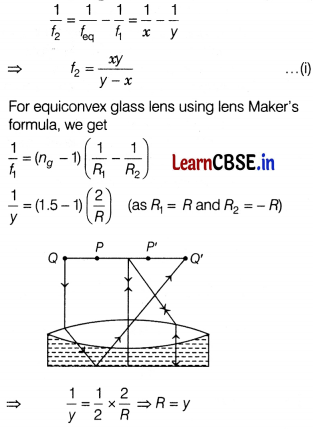
Now, we apply lens Maker’s formula for plano-convex lens.
Here R
1
= R and R
2
= ∞ and let n
i
= refractive index of liquid
Section C
Question 22.
In the study of Geiger-Marsden experiment on scattering of α -particles by a thin foil of gold, draw the trajectory of α-particles in the coulomb field of target nucleus. Explain briefly how one gets the information on the size of the nucleus from this study. From the relation R = R
0
A
1
, where R0 is constant and A is the mass number of the nucleus, show that nuclear matter density is independent of A. [3]
Answer:
Trajectory of α-particles in the coulomb field of target nucleus is shown below
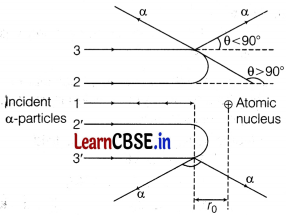
From this experiment, the following points are observed.
(i) Most of the α-particles pass straight through the gold foil. It means that they do not suffer any collision with gold atoms.
(ii) About one α-particle in every 8000 α-particles deflects by more than 90°. As most of the α-particles go undeflected and only a few get deflected, this shows that most of the space in an atom is empty and at the centre of the atom, there exists a nucleus. By the number of α-particles get deflected, the information regarding size of the nucleus can be known.
Let V be the volume of nucleus
i.e. V = \(\frac{4}{3}\) πR³
Density, ρ = \(\frac{M}{V}\)
As. we know that, M = \(\frac{4}{3}\) πR³ A ρ = mA
where, m = constant 3m
∴ ρ = \(\frac{3 m}{4 \pi R_0^3}\)
Question 23.
Two identical parallel plate capacitors A and B are connected to a battery of V volts With the switch S is closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant K. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric. [3]
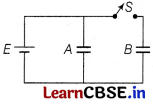
Answer:
The given figure is shown below
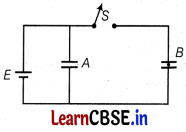
When switch S is closed, the potential difference across capacitors A and B are same.
i.e., V = \(\frac{Q_A}{C}\) = \(\frac{Q_B}{C}\)
Initial charges on capacitors
Q
A
= Q
B
= CV
When the dielectric is introduced, the new capacitance of either capacitor
C’ = KC
As switch S is opened, the potential difference across capacitor A remains same (V volts).
Let potential difference across capacitor BbeV’. When dielectric is introduced with switch S open (i.e. battery disconnected), the charges on capacitor B remains unchanged, so
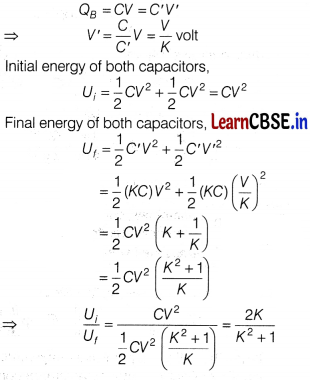
Question 24.
(i) State Bohr’s postulate to define stable orbits in hydrogen atom. How does de-Broglie’s hypothesis explain the stability of these orbits? [2]
(ii) A hydrogen atom initially in the ground state absorbs a photon which excites it to the n = 4 level. Estimate the frequency of the photon. [1]
Answer:
(i) Bohr’s second postulate defines the stable orbits, This postulate states that the electron revolves around the nucleus only in those orbits for which the angular momentum is some integral multiple of h/2π, where h is the Planck’s constant (= 6.63 x10-34 J-s)
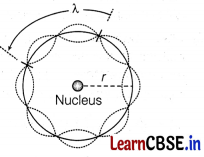
According to de-Broglie, wavelength of moving electron, λ = \(\frac{h}{m v_n}\)
where, v
n
is speed of electron revolving in nth orbit.
As, 2πr
n
= nX
2πr
n
= \(\frac{nh}{m v_n}\) or mv
n
r
n
= \(\frac{n h}{2 \pi}\) = n(h/2π)
i.e. Angular momentum of electron revolving in nth orbit must be an integral multiple of h/2π, which is the quantum condition proposed by Bohr in his second postulate.
(ii) We know that, energy of electron in nth orbit is

Question 25.
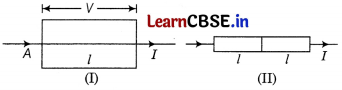
(i) A metal rod of square cross-sectional area A having length l has current I flowing through it when a potential difference of V volt is applied across its ends (Fig. I). Now, the rod is cut parallel to its length into two identical pieces and joined as shown in Fig. II. What potential difference must be maintained across the length of 2l, so that the current in the rod is still I ? [1]
(ii) A conductor of length l is connected to a DC source of potential V. If the length of the conductor is tripled by gradually stretching it, keeping V constant, how will
(a) drift speed of electrons and
(b) resistance of the conductor be affected? Justify your answer. [2]
Answer:
(i) From Ohm’s law, we have V = IR
V = Iρ\(\frac{l}{A}\) [∵ R = \(\rho \frac{l}{A}\)]
When the rod is cut parallel and rejoined by length, the length of the conductor becomes 2l, whereas the area decrease to A/2. If the current remains the same, then the potential changes as
V = Iρ\(\frac{2 l}{A/2}\) = 4 × Iρ\(\frac{l}{A}\) = 4 V [using Eq. (i)]
The new potential applied across the metal rod will be four times the original potential (V).
(ii) When a wire is stretched, then there is no change in the matter of the wire, hence its volume remains constant.
The potential V = constant, l’ = 3l
(a) Drift speed of electrons = \(\frac{V}{\text { nelp }}\)
∴ v ∝ \(\frac{1}{l}\) [∵ other factors are constants]
So, when length is tripled, drift velocity gets one-third.
(b) Here, volume remains same V
1
= V
1
∴ A
1
l
1
= A
2
l
2
A
1
l
1
= A
2
(3l)
⇒ [∵ length is tripled after stretching]
∴ A
2
= \(\frac{A_1}{3}\)
i.e. When length is tripled area of cross-section is reduced to \(\frac{A}{3}\).
Hence, R = ρ\(\frac{l’}{A’}\) = ρ\(\frac{3 l}{\frac{A}{3}}\)= 9 ρ\(\frac{l}{A}\) = 9R
Thus, new resistance will be 9 times of its original value.
Question 26.
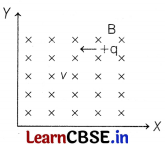
(i) A point charge is moving with a constant velocity perpendicular to a uniform magnetic field as shown in the figure. What should be magnitude and direction of the electric field, so that the particle moves undeviated along the same path? [2]
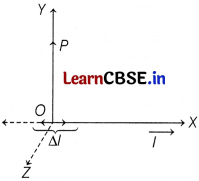
(ii) An element ∆l = ∆x \(\hat{i}\) is placed at the origin (as shown in figure) and carries a current I = 2 A. Find out the magnetic field at a point P on the F-axis at a distance of 1.0 m due to the element ∆x = w m. Also, give the direction of the field produced. [1]
Answer:
(i) As, v = -v \(\hat{i}\)
[∵ the particle is moving along x-direction]
B = – B \(\hat{k}\)
[∵ the magnetic field is perpendicular to the plane of the paper directed inwards, i.e. negative z-direction]
∴ Force acting due to magnetic field,
F
m
=q (v × B)
= q [- v \(\hat{i}\) × (- B \(\hat{k}\))],
F
m
= -qvB\(\hat{j}\) [∵ \(\hat{i}\) × \(\hat{k}\) = – \(\hat{j}\)]
⇒ Magnitude of F
m
= | F
m
| = qvB
The direction of F
m
is along negative Y-direction.For the undeflected motion of particle,
Force due to electric field = Force due to magnetic field,
qE = q(v × B)
∴ E = v × B
Magnitude of electric field, |E| = |v × B| and direction of electric field will be perpendicular to both v and B, i.e. along Y-axis.
(ii) Biot-Savart’s law states that
dB = \(\frac{\mu_0}{4 \pi}\) . \(\frac{\mid d \mathbf{l} \times \hat{\mathbf{r}}}{|\mathbf{r}|^2}\)
Here, ∆x = w m
v ∆l = x \(\hat{i}\)
⇒ l = 2A, r = 1 m
dB = \(\frac{\mu_0}{4 \pi}\) . \(\frac{(2 w \hat{\mathbf{i}} \times \hat{\mathbf{j}})}{(1)^2}\)
Idl = 2 × w \(\hat{i}\)
\(\hat{r}\) = \(\hat{j}\) ⇒ | r | = 1 m
dB = \(\frac{\mu_0 w}{2 \pi}\) \(\hat{k}\) ⇒ dB = \(\frac{\mu_0 w}{2 \pi}\)
and direction along +Z-axis.
Question 27.
Answer the following questions.
(i) Name the electromagnetic waves which are used for the treatment of certain forms of cancer. Write their frequency range. [1]
(ii) Thin ozone layer on top of stratosphere is crucial for human survival. Why?
(iii) Why is the amount of the momentum transferred by the electromagnetic waves incident on the surface so small? [1]
Answer:
(i) y-rays; Its frequency range is from 3 × 10
19
to 3 × 10
23
Hz.
(ii) The thin ozone layer on top of stratosphere absorbs most of the harmful ultraviolet rays coming from the sun towards the earth. They include UVA, UVB and UVC radiations which can destroy the life system on the earth. Hence, this layer is crucial for human survival.
(iii) Momentum transferred = Energy/Speed of light
= \(\frac{E}{c}\) = \(\frac{hv}{c}\) ≈ 10
-22
Thus, the amount of the momentum transferred by the electromagnetic waves incident on the surface is very small.
Question 28.
State the principle of an AC generator. Obtain the expression for the emf induced in a coil having N turns each of cross-sectional area A, rotating with a constant angular speed 00 in a magnetic field B, directed perpendicular to the axis of rotation. [3]
Or
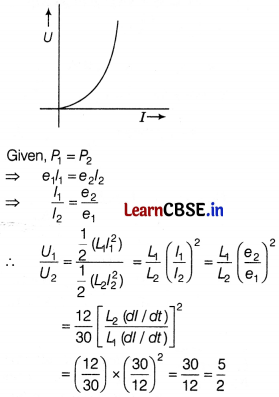
The current through two inductors of self-inductance 12 mH and 30 mH is increasing with time at the same rate. Draw graphs showing the variation of the
(i) emf induced with the rate of change of current in each inductor. [1]
(ii) energy stored in each inductor with the current flowing through it.
Compare the energy stored in the coils, if the power dissipated in the coils is the same. [2]
Answer:
Principle: An AC generator is based on the phenomenon of electromagnetic induction which states that whenever magnetic flux linked with a conductor (or coil) changes, an emf is induced in the coil.
Magnetic flux linked with the coil is given by
ϕ = A/ (B • A) or ϕ = NBA cos θ
ϕ = NBA cos ωt
where, ω is angular velocity of the coil and symbols have usual meaning.
As we know, due to the rotation of the coil, an emf is being induced.
Thus, at this instant t, ife is the emf induced in the coil, then
e = –\(\frac{d \phi}{d t}\)
e = – \(\frac{d}{d t}\) (NAB cos ωt)
e = – NAB \(\frac{d}{d t}\)(cos ωt)
e = – NAB (- sin ωt) = NAB sin ωt
where, NBA ω is the maximum value of the emf (also called peak value) which occurs when sin ωt = ±1.
If NBA e = e
0
, then e = e
0
sin ωt.
Or
Given, L
1
= 12 mH, L
2
= 30 mH
Also, \(\frac{d l_1}{d t}\) = \(\frac{d l_2}{d t}\)
(i) Induced emf in the inductors,
|e| = L\(\frac{d l}{d t}\)
Thus, graph of e versus \(\frac{d l}{d t}\) for two inductors is as shown in figure.
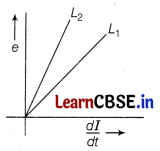
∵ L
1
> L
2
∴ For the given \(\frac{d l}{d t}\), e
2
> e
1
.
(ii)
Section D
[Case Study Based Questions]
Question 29.
Read the following paragraph and answer the questions that follow.
A ray PQ is incident on face AB. As it enters the denser medium (glass), it bends towards the normal along path QR. The ray QR suffers another refraction at face AC, bending away from the normal, it emerges along RS.
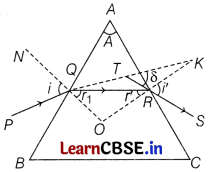
So, angle of incidence + angle of emergence = angle of prism + angle of
deviation
δ = i + i’ – A or i + i’= A + δ
From Snell’s law,
μ = \(\frac{\sin i}{\sin r}\) ⇒ μ = \(\frac{\sin \left(\frac{A+\delta_m}{2}\right)}{2}\)
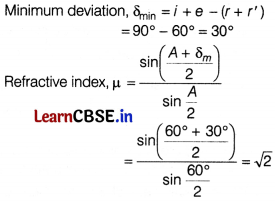
(i) The angle of incidence for a ray of light at a refracting surface of prism is 45°. The angle of emergence is 45°. The angle of prism 60°. If the ray suffers minimum deviation through the prism, then angle of minimum deviation and refractive index of prism is [1]
(a) 30°, √2
(b) 45, √2
(c) 30°, \(\frac{1}{\sqrt{2}}\)
(d) 45°, \(\frac{1}{\sqrt{2}}\)
Answer:
(a) 30°, √2
Given i = 45°
r = r’ = 30°
i’ = e = 45°
Angle of prism, A = 60°
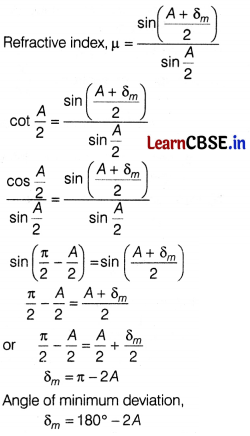
(ii) The refracting angle of a prism is A and refractive index of the material of the prism is cot (A/2). The angle of minimum deviation is [1]
(a) 180° – 3A
(b) 180°- 2A
(c) 90°- A
(d) 180° + 2A
Answer:
(b) 180°- 2A
(iii) Angle of minimum deviation for a prism of refractive index 1.5 is equal to the angle of prism of given prism. The angle of prism is [1]
(a) 80°
(b) 41°24′
(c) 60°
(d) 82°48′
Answer:
(d) 82°48′
Given, μ = 1.5
Refractive index
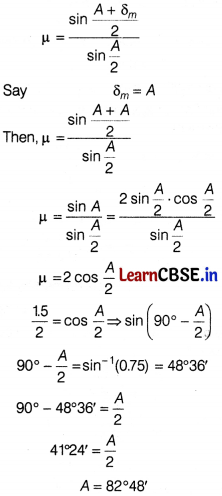
Or
A ray of light passes from medium A having refractive index 1.6 to the medium B having refractive index 1.5. The value of critical angle of medium A is [1]
(a) \(\sin ^{-1} \sqrt{\frac{16}{15}}\)
(b) \(\sin ^{-1}\left(\frac{16}{15}\right)\)
(c) \(\sin ^{-1}\left(\frac{1}{2}\right)\)
(d) \(\sin ^{-1}\left(\frac{15}{16}\right)\)
Answer:
(d) \(\sin ^{-1}\left(\frac{15}{16}\right)\)
As the law of refractive, we have
\(\) = \(\frac{15}{16}\)
sin i
c
= \(\frac{15}{16}\)
where i
c
= critical angle of medium
i
c
= \(\sin ^{-1}\left(\frac{15}{16}\right)\)
(iv) The limiting angle of incidence for an optical ray that can be transmitted by equilateral prism of refractive index μ = \(\sqrt{\frac{7}{3}}\), is given by [1]
(a) \(\frac{\pi}{3}\)
(b) \(\frac{\pi}{6}\)
(c) \(\frac{2 \pi}{3}\)
(d) \(\frac{\pi}{2}\)
Answer:
(b) \(\frac{\pi}{6}\)
μ = \(\sqrt{\frac{7}{3}}\)
A = 60°
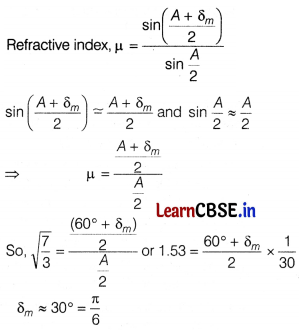
Question 30.
Read the following paragraph and answer the questions that follow.
A block of semiconductor of length l, area of cross-section A, having free electron density n
e
and hole density n
h
.
Potential difference V is applied across its ends,
E = \(\frac{V}{l}\)
Total current is equal to the sum of electron current and hole current,
i. e. I = I
e
+ I
n
and conductivity a = – = e (nepe + nh\xh) P
As temperature increase, the mobilities \i.e and p h of electrons and holes decreases due to this increase in their collisions, frequency. But due to the electron from the valence band cross over the conduction band.
(i) A p -type semiconductor has acceptor level 50 meV above the valence band. The maximum wavelength of light that can create a hole is [1]
(a) 2.47 × 10
-5
m
(b) 2.6 × 10
-6
m
(c) 2.8 × 10
-4
m
(d) 2.6 × 10
-3
m
Answer:
(a) 2.47 × 10
-5
m

(ii) An intrinsic germanium semi¬conductor is to be made n-type semiconductor of conductivity 6 mho/cm.
The number density of donor atoms required, if the mobility of electron in n-type semiconductor is 3850 cm²/Vs is [1]
(a) 9.7 × 10
21
/m
3
(b) 8 × 10
20
/m
3
(c) 6 × 10
18
/m
3
(d) 6.2 × 10
21
/m
3
Answer:
(a) 9.7 × 10
21
/m
3
n-type semiconductor, n
e
<< n
h
Let number of semiconductor is given by
N
0
= n
h
Conductivity of semiconductor, σ = n
e
× e × μ
e
Putting the values, we get
6 × 10
2
= n
e
× 1.6 × 10
-19
× 3850 × 10
-4
n
e
= 9.7 × 10
21
/m
3
(iii) If ne and nh represent the number of free electrons and holes respectively in a semiconducting material, then for n-type semiconducting material [1]
(a) n
e
<< n
h
(b) n
e
>> n
h
(c) n
e
= n
h
(d) n
e
= n
h
= 0
Answer:
(b) n
e
>> n
h
For n-type semiconductor material, number of free electron is very greater than number of holes.
(iv) Which of the following has negative temperature coefficient of resistance? [1]
(a) Copper
(b) Aluminum
(c) Iron
(d) Germanium
Answer:
(d) Germanium
Germanium has negative temperature coefficient of resistance due to germanium is semiconductor its resistance decrease with rise in temperature.
Or
On increasing the reverse bias to a large value in p-n junction diode, current [l]
(a) increases slowly
(b) remains fixed
(c) suddenly increases
(d) decreases slowly
Answer:
(c) suddenly increases
When a large reverse voltage is applied across p-n junction diode huge current flows in the reverse direction suddenly. This is breakdown of p-n junction diode.
Section E
Question 31.
(i) A point object O is kept in a medium of refractive index n
1
in front of a convex spherical surface of radius of curvature R which separates the second medium of refractive index n
2
from the first one, as shown in the figure.
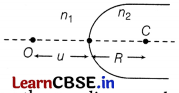
Draw the ray diagram showing the image formation and deduce the
relationship between the object distance and the image distance in terms of n
1
, n
2
and R. [3]
(ii) When the image formed above acts as a virtual object for a concave spherical surface separating the medium n
2
from n
1
(n
2
> n
1
), draw this ray diagram and write the similar [similar to (i)] relation. Hence obtain the expression for the lens Maker’s formula.
Answer:
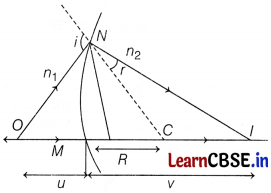
Let a spherical surface separate a rarer medium of refractive index n
1
from the second medium of refractive index n
2
. Let C be the centre of curvature and R = MC be the radius of curvature.
Consider a point object O lying on the principal axis of the surface. Let a ray starting from O incident normally on the surface along OM and pass straight. Let another ray of light incident on NM along ON and refract along Nl. From M, draw MN perpendicular to OI.
The given figure shows the geometry of the formation of image I of an object 0 and the principal axis of a spherical surface with centre of curvature C and radius of curvature R.
Here, we have to make following assumptions,
(a) the aperture of the surface is small as compared to the other distance involved.
(b) NM will be taken as nearly equal to the length of the perpendicular from the point N on the principal axis.

(ii) Now, the image I’ acts as a virtual object for the second surface that will form a real at I. As, refraction takes place from denser to rarer medium,
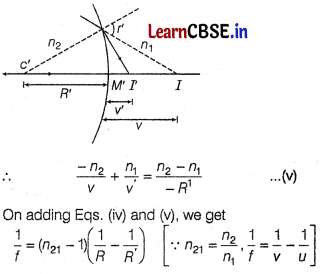
Or
(i) A small telescope has an objective lens of focal length 150 cm and eyepiece of focal length 5 cm.
What is the magnifying power of the telescope for viewing distant objects in normal adjustments?
If this telescope is used to view a 100 m tall tower 3 km away, then what is the height of the tower formed by the objective lens? [3]
(ii) You are given two converging lenses of focal length 1.25 cm and 5 cm to design a compound microscope. If it is desired to have a magnification of 30, then find out ‘the separation between the objective and eyepiece. [2]
Answer:
(i) When final image is at D, then
magnifying power, m = \(\frac{-f_0}{f_e}\) = (1 + \(\frac{f_e}{D}\))
In normal adjustment, m = \(\frac{-f_0}{f_e}\)
For telescope, focal length of objective lens, f
0
= 150 cm
Focal length of eye lens, f
e
= 5 cm
When final image forms at infinity in normal
magnification, m = \(\frac{-f_0}{f_e}\) = \(\frac{-150}{5}\)
⇒ m = – 30
Let height of final image be h cm.
⇒ tan ß = \(\frac{h}{25}\) and tan α = \(\frac{100 m}{3000 m}\) = \(\frac{1}{30}\)
where, ß = visual angle formed by final image at eye
and α = visual angle subtended by object at objective.

Negative sign indicates inverted image.
(ii) Given, f
0
= 125 cm, f
e
= +5 cm
Magnification, m = – 30, D = 25 cm
If the object is very close to the principal focus of the objective and the image formed by the objective is very close to eyepiece, then magnifying power of a microscope is given by
m = – \(\frac{L}{f_0}\) . \(\frac{D}{f_e}\)
⇒ 30 = \(\frac{L}{125}\) . \(\frac{25}{5}\)
⇒ L = \(\frac{125 \times 30 \times 5}{25 \times 100}\)
⇒ L = \(\frac{25 \times 30}{100}\) = L = \(\frac{30}{4}\)
⇒ L = 7.5 cm
This is a required separation between the objective and the eyepiece.
Question 32.
(i) A point charge is placed at the centre of spherical gaussian surface. How will the electric flux ϕ change, if
(a) the sphere is replaced by a cube of same or different volume? [1]
(b) a second charge is placed near and outside the original sphere? [1]
(c) the original charge is replaced by an electric dipole? [1]
(ii) Two point charges q
A
= 3 μC and q
B
= -3 μC are located 20 cm apart in . vacuum. What is the electric field and its direction at the mid-point O of the line AB joining the two charges? [2]
Answer:
(i) By Gauss’s law, electric flux passing through closed surface, ϕ = \(\oint E \cdot d \mathbf{S}\) = \(\frac{q}{\varepsilon_0}\)
where, q is the net charge enclosed in the gaussian surface.
(a) ϕ does not change because it depends only on the total charge enclosed by the gaussian surface and not on its shape or size.
(b) ϕ will not change because the total flux is determined by the charge inside the surface, not on the charge outside.
(c) ϕ becomes zero because a dipole consists of two equal and opposite charges and so the net charge inside the surface is zero. Thus, the flux is also zero.
(ii) Given, AB = 20 cm
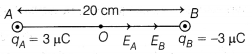
AO = OB = 10 cm = 0.1 m
q
A
= 3 μC = 3 × 10
-6
C
q
B
= -3 μC = – 3 × 10
-6
C
The electric field at a point due to a charge q,
E = \(\frac{1}{4 \pi \varepsilon_0}\) . \(\frac{q}{r^2}\)
where, r is the distance between charge and the point.
Electric field due to q
A
at O,

The direction of E
B
is O to B, i.e. towards B or towards OB as the electric field is always directed towards the negative charge.
Now, we see that both E
A
and E
B
are in same direction. So, the resultant electric field at O is E.
Hence,
E = E
A
+ E
B
= 2.7 × 10
6
+ 2.7 × 10
6/sup>
= 5.4 × 10
5
N/C
The direction of E (resultant electric field) will be from O to B or towards B.
To get maximum marks, show the Points Posit’011 of charges with suitable ’ distances in diagram.
Or
(i) A molecule of a substance has a permanent electric dipole moment of magnitude 10
-29
C-m. A mole of this substance is polarised (at low temperature) by applying a strong electrostatic field of magnitude 10
6
Vm”1. The direction of the field is suddenly changed by an angle of 60°. Calculate the heat released by the substance in aligning its dipoles along the new direction of the field. [3]
(ii) A capacitor of 2 pF is charged as shown in the figure. When the switch S is turned to position 2, then find the percentage of its stored energy dissipated. [2]
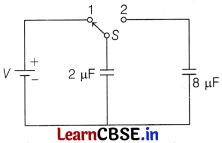
Answer:
(i) Here, the dipole moment of each molecule,
= 10
-29
C-m
1 mole of the substance contains 6 × 10
23
molecules.
Therefore, total dipole moment of all molecules,
p = 6 × 10
23
× 10
-29
C-m
= 6 × 10
-6
C-m
Initial potential energy,
U = -pE cos θ = – 6 × 10
-6
× 10
6
cos 0° = -6 J
Final potential energy (when θ = 60°),
[finally p and £ are aligned in the same direction]
L/f = – 6 × 10
-6
× 10
5
cos 60° = – 3 J
Change in potential energy
= [(- 3) – (- 6)] = 3J
So, there is a loss in potential energy. This must be the energy released by the substances in the form of heat in aligning its dipole.
(ii) Initially, energy stored in the capacitor can be
given as E = \(\frac{1}{2}\) CV²
When the switch S is connected to point 2, then energy dissipated on connecting across 8 μF will be

Question 33.
(i) When an AC source is connected to an ideal inductor, show that the average power supplied by the source over a complete cycle is zero. [1]
(ii) A lamp is connected in series with an inductor and an AC source.
What happens to the brightness of the lamp when the key is plugged in and an iron rod is inserted inside the inductor? Explain. [1]
(iii) A device X is connected to an AC source V = V
0
sin ωt. The current through X is given as,
I = I
0
sin (ωt + \(\frac{\pi}{2}\))
(a) Identify the device X and write the expression for its reactance. [1]
(b) Draw graphs showing variation of voltage and current with time over one cycle of AC, for X. [1]
(c) How does the reactance of the device X vary with frequency of the AC? Show this variation graphically. [1]
Answer:
(i) As P
av
= V
rms
I
rms
cos ϕ
In ideal inductor, current I
rms
lags behind applied voltage V
rms
by π/2.
∴ ϕ = π/2
Thus, P
av
= V
rms
I
rms
cos π/2.
= V
rms
I
rms
× 0
= 0
(ii) Brightness of the lamp decreases. It is because when iron rod is inserted inside the inductor, its inductance L increases, thereby increasing its inductive reactance X L , and hence impedance Z of the circuit. As I rms = so this decreases the current rms in the circuit and hence the brightness of lamp decrease.
(iii) (a) Given, V = V
0
sin at
I = I
0
sin (ωt + \(\frac{1\pi}{2}\))
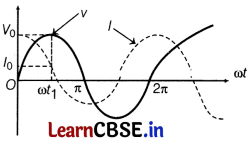
As it is clear that, the current leads the voltage by a phase angle \(\frac{\pi}{2}\).
∴ The device X is a capacitor.
The reactance of the capacitance is X
C
= \(\frac{1}{\omega C}\)
where, ω = angular frequency
and C = capacitance of capacitor
(b)
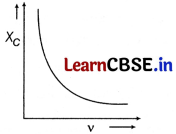
(c) The reactance of the capacitance is given as
X
C
= \(\frac{1}{\omega C}\)
where, ω = angular frequency
and C = capacitance of capacitor
∴ X
C
= \(\frac{1}{2 \pi v C}\)
where v = frequency of AC or X
C
a \(\frac{1}{v}\)
∴ The graphical representation between reactance of capacitance and frequency is given as
Or
(i) 1 MW power is to be delivered from a power station to a town 10 km away. One uses a pair of Cu wires of radius 0.5 cm for this purpose. Calculate the fraction of ohmic losses to power transmitted, if
(a) power is transmitted at 220 V. Comment on the feasibility of doing this.
(b) a step-up transformer is used to boost the voltage at 11000 V, power transmitted, then a step-up transformer is used to bring voltage is 220 V.
(Take, ρ
Cu
= 1.7 × 10
-8
SI unit) [3]
(ii) A transformer is used to step-down AC voltage. What device do you use to step-down DC voltage? [2]
Answer:
(a) The town is 10 km away, length of pair of Cu wires used, L = 20 km = 20000 m.
Resistance of Cu wires,
R = ρ \(\frac{L}{A}\) = ρ \(\frac{L}{\pi (r)^2}\)
= \(=\frac{1.7 \times 10^{-8} \times 20000}{3.14\left(0.5 \times 10^{-2}\right)^2}\) = 4Ω
I at 220 V, W = 10
6
W; I = \(\frac{10^6}{220}\) = 0.45 × 10
4
A
Power loss =RI² = 4 × (0.45)² × 10
8
> 10
6
W
Therefore, this method of transmission of power is not feasible.
(b) When power, P = 10
6
W is transmitted at 11000 V.
V’I’= 10
6
W= 11000 I’
Current drawn, I’ = \(\frac{1}{1.1}\) × 10²
Power loss,
= R(I’)² = \(\frac{1}{121}\) × 4 × 10
6
= 3.3 × 10
4
W
∴ Fraction of power loss
= \(\frac{3.3 \times 10^4}{10^6}\) = 3.3 %
(ii) An ohmic resistance can be used to step-down DC voltage, such as in potential dividing arrangement.