CBSE Sample Papers for Class 12 Maths Set 8 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 12 Maths with Solutions Set 8 are designed as per the revised syllabus.

CBSE Sample Papers for Class 12 Maths Set 8 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
If \(\vec{a}=7\hat{i}+\hat{j}-4\hat{k}\) and \(\vec{b}=2\hat{i}+6\hat{j}+3\hat{k}\), then the projection of \(\vec{a}\) on \(\vec{b}\) is
(a) \(\frac{8}{5}\)
(b) \(\frac{8}{7}\)
(c) \(\frac{7}{8}\)
(d) \(\frac{6}{5}\)
Solution:

Question 2.
The total number of functions from the set A = {1, 2, 3, 4} to.the set B = {a, b, c} is
(a) 80
(b) 81
(c) 90
(d) 50
Solution:
(b) If A and 6 are two sets having m and n elements respectively, then total number of functions from A to B is n ^m .
∴ Total number of functions from A to B
= (3) ⁴ [∵ m = 4, n = 3]
= 81

Question 3.
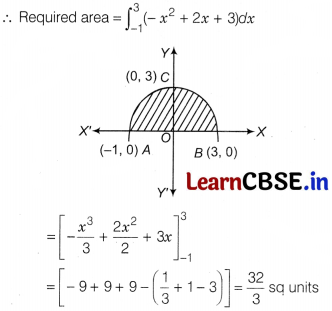
The area bounded by y = -x² + 2x + 3 and y = 0 is
(a) 32 sq units
(b) \(\frac{32}{3}\) sq units
(c) \(\frac{1}{32}\) sq units
(d) \(\frac{1}{3}\) sq units
Solution:
(b) Intersection points of given curves with X-axis are (-1, 0) and (3, 0).

Question 4.
The differential coefficient of sin (cos (x²)) with respect to x is
(a) -2xsin x² cos(cos x²)
(b) 2xsin(x²) cos(x²)
(c) 2xsin(x²) cos(x²) cos x
(d) None of the above
Solution:
(a) The function f(x) = sin[cos(x²)] is a composition
f(x) = (w o v o u)(x) of the three functions u, v and w, whereu(x) = x², v(t) = cost and w(s) = sin s.
Put f =u(x) = x2 and s = v(t) = cosf. Observe that \(\frac{dw}{ds}\) = cos s, \(\frac{ds}{dt}\) = -sin t and \(\frac{dt}{dx}\) = 2x exist for all realx.
Hence, by a generalisation of chain rule, we have

Question 5.
If a line makes angles \(\frac{\pi}{2},\frac{3\pi}{4}\) and \(\frac{\pi}{4}\) with X, Y and Z-axes respectively, then the direction cosines are

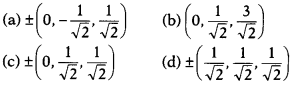
Solution:

Question 6.
The domain of the function cos ^-1 (2x -1) belongs to
(a) [0, 1]
(b) (0, 1)
(c) (0, 1]
(d) [0, 1)
Solution:
(a) We have, f(x) = cos ^-1 (2x – 1)
∴ -1 ≤ 2x – 1 ≤ 1
⇒ 0 ≤ 2x ≤ 2 ⇒ 0 ≤ x ≤ 1
∴ x ∈ [0, 1]

Question 7.
The value of tan ^-1 [2sin(2 cos ^-1 \(\frac{\sqrt3}{2}\))] is
(a) \(\frac{\pi}{3}\)
(b) \(\frac{2\pi}{3}\)
(c) –\(\frac{\pi}{3}\)
(d) \(\frac{\pi}{6}\)
Solution:

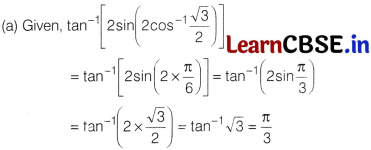
Question 8.
The relation R on the set A = {1, 2, 3} given by = {(1, 2), (2, 1)} is
(a) reflexive
(b) not reflexive
(c) not symmetric
(d) None of these
Solution:
(b) We have (1, 1), (2, 2), (3, 3) ∉ R
So, R is not reflexive.

Question 9.
The value of the expression

Solution:

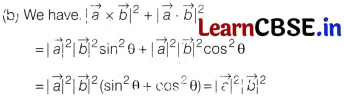
Question 10.
If A and B are two independent events such that P(A) = \(\frac{1}{3}\) and P(B) = \(\frac{1}{4}\), then P(A’ ∩ B’) equals
(a) 1
(b) \(\frac{1}{2}\)
(c) 0
(d) \(\frac{2}{3}\)
Solution:

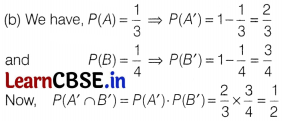
Question 11.
For the curve y = 5x – 2x³, if x increases at the rate of 2 units/s, then the rate at which the slope of curve is changing when x = 3, is
(a) -78 units/s
(b) -72 units/s
(c) -36 units/s
(d) -18 units/s
Solution:
(b) Slope of curve = \(\frac{dy}{dx}\) = 5 – 6x²
⇒ \(\frac{d}{dt}\)(\(\frac{dy}{dx}\)) = – 12x.\(\frac{dx}{dt}\)
= – 12 . (3) . (2) = – 72 units/s
Thus, slope of curve is decreasing at the rate of 72 units/s, when x is increasing at the rate of 2 units/s.

Question 12.
The function f (x) = x ⁿ , where n is a positive integer, is
(a) continuous at x = n
(b) limit of f at x = n does not exist
(c) limit of f at x = n exists and not equal to f(x)
(d) None of the above
Solution:

Thus, f(x) is continuous at x = n, where n is a positive integer.

Question 13.
Area lying in the first quadrant and bounded by the circle x² + y² = 4 and the lines x = 0 and x = 2 is
(a) π sq units
(b) \(\frac{\pi}{2}\) sq units
(c) \(\frac{\pi}{3}\) sq units
(d) \(\frac{\pi}{4}\) sq units
Solution:
(a) The area bounded by the circle and the lines x = 0 and x= 2 in the first quadrant is represented in the figure by shaded region.

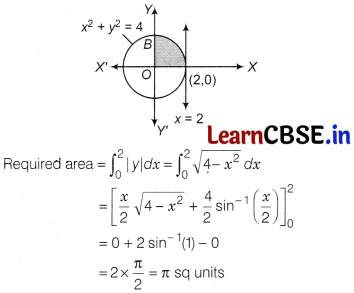
Thus, the correct option is (a).

Question 14.
Cartesian equation of the line passing through the points (1, 2, 3) and (5, 4, 6) is given by

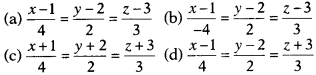
Solution:
(a) ∵ Required cartesian equation of a line passing through (1,2, 3) and (5, 4, 6) is given by

Question 15.
If the derivative of a function sec ^-1 x is \(\frac{1}{x\sqrt{x^2-1}}\), then the anti-derivative of \(\frac{1}{x\sqrt{x^2-1}}\) is
(a) sec ^-1 x
(b) sec ^-1 x + C
(c) 2 sec ^-1 x
(d) None of these
Solution:

Question 16.
Vector equation of the line

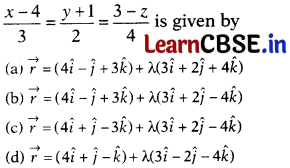
Solution:
(b) Given, equation can be re-written as
\(\frac{x-4}{3}=\frac{y-(-1)}{2}=\frac{z-3}{-4}\)
The line passes through the point (4, -1, 3) and direction ratios of the line are 3, 2, -4.
∴ Required vector equation of the given line is
\(\vec{r}=(4\hat{i}-\hat{j}+3\hat{k})+\lambda(3\hat{i}+2\hat{j}-4\hat{k})\)

Question 17.
The area of a parallelogram whose adjacent sides are represented by the

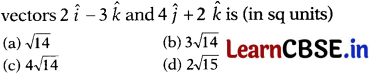
Solution:
(c) Let adjacent sides of a parallelogram be
\(\vec{a}=2\hat{i}-3\hat{k}\) and \(\vec{b}=4\hat{j}+2\hat{k}\).

Question 18.
The degree of the equation
(a) 2
(b) 0
(c) not defined
(d) 1
Solution:
(c) The given differential equation is
e ^x \(\frac{d^2y}{dx^2}\) + sin(\(\frac{dy}{dx}\)) = 3
Since, this differential equation is not a polynomial in terms of its derivatives.
∴ Its degree is not defined.

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.
Assertion (A) The f : R → R given by f(x) = [x] + x is one-one onto.
Reason (R) A function is said to be one-one and onto, if each element has unique image and range of f(x) is equal to codomain of f(x).
Solution:
(d) Assertion Since, greatest integer [x] gives only integer value.
But f(x) = [x]+ x gives all real values and there is no repeated value of f(x) for any value of x.
∴ f(x) is one-one.
f(x) = [x] + x = [x] + [x] + 2xy
f(x) = 2[x] + {x} [∵ x = [x] + 2xy]
∴ Range is (0, 1) ∪ [2, 3] ∪ [4, 5], …
∴ f(x) is not onto.
Hence, Assertion is false but Reason is true.

Question 20.
Assertion (A) cosec ^-1 is define as a function whose domain is R -(-1, 1) and range could be any

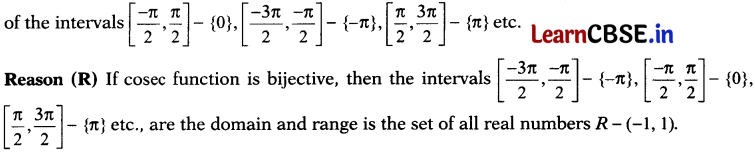
Solution:
(a) If we restrict the domain of cosec function to

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Find the value of ∫sin x.log cos x dx.
Or
Find ∫\(\frac{3-5sin x}{cos^2x}\)dx.
Solution:
∫sin x.log cos x dx
Put cos x = f ⇒ -sin x dx = dt
∴ -∫log t dt ⇒ -∫(log t).1 df

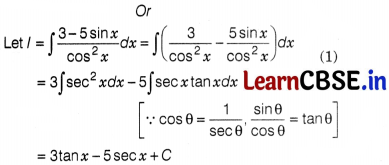
Question 22.
Show that the function f(x) = 4x³ – 18x² + 27x – 7 is always increasing on R.
Solution:
We have, f(x) = 4x³ – 18x² + 27x – 7
On differentiating both sides w.r.t. x, we get
f'(x) = 12x² – 36x + 27
⇒ f'(x) = 3(4x² – 12x + 9)
⇒ f'(x) = 3(2x – 3)²
⇒ f'(x) ≥ 0
⇒ For any x ∈ R, (2x – 3)² ≥ 0
Since, a perfect square number cannot be negative.
∴ Given, function f(x).is an increasing function on R.

Question 23.
Check if the relation R in the set A of real numbers defined as R = {(a, b): a < b} is
(i) symmetric
(ii) transitive.
Or
Check whether the relation R defined on
the set A = {1, 2, 3, 4, 5, 6} as
R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.
Solution:
Given, A = Set of real numbers and R – {(a, b):a < b}
(i) Symmetric Let (a, b) ∈ R, then a < b but b < a
⇒ (b, a) ∉ R.
e.g. 4< 5 but 5 < 4
So, R is not symmetric.
(ii) Transitive Let (a, b),(b, c) ∈ R, then
(a, b) ∈ R ⇒ a < b …(i)
(b, c) ∈ R ⇒ b < c …(ii)
From Eqs. (i) and (ii), we get a < c
⇒ (a, c) ∈ R
So, R is transitive.
Or
The relation R on set A = {1,2, 3, 4, 5, 6} is defined as (a, b) ∈ R iff b = a + 1.
Therefore, R = {(1,2), (2, 3), (3, 4), (4, 5), (5, 6)}
Clearly, (a, a) ∉ R for any a ∈ A. So, R is not reflexive on A.
We observe that (1, 2) ∈ R but (2, 1) ∉ R.
So, R is not symmetric.
We also observe that (1, 2) ∈ R and (2, 3) ∈ R but (1, 3) ∉ ft. So, it is not transitive.

Question 24.
If a line makes angles α, β and γ with the coordinate axes, then prove that
cos 2α +cos2β + cos2γ = -1.
Solution:
We know that a line makes angles a, (5 and y with the coordinate axes, then
cos²α + cos²β + cos²γ = 1
Now, cos2α + cos2β + cos2γ
= 2cos²α – 1 + 2cos²β – 1 + 2cos²γ – 1 [∵ cos2θ = 2cos²θ – 1]
= 2(cos²α + cos²β + cos²γ) – 3
= 2(1) – 3 = 2 – 3 = -1
= RHS
Hence proved.

Question 25.
Find the order and degree of the differential equation

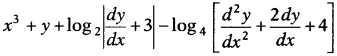
Solution:
The given differential equation is

Hence, its order is 2 and degree is 1.

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
A coin is biased so that the head is three times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails. Hence, find the mean of the number of tails.
Or
Suppose that 5 men out of 100 and 25 women out of 1000 are good orators. Assuming that there are equal number of men and women, find the probability of choosing a good orator.
Solution:
Let X be the random variable which denotes the
number of tails when a biased coin is tossed twice.
So, X may have values 0, 1 or 2.
Since, the coin is biased in which head is 3 times as likely to occur as a tail.


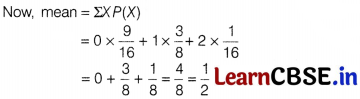
Or
Let E ₁ be the event that selected person is men and E ₂ be the event that selected person is women, E ₁ , and E ₂ are mutually exclusive and exhaustive event moreover P(E ₁ ) = P(E ₂ ) = \(\frac{1}{2}\).
Let E be the event that selected person is good orator.

Question 27.
The distance between the lines

Solution:

Question 28.
If the vertices A, B and C of a ∆ABC are (1, 2, 3), (-1,0,0) and (0, 1, 2) respectively, then find ∠ABC. (∠ABC is the angle
between the vectors \(\vec{BA}\) and \(\vec{BC}\))
Or
If \(\vec{a}=3\hat{i}+2\hat{j}+2\hat{k}\) and \(\vec{b}=\hat{i}+2\hat{j}-2\hat{k}\), then find the unit vector perpendicular to each of the vector a + b and a – b.
Solution:
The given points are A(1,2, 3), B(-1, 0, 0)andC(0,1,2).
Also, it is given that ∠ABC is the angle between the

Question 29.

Solution:

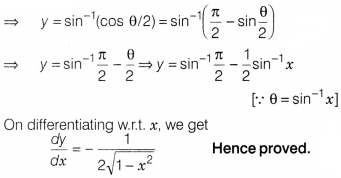
Question 30.
Find the intervals in which the function f(x) = (x – 1)³ (x – 2)² is
(i) increasing.
(ii) decreasing.
Solution:
Given, f(x) = (x – 1)³ (x – 2)²
On differentiating both sides w.r.t. x, we get

Now, we find intervals and check in which interval f(x) is strictly increasing and strictly decreasing.

Interval	f(x) = (x – 1)²(x – 2)(5x – 8)	Sign of f'(x)
x < 1	(+)(-)(-)	+ve
1 < x < \(\frac{8}{5}\)	(+)(-)(-)	+ve
\(\frac{8}{5}\) < x < 2	(+)(-)(+)	-ve
x > 2	(+)(+)(+)	+ve

We know that a function f(x) is said to be an strictly increasing function, if f'(x) > O and strictly decreasing, if f'(x) < 0.
So, the given function f{x) is increasing on the intervals (-∞, 1), (1, \(\frac{8}{5}\)) and (2, ∞) and decreasing on (\(\frac{8}{5}\), 2).
Since, f(x)is a polynomial function, so it is continuous at x = 1, \(\frac{8}{5}\), 2.
Hence, f(x) is
(i) increasing on intervals (-∞, \(\frac{8}{5}\)] and [2, ∞),
(ii) decreasing on interval [\(\frac{8}{5}\), 2].

Question 31.
Determine the area of the region bounded by the curve y² = x and the lines x = 1, x = 4 and the X-axis.
Solution:
The area of the region bounded by the curve y² = x, the lines x = 1 and x = 4 and the X-axis is shown in the figure.
Here, a = 1, b = 4

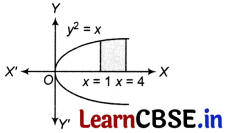
Since, the given curve y² = x is parabola which is symmetrical about X-axis (as it contains even power of y) and passes through the origin.

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.

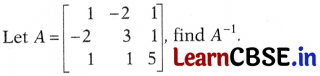
Solution:

Question 33.
Evaluate ∫\(\frac{1}{cos^4x+sin^4x}\)dx.
Solution:

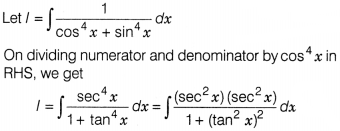
Question 34.
Solve the following LPP graphically Minimize Z = 5x + 10y,
Subject to the constraints
x +2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0 and x, y ≥ 0
Or
Solve the following LPP graphically 1 Maximize and minimize Z =3x + 5y
Subject to the constraints
3x – 4y + 12 ≥ 0,
2x – y + 2 ≥ 0,
2x + 3y – 12 ≥ 0,
o ≤ x ≤ 4,
and y ≥ 2
Solution:
Our problem is to minimize
Z = 5x + 10 y … (i)
Subject to the constraints
x + 2y ≤ 120 ,..(ii)
x + y ≥ 60 …(iii)
x – 2y ≥ 0 … (iv)
and x, y ≥ 0
Table for line x + 2y = 120 is

x	0	120
y	60	0

Put (0, 0) in the inequality x + 2y ≤ 120, we get
0 + 2 x 0 ≤ 120
⇒ 0 ≤ 120 (which is true)
So, the half plane is towards the origin.
Table for line x + y = 60 is

x	0	60
y	60	0

On putting (0, 0) in the inequality x + y ≥ 60, we get
0 + 0 ≥ 60 ⇒ 0 ≥ 60 (which is false)
So, the half plane is away from the origin.
Table for line x ~2y = 0 is

x	0	10
y	0	5

On putting (5, 0) in the inequality x – 2y ≥ 0, we get
5 -2 x 0 ≥ 0
⇒ 5 ≥ 0 (which is true)
Thus, the half plane is towards the X-axis,
Since, x, y ≥ 0
∴ The feasible region lies in the first quadrant.

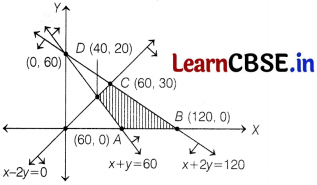
Clearly, feasible region is ABCDA.
On solving equations x – 2y = 0 and x + y = 60, we get D(40,20)and on solving equations x – 2y = Oand x + 2y = 120, we get C (60, 30). The corner points of the feasible region are A (60, 0), 6 (120, 0), C (60, 30) and D (40, 20).
The values of Z at these points are as follows

Corner points	Value of Z =5x + 10y
A(60, 0)	300 (Minimum)
B(120, 0)	600
C(60, 30)	600
D(40, 20)	400

Clearly, the minimum value of Z is 300 at the point (60,0).
Or
The given LPP can be rewritten as
Maximize or minimize Z = 3x + 5y
Subject to the constraints
3x – 4y ≥ -12 …(i)
2x – y ≥ -2 …(ii)
2x + 3y ≥ 12 …(iii)
x ≤ 4 …(iv)
y ≥ 2 … (v)
and x ≥ 0 …(vi)

Converting the inequations into equations, we obtain the following equations 3x – 4y = -12,
2x – y = -2, 2x+ 3y = 12, x = 4, y = 2 and x = 0.
Table for line 3x – 4y = -12 is

x	0	-4
y	3	0

So, line passes through the points (0, 3) and (-4, 0). On putting (0, 0) in the inequality 3x – 4y ≥ -12, we get
3 × 0 – 4 × 0 ≥ -12
⇒ 0 ≥ -12 (which is true)
So, the half plane is towards the origin.
Table for line 2x – y = -2 is

x	0	-1
y	2	0

So,line passes through the points (0, 2) and (-1, 0).
On putting (0,0) in the inequality 2x – y ≥ -2, we get
2 × 0 – 0 ≥ -2
⇒ 0 ≥ -2 (which is true)
So, the half plane is towards the origin.
Table for line 2x + 3y = 12 is

x	0	6
y	4	0

So, the line passes through the points (0, 4) and (6, 0).
On putting (0,0) in the inequality 2x + 3y ≥ 12, we get
2 × 0 + 3 × 0 ≥ 12
⇒ 0 ≥ 12 (which is false)
So, the half plane is away from the origin.
Draw the graph of the lines x = 4 and y = 2, which is perpendicular to X and Y-axes.
Putting (0, 0) in the inequality x ≤ 4, we get
0 ≤ 4 (which is true)
So,the half plane is towards the origin.
Putting (0, 0) in the inequality y ≥ 2, we get
0 ≥ 2 (which is false)
So,the half plane is away from the origin.
The shaded region P ₁ , P ₂ , P ₃ , P ₄ , P ₅ shown in figure represents the feasible region of the given LPP.
The corner points of the feasible region are P ₁ (3, 2),

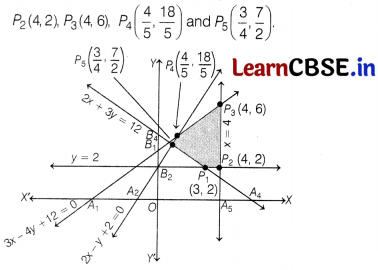
The value of the objective function at these points are given in the following table

Clearly, Z assumes its minimum value 19 at x = 3and y = 2. The maximum value of Z is 42 at x = 4 and y = 6.

Question 35.
The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By adding first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method.
Solution:
Let the first, second and third number be x, y and 2; respectively. Then, according to given conditions, we
have x + y + z = 6, y + 3z = 11
and x + z = 2y or x – 2y + z = 0
This system of equation can be written in matrix form as


Proof We shall prove this statement by using principle of mathematical induction.
Now, let P(n) be the given statement,


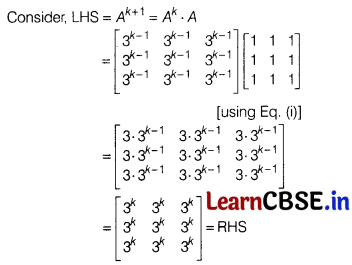
Statement is true for n = k + 1.
Hence, by principle of mathematical induction, statement is true for all n, where n ∈ N.

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
In a school, teacher asks a question to three students Ravi, Mohit, Sonia.

The probability of solving the question by Ravi, Mohit, Sonia are 30%, 25% and 45%, respectively. The probability of making error by Ravi, Mohit and Sonia are 1%, 1.2% and 2%, respectively.
On the basis of above information, answer the following questions.
(i) Find the conditional probability that an error is committed in solving question given that question is solved by Sonia.
(ii) Find the probability that Sonia solved the question and committed an error.
(iii) Find the total probability of committing an error in solving the question.
Or
If the solution of question is checked by teacher and has some error, then find the probability that the question is not solved by Ravi.
Solution:
Let
A : The event that question has some error
E ₁ : The event that question is solved by Ravi
E ₂ : The event that question is solved by Mohit
E ₃ : The event that question is solved by Sonia
Then, we have

Question 37.
An architect designs a garden in society. The garden is in the shape rectangle inscribed in a circle of radius 10m as shown in given figure.

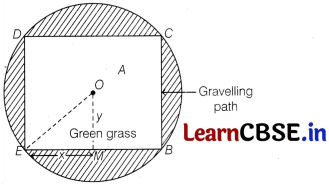
On the basis of above information, answer the following questions.
(i) If 2x and 2y represents the length and breadth of the rectangular part, then find the relation between the variables.
(ii) Find the area of the green grass A expressed as a function of x.
(iii) Show that the area A is maximum, when x = 5√2
Or
If the area A is maximum, when v = 5√2, then find the maximum area and area of gravelling path.
Solution:
(i) In ∆OEM, we have OE² = EM² + OM²
⇒ 10² = x² + y²
⇒ x² + y² = 100 …(i)
(ii) The area of green grass, A = EB × BC

The length of rectangle when A is maximum = 2x
= 2 × 5√2 = 10√2 m
⇒ y² = 100 – x² = 100 – 50 = 50 [∵ x = 5√2]
⇒ y = 5√2
⇒ 2y = 10√2m
∴ Area of rectangle = (2x)(2y) = 200 m²
Now, area of gravelling path
= Area of circle – Area of rectangle
= π(10)² – 200 = 100π – 200
= 100(π – 2)m²

Question 38.
An architect designs a building for a multi-national company. The floor consists of a rectangular region with semi-circular ends having a perimeter of 200 m as shown below

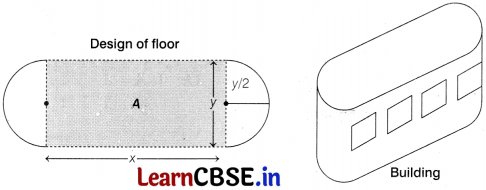
On the basis of above information, answer the following questions.
(i) Find the maximum value of area A.
(ii) The CEO of the multi-national company is interested in maximizing the area of the whole floor including the semi-circular ends. For this to happen, find the value of x.
Solution:
(i) From the figure, it is clear that perimeter of floor = 200 m
⇒ 2 × π(\(\frac{y}{2}\)) + 2x = 200
⇒ πy + 2x = 200
From figure, we have

(ii) Let B be the area of whole floor. Then,