CBSE Sample Papers for Class 12 Maths Set 2 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 12 Maths with Solutions Set 2 are designed as per the revised syllabus.

CBSE Sample Papers for Class 12 Maths Set 2 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
If \(\vec{a}\) = \(3\hat{i}+2\hat{j}+5\hat{k}\) and \(\vec{b}\) = \(6\hat{i}-\hat{j}-5\hat{k}\), then find (\(\vec{a}+\vec{b}\)) . (\(\vec{a}-\vec{b}\)).
(a) 24
(b) -24
(c) 18
(d) 10
Solution:

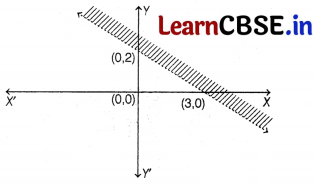
Question 2.
The graph of the inequality 2x + 3y > 6 is
(a) half plane that contains the origin
(b) half plane that neither contains the origin nor the points of the line 2x + 3y = 6
(c) whole XOF-plane excluding the points on the line 2x + 3y = 6
(d) entire A’OF-plane
Solution:
(b) The inequality 2x + 3y > 6 represent half plane that neither contains the origin nor the points of the line 2x + 3y = 6

Question 3.
If A is a square matrix of order 3, such that A(adj A) = 10I, then |adj A| is equal to
(a) 1
(b) 10
(c) 100
(d) 101
Solution:
(c) We know that,
A (adjA) = |A|l
Now, we have
A (adj A) = 10l
∴ |A| = 10
Again, |adj A | = |A| ^n-1
∴ |adj A | = |A| ^3-1 = |A|² = (10)² = 100

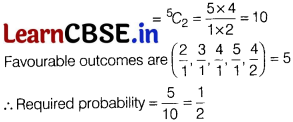
Question 4.
From the set {1,2,3,4,5}, two numbers a and b(a ≠ b) are chosen at random. The probability that \(\frac{a}{b}\) is an integer, is
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{3}{5}\)
Solution:
(c) We have, set of numbers {1,2, 3, 4, 5}.
Sample space of choosing two numbers

Question 5.
Evaluate the determinant

(a) 3
(b) 0
(c) -1
(d) 1
Solution:

Question 6.
The two lines x = ay + b, z = cy + d; and x = a’ y + b’, z = c’ y + d’ are perpendicular to each other, if

(c) aa’ + cc’ = 1
(d) aa’ + cc’ = -1
Solution:
(d) We have,
x = ay + b, z = cy + d
and x = a’y + b’, z = c’y + d’

Since, these lines are perpendicular.
∴ aa’ + 1 + cc’ = 0
[∵ two lines are perpendicular, if a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 0]
⇒ aa’ + cc’ = -1

Question 7.
If A is a 3 × 3 matrix such that |A| = 8, then |3A| equals
(a) 8
(b) 24
(c) 72
(d) 216
Solution:
(d) ∵ |KA| = K ⁿ |A|
∴ |3A| = 3³|A| [∵ n = 3]
= 27 × 8 = 216

Question 8.
If \(\vec{a}\) is a non-zero vector, then (\(\vec{a}.\hat{i}\))\(\hat{i}\) + (\(\vec{a}.\hat{j}\))\(\hat{j}\) + (\(\vec{a}.\hat{k}\))\(\hat{k}\) equals
(a) \(\vec{a}\)
(b) 2\(\vec{a}\)
(c) 3\(\vec{a}\)
(d) \(\vec{0}\)
Solution:

Question 9.
The direction ratios of the line passing through two points (2, -4, 5) and (0, 1, -1) is
(a) (-2,-6,5)
(b) (-2,5, -6)
(c) (5, -2,-6)
(d) (-6, -2,5)
Solution:
(b) Let A(x ₁ , y ₁ , z ₁ = (2, – 4, 5)
and B(x ₂ , y ₂ , z ₂ ) = (0,1,-1)
Then, DR’s of line AS is (0-2, 1 + 4, -1 -5)
i.e. (-2, 5,-6).

Question 10.

(d) None of the above
Solution:

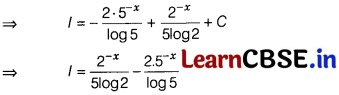
Question 11.
In an LPP, if the objective function has Z = ax + by has the same maximum value on two comer points of the feasible region, then the number of points at which Z _max occurs is
(a) 0
(b) 2
(c) finite
(d) infinite
Solution:
(d) If an objective function has the same maximum value on two comer points, then the maximum value occur at line joining two points.
∴ Infinite maximum value at line joining two points.

Question 12.
The integrating factor of the differential equation x\(\frac{dy}{dx}\) + 2y = x² is
(a) x
(b) x²
(c) 3x
(d) xy
Solution:
(b) We have, x\(\frac{dy}{dx}\) + 2y = x² ⇒ \(\frac{dy}{dx}\) + \(\frac{2}{x}\) y = x
∴ Integrating factor \(=e^{\int \frac{2}{x} d x}=e^{2 \log x}=e^{\log x^2}=x^2\)

Question 13.
If y = cos ^-1 x, then (1 – x²)y ₂ is equal to
(a) xy
(b) xy ₁
(c) xy ₂
(d) x²y
Solution:
(b) We have, y = cos ^-1 x

Question 14.
The degree of the differential equation 1 + (\(\frac{dy}{dx}\))² = x is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) We have, 1 + (\(\frac{dy}{dx}\))² = x
∴ Degree = 2

Question 15.

(a) 1
(b) 2
(c) 3
(d) 4
Solution:

Question 16.
The number of points of discontinuity of f defined by f (x) = |x| – |x +11 is
(a) 1
(b) 2
(c) 0
(d) 5
Solution:
(c) We have, f{x) = |x| – |x + 1|

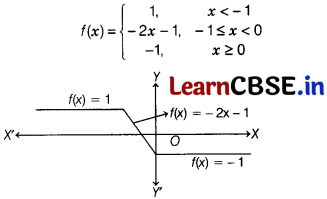
Clearly, f (x) is continuous for all values of x.
Hence, no discontinuous point exist.

Question 17.
\(\int_0^{\pi / 8}\) tan²(2 x) dx is equal to

Solution:

Question 18.
If \(\vec{a}.\vec{b}\) = \(\frac{1}{2}|\vec{a}||\vec{b}|\), then the angle between \(\vec{a}\) and \(\vec{b}\) is
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Solution:
(c) Given, \(\vec{a}.\vec{b}\) = \(\frac{1}{2}|\vec{a}||\vec{b}|\)
⇒ \(\vec{a}.\vec{b}\)cosθ = \(\frac{1}{2}|\vec{a}||\vec{b}|\)
⇒ cos θ = \(\frac{1}{2}\)
⇒ θ = 60°
∴ Angle between \(\vec{a}\) and \(\vec{b}\) is 60°

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.
Assertion (A) A 2 × 2 matrix A = [a _ij ], whose elements are given by a _ij = i × j, is
Reason (R) If A is a 4 × 2 matrix, then the elements in A is 5.
Solution:
(c) Assertion In general, the matrix A of order 2 × 2 is

Now, a _ij = i × j, i = 1, 2 and j = 1,2
∴ a ₁₁ 1 = 1, a ₁₂ = 2, a ₂₁ = 2 and a ₂₂ = 4

Reason If A is a 4 × 2 matrix, then A has 4 × 2 = 8 elements.
Hence, Assertion is true but Reason is false.

Question 20.
Assertion (A) We can write
sin ^-1 x = (sin x) ^-1 .
Reason (R) Any value in the range of principal value branch is called principal value of that inverse trigonometric function.
Solution:
(d) Assertion sin_1x should not be confused with
(sinx) ^-1 . Infact (sinx) ^-1 = \(\frac{1}{\sin x}\) and similarly for other trigonometric functions.

Reason The value of an inverse trigonometric function which lies in the range of principle branch, is called the principal value of that inverse trigonometric function.
Hence, we can say that Assertion is false but Reason is true.

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Find \(\vec{a}\) and \(\vec{b}\), if \(\vec{a}\) = 2\(\vec{b}\) and \((\vec{a}+\vec{b}).(\vec{a}-\vec{b})\) = 12.
Or
Find the unit vector perpendicular to each of the vectors \(\vec{a}\) = 4\(\hat{i}\) + 3\(\hat{j}\) + \(\hat{k}\) and \(\vec{b}\) = 2\(\hat{i}\) – \(\hat{j}\) + 2\(\hat{k}\).
Solution:

Now, perpendicular vector to the given vector is

Question 22.
Check, if the relation R on the set A = {1, 2, 3, 4, 5, 6}, then defined as R = {(x, y): y is divisible by x} is
(i) symmetric
(ii) transitive.
Or
Find the value of tan ^-1 (1) + cos ^-1 (-\(\frac{1}{2}\)) + sin ^-1 (-\(\frac{1}{2}\)).
Solution:
(i) For symmetry We observe that 6 is divisible by 2.
This means that (2, 6) ∈ R but 2 is not divisible by 6
i.e. (6, 2) ∉ R. So, R is not symmetric.

(ii) For transitivity Let (x, y) ∈ R and (y, z) ∈ R, then z is divisible by x. i.e. (x, z) ∈ R
e.g. 2 is divisible by 1, 4 is divisible by 2.
So, 4 is divisible by 1. So, R is transitive.
Or
We know that ranges of principle values of

Question 23.
Show that the function

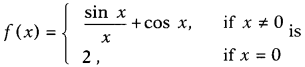
continuous at x = 0.
Solution:

Hence, f(x) is continuous at x = 0. (1)

Question 24.
Show that the function f defined by f(x)-(x- 1)e ^x +1 is an increasing function for all x > 0.
Solution:
We have, f(x) = (x – 1)e ^x + 1
On differentiating w.r.t. x, we get
f'(x) = (x – 1)ex + ex
f’(x) = xe ^x
For all x > 0 ⇒ f'(x) > 0
∴ f(x) is an increasing function for all x > 0.

Question 25.
If a line has direction ratios 2, -1, 2, then determine its direction cosines.
Solution:
Given, direction ratios are (2, -1, 2), i.e. a = 2, b = -1 and c = 2.

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Solve (x + 1)\(\frac{dy}{dx}\) = 2e ^-y + 1; y = 0, when x = 0.
Or
Solve x sin(\(\frac{y}{x}\))\(\frac{dy}{dx}\) + x – ysin(\(\frac{y}{x}\)) = 0; y = \(\frac{\pi}{2}\), when x = 1.
Solution:
Given, differential equation is

⇒ log(e ^y + 2) = log(x + 1) +logC
⇒ log(e ^y + 2) = logC(x + 1)
⇒ e ^y + 2 = C(x + 1)
Also given, y = 0, when x = 0
On putting x – 0 and y = 0 in Eq. (i), we get
e° + 2 = C(0 + 1) ⇒ C = 1 + 2 = 3
On putting value of C in Eq. (i), we get
e ^y + 2 = 3(x + 1)
⇒ e ^y = 3x + 3 – 2 ⇒ e ^y = 3x + 1
⇒ y = log(3x + 1)
Or
Given, differential equation can be written as

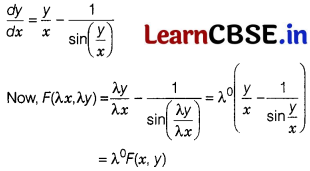
It is a homogeneous differential equation.
Now, on putting y = vx, we get

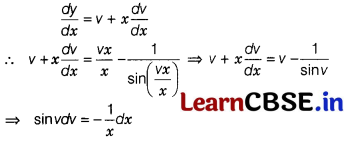
On integrating both sides, we get
– cos v = -log |x| + C
⇒ – cos(\(\frac{y}{x}\)) = -log |x| – C [∵ v = \(\frac{y}{x}\)]
⇒ cos(\(\frac{y}{x}\)) = log |x| – C ………. (i)
Given that x = 1, when y = \(\frac{\pi}{2}\)
∴ cos(\(\frac{\pi}{2}\)) = log|1| + C
⇒ 0 = 0 + C
⇒ C = 0
On putting C = 0 in Eq. (i), we get
cos(\(\frac{y}{x}\)) = log|x| + 0
⇒ cos(\(\frac{y}{x}\)) = log|x|

Question 27.
Find the value of \(\int_0^1 x\) (1 – x) ⁿ dx.

Solution:
Let l = \(\int_0^1 x\) (1 – x) ⁿ dx
⇒ l = \(\int_0^1 x\) (1 – x){1 – (1 – x)} ⁿ dx

On using \(\int_0^2a\)f(x)dx = 2\(\int_0^a\)f(x) dx, if f(2a – x) = f(x),
we get

Question 28.
Find \(\int \frac{x}{x^2+3 x+2} d x\)
Solution:

On substituting the value of l ₁ and l ₂ in Eq. (i), we get

Question 29.
Three rotten apples are mixed with seven fresh apples. Find the probability distribution of the number of rotten apples, if three apples are drawn one by one with replacement, then find the mean of the number of rotten apples.
Or
In a Shop X, 30 tins of ghee of Type A and 40 tins of ghee of Type B which look alike, are kept for sale. While in Shop Y, similar 50 tins of ghee of type A and 60 tins of ghee of Type B are there. One tin of ghee is purchased from one of the randomly selected shop and is found to be of Type B. Find the probability that it is purchased from Shop Y.
Solution:
Given, rotten apples = 3 and fresh apples = 7
Here, total number of apples = 3 + 7 = 10
Let X denotes the number of rotten apples.
Then, X takes the values 0, 1, 2, 3.
Let A be the event getting a rotten apple.
∴ P(A) = \(\frac{3}{10}\) and P(A’) = 1 – P(A) = 1 – \(\frac{3}{10}\) = \(\frac{7}{10}\)
Now, P(X = 0) = P (getting 0 rotten apple)

Now, mean (µ) = ∑X.P(X)

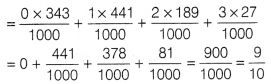
Or
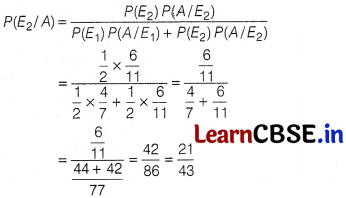
Let E ₁ = Getting ghee from Shop X
E ₂ = Getting ghee from Shop Y
A = Getting Type B ghee
∴ P(E ₁ ) = P(E ₂ ) = \(\frac{1}{2}\) [∵ both shop have equal chances]
P(A/E ₁ ) = Probability that Type B ghee is purchased from Shop X
\(\frac{40}{70}\) = \(\frac{4}{7}\)
P(A/E ₂ ) = Probability that Type B ghee is purchased from Shop Y
\(\frac{60}{110}\) = \(\frac{6}{11}\)
Now, by Baye’s theorem, we get

Question 30.
If Z = 2x + 3y, subject to constraints x + 2y ≤ 10, 2x + y ≤ 14, x, y ≥ 0, then find the corner points of feasible region.
Solution:
Given, Z = 2x + 3y
Subject to constraints
x + 2y ≤ 10 …(i)
2x + y ≤ 14 …(ii)
and x, y ≥ 0 …(iii)
Shade the region to the right of Y-axis to show x ≥ 0 and above X-axis to show y ≥ 0.
Table for line x + 2y = 10 is

So, the line is passing through the points (0, 5), (4, 3) and (10, 0).

On putting (0, 0) in the inequality x + 2y ≤ 10, we get 0 + 0 ≤ 10, which is true.
So, the half plane is towards the origin.
Table for line 2x + y = 14 is

So, the line is passing through the points (4, 6), (6,2) and (7, 0).
On putting (0, 0) in the inequality 2x + y ≤ 14, we get 0 + 0 ≤ 14, which is true.
So, the half plane is towards the origin.
The intersection point of lines corresponding to Eqs. (i) and (ii) is 6(6, 2).
On shading the common region, we get the feasible region OABDO.

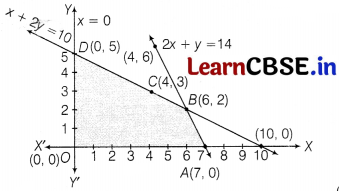
The corner points are 0(0, 0), 4(7, 0), 6(6, 2) and D(0, 5).

Question 31.
Evaluate \(\int_0^1\)x(tan ^-1 x)dx.
Solution:

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.
Find the area of the smaller part of the circle x²+ y² = a² cut-off by the line x = \(\frac{a}{\sqrt{2}}\)
Solution:
Given equations of circle and line are
x²+ y² = a²
and \(\frac{a}{\sqrt{2}}\) ….. (ii)

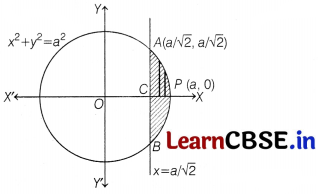
Clearly, required region is APBCA, which is symmetrical about X-axis, and the x-coordinate of
point of intersection curve and line is \(\frac{a}{\sqrt{2}}\).
Now, required area = Area of region APBCA
= 2 (Area of region APCA)

Question 33.
Prove that the relation R on Z, defined by R{(a, b) :(a – b) is divisible by 5} is an equivalence relation.
Or
Show that the relation R in the set A of points in a plane, given by R = {(P, Q): distance of the point P from the origin is same as the distance of the point Q from the origin}, is an equivalence relation. Further, show that the set of all points related to a point P ≠ (0, 0) is the circle passing through P with origin as centre.
Solution:
Given, R = {(a, b): 5divides (a – b)}
and Z = Set of integers
Reflexive Let a e Z be any arbitrary element.
Now, if (a, a) ∈ R, then 5 divides a-a, which is true.
So, R is reflexive.
Symmetric Let a, to ∈ Z, such that
(a, b) ∈ R ⇒ 5 divides (a – to)
⇒ 5 divides [- (a – b)]
⇒ 5 divides (b – a)
⇒ (b, a) e R
So, R is symmetric.

Transitive Let a, b, c ∈ Z, such that (a, b) ∈ R and (b, c) ∈ R
⇒ a-b and to -c both are divisible by 5.
⇒ a – b + b – c is divisible by 5.
⇒ (a – c) is divisible by 5.
⇒ (a, c) ∈ R
So, R is transitive.
Thus, R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation.
Or
Here, R = {(P, G): distance of point P from the origin is same as the distance of point Q from the origin}.
Clearly, (P, P) ∈ R, since the distance of point P from the origin is always the same as the distance of the same point P from the origin.
Therefore, R is reflexive.
Now, let (P, Q) ∈ R.
⇒ The distance of point P from the origin is same as the distance of point Q from the origin.
⇒ The distance of point Q from the origin is same as the distance of point P from the origin.
⇒ (G, P) ∈ R
Therefore, R is symmetric.
Now, let (P, Q),(Q, S) ∈ P
The distance of points P and 0 from the origin is same and also the distance of points Q and S from the origin is same.
⇒ The distance of points P and S from the origin is same.
⇒ (P, S) ∈ P
Therefore, ft is transitive.
Therefore, R is an equivalence relation.
The set of all points related to P ≠ (0, 0) will be those points whose distance from the origin is the same as the distance of point P from the origin.
In other words, if O(0, 0) is the origin and OP = k, then the set of all points related to P is at a distance of k from the origin.
Hence, this set of points forms a circle with the centre £s the origin and this circle passes through point P.

Question 34.
Find the vector and cartesian equations of the line which is perpendicular to the

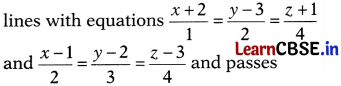
through the point (1, 1, 1). Also, find the angle between the given lines.
Or
Find the shortest distance between the lines given by
\(\vec{r}\) = (2 + λ)\(\hat{i}\) – (3 + λ)\(\hat{j}\) +(5 + λ)\(\hat{k}\)
and \(\vec{r}\) = (2µ – 1)\(\hat{i}\) + (4µ – 1)\(\hat{j}\) + (5 – 3µ)\(\hat{k}\).
Solution:
Any line through the point (1, 1, 1) is given by
\(\frac{x-1}{a}=\frac{y-1}{b}=\frac{z-1}{c}/latex] …(i)
where a, b and c are the direction ratios of line (i).
Now, the line (i) is perpendicular to the lines
lines are (1, 2, 4) and (2, 3, 4), respectively.
∴ a + 2b + 4c = 0 …(ii)
and 2a + 3b + 4c = 0 … (iii)
[∵ if two lines having DR’s (a ₁ , b ₁ , c ₁ )and (a ₂ , b ₂ , c ₂ ) are perpendicular, then a ₁ a ₂ + b ₁ b ₂ + c ₁ c ₂ = 0]
By cross-multiplication method, we get

∴ DR’s of line (i) are – 4, 4, -1.
∴ The required cartesian equation of line (i) is
[latex]\frac{x-1}{-4}=\frac{y-1}{4}=\frac{z-1}{-1}/latex]
and vector equation is
[latex]\vec{r}\) = \(\hat{i}+\hat{j}+\hat{k}\) + λ(\(-4\hat{i}+4\hat{j}-\hat{k}\))
Again, let θ be the angle between the given lines.
Then,

Or
Given, equation of lines can be rewritten as
\(\vec{r}\) = \(2\hat{i}-3\hat{j}+5\hat{k}\) + λ(\(\hat{i}-\hat{j}+\hat{k}\))
and \(\vec{r}\) = \(-\hat{i}-\hat{j}+5\hat{k}\) + µ(\(2\hat{i}+4\hat{j}-3\hat{k}\))
On comparing the above equations with standard
vector form of equation of line, \(\vec{r}\) = \(\vec{a}\) + λ\(\vec{b}\), we get

Question 35.

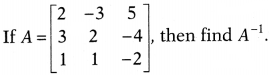
Using A ^-1 solve the following system of equations
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = -3
Solution:


Now, to find the solution of system equations
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = -3
Given, system of equations can be written in matrix form as

On comparing the corresponding elements, we get x = 1, y = 2 and z = 3

Common Mistake Students determine cofactors without taking proper sign. They do not take transpose of a matrix obtained from the cofactors.

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
P(x) = -6x² + 120x + 25000 (in ₹) is the total profit function of a company, where x denotes the production of the company.

Based on the above information, answer the following questions.
(i) Find the profit of the company, when the production is 3 units.
(ii) Find P'(5).
(iii) Find the interval in which the profit is strictly increasing.
Or
Find the production, when the profit is maximum.
Solution:
(i) At x = 3,
P (3) = -6 (3)² f + 120 (3) + 25000
= -54 + 360 + 25000
= ₹ 25306

(ii) P'(x) = -12x + 120
P'(5) = -12 × 5 + 120
= -60 + 120 = 60

(iii) For strictly increasing, we must put P'(x) > 0
⇒ -12x + 120 > 0
⇒ 120 > 12x (1)
⇒ x < 10
∴ x ∈ (0, 10)
Or
P(x) = -6x² + 120x + 25000
⇒ P'(x) = – 12x + 120
For maximum profit, put P'(x) = 0
⇒ x = 10
Now, P”(x) = -12 < 0
∴ At x = 10, profit function is maximum.

Question 37.
In a college, an architecture design a auditorium for its cultural activities purpose. The shape of the floor of the auditorium is rectangular and it has a fixed perimeter, say P.

Based on the above information, answer the following questions.
(i) If l and b represents the length and breadth of the rectangular region, then find the relationship between l, b and P.
(ii) Find the area (A) of the floor, as a function of l.
(iii) College manager is interested in maximising the area of the floor A.
For this purpose, find the value of l.
Or
Find the maximum area of the floor.
Solution:
(i) Perimeter of rectangular floor
= 2 (length + breadth)
⇒ P = 2(1 + b)

(ii) Area, A = length × breadth
A = I × b ,..(i)
∵ P =2(l + b)
⇒ \(\frac{P}{2}\) = l + b
⇒ \(\frac{P}{2}\) – l = b ⇒ \(\frac{P – 2l}{2}\) = b
From Eq. (i),

Question 38.
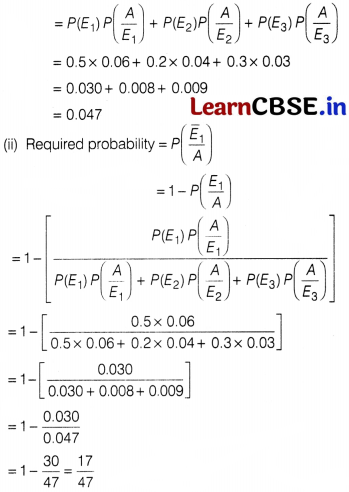
In an office three employees Vinav, Sonia and Iqbal process incoming copies of a certain form. Vinav process 50% of the forms. Sonia processes 20% and Iqbal the remaining 30% of the forms. Vinay has an error rate of 0.06, Sonia has an error rate of 0.04 and Iqbal has an error rate of 0.03.

Based on the above information answer the following questions.
(i) The total probability of committing an error in processing the form.
(ii) The manager of the company wants to do a quality check. During inspection he selects a form at random from the days output of processed forms. If the form selected at random has an error, the probability that the form is not processed by Vinay.
Solution:
Let E ₁ = Event of processing form by vinay.
E ₂ = Event of processing form by Sonia.
E ₃ = Event of processing form by Iqbal.
and A = Event of committing an error.
(i) Required probability = P(A)