CBSE Sample Papers for Class 12 Maths Set 10 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 12 Maths with Solutions Set 10 are designed as per the revised syllabus.

CBSE Sample Papers for Class 12 Maths Set 10 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
Let \(\vec{a}=\hat{i}-2\hat{j}+3\hat{k}\). If \(\vec{b}\) is a vector such that \(\vec{a}.\vec{b}=|\vec{b}|^2\) and|\(\vec{a}-\vec{b}\)| = √7, then|\(\vec{b}\)| is equal to
(a) 7
(b) 14
(c) √7
(d) 21
Solution:

Question 2.

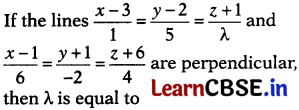
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(a) Given lines are

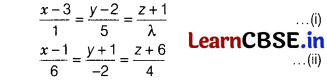
∵ Lines (i) and (ii) are perpendicular.
∴ 1(6) + 5(-2) + λ(4) = 0
⇒ 6 – 10 + 4λ = 0
⇒ 4λ = 4
⇒ λ = 1

Question 3.
If A is a matrix of order 3 such that A(adj.A) = 10I. Then, the value of |adj A| is
(a) 10
(b) 100
(c) 110
(d) 5
Solution:
(b) We have, A . (adj A) = 10 . l
We know that A(adj A) = |A| . l
∴ |A| = 10
Also, we know that |adj A| = |A| ^n-1
∴ |adj A| = (10)² = 100 [∵ n = 3]

Question 4.
If \(\vec{a}\) and \(\vec{b}\) are two unit vectors such that \(\vec{a}+\vec{b}\) is also a unit vector, then the angle between \(\vec{a}\) and \(\vec{b}\) is
(a) π
(b) \(\frac{\pi}{2}\)
(c) \(\frac{\pi}{3}\)
(d) \(\frac{2\pi}{3}\)
Solution:

Hence, the angle between \(\vec{a}\) and \(\vec{b}\) is \(\frac{2\pi}{3}\).

Question 5.
The function defined by

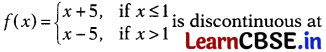
(a) x = 0
(b) x = 1
(c) x = 2
(d) None of these
Solution:

Thus, f(x) is not continuous at x = 1.

Question 6.
The projection of (\(\vec{b}+\vec{c}\)) on \(\vec{a}\),

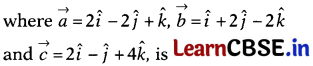
(a) 1
(b) 2
(c) 3
(d) 4
Solution:

Question 7.
Vector equation of the line

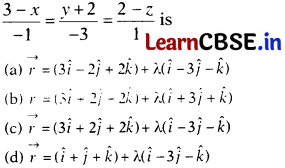
Solution:
(a) Given equation of line can be rewritten as
\(\frac{x-3}{1}=\frac{y-(-2)}{-3}=\frac{z-2}{-1}\)
⇒ (x, y, z) = (3, -2, 2)
and (a, b, c) = (1, -3, -1)
∴ Required vector equation of line is given by
\(\vec{r}=(3\hat{i}-2\hat{j}+2\hat{k})+\lambda(\hat{i}-3\hat{j}-\hat{k})\)

Question 8.
\(\int_1^e\)log x dx is equal to
(a) 1
(b) 2
(c) 3
(d) 4
Solution:

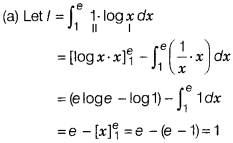
Question 9.
The value of λ, if the vectors \(2\hat{i}+\lambda\hat{j}+3\hat{k}\) and \(3\hat{i}+2\lambda\hat{j}-4\hat{k}\) are perpendicular to each other, is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:

Question 10.
The function f(x) = \(\frac{9-x^2}{9x-x^3}\) is
(a) discontinuous at only one point
(b) discontinuous at exactly two points
(c) discontinuous at exactly three points
(d) None of the above
Solution:

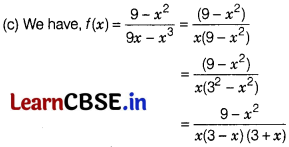
Clearly, f(x) is discontinuous at exactly three points
x = 0, x = -3 and x = 3.

Question 11.
∫ \(\frac{sin^6x}{cos^8x}\)dx is equal to

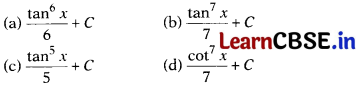
Solution:

Question 12.
If |\(\vec{a}\)| = 2, |\(\vec{b}\)| = 5 and \(\vec{a}.\vec{b}\) = 2, then |\(\vec{a}-\vec{b}\)| is equal to
(a) 1
(b) 5
(c) -1
(d) 4
Solution:
(a) We have,

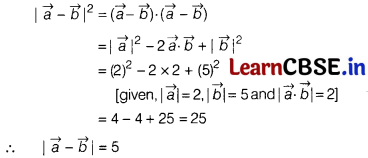
Question 13.
The cartesian equation of the line which passes through the point (-2, 4, -5) and is

Solution:
(a) The required line is parallel to the line

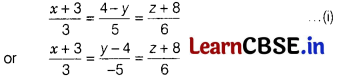
∴ Direction ratios of this line are 3, – 5 and 6 also the required line passes through the point (-2, 4, -5).
∴ The cartesian equation of the required line is given by
\(\frac{x+2}{3}=\frac{y-4)}{-5}=\frac{z+5}{6}\)

Question 14.
The solution of differential equation \(\frac{dy}{dx}+\frac{y}{x}\) = sin x is
(a) x(y + cos x) = sin x + C
(b) x(y – cos x) = sin x + C
(c) xy cos x = sin x + C
(d) x(y + cos x) = cos x + C
Solution:
(a) Given differential equation is
\(\frac{dy}{dx}+y\frac{1}{x}\) = sin x
which is a linear differential equation.
Here, P(x) = \(\frac{1}{x}\) and Q(x) = sin x x
∴ IF = e ^{∫\(\frac{1}{x}\)dx} = e ^{log x} = x
The general solution is
y.x = ∫(x. sin x)dx + C
⇒ xy = -x cos x + sin x + C [using integration by parts]
⇒ x(y + cos x) = sin x + C

Question 15.
If the function f is given by f(x) = x³ – 3x² +4x, x ∈ R, then
(a) f is strictly increasing on R.
(b) f is decreasing on R.
(c) f is neither increasing nor decreasing on R.
(d) f is strictly decreasing on R.
Solution:
(a) We have, f(x) = x³ – 3x² + 4x, where x ∈ R
f'(x) = 3x² – 6x + 4= 3(x² -2x + 1) + 1
= 3(x – 1)² + 1 > 0 ∀ x ∈ R
Therefore, the function f is strictly increasing on R.

Question 16.
If A is skew-symmetric matrix, then A2 is
(a) symmetric matrix
(b) skew-symmetric matrix
(c) null matrix
(d) None of the above
Solution:
(a) (A²) = (A’)² = (-A)² = A²
Hence, A² is symmetric matrix.

Question 17.
Area of the region bounded by y² = 9x, x = 2, x = 4 and the X-axis in the first quadrant, is
(a) 4(4 – √2)sq units
(b) \(\frac{8}{3}\)(4 – √2) sq units
(c) 3(4 – √2) sq units
(d) \(\frac{14}{3}\) sq units
Solution:
(a) Since, the given curve y² = 9x is a parabola which is symmetrical about X-axis (as the power of y is even) and passes through the origin.

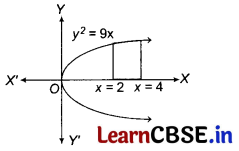
The area of the region bounded by the curve y² = 9x, x = 2 and x = 4 and the X-axis is the area shown in the figure.
Required area (shaded region)

Question 18.
Area of the region bounded by x² = 4y, y = 2, y = 4 and the Y-axis in the first quadrant, is
(a) 4(4 – √2)sq units
(b) \(\frac{8}{3}\)(4 – √2) sq units
(c) 3(4 – √2) sq units
(d) \(\frac{14}{3}\) sq units
Solution:
(b) The given curve x² = 4y is a parabola which is symmetrical about Y-axis (since, it contains even power of x only) and passes through the origin.

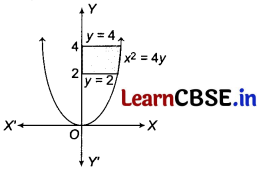
The area of the region bounded by the curve x² = Ay, y = 2 and y = 4 and the Y-axis is shown in the figure.

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.

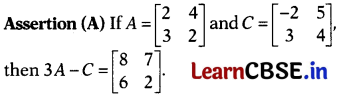
Reason (R) If the matrices A and B are of same order, say mxn, satisfy the commutative law, then A + B = B + A.
Solution:

Hence, both Assertion and Reason are true but Reason is not the correct explanation

Question 20.
Let R be any relation in the set A of human beings in a town at a particular time.
Assertion (A) If R = {(x, y): x is wife of y}, then R is reflexive.
Reason (R) If R = {(x, y): x is father of y}, then R is neither reflexive nor symmetric nor transitive.
Solution:
(d) Assertion Here R is not reflexive, as x cannot be wife of x
Here, Assertion is false.
Reason Here, R is not reflexive, as x cannot be father of x, for any x. R is not symmetric as if x is father of y, then y cannot be father of x. R is not transitive as if x is father of y and y is father of z, then x is grandfather (not father) of z.
Hence, Reason is true.

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Evaluate \(\int_{-\pi}^{\pi}\) (1 -x²)sin x cos² xdx.
Or
Evaluate \(\int_{-1}^2\frac{|x|}{x}\)dx.
Solution:
Let l = \(\int_{-\pi}^{\pi}\)(1 – x²)sin x cos²x dx
Again, let/(x) = (1 – x²)sin x cos²x
∴ f(-x) = [1 – (-x)²]sin (-x)cos²(-x)
= (1 – x²)(-sin x)cos²x
= -(1 – x²) sin x cos² x = -f(x)
∴ f(x) is odd function
∴ l = 0 [∵ \(\int_{-\pi}^{\pi}\)f(x)dx = 0, if /(x)is an odd function]

Question 22.
Solve the differential equation cos(\(\frac{dy}{dx}\)) = a, (a ∈ R).
Solution:
Given equation is cos (\(\frac{dy}{dx}\)) = a
which can be rewritten as \(\frac{dy}{dx}\) = cos ^-1 a
⇒ dy = cos ^-1 a dx
⇒ ∫dy = ∫(cos ^-1 a)dx ⇒ y = x(cos ^-1 a) + C
which is the required solution.

Question 23.
Check the injectivity of the function f : R → R given by f(x) = x³.
Or
Show that the function f : R → R, given by f(x) = cos x, ∀ x ∈ R is neither one-one nor onto.
Solution:
Let x ₁ , x ₂ ∈ R, such that f(x ₁ ) = f(x ₂ )

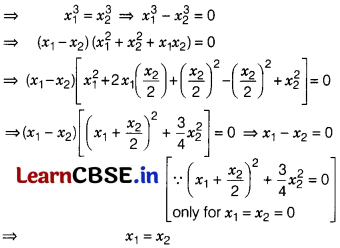
Hence, f is one-one i.e. f is injective.
Or
We have a function f : R → R, defined by
f(x) = cos x
∴ f(0) = cos 0 = 1 and f(2π) = cos 2π = 1
So, f is not one-one.
Also, range of f = [-1, 1] ≠ R
Hence, f is not onto.

Question 24.
Find the value of cos ^-1 (\(\frac{1}{2}\)) + 2 sin ^-1 (\(\frac{1}{2}\)).
Solution:

Question 25.
Find the area of the triangle whose vertices are (-2, -3), (3, 2) and (-1, -8).
Solution:
The area of triangle with vertices (x ₁ , y ₁ ), (x ₂ , y ₂ ) and (x ₃ , y ₃ ) is given by

Since, area is always positive, so we neglect the negative sign.
Hence, the area of triangle is 15 sq units.

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Sketch the graph of y = |x + 3| and evaluate the area under the curve y = |x + 3| above X-axis and between x = -6 to x = 0.
Solution:
First, we sketch the graph of y = |x + 3|

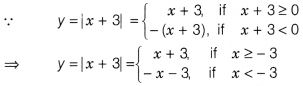
So, we have y = x + 3 for x ≥ -3 and y = -x – 3 for x < -3.
The sketch of y = | x + 3| is shown below

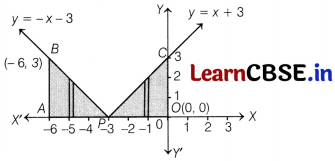
Here, y = x + 3 is the straight line which cuts X and Y-axes at (- 3, 0) and (0, 3), respectively.
Thus, y = x + 3 for x ≥ -3 represents the part of line which lies on the right side of x = – 3.
Similarly, y = -x – 3, x < -3 represents the part of line y = -x – 3, which lies on left side of x = – 3.
Clearly, required area
= Area of region ABPA + Area of region PCOP

Question 27.
Examine the continuity of

If x ^y = e ^x-y , then prove that \(\frac{dy}{dx}=\frac{logx}{(1+log x)^2}\)
Solution:

Thus, LHL = RHL = f(2)
∴ f(x) is continuous at x = 2.

Question 28.
If cos ^-1 x + cos ^-1 y + cos ^-1 z = π, then peove that x² + y² + z² + 2xyz = 1
Or
Find the value of x² + y² + z² + 2xyz, if sin ^-1 x + sin ^-1 y + sin ^-1 z = \(\frac{\pi}{2}\)
Solution:
Let cos ^-1 x = α, cos ^-1 y = β and cos ^-1 z = γ
⇒ cos α = x, cos β = y and cos γ = z
Since, α + β + γ = π
α + β = π – γ
Now, cos (α + β) = cos (π – γ)
⇒ cosα cosβ – sinα sinβ = -cos γ

On squaring on both sides, we get
⇒ (1 – x²)(1 – y²) = (xy+z)²
⇒ 1 – x² – y² + x²y² = x²y² + z² + 2 xyz
⇒ x² + y² + z² + 2xyz = 1

Question 29.
If A (3, 5, -4), 5 (-1, 1, 2)andC(-5, -5, -2) are the vertices of a ∆ABC, then find the direction cosines of AB, AC and BC.
Or
Find the equation of the line passing through the point (1, 2, -4) and perpendicular to the two lines

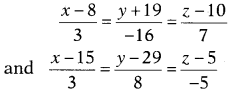
Solution:
Let the vertices of the triangle be A(3, 5, -4), S(-1, 1, 2) and C(-5, -5, -2), respectively

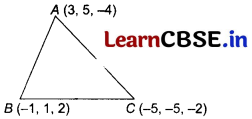
The direction ratios of side 46 are (-1 -3, 1 – 5, 2-(-4))

Therefore, the direction cosines of AC are

Hence, the required equation of line is

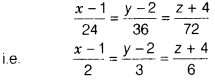
Question 30.
Find the value of a, if the function f(x)

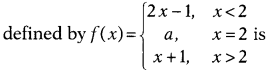
continuous at x = 2.
Solution:

and f(2) = a
From Eq. (i), we have
3 = 3 = a ⇒ a = 3

Question 31.
Prove that the three vectors given below are mutually perpendicular to each other.

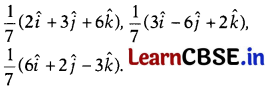
Solution:


Hence, the given three vectors are mutually perpendicular to each other.

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.
Solve the following differential equation.

Solution:
Given differential equation is

which is the required solution.

Question 33.
Solve the LPP
Objective function Z = 3x + 3.5y (maximise), subject to constraints are
x + 2y ≥ 240
3x + 1.5y ≥ 270
1.5x + 2y ≤ 310
x ≥ 0, y ≥ 0
Or
Solve the following LPP by graphical method minimise Z = 20x + 10y Subject to constraints are
x + 2 y ≤ 40,
3x + y ≥ 30
4x + 3y ≥ 60
and x, y ≥ 0
Solution:
Our problem is to maximise Z = 3x + 3.5 y
Subject to the constraints x + 2y ≥ 240
3x + 1.5y ≥ 270
1.5x + 2y ≤ 310 and x ≥ 0, y ≥ 0

Consider the above inequality as equation, we get
x + 2y =240 ….(i)
3x + 1.5y =270 …(ii)
1.5x + 2y = 310 …(iii)
and x = 0, y = 0 ….(iv)
Table for the line x + 2y = 240 is

x	0	240
y	120	0

So, line x + 2y = 240 passes through the points (0, 120) and (240, 0).
On putting (0, 0) in the inequality x + 2y ≥ 240, we get
0 + 2 x 0 ≥ 240
⇒ 0 ≥ 240 (false)
So, the half plane is away from the origin. Table for the line 3x + 1.5y = 270

x	0	90
y	180	0

So, line 3x + 1.5y = 270 passes through the points (0, 180) and (90, 0).
On putting (0, 0) in the inequality 3x + 1,5y ≥ 270, we get
3 × 0 + 1.5 × 0 ≥ 270
⇒ 0 ≥ 270 (false)
So, the half plane is away from the origin.
Table for the line 1.5x + 2y = 310 is

x	0	620/3
y	155	0

So, line 1.5x + 2y = 310 passes through the points (0, 155) and (\(\frac{620}{3}\), 0).

On putting (0, 0) in the inequality 1.5x + 2y ≤ 310, we get
1.5 × 0 + 2 × 0 ≤ 310 ⇒ 0 ≤ 310 (true)
So, the half plane is towards the origin.
The intersection point of lines (ii) and (iii) is B(20, 140), of lines (iii) and (i) is A(140, 50), of lines (i) and (ii) is C(40, 100). Since, x, y ≥ 0,
So, the feasible region lies in the first quadrant.
On plotting the graph, we get the feasible region CABC, whose corner points are C(40,100),
A (140, 50) and 6(20, 140).

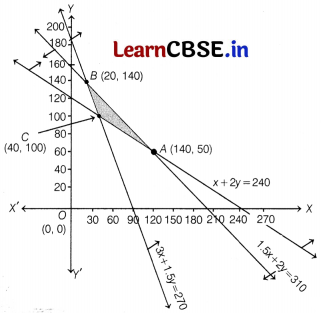
Now, the values of Z at these points are as follows

Corner points	Z = 3x + 3.5y
4(140, 50)	Z = 3 × 140 + 3.5 × 50 = 595 (Maximum)
B(20, 140)	Z = 3 × 20 + 3.5 × 140= 550
C(40, 100)	Z = 3 × 40 + 3.5 × 100 = 470

The maximum value of Z is 595 and it is occur at A(140, 50).

Or

Converting the given inequations into equations, we obtain the following equations
x + 2y = 40, 3x + y = 30, 4x + 3y = 60, x = 0 and y = 0

Region represented by x + 2y ≤ 40 The line x + 2y = 40 meets the coordinate axes at A ₁ (40, 0) and B ₁ (0, 20) respectively. Join these points to obtain the line x + 2y = 40.
Clearly, (0, 0) satisfies the inequation x + 2y ≤ 40.
So, the region in XY-plane that contains the origin represents the solution set of this inequation.

Region represented by 3x + y ≥ 30: The line 3x + y = 30 meets X and Y-axes at A ₂ (10, 0) and B ₂ (0, 30) respectively. Join these points to obtain this line. We find that the point O(0, 0) does not satisfy the inequation 3x + y > 30. So, that region in xy-plane which does not contain the origin is the solution set of this inequation.

Region represented by 4x + 3y ≥ 60 The line 4x + 3y = 60 meets X and Y-axes at A ₃ (15, 0) and B ₁ (0, 20) respectively. Join these points to obtain the line 4x + 3y = 60.

We observe that the point 0 (0, 0) does not satisfy the inequation 4x+ 3y ≥ 60. So, the region not containing the origin in XY-plane represents the solution set of this inequation.

Region represented by x ≥ 0, y ≥ 0 Clearly, the region represented by the non-negativity restrictions x ≥ 0 and y ≥ 0 is the first quadrant in XY-plane.

The shaded region A ₃ A ₁ QP in figure represents the common region of the regions represented by the above inequations. This region expresents the feasible region of the given LPP.

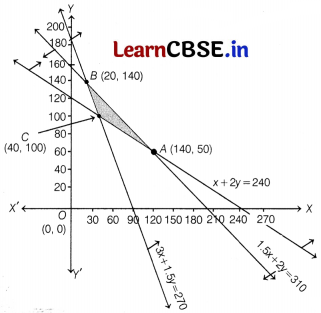
The coordinates of the corner points of the shaded feasible region are A ₃ (15, 0), A ₁ (40, 0), Q(4, 18) and P(6, 12). These points have been obtained by solving the equations of the corresponding intersecting lines, simultaneously.

The values of the objective function at these points are given in the following table

Corner points	Value of the objective function Z =20x + 10y
A 3 (15, 0)	Z = 20 × 15 + 10 × 0 = 300
A 1 (40, 0)	Z = 20 × 40 + 10 × 0 = 800
Q(4, 18)	Z = 20 × 4 + 10 × 18 = 260
P(6, 12)	Z = 20 × 6 + 10 × 12 = 240

Out of these values of Z, the minimum value is 240 which is attained at point P (6,12). Hence, x = 6, y = 12 is the optimal solution of the given LPP and the optimal value of Z is 240.

Question 34.

solve the system of linear equation
x + 2y + z = 4,
-x + y + z = 0,
x – 3 y + z = 2.
Solution:

Now, let us find the cofactors C _ij of elements a _ij in A.

which is the required solution.

Question 35.

Solution:

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
For a function f(x), if f(-x) – f(x), then f(x) is an even function and f(-x) = f(x), then f(x) is a odd function. Again, we have

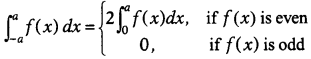
On the basis of above information, answer the following questions
(i) Show that f(x) = x² sin x is an odd function.

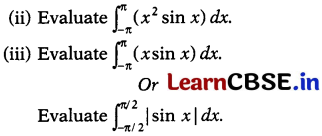
Solution:
(i) We have, f(x) = x² sin x
⇒ f(-x) = (-x)² sin (-x) = -x² sin x = -f(x)
∴ f(x) is odd function.

Question 37.
In a bolt factory, machines A, B and C manufacture respectively 25%, 35% and 40% of the total bolts. Of their output 5%, 4% and 2% are respectively defective bolts.
On the basis of above information, answer the following questions
(i) Find the probability that bolt drawn is defective given that bolt is manufactured by B.
(ii) Find the probability that bolt drawn is defective given that bolt is manufactured by C.
(iii) Find the probability that, if drawn bolt is defective, then it is manufactured by B.
Or
If drawn bolt is defective, then find the probability that it is not manufactured by C.
Solution:
Consider the following events
E ₁ = Bolt is manufactured by machine A
E ₂ = Bolt is manufactured by machine B
E ₃ = Bolt is manufactured by machine C
F = Drawn bolt is defective
We have,

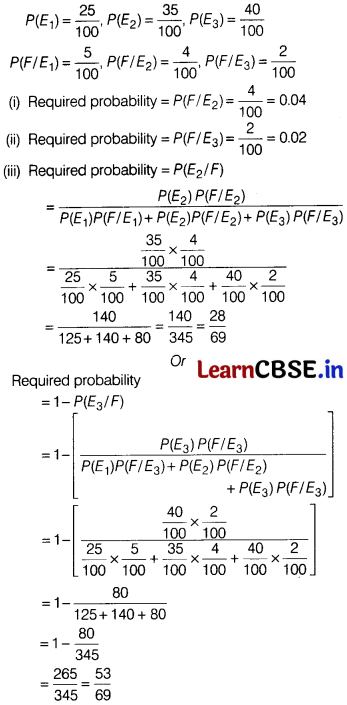
Question 38.
In a test, you either guesses or copies or knows the answer to a multiple choice question with four choice. The probability that you make a guess is \(\frac{1}{3}\), you copies the answer is \(\frac{1}{6}\). The probability that your answer is correct, given that you guess it, is \(\frac{1}{8}\) and also the probability that your answer is correct, given that you copied it is \(\frac{1}{4}\).
On the basis of above information, answer the following questions
(i) Find the probability that you knows the answer, given that you correctly answered it.
(ii) Find the total probability of correctly answered the question.
Solution:
Let E ₁ E ₂ , E ₃ and A be the events defined as follows
E ₁ = You guess the answer
E ₂ = You copies the answer
E ₃ = You knows the answer
A = You answers correctly
Clearly, P(E ₁ ) = \(\frac{1}{3}\) and P(E ₂ ) = \(\frac{1}{6}\)

(i) Since, E ₁ E ₂ and E ₃ are mutually exclusive and exhaustive events.