CBSE Sample Papers for Class 12 Maths Set 1 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 12 Maths with Solutions Set 1 are designed as per the revised syllabus.

CBSE Sample Papers for Class 12 Maths Set 1 with Solutions

Time Allowed: 3 Hours
Maximum Marks: 80

General Instructions:

1. This question paper contains – five sections A, B, C, D and E. Each section is compulsory. However, there are internal choices in some questions.
2. Section A has 18 MCQ’s and 02 Assertion-Reason based questions of 1 mark each.
3. Section B has 5 Very Short Answer (VSA) type questions of 2 marks each.
4. Section C has 6 Short Answer (SA) type questions of 3 marks each.
5. Section D has 4 Long Answer (LA) type questions of 5 marks each.
6. Section E has 3 source based/case/passage based/intergrated units of assessment (4 marks each) with sub-parts.

Section A
(Multiple Choice Questions) Each question carries 1 mark

Question 1.
If A = [ciij] is a square matrix of order 2

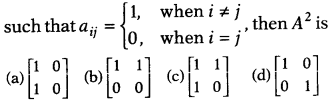
Solution:

Question 2.
If A and B are invertible square matrices of the same order, then which of the following is not correct?
(a) adj A = |A|.A ^-1
(b) det(A) ^-1 = [det(A)] ^-1
(c) (AB) ^-1 = B ^-1 A ^-1
(d) (A + B) ^-1 = B ^-1 + A ^-1
Solution:
(d) (A + B) ^-1 = B ^-1 + A ^-1 is not true.

Question 3.
If the area of the triangle with vertices (-3, 0), (3, 0) and (0, k) is 9 sq units, then the value(s) of k will be
(a) 9
(b) ± 3
(c) -9
(d) 6
Solution:
(b) Area of triangle with vertices
(x ₁ , y ₁ ), (x ₂ , y ₂ ), (x ₃ , y ₃ )

⇒ ±9=3k [given, area = 9sq, units]
⇒ k = ±3units

Question 4.

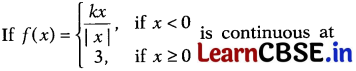
x = 0, then the value of k is
(a) -3
(b) 0
(c) 3
(d) any real number
Solution:
(a) Since, f(x) is continuous at x = 0
∴ LHL = RHL = f{0) = 3

⇒ k = -3

Question 5.
The lines \(\vec{r}\) = \(\hat{i}+\hat{j}-\hat{k}\) + λ(\(2\hat{i} + 3\hat{j} – 6\hat{k}\)) and \(\vec{r}\) = \(2\hat{i} – \hat{j}-\hat{k}\) + µ(\(6\hat{i} + 9\hat{j} – 18\hat{k}\)), (where λ and µ are scalars) are
(a) coincident
(b) skew
(c) intersecting
(d) parallel
Solution:
(d) Given lines are

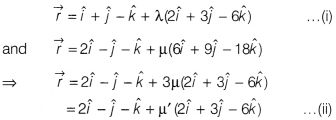
where µ’ = 3µ
Here, the fixed points on the lines are different and the lines l ₁ and l ₂ are parallel to the vector \(2\hat{i}+3\hat{j}-6\hat{k}\).
∴ The lines are parallel to each other.

Question 6.
The degree of the differential equation

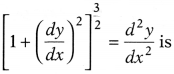
(a) 4
(b) \(\frac{3}{2}\)
(c) 2
(d) Not defined
Solution:

Question 7.
The corner points of the bounded feasible region determined by a system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p, q >0. The condition on p and q, so that the minimum of Z occurs at (3, 0) and (1, 1), is
(a) p = 2q
(b) p = \(\frac{q}{2}\)
(c) p = 3q
(d) p = q
Solution:
(b) Given, objective function Z = px + qy
∵ The minimum occurs at two different point (3, 0) and (1, 1).
∴ p(3) + q(0) = p(1) + q(1)
⇒ 3p = p + q ⇒ p = \(\frac{q}{2}\)

Question 8.
ABCD is a rhombus whose diagonals intersect at E. Then, \(\vec{EA}+\vec{EB}+\vec{EC}+\vec{ED}\) equals to
(a) \(\vec{0}\)
(b) \(\vec{AD}\)
(c) \(2\vec{BD}\)
(d) 2\(\vec{AD}\)
Solution:
(a) We know that diagonals of a rhombus bisect each other.

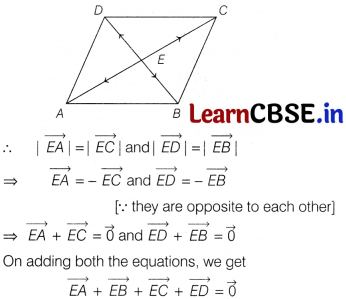
Question 9.
For any integer n, the value of \(\int_0^\pi\)e ^sin²x cos³(2n + 1)x dx is
(a) -1
(b) 0
(c) 1
(d) 2
Solution:

Question 10.
The value of |A|, if

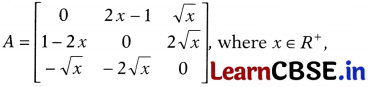
is
(a) (2x + 1)²
(b) 0
(c) (2x +1)³
(d) None of these
Solution:

Question 11.
The feasible region corresponding to the linear constraints of a Linear Programming Problem is given below.

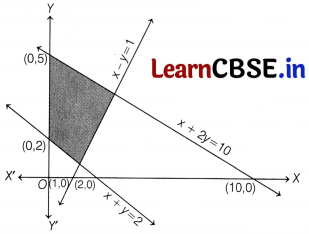
Which of the following is not a constraint to the given Linear Programming Problem?
(a) x + y ≥ 2
(b) x + 2y ≤ 10
(c) x – y ≥ 1
(d) x – y ≤ 1
Solution:
(c) Since, (0, 2) does not satisfy the inequality x – y ≥ 1.
So, the half-plane represented by the above inequality will not contain (0, 2), Therefore, it will not contain the shaded feasible region.

Question 12.
If \(\vec{a}\) = \(4\hat{i}+6\hat{j}\) and \(\vec{b}\) = \(3\hat{j}+4\hat{k}\), then the vector form of the component of \(\vec{a}\) along \(\vec{b}\) is

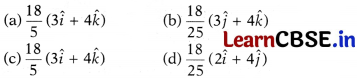
Solution:

Question 13.
Given that A is a square matrix of order 3 and |A| = -2, then |adj (2A)| is equal to
(a) -2 ⁶
(b) 4
(c) -2 ⁸
(d) 2 ⁸
Solution:
(d) Given, |A| = -2
|adj (2A)| = |(2A)| ^3-1 = |2A|² = (2³|A|)² [∵ |adj A| = |A| ^m-1 ]
= 2 ⁶ |A|² = 2 ⁶ × (-2)² = 2 ⁸

Question 14.
A problem in Mathematics is given to three students whose chances of solving it are \(\frac{1}{2},\frac{1}{3},\frac{1}{4}\) respectively. If the events of their solving the problem are independent, then the probability that the problem will be solved, is
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{4}\)
Solution:
(d) Let A, B and C be the respective events of solving the problem.
Then, P(A) = \(\frac{1}{2}\), P{B) = \(\frac{1}{3}\) and P(C) = \(\frac{1}{4}\)
The problem will be solved if one or more of them can solve the problem.
The probability is

Question 15.
The general solution of the differential equation ydx – xdy = 0; (given x, y > 0), is of the form
(a) xy = c
(b) x = cy2²
(c) y =cx
(d) y = cx²
(where c is an arbitrary positive constant of integration)
Solution:
(c) ydx – xdy = 0 ⇒ ydx = xdy
⇒ ∫\(\frac{dx}{x}\) = ∫\(\frac{dy}{y}\)
In x + In C = ln y
Cx = y

Question 16.
The value of λ for which two vectors \(2\hat{i}-\hat{j}+2\hat{k}\) and 3\(\hat{i}\) + λ\(\hat{j}\) + \(\hat{k}\) are perpendicular, is
(a) 2
(b) 4
(c) 6
(d) 8
Solution:

Question 17.
The set of all points, where the function f(x) = x + |x| is differentiable, is
(a) (0, ∞)
(b)(-∞, o)
(c) (-∞, 0) ∪ (0, ∞)
(d) (-∞, ∞)
Solution:

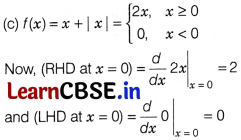
LHD at x = 0 ≠ RHD at x = 0
∴ The function is not differentiable at x = 0.
For x ≥ 0, f(x) = 2x, which is a linear function, and when x < 0, f(x) = 0 which is a constant function.
∴ f(x) is differentiable when x ∈ (- ∞, 0) ∪ (0, ∞).

Question 18.
If the direction cosines of a line are <\(\frac{1}{c},\frac{1}{c},\frac{1}{c}\)>
(a) 0 < c < 1 (b) c > 2
(c) c ± √2
(d) c = ± √3
Solution:

Assertion-Reason Based Questions
In the following questions, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct answer out of the following choices.
(a) Both A and R are true and R is the correct explanation of A
(b) Both A and R are true but R is not the correct explanation of A
(c) A is true but R is false
(d) A is false but R is true

Question 19.
Let f(x) be a polynomial function of degree 6 such that
\(\frac{d}{dx}\)[f(x)] = (x- 1)³ (x – 3)², then
Assertion (A) fix) has a minimum at x = 1.
Reason (R) When \(\frac{d}{dx}\) [f(x)] < 0,
∀ x ∈ (a – h, a) and \(\frac{d}{dx}\)[f(x)] > 0,
∀ x ∈ (a, a + h)’, where h is an infinitesimally small positive quantity, then f(x) has a minimum at x = a, provided fix) is continuous at x- a.
Solution:
(a) Given, \(\frac{d}{dx}\) [f(x)] = (x – 1)³(x – 3)²
On putting \(\frac{d}{dx}\) f(x) = 0 ⇒ (x – 1)³ (x – 3)² = 0
∴ x = 1 and x = 3
∵ \(\frac{d}{dx}\) [f(x)] < 0, ∀ x ∈ (1 – h, 1) and \(\frac{d}{dx}\) [/(x)] > 0, ∀ x ∈ (1, 1 + h)
∴ f(x) has a minimum at x = 1
∴ Both Assertion and Reason are true and Reason is the correct explanation of Assertion.

Question 20.
Assertion (A) The relation
f : (1, 2, 3, 4} → {x, y, z, p} defined by f = {(1, x), (2, y), (3, z)} is a bijective function.
Reason (R) The function
f : (1, 2, 3} → {x, y, z, p} such that
f = {(1, x), (2, y), (3, z)} is one-one.
Solution:
(d) Given relation, f:{1,2, 3, 4} → {x, y, z, p}
and f = {(1, x), (2, y), (3, z)}
Since, 4 has no image under f, so relation f is not a function.
∴ Assertion is false.
Now, f: {1,2, 3} → {x, y, z, p}
and f = {(1, x), (2, y),(3,z)}
Since, every element {1,2, 3} has different image in {x, y, z, p} underf, so the given relation f is one-one.
∴ Reason is true.

Section B
(This section comprises of very short answer type questions (VSA) of 2 marks each)

Question 21.
Find the value of sin ^-1 [cos(\(\frac{33 \pi}{5}\))]
Or
Find the domain of sin ^-1 (x² – 4).
Solution:

Or
Let y = sin ^-1 (x² – 4) ⇒ sin y = x² – 4
i.e. -1 ≤ x² – 4 ≤ 1 [∵ -1 ≤ sin y ≤ 1]
⇒ 3 ≤ x² ≤ 5
⇒ x ∈ [-√5, – √3] u [√3, √5]

Question 22.
Find the interval/s in which the function
f : R → R defined by f(x) = xe ^x , is increasing.
Solution:
Given, f(x) = xe ^x
On differentiating w.r.t, x, we get
f'(x) = xe ^x + e ^x = e ^x (x + 1)
For f(x) to be increasing, we have
f'(x) = e ^x (x + 1) ≥ 0
⇒ x ≥ -1 as e ^x > 0, ∀ x ∈ R
Hence, the required interval, where f(x) increases is [-1, ∞)

Question 23.
If f(x) = \(\frac{1}{4 x^2+2 x+1}\), x ∈ R, then find the maximum value of f(x).
Or
Find the maximum profit that a company can make, if the profit function is given by P(x) = 72 +42x – x², where x is the number of units and P is the profit in rupees.
Solution:

Or
Given, P(x) = 72 + 42x + x²
On differentiating w.r.t. x, we get
P'(x) = 42 – 2x
For maximum profit, we put P’ (x) = 0
⇒ 42 – 2x = 0
⇒ x = 21
∴ The maximum value of P(x) is at x = 21
⇒ P(21) = 72+ 42(21) – 21²
= 72 + 882 – 441
= 513
Thus, the maximum profit is ₹ 513.

Question 24.
Evaluate \(\int_{-1}^1\)log _e (\(\frac{2-x}{2+x}\))
Solution:

Question 25.
Check whether the function f: R → R defined by f(x) = x³ + x, has any critical point/s or not? If yes, then find the point/s.
Solution:
Given, f(x) = x³ +x, ∀ x ∈ R
On differentiating w.r.t. x, we get
f'(x)= 3x² + 1
∵ x² > 0, ∀ x ∈ R
∴ f'(x) can never be zero or undefined, ∀ x ∈ R
⇒ f'(x) = 0
Hence, no critical point exists.

Section C
This section comprises of short answer type questions (SA) of 3 marks each

Question 26.
Evaluate \(\frac{2x^2+3}{x^2(x^2+9)}\) dx, x ≠ 0.
Solution:

Question 27.
The random variable X has a probability distribution P(X) of the following form, where ‘k ‘is some real number.

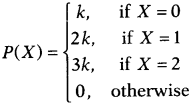
(i) Determine the value of k.
(ii) Find P(X < 2).
(iii) Find P(X > 2).
Solution:
(i) ∑ P(X _i ) = P(X = 0) + P(X = 1) + P(X = 2) + P(otherwise) = 1
⇒ k + 2k + 3k + 0 =
⇒ 6k = 1 ⇒ k = \(\frac{1}{6}\)

(ii) P(X < 2) = P(X = 0) + P(X = 1) ⇒ k + 2k = 3k = 3(\(\frac{1}{6}\)) = \(\frac{1}{2}\)

(iii) P(X > 2) = 0

Question 28.
Evaluate ∫\(\frac{x}{1-x^3}\) dx , x ∈ (0, 1).
Or
Evaluate \(\int_0^\frac{\pi}{4}\)log_e (1 + tan x)dx
Solution:

Or

Question 29.
Solve the differential equation

Or
Solve the differential equation
(cos² x)\(\frac{dy}{dx}\) + y = tan x; (0 ≤ x < \(\frac{33 \pi}{5}\))
Solution:
Given, differential equation is

On comparing with \(\frac{dy}{dx}\) + Py = Q, we get
P = sec² x, Q = (sec² x) tan x
Integrating Factor, IF = e ^∫Pdx
= e ^{∫sec² x dx}
= e ^{tan x}
∴ Solution of the differential equation is
y × IF = ∫ (0 × IF)dx + C
y × e ^{tan x} = ∫ (sec² x) tan x e ^{tan x} dx + C
Let l ₁ = ∫ sec² x tan x e ^{tan x} dx
Let tan x = t
On differentiating w.r.t. x,
sec² x = \(\frac{dt}{dx}\)
⇒ sec² x dx = dt

Using integration by parts, we get
l ₁ = te ^t – e ^t
= tan xe ^{tan x} – e ^{tan x} + C ₁
= e ^{tan x} (tan x – 1) + C ₁
From Eq. (i),
y × e ^{tan x} = e ^{tan x} (tan x – 1) + C ₁
⇒ y = tan x – 1 + (C ₁ + C)e ^{-tan x}

Question 30.
Solve the following Linear Programming Problem graphically
Minimize Z = x + 2 y
subject to the constraints, x + 2 y ≥ 100
2x – y ≤ 0, 2x + y ≤ 200, x, y ≥ 0.
Or
Solve the following Linear Programming
Problem graphically
Maximize Z = – x + 2 y,
subject to the constraints, x ≥ 3, x + y ≥ 5, x + 2y ≥ 6, y ≥ 0.
Solution:
We have, minimize Z = x + 2y ……(i)
and constraints are x + 2y > 100 ……(ii)
2x – y ≤ 0 ……(iii)
2x + y ≤ 200 ……(iv)
x, y ≥ 0 ……(v)
The shaded region is the feasible region ABCD determined by the system of constraints (ii) to (v), which is bounded.

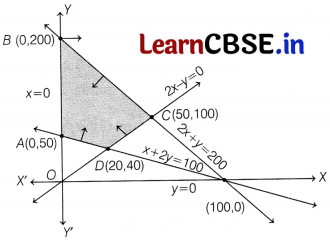
The coordinates of comer points A, B, C and D are (0, 50), (0, 200), (50, 100) and (20, 40), respectively.

Corner Point	Corresponding value of Z = x + 2y
A(0, 50)	Z = 0 + 2(50) = 100 (Minimum)
B(0, 200)	Z = 0 + 2(200) = 400
C(50, 100)	Z = 50+ 2(100) = 250
D(20, 40)	Z = 20 + 2(40) = 100 (Minimum)

The minimum value of Z is 100 at all the points on the line segment joining the points (0, 50) and (20, 40).
Or
We have, maximize Z = – x + 2y ….(i)
and the constraints x ≥ 3 ….(ii)
x + y ≥ 5 ….(iii)
x + 2y ≥ 6 ….(iv)
y ≥ 0 ….(v)
The shaded region is the feasible region determined by the system of constraints (ii) to (v) which is unbounded.

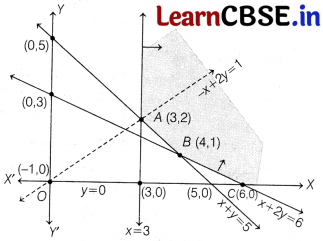
The coordinates of corner points A, B and C are (3, 2) (4, 1) and (6, 0), respectively.

Corner Point	Corresponding value of Z = -x + 2y
A( 3, 2)	Z = -3 + 2(2) = 1
B(4, 1)	Z = -4 + 2(1) = -2
C(6, 0)	Z = -6 + 2(0) = -6

Here, Z = 1 may or may not be the maximum value.

Now, we draw the graph of the inequality – x + 2y > 1 and we check whether the resulting open half-plane has any point in common with the feasible region or not.
Here, the resulting open half plane has points in common with the feasible region.
Hence, Z = 1 is not the maximum value.
∴ Z has no maximum value.

Question 31.
If (a + bx) e ^y/x = x, then prove that
\(x\frac{d^{2}y}{dx^{2}}\) = (\(x\frac{a}{a+bx}\))²
Solution:
Given, (a + bx) e ^y/x = x
⇒ e ^y/x = \(\frac{x}{a+bx}\)
Taking log _e both sides, we get

Section D
This section comprises of long answer type questions (LA) of 5 marks each

Question 32.
Make a rough sketch of the region
{(x, y):0 < y ≤ x² +1,
0 ≤ y ≤ x + 1, 0 ≤ x ≤ 2} and find the area of the region, using the method of integration.
Solution:

Question 33.
Let N be the set of all natural numbers and R be a relation on N × N defined by (a, b)R(c, d) ⇔ ad = be for all.
(a, b), (c, d) ∈ N × N. Show that R is an equivalence relation on N × N. Also, find the equivalence class of (2, 6) i.e. [(2, 6)].
Or
Show that the function f : R-+ {x ∈ R: -1 < x < 1} defined by
f(x) = \(\frac{x}{1+|x|}\), x ∈ R is one-one and onto function.
Solution:
We know that a relation R is an equivalence relation if it is reflexive, symmetric and transitive.
For reflexive
For any (a,b) ∈ N × N
ab = ba [∵ multiplication is commutative on N]
⇒ (a, b) R(a, b) [from definition of relation R on N × N]
Thus, R is reflexive.

For symmetric
Let (a, b), (c, d) be arbitrary elements of N × N
(a,b) R(c,d)
⇒ ad = be
⇒ bc = ad
⇒ cb = da [as a,b,c,d ∈ N and multiplication is commutative on N]
⇒ (c, d) R(a, b)
∴ R is symmetric.

For transitive
Let (a, b), (c, d), (e, f) be arbitrary elements of N × N such that (a, b) R(c, d) and (c, d) R(e, f).
Then, ad = bc and cf = de
⇒ (ad)(cf) = (bc)(de)
⇒ af = be
⇒ (a, b) R(e, f)
∴ R is transitive.
Hence, R is an equivalence relation.

Now, [(2, 6)] = {(x, y) ∈ N × N: (x, y) R(2, 6)}
⇒ 6x = 2y ⇒ 3x = y
∴ [(2, 6)] = {(x, y) ∈ N × N 3x = y}
= {(x, 3x): x ∈ N}
= {(1, 3), (2, 6), (3, 9)…}
Or

⇒ x ₁ + x ₁ x ₂ = x ₂ + x ₁ x ₂ ⇒ x ₁ = x ₂
∴ f(x) is one-one.

Checking onto:
Let f(x) = y, such that y ∈ (-1, 1)
∴ y = \(\frac{x}{1+x}\)
⇒ y + xy = x ⇒ x – xy = y
⇒ x(1 – y) = y ⇒ x = \(\frac{x}{1-y}\)
∵ x is defined at ∀ y ∈ (-1, 1)
∴ f(x) is onto.

Case II When x < 0, we have
f(x) = \(\frac{x}{1-x}\)

Checking one-one :
Let x ₁ , x ₂ ∈ R
f(x ₁ ) = f(x ₂ )
⇒ \(\frac{x_1}{1-x_1}=\frac{x_2}{1-x_2}\)
⇒ x ₁ – x ₂ x ₁ = x ₂ – x ₂ x ₁ ⇒ x ₁ = x ₂
∴ f(x) is one-one.
Checking onto
Let y = f(x) such that y ∈ (-1, 1)
⇒ y = \(\frac{x}{1-x}\) ⇒ y – yx = x ⇒ x = \(\frac{x}{1+y}\)
∴ ∀ y ∈ (-1, 1), x is defined.
∴ f(x) is onto.
Hence, f(x) is one-one and onto function.

Question 34.
Using the matrix method, solve the following system of linear equations.

Solution:
The given system of equations can be written in the form AX = B.

Question 35.
Find the coordinates of the image of the point (1, 6, 3) with respect to the line \(\vec{r}=(\hat{j}+2\hat{k})+\lambda(\hat{i}+2\hat{j}+3\hat{k})\), where λ. is a scalar. Also, find the distance of the image from the F-axis.
Or
An aeroplane is flying along the line
\(\vec{r}=\lambda(\hat{i}-\hat{j}+\hat{k})\), where λ is a scalar and another aeroplane is flying along the line
\(\vec{r}=\hat{i}-\hat{j}+\mu(-2\hat{j}+\hat{k})\), where µ is a scalar. At what points on the lines should they reach, so that the distance between them is the shortest? Find the shortest possible distance between them.
Solution:
Given, \(\vec{r}=(\hat{j}+2\hat{k})+\lambda(\hat{i}+2\hat{j}+3\hat{k})\)
The coordinates of a general point on the given line are given by
\(\frac{x-0}{1}=\frac{y-1}{2}=\frac{z-2}{3}\) = λ
where λ is some real number.

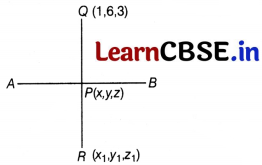
∴ x = λ, y = 2λ + 1, z = 3λ + 2

Let Q(1, 6, 3) be the given point and let P(x, y, z) be a point on the given line AB such that QP ⊥ AB.
Also, let R(x ₁ , y ₁ , z ₁ ) be the image of Q(1, 6, 3).
∴ The coordinates of P are (λ, 2λ + 1, 3λ + 2)
Direction ratios of QP are λ – 1, 2λ – 5, 3λ – 1
Direction ratios of given line are 1,2 and 3.
∴ (λ – 1)1 + (2λ – 5)2 + (3λ – 1)3 = 0 [∵ QP ⊥ AB]
⇒ λ – 1 + 4λ – 10 + 9λ – 3 = 0 ⇒ λ = 1
So, coordinates of P are (1, 3, 5). (1)
Now, since P is the mid-point of QR.
∴ (\(\frac{x_1+1}{2},\frac{y_1+6}{2},\frac{z_1+3}{2}\)) = (1, 3, 5)
On comparing, we get
x ₁ = 1, y ₁ = 0 and z ₁ = 7
The coordinates of the image of the point (1,6, 3) ,w.r.t. the line AB = (1, 0, 7)
Now, the distance of the point (1, 0, 7) from Y-axis

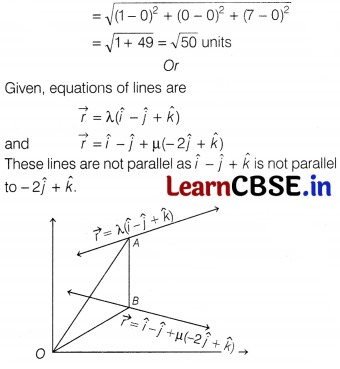
Let AB be the shortest distance between the lines such that AS makes right angle with both the lines.
Let the position vector of the point A lying on the line
\(\vec{r}=\lambda(\hat{i}-\hat{j}+\hat{k})\) ….(i)
and let the position vector of the point 6 lying on the line

⇒ 2 + 3µ – 3λ = 0 … (iii)
and 0(1 – λ) – 2(-1 – 2µ + λ) + 1(µ – λ) = 0
⇒ 2 + 5µ – 3λ = 0 … (iv)
From Eqs. (iii) and (iv),
2 + 3µ =2 + 5µ
⇒ 2µ =0
⇒ µ = 0
∴ λ = \(\frac{2}{3}\)

So, the position vector of the points at which they should be so that the distance between them is the shortest are

Section E
This section comprises of 3 case-study/passage-based questions of 4 marks each

Question 36.
Read the following passage and answer the questions given below.
In an office three employees James, Sophia and Oliver process incoming copies of a certain form. James processes 50% of the forms, Sophia processes 20% and Oliver the remaining 30% of the forms. James has an error rate of 0.06, Sophia has an error rate of 0.04 and Oliver has an error rate of 0.03.

Based on the above information, answer the following questions.
(i) Find the probability that Sophia processed the form and committed an error.
(ii) Find the total probability of committing an error in processing the form.
(iii) The manager of the Company wants to do a quality check. During inspection, he selects a form at random from the days output of processed form. If the form selected at random has an error, then find the probability that the form is not processed by James.
Or
Let E be the event of committing an error in processing the form and let E ₁ , E ₂ and E ₃ be the events that James,
Sophia and Oliver processed the form.

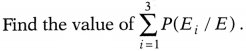
Solution:
Let E ₁ , E ₂ and E ₃ be the events that James, Sophia and Oliver processed the form, respectively.
Then, P(E ₁ ) = \(\frac{50}{100}=\frac{1}{2}\), P(E ₂ ) = \(\frac{20}{100}=\frac{1}{5}\)
and P(E ₃ ) = \(\frac{30}{100}=\frac{3}{10}\)
Let E be the event of committing an error.

(i) Probability that Sophia processed the form and committed an error
= P(E ∩ E ₂ )
= P(E ₂ ).P(E/E ₂ )
= \(\frac{1}{5}\) × 0.04
= 0.008

(ii) The total probability of committing an error
= P(E) = P(E ₁ ) – P(E/E ₁ ) + P(E ₂ )
P(E/E ₂ ) + P(E ₃ ) P(E/E ₃ )
= \(\frac{1}{2}\) × 0.06 + \(\frac{1}{5}\) × 0.04 + \(\frac{3}{10}\) × 0.03
= 0.047
[∵ P(E/E ₁ ) = 0.06, P(E/E ₂ ) = 0.04, P(E/E ₃ ) = 0.03]

(iii) The probability that the form is processed by James given that the form has an error

The probability that the form is not processed by James given that the form has an error

Question 37.
Read the following passage and answer the questions given below.
Teams A, B, C went for playing a tug of war game. Teams A, B, C have attached a rope to a metal ring and is trying to pull the ring into their own area.
Team A pulls with force F ₁ = \(6\hat{i}+0\hat{j}\) kN,
Team B pulls with force F ₂ = \(-4\hat{i}+4\hat{j}\) kN,
Team C pulls with force F ₃ = \(-3\hat{i}-3\hat{j}\) kN,

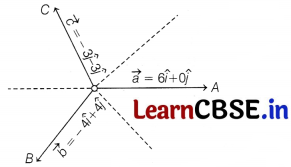
(i) What is the magnitude of the force of Team A?
(ii) Which team will win the game?
(iii) Find the magnitude of the resultant force exerted by the teams.
Or
In what direction is the ring getting pulled?
Solution:

(i) Magnitude of force of team A = |F ₁ | = 6 kN
(ii) Since, magnitude offeree of team A is greater than other teams, therefore team A will win the game.
(iii) Resultant force,

Or
Resultant force \(\vec{F}=-\hat{i}\hat{j}\)
Let \(\vec{F}\) makes an angle 6 with the X-axis, then its direction cosine along X-axis is cos θ.

Question 38.
Read the following passage and answer the questions given below.
The relation between the height of the plant (v in cm) with respect to its exposure to the sunlight is governed by the following equation y = 4x – \(\frac{1}{2}\)x²,
where x is the number of days exposed to the sunlight, for x ≤ 3.

(i) Find the rate of growth of the plant with respect to the number of days exposed to the sunlight.
(ii) Does the rate of growth of the plant increase or decrease in the first three days? What will be the height of the plant after 2 days?
Solution:
(i) Given, y = 4x – \(\frac{1}{2}\)x²
On differentiating w.r.t. x,
\(\frac{dy}{dx}\) = 4-x
∴ Rate of growth of the plant with respect to the number of days exposed to the sunlight is 4 – x.

(ii) \(\frac{dy}{dx}\) = 4 – x
On differentiating again w.r.t. x,
\(\frac{d^2y}{dx^2}\) = -1 < 0
⇒ \(\frac{dy}{dx}\)decreases
So, the rate of growth of the plant decreases for the first three days.
Height of the plant after 2 days
= y(2) = 4 × 2 – \(\frac{1}{2}\) × 2²
= 8 – 2 = 6cm