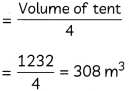Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths Standard Term 2 Set 2 with Solutions
Time Allowed: 2 Hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions
SECTION – A
(12 Marks)
Question 1.
If x = \(\frac{2}{3}\) and x = -3 are the roots of quadratic equation ax
2
+ 7x + b = 0, find the values of a and b.
OR
Solve for x:
\(\sqrt{2 x+9}+x=13\)
(2)
Answer:
Since, \(\frac{2}{3}\) and -3 are the roots of given quadratic equation,
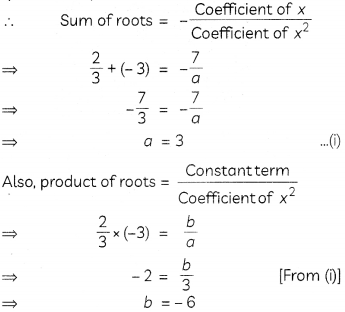
Hence, the respective values of a and b are 3 and -6.
OR
We have,
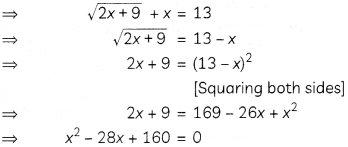
⇒ (x – 20) (x – 8) = 0
⇒ x = 20, 8
Hence, the values of x are 8 and 20.
Question 2.
The mean of eight numbers is 23. One more number is added to it. The new mean reduced to 22. Find the number added.
(2)
Answer:
Given: Mean of eight numbers = 23
Sum of eight numbers = 23 x 8
= 184
Let the newly added number be x.
Now, there are nine numbers in the set of data.
So, Sum of nine numbers = 184 + x
∴ Mean of nine numbers = \(\frac{184+x}{9}\)
But, mean of nine numbers = 22 [Given]
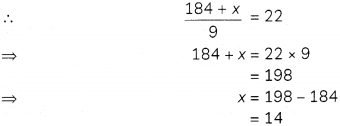
Hence, the number odded is 14.
Question 3.
In the given figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 40°. If AT is a tangent to the circle at point A, find ∠BAT.
(2)
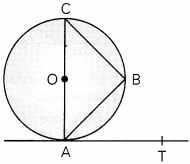
Answer:
Given: ∠ACB = 40°
Since, angle in a semi-circle is a right angle
∴ ∠ABC = 90°
So, in ΔABC
∠BAC = 180° – ∠ABC – ∠ACB
= 180° – 90° – 40°
= 50°
Now,
∠OAT = 90° [∵ Tangent! Radius]
⇒ ∠OAB + ∠BAT = 90°
⇒ 50° + ∠BAT = 90°
⇒ ∠BAT = 90° – 50° = 40°
Question 4.
Given below is a cumulative frequency distribution tabLe. Find the missing vaLues a, b, c and d.
| Class interval | Frequency | Cumulative Frequency |
| 0 – 10 | 17 | 17 |
| 10 – 20 | a | 45 |
| 20 – 30 | 32 | 77 |
| 30 – 40 | b | 101 |
| 40 – 50 | 19 | c |
| 50 – 60 | d | 130 |
Answer:
| Class interval | Frequency | Cumulative Frequency |
| 0 – 10 | 17 | 17 |
| 10 – 20 | a = 45 – 17 = 28 | 45 |
| 20 – 30 | 32 | 77 |
| 30 – 40 | b = 101 – 77 = 24 | 101 |
| 40 – 50 | 19 | c = 19 + 101 = 120 |
| 50 – 60 | d= 130 – 120 = 10 | 130 |
Concept Applied
The cumulative frequency of a doss is equaL to the sum of the frequency of the class arid the cumulative frequency of the preceding class.
Question 5.
The 19
th
term of an A.P. is equal to three times its sixth term. If its 9
th
term is 19, find the A.P.
(2)
Answer:
Let a be the first term and d be the common difference of the A.P.
Now, a
19
= 3a
6
⇒ a + 18 d = 3 (a + 5 d)
⇒ a + 18 d = 3 a + 15 d
⇒ 2a – 3d = 0 ………………………….. (i)
Also, a
9
= 19
⇒ a + 8d = 19 ………………………….. (ii)
Solving equations (i) and (ii), we get
a = 3, d = 2
So, the A.P. is 3, 5, 7, 9 …
Question 6.
If the total surface area of a solid hemisphere is 462 cm
2
, find its volume. \(\left[\text { Use } \pi=\frac{22}{7}\right]\)
OR
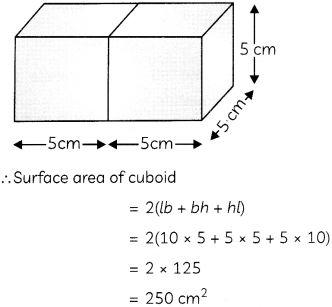
Rakesh, a student of cLass X, kept together two cubes, each of side 5 cm, to form a cuboid. Find the surface area of the cuboid so formed.
(2)
Answer:
Let the radius of the hemisphere be r cm.
Given: TSA of hemisphere = 462 cm
2
⇒ 3πr
2
= 462
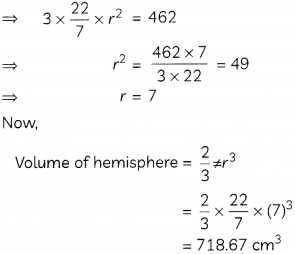
Related Theory
TSA of hemisphere = CSA of hemisphere + Area of base of hemisphere)
= 2πr
2
+ πr
2
= 3πr
2
OR
When two cubes of edge 5 cm each are joined together side by side, a cuboid is formed whose dimensions are 10 cm x 5 cm x 5 cm.
SECTION – B
(12 Marks)
Question 7.
The tops of two poles of heights 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with the horizontal, find the length of the wire.
(3)
Answer:
Let AB and CD be the two poles.
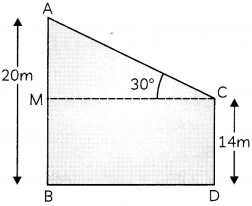
∴ AB = 20 m, CM = 14 m, and ∠ACM = 30°
So, AM = AB – MB
= AB – CD [∵ MB = CD]
= 20 – 14
= 6 m
Also, the wire joining the tops of two poles is AC.
So, in ΔAMC
sin 30° \(\frac{\mathrm{AM}}{\mathrm{AC}}\)
⇒ \(\frac{1}{2}=\frac{6}{A C}\)
⇒ AC = 12
Hence, the Length of the wire is 12 m.
Question 8.
Find two consecutive positive integers, sum of whose squares is 365.
(3)
Answer:
Let the two consecutive positive integers be x and (x + 1).
Then, according to the question
x
2
+ (x + 1)
2
= 365
⇒ 2x
2
+ 2x + 1 = 365
⇒ 2x
2
+ 2x – 364 =0
⇒ x
2
+ x – 182 = 0
⇒ (x + 14) (x – 13) = 0
⇒ x = -14, 13
Since, x is a positive integer,
x = 13
So, the two consecutive positive integers are 13 and 14.
Question 9.
Draw a circle of radius 2 cm with centre O and take a point P outside the circle such that OP = 6.5 cm. From P, construct two tangents to the circle.
(3)
Answer:
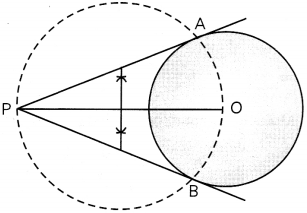
Steps of construction:
- Draw a circLe with centre 0 and radius 2 cm.
- Take a point P outside the circLe and join it to centre O such that OP = 6.5 cm.
- Draw perpendicuLar bisector of OP to get its mid-point M.
- Taking M as centre and OM = MP as radius, draw a circLe, intersecting the circLe drawn in step (1), at points A and B.
-
Join PA and PB.
Thus, PA and PB are the required tangents to the circLe with centre O.
Question 10.
Find the sum of all two-digit numbers which when divided by 7, leaves 2 as a remainder.
OR
Mala saved ₹ 10 in the first week of a year and then increased her weekly savings by ₹ 2. If in the nth week, her weekly savings is ₹ 68, then find the value of n. Also, find her weekly savings in 52
nd
week of the year.
(3)
Answer:
List of two-digit numbers which Leave remainder 2, when divided by 7 is:
(14 + 2), (21 + 2), (28 + 2) (91 + 2)
i.e. 16, 23, 30 ….. 93
This List of numbers forms an A.P. with a = 16, d = 7 and L = 93.
Let there be n terms in the A.P.
Then, L = a + (n – 1 )d
⇒ 93 = 16 + (n – 1) x 7
⇒ 7(n – 1) = 77
⇒ n – 1 = 11
⇒ n = 12
OR
Since, savings done by MaLa every week increases uniformLy by ₹ 2, so her savings form an A.P. with a = 10, d = 2 and a
n
= 68.
We know,
a
n
= a + (n – 1)d
⇒ 68 = 10 + (n – 1) x 2
⇒ 2(n – 1) = 58
⇒ n – 1 = 29
⇒ n = 30
So, the vaLue of n is 30.
Now,
a
52
= a + 51d
= 10 + 51 x 2
= 10 + 102
= 112
Hence, her savings in the 52
nd
week is ₹112.
Caution
In word problems, learn to differentiate savings in the nth week and total savings in n weeks. Otherwise, error could occur.
SECTION – C
(16 Marks)
Question 11.
If median of the following frequency distribution is 32.5, find the missing values f
1
and f
2
.
(4)
| Class Interval | Frequency |
| 0 – 10 | f 1 |
| 10 – 20 | 5 |
| 20 – 30 | 9 |
| 30 – 40 | 12 |
| 40 – 50 | f 2 |
| 50 – 60 | 3 |
| 60 – 70 | 2 |
| Total | 40 |
Answer:
| Class | Frequency | Cumulative Frequency |
| 0 – 10 | f 1 | f 1 |
| 10 – 20 | 5 | 5 + f 1 |
| 20 – 30 | 9 | 14 + f 1 |
| 30 – 40 | 12 | 26 + f 1 |
| 40 – 50 | f 2 | 26 + f 1 + f 2 |
| 50 – 60 | 3 | 29 + f 1 + f 2 |
| 60 – 70 | 2 | 31 + f 1 + f 2 |
| N = 40 |
We have,
Sum of frequencies = 40
∴ 31 + f
1
+ f
2
= 40
⇒ f
1
+ f
2
= 9 ……………………………. (i)
Now,
Median = 32.5 [Given]
∴ Median class = 30 – 40
We know,
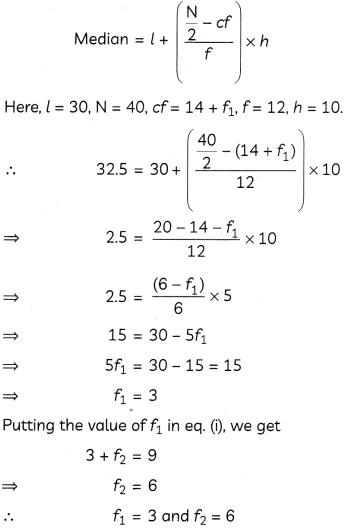
Question 12.
If the angles of elevation of the top of the candle from two coins distant a cm and b cm, (a > b), from its base and in the same straight line from it are 30° and 60°, respectively. Find the height of the candle.
OR
Two palm trees of equal heights are standing opposite to each other on either side of a river, which is 80 m wide. From a point O between them on the river, the angles of elevation of the top of the trees are 60° and 30°, respectively. Find the height of the trees and the distances of the point O from base of the trees.
(4)
Answer:
Let AB be the candle and P and Q be the positions of two coins such that coin Q is nearer to the candle.
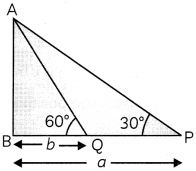
∴ ∠APB = 3O°, ∠AQB = 6O° BP = a, BQ = b.
Let height of the candle be h.
Now, in ΔABQ,

Caution
in the question, two constants namely. a and b, are given. So, the final answer must contain both the contents. Final answer, with one constant e.g. \(\sqrt{3} b\) or \(\frac{a}{\sqrt{3}}\) is incorrect.
OR
Let AB, CD be the two palm trees of equal heights.
∴ ∠OAB = 60°, ∠OCD = 30°, BD = 80m
Let BO = xm, and AB = CD = hm
Then, OD = BD – OB
= (80 – x) m
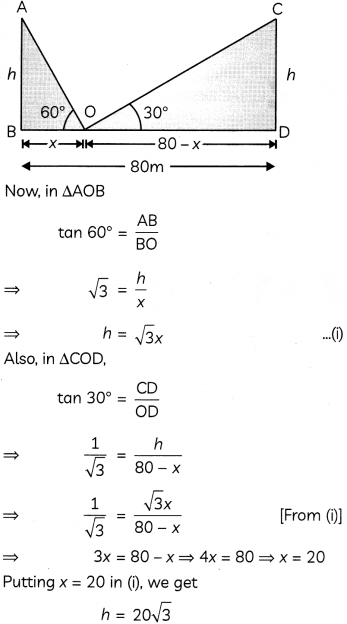
Hence, height of the trees is 20\(\sqrt{3}\) m each and distances of the trees from the point O are 20 m and (80 – 20)m, i.e. 60 m.
Question 13.
Case Study-1
A fountain is a decorative reservoir or a structure that jets water into the air for a decorative effect. Nowadays, LEDs of different colours are placed on their bases and by controlling the pressure of water, various dancing fountain shows are organized at different places.
In a society garden, a boundary was constructed around a circular fountain to restrict the children from playing with water.

Suppose the boundary was constructed in the shape of a quadrilateral ABCD, such that the walls AB, BC, CD and DA touches the fountain at points P, Q, R and S respectively.
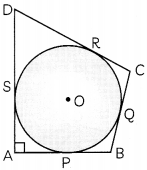
On the basis of above information, answer the following questions.
(A) If the LED
s
are placed along the boundaries of the four walls, then prove that AB + CD = BC + AD.
(2)
(B) Let O be the centre of the fountain and ∠PAS = 90°, prove that ASOP is a square.
(2)
Answer:
Case Study – 1
(A) We k.now, tangents drawn from an external point to a circle are equal in Length.
∴ AP = AS, BP = BQ, CR = CQ, DR = DS
Adding these equations, we get
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
Hence, proved.
(B) We have
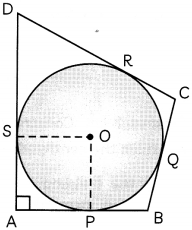
∠PAS = 90°
Also, AP = AS [From part (A)]
And, OS = OP [Radii]
So, in quadrilateral OPAS, adjacent sides are equal and an angle is a right angle.
∴ OPAS is a square.
Hence, proved.
Question 14.
Case Study-2
A tent is a shelter consisting of sheets of various materials draped over, attached to o frame of poles or attached to a supporting rope.

A student adventure camp of 3 dags was organized by the school for class X students. Their accommodation was organized in tents. A group of four students was to share a tent and they were asked to prepare their own tent. The teacher asked them to prepare a conical tent of radius 7 m and for this purpose, they were provided a canvas of area 551 m 2 in which 1 m 2 is used in stitching and wasted.
Based on the given information answer the following questions:
(A) Find the height of the tent.
(2)
(B) Find the amount of air required by each student in the tent.
(2)
Answer:
Case Study – 2
(A) Let L h be the slant height and height of the tent, respectively.
Since, 1m2 of canvas is wasted in stitching
∴ Total canvas present in tent
= 551 – 1 = 550m
2
Now, total canvas present in tent
= CSA of tent
= CSAofcone
= πrl
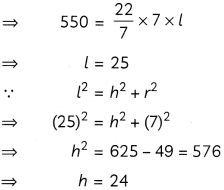
Hence, height of the tent is 24 m.
(B) Amount of air in = Volume of the tent the tent
= Volume of come
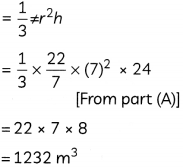
Since, each tent is shared by 4 sutdents,
∴ Amount of air required by each tent