CBSE Sample Papers for Class 10 Maths Standard Set 9 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths with Solutions Set 9 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 9 with Solutions

Time: 3 hrs
Max. Marks: 80

Instructions

1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
(Section A consists of 20 questions of 1 mark each.)

Question 1.
If \(\sqrt{3}\)tanθ = 3sinθ. Then, the value of sin ² θ – cos ² θ is (1)
(a) 3
(b) 1
(c) \(\frac{1}{3}\)
(d) \(\sqrt{3}\)
Answer:
(c) \(\frac{1}{3}\)

Question 2.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°, respectively. If the bridge is at a height of 9 m from the surface of river, then find the width of the river.
(a) 23 m
(b) 25 m
(c) 27 m
(d) 29 m
Answer:
(b) 25 m
Explanation: Here, width of the river = DC

In Δ ABC,
tan 30° = \(\frac{\mathrm{AB}}{\mathrm{BC}}\)
⇒ BC = \(\frac{9}{\tan 30^{\circ}}\) = 9√3 m
Now, in Δ ABD , AB
tan 45° = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ 1 = \(\frac{\mathrm{AB}}{\mathrm{BD}}\)
⇒ AB = BD
⇒ BD = 9m
Hence, DC = DB + BC = 9 + 9√3 [√3 = 1.732]
= 9(√3 + 1)
= 9(1.732 + 1)
= 9 × 2.732
= 24.588 m
≅ 25 m.

Question 3.
If a pair of linear equations in two variables is consistent, then the lines represented by two equations are (1)
(a) perpendicular
(b) coincident
(c) neither coincident nor perpendicular
(d) None of the above
Answer:
(b) coincident

If a pair of linear equations in two variables is consistent, then the lines represented by two equations are coincident.

Question 4.
In the given fig., two line segments, AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then ZPBA is equal to:

(a) 30°
(b) 60°
(c) 80°
(d) 100°
Answer:
(d) 100°
Explanation: In ΔAPB and ΔCPD,
∠APB = ∠CPD = 50° [vertically opposite angles]
\(\frac{\mathrm{AP}}{\mathrm{PD}}\) = \(\frac{6}{5}\) …….. (i)
and \(\frac{\mathrm{BP}}{\mathrm{CP}}\) = \(\frac{3}{2.5}\) = \(\frac{6}{5}\) ……..(ii)
From equations (i) and (ii),
\(\frac{\mathrm{AP}}{\mathrm{PD}}\) = \(\frac{\mathrm{BP}}{\mathrm{CP}}\)
∴ ΔAPB ~ ΔCPD [by SAS similarity criterion]
∴ ∠A = ∠D = 30° [corresponding angles of similar triangles]
In ΔAPB,
∠A + ∠B + ∠APB = 180° [sum of angles of a triangle = 180°]
⇒ 30° + ∠B + 50° = 180°
∴ ∠B = 180° – (50° + 30°)
= 100°
i.e., ∴ PBA = 100°.

Question 5.
The value of k, for which one root of the quadratic equation kx ² – 14x + 8 = 0 is six times the other, is (1)
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(d) 3

Let a and 6a be the roots of the quadratic equation kx ² -14x + 8 = 0, then Sum of roots,
α + 6α = –\(\left(\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\right)\) = \(\frac{-(-14)}{k}\)
⇒ 7α = \(\frac{14}{k}\) ⇒ α = \(\frac{2}{k}\) ……….(i)
and product of roots
α × 6α = –\(\left(\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\right)\) = \(\frac{8}{k}\)
⇒ 6α ² = \(\frac{8}{k}\) ….. (ii)
From Eqs. (i) and (ii), we get
6\(\left(\frac{2}{k}\right)^3\) = \(\frac{8}{k}\) ⇒ \(\frac{6 \times 4}{k^2}\) = \(\frac{8}{k}\)
k = \(\frac{24}{8}\) = 3

Question 6.
A solid right-circular cone is cut into two parts at the middle of its height by a plane parallel to its base. The ratio of the volume of the smaller cone to the whole cone is:
(a) 1 : 2
(b) 1 : 4
(c) 1 : 6
(d) 1 : 8
Answer:
(d) 1 : 8 cm
Explanation: Let the height of the bigger cone be 2x cm.
Thus, height of the smaller cone = x cm
Also let the radius of the larger cone be 2r cm.
Thus, radius of the smaller cone = r cm (by mid-point theorem)
Now, volume of the large cone
V = \(\frac{1}{3}\) × π(2r) ² (2x) = \(\frac{8 \pi}{3}\)r ² x
and volume of the smaller cone = \(\frac{1}{3}\) π(r) ² (x)
\(\frac{\pi}{3}\)r ² x
Thus, \(\frac{\text { Volume of the smaller cone }}{\text { Volume of the larger cone }}=\frac{\frac{\pi}{3} r^2 x}{\frac{8 \pi}{3} r^2 x}\) = \(\frac{1}{8}\)

Question 7.
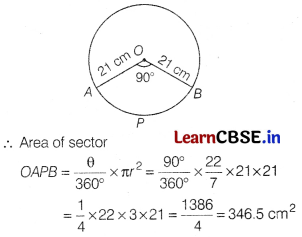
The area of a sector of circle of radius 21 cm and central angle 90° is (1)
[take π = \(\frac{22}{7}\)]
(a) 346.5 cm ²
(b) 340 cm ²
(c) 341.5 cm ²
(d) None of these
Answer:
(a) 346.5 cm ²

Let O be the centre of the circe of radius 21 cm such that \(\widehat{A P B}\) subtends 90° at the centre.

Question 8.
A pendulum swings through an angle of 30° and describes an arc 6.6 cm in length then the length of pendulum is:
(a) 12.6 cm
(b) 10.6 cm
(c) 5 cm
(d) 10 cm
Answer:
(a) 12.6 cm
Explanation:

Let r be the length of pendulum length of arc = 6.6 cm
∠AOB = 30°
Length of an arc = \(\frac{\theta}{360^{\circ}}\) × 2πr
⇒ 6.6 = \(\frac{30^{\circ}}{360^{\circ}}\) × 2 × \(\frac{22}{7}\) × r
⇒ r = \(\frac{6.6 \times 360 \times 7}{2 \times 30 \times 22}\)
= \(\frac{6.6 \times 12 \times 7}{44}\) = \(\frac{6 \times 12 \times 7}{40}\)
r = 12.6 cm

Question 9.
It is given that ΔABC ~ ΔDFE, ∠A = 50°, ∠C = 30°, AB = 10 cm, AC = 15 cm and DF = 8 cm. Then, which of the following is true? (1)
(a) DE = 12 cm and ∠F = 50°
(b) DE = 12 cm and ∠F = 100°
(c) EF = 12 cm and ∠D = 100°
(d) EF = 12 cm and ∠D = 30°
Answer:
(b) DE = 12 cm and ∠F = 100°

Given, ΔABC ~ ΔDFE

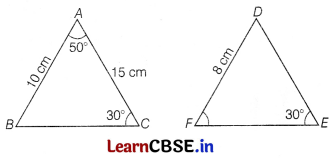
Then, ∠A = ∠D = 50°
∠C = ∠E = 30°
∴ ∠B = ∠F = 180° – (30° + 50°) = 100°
Also, \(\frac{A B}{D F}\) = \(\frac{A C}{D E}\)
⇒ \(\frac{10}{8}\) = \(\frac{15}{D E}\)
⇒ DE = \(\frac{15 \times 8}{10}\) = 12 cm
Hence, DE = 12 cm and ∠F = 100°

Question 10.
Find the roots of the quadratic equation 2x ² + x – 1 = 0.
(a) -1 and \(\frac{1}{2}\)
(b) 1 and –\(\frac{1}{2}\)
(c) 2 and \(\frac{1}{2}\)
(d) 1 and 2
Answer:
(a) -1 and \(\frac{1}{2}\)
Explanation: Given, 2x ² + x – 1 = 0
⇒ 2x ² + 2x – x – 1 = 0
⇒ 2x (x + 1) – 1 (x + 1) = 0
⇒ (x + 1)(2x – 1) = 0
⇒ x = -1 or x = \(\frac{1}{2}\)
Hence roots of equation are – 1 and \(\frac{1}{2}\).

Question 11.
Two poles of height 6 m and 11 m stand vertically upright on a plane ground. If the distance between their foot is 12 m, then the distance between their tops is (1)
(a) 14 m
(b) 16 m
(c) 13 m
(d) 15 m
Answer:
(c) 13 m

Let AB and CD be the vertical poles.
AB = 6 m, CD = 11 m and AC = 12 m

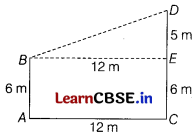
Draw BE || AC,
DE = (CD – CE) = (11 – 6)m = 5 m
In rightangled ΔBED, using Pythagoras theorem,
(BD) ² = (BE) ² + (DE) ²
= 12 ² + 5 ² = 169
∴ BD = \(\sqrt{169}\)m = 13 m
Hence, distance between their tops = 13 m

Question 12.
What is the mean of the following data?

Class interval	Frequency
50 – 60	8
60 – 70	6
70 – 80	12
80 – 90	11
90 -100	13

(a) 78
(b) 68
(c) 48
(d) 58
Answer:
(a) 78
Explanation:

Class Interval	f	x	f × x
50 – 60	8	55	440
60 – 70	6	65	390
70 – 80	12	75	900
80 – 90	11	85	935
90 -100	13	95	1235
	Σf = 50		Σf i x i = 3900

Mean = \(\bar{x}=\frac{3900}{50}\) = 78

Question 13.
If the nth term of an AP is 3n – 8, then its 16th term is (1)
(a) 30
(b) 20
(c) 10
(d) 40
Answer:
(d) 40

Given, a _n = 3n – 8
∴ a ₁₆ = 3 × 16 – 8 = 48 – 8 = 40

Question 14.
If cosec θ – cot θ = \(\frac{1}{3}\), then find the value of cosec θ + cot θ.
(a) 3
(b) -3
(c) 1
(d) None of these
Answer:
(a) 3
Explanation: Given, cosec θ – cot θ = \(\frac{1}{3}\)
We know that cosec θ + cot θ = \(\frac{({cosec} \theta+\cot \theta) \times({cosec} \theta-\cot \theta)}{({cosec} \theta-\cot \theta)}\)
= \(\frac{{cosec}^2 \theta+\cot ^2 \theta}{{cosec} \theta-\cot \theta}\)
= \(\frac{1}{{cosec} \theta-\cot \theta}\)
⇒ cosec θ + cot θ = \(\frac{\frac{1}{1}}{\frac{1}{3}}\) = 3

Question 15.
C is the mid-point of PQ, if P is (4, x), C is (y, -1) and Q is (-2, 4), then x and y respectively are (1)
(a) – 6 and 1
(b) – 6 and 2
(c) 6 and – 1
(d) 6 and – 2
Answer:
(a) – 6 and 1

Given, C is the mid-point of PO i.e. P(4, x) and Q(-2, 4)

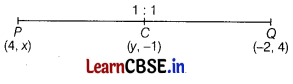
Therefore, (y, -1) = \(\left(\frac{4-2}{2}, \frac{x+4}{2}\right)\)
⇒ (y, -1) = (1, \(\frac{x+4}{2}\))
On equating the coordinates, we get
y = 1 and -1 = \(\frac{x+4}{2}\)
∴ x = -6 and y = 1

Question 16.
The ratio, in which point P(1, 2) divides the join of A(-2, 1) and B(7, 4), is [1]
(a) 1 : 2
(b) 2 : 1
(c) 2 : 2
(d) None of these
Answer:
(a) 1 : 2

Let the required ratio is k : 1.
Then, \(\frac{7 k-2}{k+1}\) =1 [by section formula]
⇒ 7k – 2 = k + 1 ⇒ 6k = 3 ∴ k = \(\frac{1}{2}\)
∴ Required ratio = 1 : 2

Question 17.
For grouped data, if Σf _i =20, Σf _i x _i = 2p + 20 and mean of distribution is 12, then the value of p is (1)
(a) 110
(b) 100
(c) 90
(d) 120
Answer:
(a) 110

Given, Σf _i = 20, Σf _i x _i = 2p + 20 and mean = 12
We know that
mean = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)
∴ 12 = \(\frac{2 p+20}{20}\)
⇒ 12 × 20 = 2p + 20
⇒ 240 = 2p + 20
⇒ 2p = 240 – 20
⇒ 2p = 220
⇒ p = \(\frac{220}{2}\) = 110

Question 18.
The system of equations 3x + y – 4 = 0 and 6x + 2y – 8 = 0 has :
(a) a unique solution x = 1, y = 1
(b) a unique solution x = 0, y = 4
(c) no solution
(d) infinite solution
Answer:
(d) infinite solution
Explanation: Given equation of system
3x + y = 4
and 6x + 2y = 8
Here, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}=\frac{1}{2}\)
Therefore, the system of equation has infinite solutions because it is a coincident line.

Directions In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) Points (3, 2), (-2, -3) and (2, 3) form a right triangle.
Reason (R) If (x, y) is equidistant from (3, 6) and (-3, 4), then 3x + y = 5. (1)
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Let A(3, 2), B(-2, -3) and C(2, 3).
∴ AB = \(\sqrt{(-2-3)^2+(-3-2)^2}\) = \(\sqrt{50}\) units
BC = \(\sqrt{(-2-2)^2+(-3-3)^2}\) = \(\sqrt{52}\) units and
CA = \(\sqrt{(2-3)^2+(3-2)^2}\) = \(\sqrt{2}\) units
∴ BC ² = AB ² + CA ²
⇒ ΔABC is a right triangle.
Let A'(3, 6), B'(-3, 4) and P (x, y)
Since, P is equidistant from A’ and B’.
∴ PA’ = PB’
⇒ PA’ ² = PB’ ²
⇒ (x – 3) ² + (y – 6) ² = (x + 3) ² + (y – 4) ²
⇒ x ² – 6x + 9 + y ² – 12y + 36 = x ² + 6x + 9 + y ² – 8y + 16
⇒ 12x + 4y = 20 ⇒ 3x+y = 5
Both Assertion (A) and Reason (R) are true but the Reason (R) is not correct explanation of Assertion – (A).

Question 20.
Statement A (Assertion): If f(x) is a quadratic expression such that f(1) + f(2) = 0. If – 1 is a root of f(x) = 0, then the other root is 8/5.
Statement R (Reason): If f(x) = ax ² + bx + c, then α + β = –\(\frac{b}{a}\) and αβ = \(\frac{c}{a}\)
Answer:
(b) Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Explanation: Given, f(1) + f(2) =0
For f(x) = ax ² + bx + c, we have
a + b + c + 4a + 2b + c = 0
=> 5a + 3b + 2c = 0 …… (1)
Since – 1 is a root of the equation
f(-1) = a – b + c = 0 ……. (2)
By eliminating c and b in turn by solving equations (1) and (2), we have
\(\frac{-b}{a}\) = \(\frac{3}{5}\), \(\frac{c}{a}\) = \(\frac{-8}{5}\)
Since – 1 is one root, the other root is \(\frac{8}{5}\).

Section B
(Section B consists of 5 questions of 2 marks each.)

Question 21.
If two tangents inclined at an angle of 60° are drawn to a circle of radius 5 cm, then find the length of each tangent. (2)
Answer:
In the given figure, OA = 5 cm and ∠APB = 60°

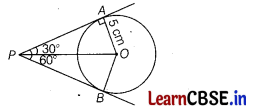
In ΔAOP, ∠PAO = 90°
[∵ the tangent at any point of a circle is perpendicular to the radius through the point of contact] (1)
Since, ∠APB = 60°
⇒ ∠APO = \(\frac{60^{\circ}}{2}\) = 30°
∴ tan 30° = \(\frac{A O}{A P}\) ⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{5}{A P}\)
⇒ AP = 5\(\sqrt{3}\) cm

Or

In the given figure, if the angle between two radii of a circle is 130°, then find the angle between the tangent at the ends of the radii.

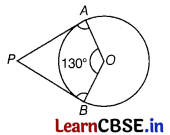
Answer:
From figure, ∠AOB = 130° ………. (i)
Clearly, ∠PAO = ∠PBO = 90° …….. (ii)
[∵ radius is perpendicular to the tangent at the point of contact]
Now, applying angle sum properly of quadrilateral in OAPB, we have
∠PAQ + ∠AOB + ∠OBP + ∠APB = 360°
90° + 130° + 90° + ∠APB = 360°
[from Eqs. (i) and (ii)]
∴ ∠APB = 360° – 310° = 50°
Hence, the angle between the tangent at the ends of the radii is 50°.

Question 22.
Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively.
OR
Express 23150 as product of its prime factors. Is it unique?
Solution:
It is given that on dividing 70 by the required number, there is a remainder 5. This means that 70 – 5 = 65 is exactly divisible by the required number.
Similarly, 125 – 8 = 117 is also exactly divisible by required number.
Now, required number = H.C.F. (65,117)

∴ 65 = 5 × 13
and 117 = 32 × 13
∴ H.C.F. (65,117) = 13
∴ Required number = 13
OR

Prime factors of 23150 = 2 × 5 × 5 × 463.
As per the fundamental theorem of Arithmetic, every number has a unique factorization.

Question 23.
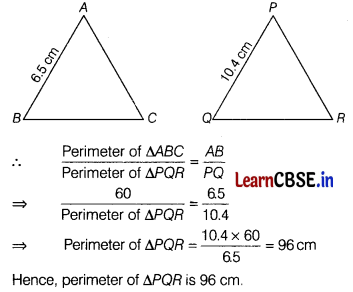
If ΔABC ~ ΔPQR, AB = 6.5 cm. PQ =10.4 cm and perimeter of ΔABC = 60 cm, then find the perimeter of ΔPQR. (2)
Answer:
Given, ΔABC ~ ΔPQR
We know that the ratio of the perimeter of two similar triangles is equal to the ratio of their corresponding sides.

Question 24.
For what value of k, the quadratic equation kx ² + 11x – 4 = 0 has real roots?
Solution:
Given quadratic equation is
kx ² + 11x – 4 = 0
On comparing with ax ² + bx + c = 0, we get
a = k, b = 11, c = -4
∵ It has real roots.
∴ D ≥ 0
⇒ b ² – 4ac ≥ 0
⇒ (11) ² – 4 × k × (- 4) ≥ 0
⇒ 121 + 16k ≥ 0
⇒ k ≥ \(\frac{-121}{16}\)

Question 25.
Find the sum of the series
7 + 10\(\frac{1}{2}\) + 14 + … + 84. (2)
Answer:
The given numbers are 7, 10\(\frac{1}{2}\), 14,………, 84.
∴ 10\(\frac{1}{2}\) – 7 = 14 – 10\(\frac{1}{2}\) = ……. = \(\frac{7}{2}\)
∴ The given numbers form an AP
Here, first term, a = 7,
common difference, d = 10\(\frac{1}{2}\) – 7 = 3\(\frac{1}{2}\) = \(\frac{7}{2}\)
and last term, l = a _n = 84
∵ a _n = a + (n – 1)d
∴ 84 = 7 + (n – 1)\(\frac{7}{2}\) [∵ a = 7 and d = \(\frac{7}{2}\)]
⇒ \(\frac{7}{2}\)(n – 1) = 84 – 7
⇒ \(\frac{7}{2}\)(n – 1) = 77
⇒ n – 1 = 77 × \(\frac{2}{7}\)
⇒ n – 1 = 22
⇒ n = 23
∵ Sum of n terms of an AR S _n = \(\frac{n}{2}\)(a + l)
∴ Sum of 23 terms (S ₂₃ ) = \(\frac{23}{2}\)(7 + 84)
= \(\frac{23}{2}\) × 91
= \(\frac{2093}{2}\) = 1046\(\frac{1}{2}\)

Or

Sarita saved ₹ 5 in the first week of the year and then increased her weekly savings by ₹ 1.75 each week. In which week will her weekly savings be ₹ 20.75? (2)
Answer:
Suppose, amount of weekly savings will be ₹ 20.75 in the nth week.
Amount of weekly savings form an AP with first term (a) = 5
and common difference (d) = 1.75
∵ nth term = 20.75
∴ a + (n – 1)d = 20.75 [∵ a _n = a + (n – 1)d]
⇒ 5 + (n – 1) × 1.75 = 20.75
⇒ (n – 1) × 1.75 = 20.75 – 5
⇒ (n – 1) × (1.75) = 15.75
⇒ n – 1 = \(\frac{15.75}{1.75}\)
⇒ n – 1 = 9
⇒ n = 10
Hence, Sarita’s weekly savings will be ₹ 20.75 in 10th week.

Section C
(Section C consists of 6 questions of 3 marks each.)

Question 26.
Find the point on the X-axis which is equidistant from the point (- 1, 0) and (5, 0).
Solution:
Given, A = (- 1, 0) and B = (5, 0).
Let the point on the X-axis be P(x, 0).
It is given that AP = PB
⇒ \(\sqrt{(x+1)^2+(0-0)^2}=\sqrt{(5-x)^2+(0-0)^2}[latex]
⇒ (x + 1) ² = (5 – x) ²
⇒ x + 1 = 5 – x
⇒ 2x = 4
⇒ x = 2
Thus, the point is (2, 0).

Question 27.
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO i.e. BO = 2 BC. (3)
Answer:
Two tangents BD and BC are drawn from an external point B.

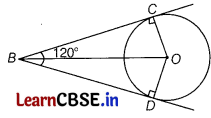
To prove BO = 2BC
Given, ∠DBC = 120°
Join OC, OD and BO.
Since, BC and BD are tangents.
∴ OC ⊥ BC and OD ⊥ BD
We know, OB is an angle bisector of ∠DBC.
∴ ∠OBC = ∠DBO = 60°
In right angled ΔOBC,
cos 60° = [latex]\frac{B C}{O B}\)
⇒ \(\frac{1}{2}\) = \(\frac{B C}{O B}\)
⇒ OB = 2BC
Also, BC = BD
[tangent drawn from external point to circle are equal]
OB = BC + BC
⇒ OB = BC + BD

Question 28.
A 5 m wide cloth is used to make a conical tent of base diameter 14 m and height 24 m. Find the cost of cloth used at the rate of ₹ 25 per m. [Use π = \(\frac{22}{7}\)]
OR
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. If the total surface area of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. [Use π = \(\frac{22}{7}\)]
Solution:
Given, Width of cloth = 5 m
Base diameter of tent = 14 m
∴ Radius = \(\frac{14}{2}\) = 7 cm 2
Height = 24 m
Slant height of cone, l = \(\sqrt{h^2+r^2}\)
= \(\sqrt{(24)^2+(7)^2}\)
= \(\sqrt{576+49}\)
= \(\sqrt{625}\)
= 25 cm
Let the length of the cloth be l’ m.
∴ Curved surface area of cone = Area of cloth
⇒ πrl = l’ × b
⇒ \(\frac{22}{7}\) × 7 × 25 = l’ × 5
⇒ 22 × 25 = l’ × 5
⇒ l’ = \(\frac{22 \times 25}{5}\)m
⇒ l’ = 110 m
Thus, total cost of the cloth = ₹(25 × 110) = ₹2750.
OR
Let the radius of base and height of a solid cylinder be r and h respectively.
Now, we have
r + h = 37 cm …….. (i)
and T.S.A. of solid cylinder = 2πr (r + h)
= 1628 cm ²
⇒ 2πr (37) = 1628 [Using(i)]
⇒ r = \(\frac{1628}{37 \times 2 \times \frac{22}{7}}\)
⇒ r = 7 cm
∴ Volume of the cylinder = πr ² h
= \(\frac{22}{7}\) × 7 × 7× 30 [Using eq. (i), h = 30]
= 4620 cm ³

Question 29.
If we add 1 to the numerator and subtract 1 from denominator, a function reduces to 1. It becomes \(\frac{1}{2}\) if we only add 1 to the denominator. What is the fraction? (3)
Answer:
Let x and y be the numerator and denominator of a fraction, respectively.
Then, the fraction = \(\frac{x}{y}\)
According to the question,
\(\frac{x+1}{y-1}\) = 1
⇒ x + 1 = y – 1
⇒ x – y = -2
⇒ -x + y = 2 …… (i)
and \(\frac{x}{y+1}\) = \(\frac{1}{2}\)
⇒ 2x = y + 1
⇒ 2x – y = 1 …… (ii)
On adding Eqs. (i) and (ii), we get
x = 3
From Eqs. (i), putting x = 3, we get
-3 + y = 2 ⇒ y = 5
Hence, the function is \(\frac{3}{5}\).

Question 30.
Find the mean of the following data :

Solution:
Given class interval is of inclusive form.
We have to convert it to exclusive form by subtracting 0.5 from lower limit and adding 0.5 to upper limit of each class interval.

Mean = A + \(\frac{\Sigma f_i u_i}{\Sigma f_i}\)
= 259.5 + \(\frac{-280}{36}\)
= 259.5 – 7.778
= 251.722

Question 31.
Find the points on the X-axis, which are at a distance of 2\(\sqrt{5}\) from the point (7, -4). How many such points are there? (3)
Answer:
At X-axis, y-coordinate is zero. So, let A (x, 0) be the point on X-axis, which is at a distance of 2\(\sqrt{5}\) from the point S (7, – 4).
AB = 2\(\sqrt{5}\)
⇒ \(\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}\) = 2\(\sqrt{5}\)
[by distance formula]
⇒ \(\sqrt{(x-7)^2+(0+4)^2}\) = 2\(\sqrt{5}\)
On squaring both sides, we get
(x – 7) ² + (0 + 4) ² = (2\(\sqrt{5}\)) ²
⇒ x ² + 49 – 14x + 16 = 20
[∵ (a – b) ² = a ² + b ² – 2ab]
⇒ x ² -14x + 65 – 20 = 0
⇒ x ² -14x + 45 = 0 (1)
⇒ x ² – 9x – 5x + 45 = 0 [by factorisation]
⇒ x(x – 9) – 5 (x – 9) = 0
⇒ (x – 9) (x – 5) = 0
x = 5 or 9
Hence, the required points are P ₁ (5, 0) and P ₂ (9, 0).
Also, note that we have only two such points.

Section D
(Section D consists of 4 questions of 5 marks each.)

Question 32.
(a) The third term of an A.P. is 7 and the seventh term exceeds three times the third term by 2. Find the first term, the common difference and the sum of first 20 terms.
(b) Find the sum of first seven numbers which are multiples of 2 as well as of 9.
Solution:
(a) Let a and d be the first term and common difference of given A.P. respectively.
Given: 3 ^rd term of A.P. = 7
⇒ T ₃ = 7
⇒ a + 2d = 7
and T ₇ – 3T ₃ = 2
⇒ T ₇ – 3 × 7 = 2
⇒ T ₇ = 2 + 21
⇒ T ₇ = 23
⇒ a + 6d = 23
Subtracting equation (ii) from (i), we get

Putting the value of d in equation (i), we get
a + 2 × 4 = 7
⇒ a = 7 – 8 = -1
Now, Sum of first 20 terms = \(\frac{20}{2}\) [2a + (20 – 1)d]
= 10 [2 × (- 1) + 19 × 4]
= 10 [- 2 + 76]
= 10 × 74 = 740

(b) Numbers which are multiples of 2 and 9 are
18, 36, 54, 72, 90, 108, 126,…
Since, 36 – 18 = 54 – 36 = 18
So, above series is an A.P. with a = 18, d = 18
Sum of first seven terms of the A.P. = \(\frac{7}{2}\) [2a + (7 – 1)d]
= \(\frac{7}{2}\) [2 × 18 + 6 × 18]
= \(\frac{7}{2}\) [36 + 108] = \(\frac{7}{2}\) × 144
= 7 × 72 = 504

Question 33.
The median of the following data is 16. Find the missing frequencies a and b, if the total of the frequencies is 70. (5)

Class	0-5	5-10	10-15	15-20	20-25	25-30	30-35	35-40
Frequency	12	a	12	15	b	6	6	4

Answer:
The cumulative frequency table is given below

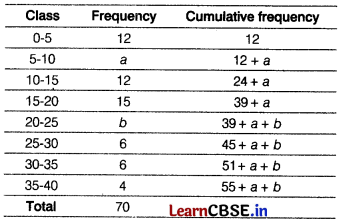
Here, 55 + a + b = 70
⇒ a + b = 70 – 55
⇒ a + b = 15 ……… (i)
Given, median of the data is 16, which lies in the interval 15-20.
Here, l = 15, cf = 24 + a, f = 15, h = 5
∴ Median = l + \(\frac{\frac{70}{2}-24-a}{15}\) × h
⇒ 16 = 15 + \(\frac{\frac{70}{2}-24-a}{15}\) × 5
⇒ 1 = (11 – a)/ 3
⇒ 11 – a = 3
⇒ a = 8 (1)
From Eq. (i), we get
8 + b = 15
⇒ b = 15 – 8 = 7

Question 34.
In the figure, ∠BED = ∠BDE and E divides BC in the ratio 2 : 1. Prove that AF × BE = 2 AD × CF.

The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{\mathrm{AO}}{\mathrm{OC}}\) = \(\frac{\mathrm{BO}}{\mathrm{OD}}\) . Show that ABCD is a trapezium.
Solution:
Since E divides BC in the ratio 2 : 1


OR

As there are only two parallel sides in this quadrilateral, it is a trapezium. Hence Proved.

Question 35.
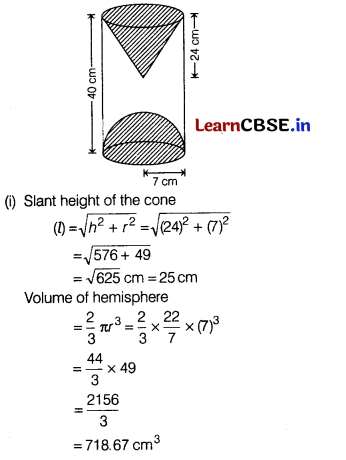
A wooden article was made by scooping out a hemisphere from one end of a cylinder and cone from the other end as shown in the figure. If the height of the cylinder is 40 cm, radius of the cylinder is 7 cm and height of the cone is 24 cm. (5)

(i) Find the slant height of the cone and the volume of hemisphere.
(ii) Find the total volume of the article.
Answer:
Given, height of the cylinder (H) = 40 cm
Radius of the cylinder (r) = 7 cm
Radius of the hemisphere (r) = 7 cm
Radius of the cone (r) = 7 cm
Height of the cone (h) = 24 cm

(ii) Volume of the article = Volume of the cylinder – Volume of the cone – Volume of the hemisphere

Or

A solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is 4 cm and the diameter of the base is 8 cm. If a right circular cylinder circumscribes the solid. Find, how much more space it will cover? (5)
Answer:
Let BPC be the hemisphere and ABC be the cone mounted on the base of the hemisphere.
Let EFGH be the right circular cylinder circumscribing the given toy.
We have, height of cone OA = 4 cm
Diameter of the base of the cone, d =8 cm

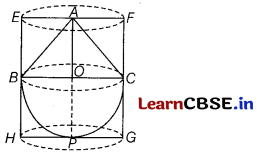
∴ Radius of the base of cone,
r = \(\frac{d}{2}\) = \(\frac{8}{2}\) = 4 cm
Here, AP = AO + OP
= 4 + 4 = 8 cm
Now, volume of the right circular cylinder = πr ² h
= π(4) ² × 8
= 128π cm ³
Volume of the solid toy = Volume of cone + Volume of hemisphere
= \(\frac{2}{3}\)πr ³ + \(\frac{1}{3}\)πr ² h
= \(\frac{2}{3}\)π × (4) ³ + \(\frac{1}{3}\)π(4) ² × 4
= \(\frac{128}{3}\)π + = \(\frac{64}{3}\)π
= \(\frac{192 \pi}{3}\)π
∴ Required space = Volume of the right circular cylinder – Volume of the toy
= 128π – \(\frac{192 \pi}{3}\)
= \(\frac{192 \pi}{3}\) cm ³
Hence, the right circular cylinder covers \(\frac{192 \pi}{3}\) cm ³ more space than the solid toy.

Section E
(Case Study Based Questions)
(Section E consists of 3 questions. All are compulsory.)

Question 36.
The given picture shows the position of an aeroplane, at 2 points A and B flying horizontally at a uniform speed of 20 m/sec. It is found that it takes the aeroplane 10 minutes to fly from A to B. The angle of elevation of A and B from a point P on the ground are 30° and 60° respectively.

Answer the following questions :
(i) How much distance does the aeroplane travels in 10 minutes?
(ii) How high is the aeroplane flying from the ground?
OR
Find the distance of PB.
(iii) Find the distance of AP.
Solution:
(i) Distance covered = Speed × Time
= 20 × 10 × 60 m
= 12,000 m
= 12 km

(ii) Let the height of the aeroplane from the ground be ‘h’ km

Then, tan 60° = \(\frac{h}{\mathrm{PQ}}\) ⇒ PQ = \(\frac{h}{\sqrt{3}}\)
and tan 30° = \(\frac{h}{\mathrm{PR}}\) ⇒ PR = √3h
But PR – PQ = QR = AB
⇒ √3h – \(\frac{h}{\sqrt{3}}\) = 12 km
⇒ 3h – h = 12√3
⇒ 2h = 12√3
⇒ h = 6√3 = 6 × 1.73 = 10.38 km
OR
In ΔPQB, sin 60° = \(\frac{\mathrm{BQ}}{\mathrm{PB}}\)
PB
⇒ \(\frac{\sqrt{3}}{2}=\frac{h}{\mathrm{~PB}}\) ⇒ \(\frac{\sqrt{3}}{2}=\frac{10.38}{\mathrm{~PB}}\)
⇒ PB = 12 km

(iii) Similarly, in ΔAPR
sin 30° = \(\frac{\mathrm{AR}}{\mathrm{AP}}\)
⇒ \(\frac{1}{2}\) = \(\frac{h}{\mathrm{AP}}\)
⇒ AP = 2 × 10.38
= 20.76 km

Question 37.
Play Cards
There are three friends and they want to play some interesting game. Firstly, they consider some cards and marked with the numbers 2 to 101 are placed in a box and mixed throughly. One card is drawn from this box.

Based on above information, answer the following questions.

(i) Find the probability that the drawn card is an even number. (1)
(ii) Find the probability that the drawn card is a number less than 14. (1)
(iii) Find the probability that the drawn card is a number which is a perfect square. (2)
Answer:
(i) There are 100 cards in the box out of which one card can be drawn in 100 ways.
∴ Total number of elementary events = 100
From numbers 2 to 101, there are 50 even numbers, namely, 2, 4, 6, 8,…… 100. Out of these 50 even numbered cards, one card can be chosen in 50 ways.
∴ Favourable number of elementary events = 50 Hence, P (getting an even number card)
= \(\frac{50}{100}\) = \(\frac{1}{2}\)

(ii) There are 12 cards bearing number less than 14, i.e. numbers 2, 3, 4, 5, …. 13.
∴ Favourable number of elementary events = 12
∴ P (getting a number less than 14)
= \(\frac{12}{100}\) = \(\frac{3}{25}\)

(iii) Those numbers from 2 to 101 which are perfect squares are 4, 9, 16, 25, 36, 49, 64, 81, 100, i.e. squares of 2, 3, 4, 5,…….. and 10 respectively.
Therefore, there are 9 cards marked with the numbers which are perfect squares.
∴ Favourable number of elementary events = 9
P(getting a number which is a perfect square) = \(\frac{9}{100}\)

Or

Find the probability that the drawn card is a prime number and it is less than 20. (2)
Answer:
Prime numbers less than 20 in the numbers from 2 to 101 are 2, 3, 5, 7, 11, 13, 17 and 19.
Thus, there are 8 cards marked with prime numbers less than 20. Out of these 8 cards one card can be choose in 8 ways.
∴ Favourable number of elementary events = 8
Hence, P (getting a prime number less than 20)
= \(\frac{8}{100}\) = \(\frac{2}{25}\)

Question 38.
Two hotels are at the ground level on either side of a mountain. On moving a certain distance towards the top of the mountain two huts are situated as shown in the figure. The ratio between the distance from hotel B to hut-2 and that of hut-2 to mountain top is 3 : 7.

(i) What is the ratio of the perimeters of the triangle formed by both hotels and mountain top to the triangle formed by both huts and mountain top?
(ii) If distance between hut-1 and mountain top is 10 miles, then find the distance between the hotel A and hut-1.
(iii) If the horizontal distance between the hut-1 and hut-2 is 8 miles, then find the distance between the two hotels is.
OR
If the distance from mountain top to hut-1 is 5 miles more than that of distance from hotel B to mountain top, then what is the distance between hut-2 and mountain top?
Solution:
(i) Let ΔABC is the triangle formed by both hotels and mountain top. ΔCDE is the triangle formed by both huts and mountain top.
Clearly DE || AB and so ΔABC ~ ΔDEC [By AA-similarity criterion]

Now, required ratio = Ratio of their corresponding sides = \(\frac{\mathrm{BC}}{\mathrm{EC}}\) = \(\frac{10}{7}\) i.e. 10 : 7.
(ii) Since, DE||AB, therefore
\(\frac{C D}{A D}=\frac{C E}{E B}\)
⇒ \(\frac{10}{\mathrm{AD}}=\frac{7}{3}\)
⇒ AD = \(\frac{10 \times 3}{7}\) = 4.29 miles.

(iii) Since,
ΔABC ~ ΔDEC
∴ \(\frac{B C}{E C}=\frac{A B}{D E}\) [∵ Corresponding sides of similar triangles
are proportional]
⇒ \(\frac{10}{7}=\frac{A B}{8}\)
⇒ AB = \(\frac{80}{7}\) = 11.43 miles
OR
Given, DC = 5 + BC
Clearly, BC = 10 – 5 = 5 miles
Now, CE =\(\frac{7}{10}\) × BC = \(\frac{7}{10}\) × 5 = 3.5 miles