CBSE Sample Papers for Class 10 Maths Standard Set 8 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Standard with Solutions Set 8 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 8 with Solutions

Time: 3 hrs
Max. Marks: 80

Instructions

1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
(Section A consists of 20 questions of 1 mark each.)

Question 1.
If (-1) ⁿ +(-1) ⁴ⁿ = 0, then n is [1]
(a) any positive
(b) any negative integer
(c) any odd natural number
(d) any even natural number
Answer:
(c) any odd natural number

(-1) ⁿ +(-1) ⁴ⁿ = 0 will be possible when n is any odd natural number.

Question 2.
In what ratio does the line x – y – 2 = 0 divides the line segment joining (3, -1) and (8, 9)?
(a) 3 : 3
(b) 2 : 3
(c) 3 : 2
(d) 3 : 4
Answer:
(b) 2 : 3
Explanation: Let P be the point that divides the line segment joining (3, -1) and (8, 9) in ratio k : 1.
Then, coordinates of point P is given by using internal section formula,
P(x, y) = [latex]\frac{8 k+3}{k+1}, \frac{9 k-1}{k+1}[/latex]
Since, point P lies on line x – y – 2 = 0, so P must satisfy the above equation.
Putting x = \(\frac{8 k+3}{k+1}\), y = \(\frac{9 k-1}{k+1}\) in equation x – y – 2 = 0, we get
\(\frac{8 k+3}{k+1}\) – (\(\frac{9 k-1}{k+1}\)) – 2 = 0
⇒ \(\frac{8 k+3-9 k+1-2 k-2}{k+1}\) = 0
⇒ \(\frac{-3 k+2}{k+1}\) = 0
⇒ – 3k + 2 = 0
⇒ k = \(\frac{2}{3}\)
⇒ k : 1 = \(\frac{2}{3}\) : 1 ⇒ 2 : 3
Hence, the required ratio is 2 : 3.

Question 3.
The ratio of the total surface area to the lateral surface area of a cylinder with base radius 80 cm and height 20 cm is [1]
(a) 1 : 2
(b) 2 : 1
(c) 3 : 1
(d) 5 : 1
Answer:
(d) 5 : 1

Given, radius of the base, r = 80 cm
and height of the cylinder h = 20 cm
∴ \(\frac{\text { Total surface area }}{\text { Lateral surface area }}\) = \(\frac{2 \pi r(h+r)}{2 \pi r h}\)
= \(\frac{h+r}{h}\) = \(\frac{20+80}{20}\)
= \(\frac{100}{20}\) = \(\frac{5}{1}\) = 5 : 1

Question 4.
In ΔABC, the angle bisector of ∠A cuts BC at E. Find the length of AC, if lengths of AB, BE and EC are 9 cm, 3.6 cm and 2.4 cm.
(a) 5.4 cm
(b) 8 cm
(c) 4.8 cm
(d) 6 cm
Answer:
(d) 6 cm
Explanation: In ΔABC, if AE is the angle bisector of ∠A, then according to the angle bisector theorem,

Question 5.
The ratio in which the line 3x + y – 9 = 0 divides the segment joining the points (1, 3) and (2, 7) is [1]
(a) 3 : 4
(b) 4 : 3
(c) 2 : 3
(d) 3 : 2
Answer:
(a) 3 : 4

Suppose the line 3x + y – 9 = 0 divides the line segment joining A(1, 3) and 6(2,7) in the ratio k : 1 at point C.
Then, coordinates of C are (\(\frac{2k+1}{k+1}\), \(\frac{7k+3}{k+1}\))
But C, lies on 3x + y – 9 = 0.
Therefore, 3(\(\frac{2k+1}{k+1}\)) + \(\frac{7k+3}{k+1}\) – 9 = 0
⇒ (6k + 3) + (7k + 3) – 9k – 9 = 0
⇒ 4k – 3 = 0
∴ k = \(\frac{3}{4}\)
So, the required ratio is 3 : 4 internally.

Question 6.
The length of arc of a sector of angle 0° of a circle with radius R is:
(a) \(\frac{2 \pi \mathrm{R} \theta}{180^{\circ}}\)
(b) \(\frac{2 \pi \mathrm{R} \theta}{360^{\circ}}\)
(c) \(\frac{\pi R^2 \theta}{180^{\circ}}\)
(d) \(\frac{\pi R^2 \theta}{360^{\circ}}\)
Answer:
(b) \(\frac{2 \pi \mathrm{R} \theta}{360^{\circ}}\)
Explanation: Length of arc of a sector = \(\frac{\theta}{360^{\circ}}\) × 2πR = \(\frac{2 \pi \mathrm{R} \theta}{360^{\circ}}\)

Question 7.
How many terms are there in the arithmetic series 1 + 3 + 5 + … + 73 + 75? [1]
(a) 28
(b) 30
(c) 36
(d) 38
Answer:
(d) 38

Given, the arithmetic series is
1 + 3 + 5 + …. + 73 + 75
Here, first term a = 1, common differenced = 2,

Last term = t _n = 75
Let number of terms in given series = n
Then, t _n = a + (n – 1)d
⇒ 75 = 1 + (n – 1) × 2
⇒ 75 = 1 + 2n – 2
⇒ 2n = 76
⇒ n = 38
Hence, there are 38 times in given series.

Question 8.
If triangle ABC is right angled at C, then find the value of cos (A + B).
(a) cos 60°
(c) cos 90°
(b) cos 30°
(d) cos 180°
Answer:
(c) cos 90°
Explanation: Given, ΔABC is right angled at C.
i.e., ∠C = 90°
Then by triangle angle sum property
∠A + ∠B + ∠C = 180°
⇒ ∠A + ∠B + 90° = 180°
⇒ ∠A + ∠B = 180° – 90°
⇒ ∠A + ∠B = 90°
Taking cos on both the sides, we get
cos (A + B) = cos 90°
cos (A + B) = 0 [∵ cos 90° = 0]

Question 9.
The pair of linear equations x + 2 y = 5 and 3x + 12y = 10 has [1]
(a) unique solution
(b) no solution
(c) more than two solutions
(d) infinitely many solutions
Answer:
(a) unique solution

The pair of linear equations are
x + 2y = 5 ⇒ x + 2y – 5 = 0
and 3x + 12y = 10 ⇒ 3x + 12y – 10 = 0
Here, a ₁ = 1, b ₁ = 2, c ₁ = -5
and a ₂ = 2, b ₂ = 12, c ₂ = -10
Now,
\(\frac{a_1}{a_2}=\frac{1}{3}\), \(\frac{b_1}{b_2}=\frac{2}{12}=\frac{1}{6}\)
As, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
So, pair of equations has unique solution.

Question 10.
Find the value of 9 sec ² A – 9 tan ² A.
(a) 8
(b) 10
(c) 9
(d) 7
Answer:
(c) 9
Explanation: We have
9 sec ² A – 9 tan ² A = 9(sec ² A – tan ² A)
= 9(1 + tan ² A – tan ² A)
= 9 × 1 [∵ sec ² θ = 1 + tan ² θ]
= 9

Question 11.
In the given figure, DE || BC and \(\frac{A D}{D B}=\frac{3}{5}\). If AC = 4.8 cm, then the length of AE is [1]
(a) 1.5 cm
(b) 1.8 cm
(c) 2 cm
(d) 4.2 cm
Answer:
(b) 1.8 cm

Let AE = x cm
Then, EC = (AC-AE)
= (4.8 – x)

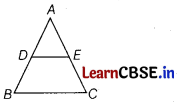
Now, in ∆ABC, DE || BC
\(\frac{A D}{D B}=\frac{A E}{E C}\)
\(\frac{3}{5}=\frac{x}{4.8-x}\)
3(4.8 – x) = 5x
8x = 14.4
x = 1.8
Hence, AE = 1.8 cm

Question 12.
ABC is a right angled triangle, right angled at B such that BC = 6 cm, AB = 8 cm and AC = 10 cm. A circle with centre O is inscribed in AABC. The radius of the circle is:
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Answer:
(b) 2 cm
Explanation: An incircle is drawn with centre O which touches the sides of the triangle ABC at P, Q and R. OP, OQ and OR are radii and AB, BC and CA are the tangents to the circle.
OP ⊥ AB, OQ ⊥ BC and OR ⊥ CA.
OPBQ is a square. (∴ ∠B = 90°)
Let r be the radius of the circle
∴ PB = BQ = r
AR = AP = 8 – r
CQ = CR = 6 – r
AC = AR + CR
10 = 8 – r + 6 – r
10 = 14 – 2r
2r = 14 – 10 = 4
r = 2
∴ Radius of the incircle = 2 cm.

Question 13.
The difference between the circumference and radius of a circle is 37 cm. The area of the circle is [1]
(a) 111 cm²
(a) 111 cm²
(c) 154 cm²
(d) 259 cm²
Answer:
(c) 154 cm²

Let R be the radius of the circle.
Given, 2πR – R = 37
R(2 × \(\frac{22}{7}\) – 1) = 37

R = 37 × \(\frac{7}{37}\) = 7 cm
Area of circle = πR² = (\(\frac{22}{7}\) × 7 × 7) = 154 cm²

Question 14.
Write the sum and product of the zeroes of the quadratic polynomial x ² + 7x + 10.
(a) 19, -8
(b) 13, 12
(c) -7, 10
(d) 11, -2
Answer:
(c) – 7, 10
Explanation: Given quadratic polynomial is x ² + 7x + 10
Here a = 1, b = 7 and c = 10
We know, sum of roots (α + β) = \(\frac{-b}{a}\)
α + β = \(\frac{-7}{1}\) = -7
Product of roots (αβ ) = \(\frac{c}{a}\)
αβ = \(\frac{10}{1}\) = 10

Question 15.
The sum of two numbers is 137 and their difference is 43. This situation can be algebraically represented as [1]
(a) x – y = 137, x + y = 180
(b) 2(x + y) = 137, 2(x – y) = 43
(c) x + y = 137, x – y = 43
(d) x + y = 43, x – y = 137
Answer:
(c) x + y = 137, x – y = 43

Let the two numbers be x and y, where x > y
Given, sum of numbers = 137
∴ x + y = 137
and difference of numbers = 43
∴ x – y = 43

Question 16.
A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder, in metres is:
(a) \(\frac{2}{\sqrt{3}}\)
(b) 2√3
(c) 2√2
(d) 4
Answer:
(d) 4
Explanation: Given, the distance of the ladder AC from the base of the wall AB is 2 m.

So, cos 60° = \(\frac{\mathrm{BC}}{\mathrm{AC}}=\frac{2}{x}\)
⇒ \(\frac{1}{2}=\frac{2}{x}\)
⇒ x = 2 × 2
The height of the ladder = 4 m.

Question 17.
If a and B are the zeroes of the polynomial f(x) = x² – p(x + 1) – c such that (α + 1)(β + 1) = 0, then c is equal to [1]
(a) 1
(b) 0
(c) -1
(d) 2
Answer:
(a) 1

Given, a and p are the zeroes of the polynomial
f(x) = x² – p(x + 1) – c
= x² – px – p – c = x – px – (p + c)

= -(P + c)
Now, it is given that (α + 1)(β + 1) = 0
⇒ αβ + α + β + 1 = 0
⇒ -(p + c) + p + 1 = 0
⇒ -c +1 = 0
∴ c = 1

Question 18.
What is the probability that two friends have different birthdays?
(a) \(\frac{1}{365}\)
(b) \(\frac{2}{365}\)
(c) \(\frac{364}{365}\)
(d)\(\frac{363}{365}\)
Answer:
(c) \(\frac{364}{365}\)
Explanation: If
Total number of possible outcomes = 365 × 365
Total number of favourable outcomes = 365 × (365 – 1)
= 365 × 364
∴ P(E) = \(\frac{365 \times 364}{365 \times 365}\) = \(\frac{364}{365}\)

Direction In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R) Circumference =2π × radius [1]
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true but Reason (R) is false
(d) Assertion (A) is false but Reason (R) is true
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)

C = 2 × \(\frac{22}{7}\) × r = 176
⇒ r = \(\frac{176 \times 7}{2 \times 22}\) = 28 cm
Both Assertion (A) and Reason (R) are true. Also, Reason (R) is the correct explanation of the Assertion (A).

Question 20.
Statement A (Assertion): In a cricket match a batsman hits a boundary 9 times out of 45 balls he plays. The probability that in a given throw he does not hit the boundary is 4/5.
Statement R (Reason): P(E) + P (not E) = 1.
Answer:
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
Explanation: For reason, as per the empirical formula
The sum of all the probabilities of all possible outcomes of experiment is 1.
P(Event) + P (not an Event) = 1
So, reason is true.
For assertion,
As per the description P(boundary) or P(E) = \(\frac{9}{45}\) = \(\frac{1}{5}\)
So P(no boundary) or P(not E) = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
So, assertion is also true and Reason is the correct explanation of the assertion.

Section B
(Section B consists of 5 questions of 2 marks each.)

Question 21.
In the following figures, CM and RN are respectively the medians of ∆ABC and ∆PQR.

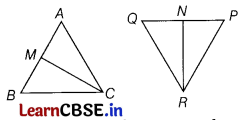
If ∆ABC ~ ∆PQR, then prove that ∆AMC ~ ∆PNR. [2]
Solution:
Given, ∆ABC ~ ∆PQR
\(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{C A}{P R}\)
[Y in similar triangles, corresponding sides are proportional]
and ∠A = ∠P, ∠B = ∠Q and ∠C = ∠R …(ii)
[v in similar triangles, corresponding angles are equal]
We know that the median bisects the opposite side.

Question 22.
Find a point on the Y-axis which is equidistant from the points A(-4, 3) and B(6, 5).
OR
The line segment joining the points A(3, -4) and B(1, 2) is trisected at the points P(p, – 2) and Q(\(\frac{5}{3}\), q).
Find the value of p and q.
Solution:
Let P be the required point on Y-axis.
∴ P = (0, y)
Now, PA = PB [Given]
∴ \(\sqrt{(0+4)^2+(y-3)^2}=\sqrt{(0-6)^2+(y-5)^2}\) [Using distance formula]
On squaring both sides,
(4) ² + (y – 3) ² = (6) ² + (y – 5) ²
⇒ 16 + y ² – 6y + 9 = 36 + y ² – 10y + 25
⇒ – 6y + 25 = 61 – 10y
⇒ – 6y + 10y = 61 – 25
⇒ 4y = 36
⇒ y = 9
∴ Coordinates of the point P = (0, 9)

OR

Question 23.
The length of minute hand of a clock is 14 cm. Then, find the area swept by the minute hand in one minute. [2]
Solution:
The minute hand of a clock describes a circle of radius equal to its length, i.e. 14 cm in 1 h. So, the angle described by minute hand in 60 min = 360°.
∴ Angle described by minute hand in
1 min = \(\frac{360°}{60°}\)= 6°
So, the area swept by the minute hand in
1 min is the area of a sector of angle 6? in a circle of radius 14 cm.
∴ Required area = \(\frac{\theta}{360^{\circ}} \times \pi r^2=\frac{6^{\circ}}{360^{\circ}} \times \frac{22}{7} \times(14)^2\)
= \(\frac{1}{60}\) × \(\frac{22}{7}\) × 14 × 14 = 10.27 cm²

Question 24.
Which term of the sequence 114, 109, 104, …………., is its first negative term?
OR
If the sum of the first n terms of an A.P. is given as S _n = n(4n + 1), then find its 6th term.
Solution:
Given sequence is 114, 109, 104, …….
Here, first term (a) = 114
Common difference (d) = 109 – 114 = – 5
Let nth term be the first negative term of the given A.P.
∴ a _n < 0
⇒ a + (n – 1)d < 0
⇒ 114 + (n – 1) (- 5) < 0
⇒ 114 – 5n + 5 < 0
⇒ 119 – 5n < 0
⇒ 119 < 5n ⇒ n > \(\frac{119}{5}\)
⇒ n > 23.8
∴ 24th term is the first negative term of the given A.P.
OR
Given : S _n = n (4n + 1)
So, Sn _{n – 1} = (n – 1){4(n – 1) + 1}
= (n – 1) (4n – 4 + 1)
= (n – 1) (4n – 3)
Now, nth term of A.P. is given as,
T _n = S _n – S _{n – 1}
= n(4n + 1) – (n – 1) (4n – 3)
= 4n ² + n – (4n ² – 3n – 4n + 3)
= 4n ² + n – 4n ² + 7n – 3
= 8n – 3
∴ T ₆ =8 (6) – 3
= 48 – 3 = 45

Question 25.
A line through the centre O of a circle of radius 5 cm cuts the tangent at a point P on the circle at Q such that OQ =13 cm. Find the length of PQ.
Or
In the given figure, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. If ∠QPR = 90°, then find the length of PQ.

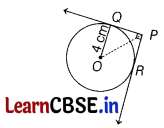
Solution:
We know that tangent at a point on a circle is perpendicular to the radius through = 144

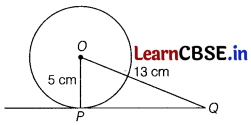
Therefore, OP is perpendicular to PQ.
In right angled ∆OPQ, we have
OQ ² = OP ² + PQ ² [by Pythagoras theorem]
⇒ PQ ² = OQ ² – OP ²
⇒ PQ ² = 13 ² – 5 ²
⇒ PQ ² = 169 – 25
⇒ PQ = 12 cm

Or

We know that if pair of tangents are drawn from an external point P, then line joining from centre O to the point P, bisects the angle P.

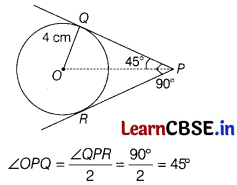
Also, radius of circle OQ is perpendicular to the tangent line QP.
Now, in right angled ∆OQP,
tan 45° = \(\frac{OQ}{QP}\)
⇒ 1 = \(\frac{4}{QP}\) [v OQ = 4 cm]
⇒ QP = 4cm
Hence, length of PQ is 4 cm.

Section C
(Section C consists of 6 questions of 3 marks each.)

Question 26.
Prove that 3 – √5 is an irrational number.
Solution:
Let us suppose that 3 – √5 is a rational number.
Then, it can be represented in \(\frac{p}{q}\) form i.e.,
3 – √5 = \(\frac{p}{q}\) [where p and q are real numbers and q ≠ 0]
⇒ 3 – \(\frac{p}{q}\) = √5
⇒ \(\frac{3 q-p}{q}\) = √5
∵ p and q are real numbers.
Therefore, \(\frac{3 q-p}{q}\) should also be a real number.
But we already know that √5 is an irrational number.
So, our assumption is wrong.
Hence, 3 – √5 is an irrational number. Hence Proved.

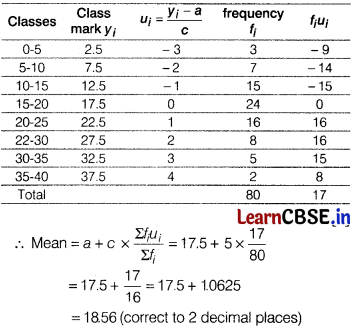
Question 27.
The following table gives marks scored by students in an examination

Marks	0-5	5-10	10-15	15-20	20-25	25-30	30-35	35-40
Number of Student	3	7	15	24	16	8	5	2

Calculate the mean mark correct to 2 decimal places.
Solution:
We shall use step-deviation method. Construct the table as under, taking assumed mean a = 17.5.
Here, c (width of each class) = 5

Question 28.
If α and β are the zeros of the quadratic polynomial f(x) = x ² – p(x + 1) – c, then show that (β + 1) (α + 1) = 1 – c.
Solution:
Given : The quadratic polynomial is f(x) = x ² – p(x + 1) – c = x ² – px – p – c
And α and β are the zeros of the given polynomial.
We know that, Sum of the zeros = – \(\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\)
Product of the zeros = \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\)
∴ α + β = – \(\frac{(-p)}{1}\)
α + β = p
and αβ = \(\frac{(-p-c)}{1}\)
αβ = – (p + c)
Now L.H.S. = (β + 1)(α + 1)
= αβ + (α + β) + 1
= – (p + c) + p + 1
= – p – c + p + 1
= 1 – c
= R.H.S.
Hense proved.

Question 29.
Given that the sum of the zeroes of the polynomial (a + 1)x ² + (2a + 3)x + (3a + 4) is -1 Find the product of its zeroes.
Or
If α, β, γ are the zeroes of the polynomial f(x) = ax ³ + bx ² + cx + d, then find the value of \(\frac{1}{α}\) + \(\frac{1}{β}\) + \(\frac{1}{γ}\). [3]
Solution:
Since, the sum of the zeroes of the quadratic polynomial (a + 1)x ² + (2a + 3)x + (3a + 4) is -1.
∴ \(\frac{-(2a+3)}{a+1}\) = -1

Or

Given, polynomial is ax ³ + bx ² + cx + d are α, β and γ.
Let P = \(\frac{1}{α}\) + \(\frac{1}{β}\) + \(\frac{1}{γ}\)
P = \(\frac{\beta \gamma+\gamma \alpha+\alpha \beta}{\alpha \beta \gamma}\)
∴ α β γ = \(\frac{-d}{a}\)
and α β + β γ + γ α = \(\frac{c}{a}\)
Now from Eq. (i) P = \(\frac{c / a}{-\frac{d}{a}}\) = \(-\frac{c}{a}\)

Question 30.
In ΔABC, DE || BC such that AD = (4x – 3) cm, AE = (8x – 7) cm, BD = (3x – 1) cm and CE = (5x – 3) cm. Find the value of x.
OR
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\)
Show that ABCD is a trapezium.
Solution:
In ΔABC, we have
DE || BC
So, \(\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}\) [Thales’ theorem]
⇒ \(\frac{4 x-3}{3 x-1}=\frac{8 x-7}{5 x-3}\)
⇒ (4x – 3)(5x – 3) = (8x – 7)(3x – 1)
⇒ 20x ² – 15x – 12x + 9 – 24x ² – 21x – 8x + 7
⇒ 4x ² – 2x – 2 = 0
⇒ 2x ² – x – 1 =0
⇒ 2x ² – 2x + x – 1 = 0
⇒ 2x(x – 1) + 1(x – 1) = 0
⇒ (x – 1)(2x + 1) = 0
⇒ x = 1 [as length cannot be negative]
So, the value of x = 1.

OR

Let EO || DC meet AD at E.
So, in ΔADC, EO || DC
So, \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{AE}}{\mathrm{ED}}\) [Thales’ theorem] ………… (i)
But \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{OD}}\) …….. (ii)
By (i) and (ii),
So, \(\frac{\mathrm{BO}}{\mathrm{OD}}=\frac{\mathrm{AE}}{\mathrm{ED}}\)
Hence, \(\frac{\mathrm{BO}}{\mathrm{OD}}=\frac{\mathrm{AE}}{\mathrm{ED}}\) and BO, OD, AE and ED are segments of ΔDAB.
So, EO || AB [By converse of Thales’ theorem]
But EO || DC
Thus, AB || DC
As there are only two parallel sides in this quadrilateral, it is a trapezium. Hence Proved.

Question 31.
Prove that

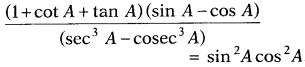
Solution:

Section D
(Section D consists of 4 questions of 5 marks each.)

Question 32.
Raju went to a Diwali funfair and stopped at a stall of spinning an arrow. Shopkeeper told him that arrow come to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 and these are equally likely outcomes.
(i) What is the probability that it will point at 8?
(ii) What is the probability that it will point at an odd number?
(iii) What is the probability that it will point at a prime number?
OR
FA piggy bank contains hundred 50 p coins, fifty ₹1 coins, twenty ₹2 coins and ten ₹5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, find the probability that the coin which fell (i) will be a 50p coin, (ii) will be of value more than ₹1, (iii) will be value less than ₹ 5, and (iv) will be a ₹1 or ₹2 coin.
Solution:
Total outcomes = {1, 2, 3, 4, 5, 6, 7, 8)
⇒ n (S) = 8
(i) Let A be the event that arrow will point at 8.
∴ A = {8}
⇒ n (A) = 1
∵ P (A) = \(\frac{1}{8}\)

(ii) Let B be the event that arrow will point at an odd number.
∴ B = {1, 3, 5, 7}
⇒ n( B) = 4
∴ P(B) = \(\frac{4}{8}\) = \(\frac{1}{2}\)

(iii) Let C be the event that arrow will point at a prime number.
∴ C = {2, 3, 5, 7}
⇒ n (C) = 4
∵ P(C) = \(\frac{4}{8}\) = \(\frac{1}{2}\)
OR
Total number of coins = (100 + 50 + 20 + 10) = 180
(i) Possible number of outcomes of a 50 p coin falling out = 100
Hence, P(E) = \(\frac{100}{180}\) = \(\frac{5}{9}\)

(ii) Possible number of outcomes of a coin falling out having value more than ₹1 = (20 + 10) = 30
Hence, P(E) = \(\frac{30}{180}\) = \(\frac{1}{6}\)

(iii) Possible number of outcomes of a coin falling out having value less than ₹5 = (100 + 50 + 20) = 170
Hence, P(E) = \(\frac{170}{180}\) = \(\frac{17}{18}\)

(iv) Possible number of outcomes of a coin falling out having value either ₹1 or ₹2 = (50 + 20) = 70
Hence, P(E) = \(\frac{70}{180}\) = \(\frac{7}{18}\)

Question 33.
Ram and Shyam together have 55 marbles. Both of them lost 5 marbles each and the product of the number of marbles they have is 164. Find out how many marbles they had to start with? [5]
Solution:
Given, Ram and Shyam together have 55 marbles. Let Ram has x marbles.
Then, number of marbles Shyam had = 55 – x
∵ Both of them lost 5 marbles each.
∴ The number of marbles Ram had = x – 5
and the number of marbles Shyam had = 55 – x – 5
= 50 – x
Now, product of the number of marbles = 164
⇒ (x – 5)(50 – x) = 164
⇒ 50x – x² – 250 + 5x = 164
⇒ -x² + 55x – 250 – 164 = 0
⇒ -x² + 55x – 414 = 0
⇒ x² – 55x + 414 = 0 [multiplying by (-1)]
which is the required quadratic equation.
Now, by factorisation method, we get
x² – 46x – 9x + 414 = 0
⇒ x(x – 46) – 9(x – 46) = 0
⇒ (x – 46)(x – 9) = 0
⇒ x – 46 = 0 or x -9 = 0
⇒ x = 46 or x = 9
When Ram has 46 marbles, then Shyam has = 55 – 46 = 9 marbles
When Ram has 9 marbles, then Shyam has = 55 – 9 = 46 marbles

Question 34.
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60°. Also find
the area of the corresponding major segment. [Use = π = \(\frac{22}{7}\)]
Solution:
Let ACB be the given arc subtending an angle of 60° at the centre.

Here, r = 14 cm and θ = 60°.
Area of the minor segment ACBA = (Area of the sector OACBO) – (Area of ΔOAB)
= \(\frac{\pi r^2 \theta}{360^{\circ}}\) – \(\frac{1}{2}\)r ² sin θ
= \(\frac{22}{7}\) × 14 × 14 \(\frac{60^{\circ}}{360^{\circ}}\) – \(\frac{1}{2}\) × 14 × 14 × sin 60°
= \(\frac{308}{3}\) – 7 × 14 × \(\frac{\sqrt{3}}{2}\) = \(\frac{308}{3}\) – 49√3 = 17.89 cm ²
Area of the major segment BDAB = Area of circle – Area of minor segment ACBA
= πr ² – 17.89
= \(\frac{22}{7}\) × 14 × 14 – 17.89
= 616 – 17.89 = 598.11 ≈ 598 cm ² .

Question 35.
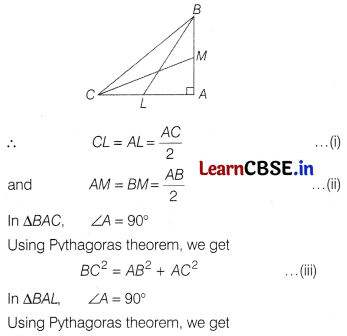
BL and CM are medians of ∆ABC right angled at A. Prove that
4(BL ² + CM ² ) = 5BC ² .
Solution:
In figure, ∠A = 90°. Since, BL and CM are medians, so the lines BL and CM divide AC and AB respectively, into two equal parts.

Section E
(Case Study Based Questions)
(Section E consists of 3 questions. All are compulsory.)

Question 36.
Mathematics teacher of a school took her 10 ^th standard students to show Red Fort. It was a part of their Educational trip. The teacher had interest in history as well. She narrated the facts of Red fort to students.
Then the teacher said in this monument one can find combination of solid figures. There are 2 pillars which are cylindrical in shape. Also 2 domes at the corners which are hemispherical 7 smaller domes at the centre.
Flag hoisting ceremony on Independence Day takes place near these domes.

(i) How much cloth material will be required to cover 2 big domes each of radius 2.5 metres? (Take π = 22 / 7)
(ii) Find the lateral surface area of two pillars if height of the pillar is 7m and radius of the base is 1.4 m is.
OR
The ratio of sum of volumes of two hemispheres of radius 1 cm each to the volume of a sphere of radius 2 cm?
(iii) The volume of a hemisphere if the radius of the base is 3.5 m.
Solution:
(i) Radius of a dome, r = 2.5 m
The dome is hemispherical in shape.
Then, Cloth material required = 2 × Surface area of hemisphere
= 2 × 2πr ²
= 4 × \(\frac{22}{7}\) × 2.5 × 2.5
= 78.57 m ²

(ii) Height of each pillar, h = 7 m
Radius of base, r = 1.4 m
Lateral surface area or curved surface area of 2 pillars = 2 × 2πrh
= 4 × \(\frac{22}{7}\) × 1.4 × 7
= 123.2 m ³
OR
Volume of 2 hemispheres of radius 1 cm
= 2 × \(\frac{2}{3}\)πr ³ = \(\frac{4}{3}\)π(1) ³
= \(\frac{4}{3}\)π cm ³
Volume of a sphere of radius 2 cm = \(\frac{4}{3}\)π(2) ³ = \(\frac{32}{3}\)π cm ³
Then, Required ratio = \(\frac{\frac{4}{3} \pi}{\frac{32}{3} \pi}=\frac{1}{8}\) = 1 : 8

(iii) Radius of hemisphere, r = 3.5 m
Then, volume of a hemisphere,
V = \(\frac{2}{3}\)πr ³ = \(\frac{2}{3}\) × \(\frac{22}{7}\) × (3.5) ³
= 89.83 m ³

Question 37.
A cyclist is climbing through a 20 m long rope which is highly stretched and tied from the top of a vertical pole to the ground as shown below

Based on the above information, answer the following questions
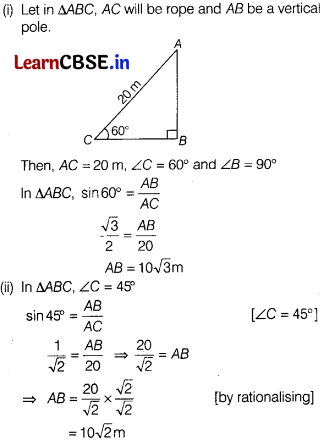
(i) Find the height of the pole, if angle made by rope with the ground level is 600. [1]
(ii) If the angle made by the rope with the ground level is 45°, then find the height of the pole. [2]
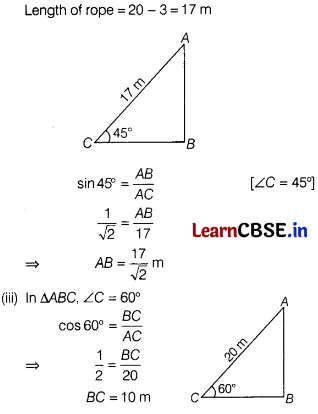
Or
If the angle made by the rope with the ground level is 450 and 3 m rope is broken, then what will be the height of the pole. [2]
(iii) If the angle made by the rope with the ground level is 600, then calculate the distance between artist and pole at ground level. [1]
Solution:

Or

Question 38.
One day, a poor girl is looking for a lamp-post to complete her homework as in her area power is not there and she finds the same at some distance away from her home. After completing the homework, she is walking away from the base of a lamp-post at a speed of 1.2 m/s. The lamp-post is 3.6 m above the ground and height of the girl is 90 cm (see figure).

(i) Find the distance of the girl from the base of the lamp-post after 4 seconds.
(ii) Find the length of her shadow after 4 seconds is.
OR
Find the ratio AC : CE is.
(iii) Sides of two similar triangles are in the ratio 9 : 16. The ratio of corresponding area of these triangles.
Solution:
(i) Let AB denote the lamp-post and CD be the girl after walking for 4 seconds away from the lamp-post.
Now, her distance from the base of the lamp
BD = 1.2 m × 4 = 4.8 m

(ii) ΔABE ~ ΔCDE
\(\frac{B E}{D E}=\frac{A B}{C D}\) (Let DE = x)
⇒ \(\frac{4.8+x}{x}=\frac{3.6}{0.9}\)
⇒ 4.8 + x = 4x
⇒ x = 1.6 m
So, the shadow of the girl after walking for 4 seconds.
OR
\(\frac{A E}{C E}=\frac{B E}{D E}\) = \(\frac{4.8+1.6}{1 \cdot 6}=\frac{6.4}{1 \cdot 6}\) = 4
⇒ AE = 4CE
⇒ AC + CE = 4CE
⇒ AC = 3CE ⇒ \(\frac{\mathrm{AC}}{\mathrm{CE}}=\frac{3}{1}\)

(iii) Since ratio of the area of two similar triangles is equal to the ratio of the square of their corresponding sides, Ratio of areas of similar triangles = (9) ² : (16) ² = 81 : 256.