Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Standard with Solutions Set 7 are designed as per the revised syllabus.
CBSE Sample Papers for Class 10 Maths Standard Set 7 with Solutions
Time: 3 hrs
Max. Marks: 80
Instructions
- This question paper has 5 Sections A-E.
- Section A has 20 MCQs carrying 1 mark each.
- Section B has 5 questions carrying 2 marks each.
- Section C has 6 questions carrying 3 marks each.
- Section D has 4 questions carrying 5 marks each.
- Section E has 3 Case Based integrated units of assessment (4 marks each).
- All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
- Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.
Section A
(Section A consists of 20 questions of 1 mark each.)
Question 1.
The HCF and LCM of two numbers are 33 and 264, respectively. When the first number is completely divided by 2, then the quotient is 33. The other number is [1]
(a) 66
(b) 130
(c) 132
(d) 196
Answer:
(c) 132
Given, HCF = 33 and LCM = 264
Let the other number be x.
First number =2 × 33=66
Product of numbers = HCF × LCM
∴ x × 66 = 33 × 264
⇒ x = \(\frac{33×264}{66}\) = 132
Question 2.
If the H.C.F. of two numbers is 1, then the two numbers are called :
(a) composite
(b) twin primes
(c) co-primes
(d) none of these
Answer:
(c) co-primes
Explanation: Two numbers are said to be co-primes if they have only one common factor, namely 1.
![]()
Question 3.
If the probability that it will rain tomorrow is 0.75, then the probability that it will not rain tomorrow is [1]
(a) 0
(b) 1
(c) 0.50
(d) 0.25
Answer:
(d) 0.25
We know that
P (tomorrow rain) + P (not tomorrow rain) = 1
⇒ 0.75 + P (not tomorrow rain) = 1
= P (not tomorrow rain) = 1 – 0.75 = 0.25
Hence, the probability that it will not tomorrow rain is 0.25.
Question 4.
For what value of k the system of equations x + 2y – 3 = 0 and 5x + ky + 7 = 0 has no solution?
(a) 10
(b) -10
(c) 2
(d) None of these
Answer:
(a) 10
Explanation: The given system of equation is
x + 2y – 3 = 0
5x + ky + 7 = 0
For no solution, we must have \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
Here, a
1
= 1 ,a
2
= 5, b
1
= 2, b
2
= k, c
1
= -3, c
2
= 7
\(\frac{a_1}{a_2}=\frac{b_1}{b_2}\)
⇒ \(\frac{1}{5}=\frac{2}{k}\)
⇒ K = 10
Now, \(\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
⇒ \(\frac{2}{10} \neq \frac{-3}{7}\)
Hence, for k = 10, the given system of equations has no solution.
Question 5.
If the difference of mode and median of a data is 24, then the difference of median and mean is
(a) 12
(b) 24
(c) 8
(d) 36
Answer:
(a) 12
We have, Mode – Median = 24
We know, Mode = 3 Median – 2 Mean
∴ Mode-Median = 2 Median – 2 Mean
⇒ 24 = 2(Median – Mean)
⇒ Median – Mean = 12
Question 6.
If α and β are the zeroes of a polynomial such that α + β = – 6 and αβ = -4, then write the polynomial:
(a) x
2
– 6x – 4 = 0
(b) x
2
+ 6x – 4 = 0
(c) x
2
+ 6x + 4 = 0
(d) x
2
– 6x + 4 = 0
Answer:
(b) x
2
+ 6x – 4 = 0
Explanation: Given α + β = -6
and αβ = -4
∵ The quadratic polynomial whose zeroes are α and β is given by
f(x) = x
2
– (α + β)x + aβ.
∴ The polynomial is f(x) = x
2
+ 6x – 4 = 0.
Question 7.
The perimeter of two similar triangles ∆ABC and ∆PQR are respectively, 48 cm and 36 cm. If PQ =12 cm, then the value of AB is
(a) 20 cm
(b) 16 cm
(c) 40 cm
(d) 25 cm
Answer:
(b) 16 cm
Given,
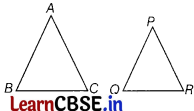
∆ABC ~ ∆PQR
∴ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\)
⇒ \(\frac{A B}{12}=\frac{48}{36}\)
∴ AB = 16 cm
Question 8.
If the value of cos A is \(\frac{4}{5}\), then what will be the value of tan A?
(a) \(\frac{4}{2}\)
(b) \(\frac{3}{4}\)
(c) \(\frac{5}{4}\)
(d) None of these
Answer:
(b) \(\frac{3}{4}\)
Explanation: Given, cos A = \(\frac{4}{5}\) = \(\frac{B}{H}\)
by Pythagoras theorem
Perpendicular = \(\sqrt{\mathrm{H}^2-\mathrm{B}^2}=\sqrt{(5)^2-(4)^2}=\sqrt{25-16}\) = √9 = 3
tan A = \(\frac{P}{B}\) \(\frac{3}{4}\)

Question 9.
From a solid circular cylinder with height 10 cm and radius of the base 6 cm, a right circular cone of the same height and same base is removed, then the volume of remaining solid is
(a) 280 π cm³
(b) 330 π cm³
(c) 240 π cm³
(d) 440 π cm³
Answer:
(c) 240 π cm³
Volume of the remaining solid
= Volume of the cylinder – Volume of the cone
= π × 6
2
× 10 – π × 6
2
× 10
= (360π – 120π ) = 240π cm³
![]()
Question 10.
The height of a tower is 12 m. Calculate the length of its shadow when the Sun’s altitude is 45°
(a) 12√3 m
(b) \(\frac{12}{\sqrt{3}}\)
(c) 12 m
(d) None of these
Answer:
(c) 12 m
Explanation: Let AB be the tower and AO be its shadow.
In Δ OAB tan 45 = \(\frac{\mathrm{AB}}{\mathrm{OA}}\)
⇒ 1 = \(\frac{\mathrm{AB}}{\mathrm{OA}}\)
⇒ OA = AB = 12 m
Hence, the length of shadow of the tower is 12 m.

Question 11.
If x = \(\frac{1}{2}\) is a root of the equation x² + kx – \(\frac{5}{4}\) = 0, then the value of k is [1]
(a) 3
(b) 0
(c) 1
(d) 2
Answer:
(d) 2
Since, x = \(\frac{1}{2}\) is a root of the equation
x² + kx – \(\frac{5}{4}\) = 0.
On putting x = \(\frac{1}{2}\) in the given equation, we get
(\(\frac{1}{2}\))
2
+ k(\(\frac{1}{2}\)) – \(\frac{5}{4}\) = 0
⇒ \(\frac{1}{4}\) + \(\frac{k}{2}\) – \(\frac{5}{4}\) = 0
⇒ \(\frac{k}{2}\) = \(\frac{5}{4}\) – \(\frac{1}{4}\)
⇒ k = 2(\(\frac{4}{4}\)) = 2.
Question 12.
The total surface area of a hemisphere of radius r is:
(a) πr
2
(b) 2πr
2
(c) 3πr
2
(d) \(\frac{1}{2}\)πr
2
Answer:
(c) 3πr
2
Explanation: Total area of hemisphere = Area of curved surface + Area of base
= 2πr
2
+ πr
2
= 3πr
2
Question 13.
tan²θ . sin²θ is equal to
(a) tan²θ – sin²θ
(b) tan²θ + sin²θ
(c) \(\frac{tan²θ}{sin²θ}\)
(d) sin²θ . cot²θ
Answer:
(a) tan²θ – sin²θ
We have, tan²θ . sin²θ

Question 14.
The length of the tangent from a point A at a distance of 5 cm from the centre of the circle is 4 cm. What will be the diameter of the circle?
(a) 6 cm
(b) 9 cm
(c) 5 cm
(d) 4 cm
Answer:
(a) 6 cm
Explanation: Given : OA = 5 cm and AB = 4 cm
In ΔOBA, ∠B = 90° [ ∵ Tangent to a circle makes 90° with the radius]
Therefore, by using Pythagoras theorem,
OA
2
= OB
2
+ AB
2
⇒ 5
2
= OB
2
+ 4
2
⇒ 25 – 16 = OB
2
⇒ OB = 3 cm
∴ Diameter of circle = 2 × OB = 6 cm

Question 15.
If PT is a tangent at T to a circle, where centre is O and OP =17 cm, OT = 8 cm, then the length of the tangent segment PT is
(a) 10 cm
(b) 20 cm
(c) 15 cm
(d) 25 cm
Answer:
(c) 15 cm
In right-angled ∆OTP,
OP
2
= OT
2
+ TP
2
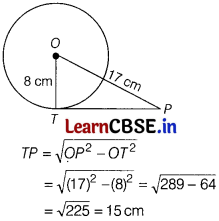
Hence, the length of tangent PT is 15 cm.
Question 16.
Find the value of k if the sum of the zeroes of the quadratic polynomial x
2
– (k + 6)x + 2(2k + 1) is half of their product.
(a) 7
(b) 4
(c) 5
(d) None of these
Answer:
(c) 5
Explanation: Given, the polynomial is x
2
– (k + 6)x + 2(2k + 1).
According to the question,
Sum of the zeroes = \(\frac{1}{2}\) Product of zeroes
We know, Sum of the zeroes = – \(\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}\) = – \(\frac{(-(k+6))}{1}\)
Product of the zeroes = \(\frac{\text { Constant term }}{\text { Coefficient of } x^2}\) = \(\frac{2(2 k+1)}{1}\)
∴ – \(\frac{\{-(k+6)\}}{1}\) = \(\frac{1}{2}\left\{\frac{2(2 k+1)}{1}\right\}\)
⇒ k + 6 = 2k + 1
⇒ 2k – k = 6 – 1
⇒ k = 5
Hence, the value of k is 5.
Question 17.
If in two triangles ∆DEF and ∆PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true? [1]
(a) \(\frac{E F}{P R}=\frac{D F}{P Q}\)
(b) \(\frac{D E}{Q R}=\frac{E F}{Q P}\)
(c) \(\frac{D E}{Q R}=\frac{D F}{P Q}\)
(d) \(\frac{E F}{R P}=\frac{D E}{Q R}\)
Answer:
(b) \(\frac{D E}{Q R}=\frac{E F}{Q P}\)
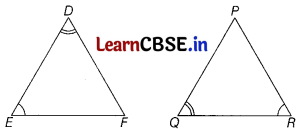
In ∆DEF and ∆PQR,
∠D = ∠Q
∠E = ∠R [given]
[from AA criterion]
∆DEF ~ ∆PQR
⇒ ∠F = ∠P [by CPCT]
∴ \(\frac{E D}{R Q}=\frac{F E}{P R}=\frac{D F}{Q P}\)
Hence, option (b) is not true.
Question 18.
A toy is in the form of a cone mounted on a hemisphere of a common base radius of 7 cm. If the total height of the toy is 31 cm, then the height of the cone is:
(a) 31 cm
(b) 38 cm
(c) 7 cm
(d) 24 cm
Solution:
(d) 24 cm
Explanation: Radius of hemisphere = Radius of cone = 7 cm
∴ Height of cone = Total height of toy – Radius of the sphere
= (31 – 7) cm
= 24 cm.

Directions In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.
Question 19.
Assertion (A) 5x² + 14x + 10 = 0 has no real roots.
Reason (R) ax² + bx + c = 0 has no real roots if b² < 4ac
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true but Reason (R) is false
(d) Assertion (A) is false but Reason (R) is true
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
Assertion (A) 5x² + 14x + 10 = 0
D = (14)
2
– 4.5.10 = 196 – 200 = – 4 < 0.
As, D < 0, no real roots.
Reason (R) True and it is of assertion correct explanation.
Question 20.
Statement A (Assertion): The area enclosed by a chord and the major arc is a major segment. Statement R (Reason): If a circle is divided into three equal arcs, then each is a major arc.
Answer:
(c) Assertion (A) is true, but reason (R) is false.
Explanation: For assertion, the area enclosed by a sector is proportional to the arc length of the sector.
So, A = \(\frac{\mathrm{RL}}{2}\) A = Area, R= Radius and L = Arc length.
Hence, the resulting enclosed area is a major segment if it is a major arc.
So the assertion is true.
For this reason, We denote an arc as a major arc when it is greater than the semicircle and if we divide a circle into 3 arcs each of them will be less than a semicircle so it is a minor arc.
Section B
(Section B consists of 5 questions of 2 marks each.)
Question 21.
In the given figure, if ∠RPS = 25°, then the value of ∠ROS.
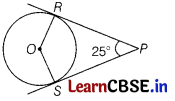
Solution:
Since, OR ⊥ PR and OS ⊥ SP
∠ORP = ∠OSP = 90°
In quadrilateral ORPS,
∠ROS + ∠ORP + ∠RPS + ∠OSP = 360°
⇒ ∠ROS + 90° + 25° + 90° = 360°
⇒ ∠ROS = 360° – 205 = 155°
![]()
Question 22.
D and E are points on sides AB and AC of triangle ABC such that DE || BC. If AD = 2.4 cm, DB = 3.6 cm and AC = 5 cm, find AE.
OR
In ΔDEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB.

Solution:
Given: DE || BC, AD = 2.4 cm, DB = 3.6 cm and AC = 5 cm
In ΔABC, DE || BC

⇒ 3AE = 10 – 2AE
⇒ 3AE + 2AE = 10
⇒ AE =
∴ AE = 2 cm
OR
Given AD = 4 cm, DE = 12 cm and DW = 24 cm.
Let DB = x cm
Since, BW = DW – BD
Then, BW = (24 – x) cm.
Similarly, AE = 12 – 4 = 8 cm
In DEW, AB || EW
∴ \(\frac{\mathrm{DA}}{\mathrm{AE}}=\frac{\mathrm{DB}}{\mathrm{BW}}\) [Thales’ theorem]
⇒ \(\frac{4}{12-4}=\frac{x}{24-x}\)
⇒ 8x = 96 – 4x
⇒ 12x = 96
⇒ x = \(\frac{96}{12}\) = 8
∴ DB = 8 cm
Question 23.
If cos θ – sin θ = √2 sin θ, then prove that find the cos θ + sin θ = √ cos θ.
Solution:
Given, cos θ – sin θ = √2 sin θ

Question 24.
Prove that \(\frac{2+\sqrt{3}}{5}\) is an irrational number, given that √3 is an irrational number. 2 + 73
Solution:
Let \(\frac{2+\sqrt{3}}{5}\) is a rational number.
∴ \(\frac{2+\sqrt{3}}{5}=\frac{a}{b}\) where a and b are co-prime numbers.
or 2 + √3 = \(\frac{5 a}{b}\)
⇒ √3 = \(\frac{5 a}{b}-\frac{2}{1}\)
⇒ √3 = \(\frac{5 a-2 b}{b}\)
In R.H.S., a, b, 2 and 5 are integers.
∴ R.H.S. is a rational number but given that √3 is an irrational.
So, it is a contradiction.
Hence, \(\frac{2+\sqrt{3}}{5}\) is an irrational number. Hence proved.
Question 25.
The short and long hands of a clock are 6 cm and 8 cm long, respectively. Then, find the sum of the distance travelled by their tips in 1 day. [take π = 22 /7]
Or
The radius of the wheel of a bus is 25 cm. If the speed of the bus is 33 km/h, then how many revolutions will the wheel make in 1 min?
Solution:
In 1 day i.e. 24 h, short (hour) hand of the clock make 2 revolutions and long (minute) hand make 24 revolutions.
In 1 revolution, distance travelled by tip of hour hand
= Circumference of circle of radius 6 cm
= 2 × \(\frac{22}{7}\) × 6
In 1 revolution distance travelled by tip of minute hand
= Circumference of circle of radius 8 cm
= 2 × \(\frac{22}{7}\) × 8
∴ Sum of distances travelled by tips of both hand in 1 day
= 2 × 2 × \(\frac{22}{7}\) × 6 + 24 × 2 × \(\frac{22}{7}\) × 8
= 2 × \(\frac{22}{7}\)(12 + 192)
= 2 × \(\frac{22}{7}\) × 204
= 1282.29 cm (approx).
Or
In 1 h, distance covered by wheel = 33 km
In 1 min, distance covered by wheel = \(\frac{33 \times 1000}{60}\) = 550 m
Now, number of revolutions made in 1 min
= \(\frac{\text { Distance covered by wheel }}{\text { Circumference of the wheel }}\)
= \(\frac{550}{2 \times \frac{22}{7} \times \frac{25}{100}}/latex] [∵ 25 cm = [latex]\frac{25}{100}\)m]
= \(\frac{550 \times 7 \times 100}{2 \times 22 \times 25}\) = 350
Section C
(Section C consists of 6 questions of 3 marks each.)
Question 26.
State whether the given pairs of triangles are similar or not. In case of similarity, mention the criterion.

Solution:
(i) \(\frac{\mathrm{AO}}{\mathrm{DO}}\) = \(\frac{16}{9}\) and \(\frac{\mathrm{BO}}{\mathrm{CO}}\) = \(\frac{9}{5}\)
∵ \(\frac{\mathrm{AO}}{\mathrm{DO}}\) ≠ \(\frac{\mathrm{BO}}{\mathrm{CO}}\)
∴ Given triangles are not similar.
(ii) In ΔPQR, ∠P + ∠Q + ∠R = 180° [Angle-sum property of a triangle]
⇒ 45° + 78° + ∠R = 180°
⇒ ∠R = 180° – 45° – 78° = 57°
In ΔLMN, ∠L + ∠M + ∠N = 180° [Angle-sum property of a triangle]
⇒ 57° + 45° + ∠N =180°
⇒ ∠N = 180° – 57° – 45°
= 78°
Now, in ΔPQR and ΔLMN
∠P = ∠M [Each 45°]
∠Q = ∠N [Each 78°]
∠R = ∠L [Each 57°]
By AAA similarity criterion
ΔPQR ~ ΔMNL
Question 27.
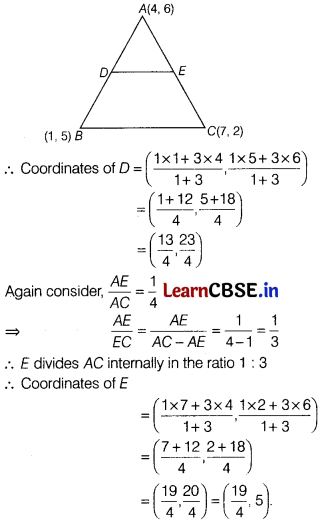
The vertices of ∆ABC are A (4, 6), 15(1, 5), and C(7, 2). A line is drawn to intersect sides AB and AC at D and E, respectively such that = \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{4}\). Determine the coordinates of D and E.
Solution:
Given,
\(\frac{A D}{A B}=\frac{1}{4}\) ⇒ \(\frac{A D}{A B}=\frac{A D}{AB-AD}\) = \(\frac{1}{4-1}\) = \(\frac{1}{3}\)
∴ D divides AB internally in the ratio 1 : 3
Question 28.
For what value of ‘p’ will the following pair of linear equations have infinitely many solutions :
px + 3y = p – 3,
12x + py = p
OR
Solve for x and y : 0.4x – 1.5y = 6.5 and 0.3x + 0.2y = 0.9.
Solution:
Given equations are, px + 3y = p – 3
and 12x + py =p
On comparing the given equations with a
1
x + b
1
y + c
1
= 0 and a
2
x + b
2
y + c
2
= 0, respectively, we get
a
1
= p; b
1
= 3; c
1
= – (p – 3)
a
2
= 12; b
2
= p; c
1
= -p
For infinitely many solutions,

⇒ p
2
= 36
⇒ p = ± 6
\(\frac{3}{p}=\frac{p-3}{p}\)
p
2
– 6p = 0
⇒ P(P – 6) = 0
⇒ p = 0 or p = 6
The above condition is satisfied, if p = 6
So, p = 6
OR
Given, 0.4x – 1.5y = 6.5
and 0.3x + 0.2y = 0.9
Multiplying given equations by 10, we get
4x – 15y = 65 …….. (i)
and 3x + 2y = 9 …….(ii)
Now, multiplying equation (i) with 2 and equation (ii) with 15, we get
8x – 30y = 130 …….. (iii)
and 45x + 30y = 135 ……. (iv)
Adding equations (iii) and (iv), we get
53x = 265
⇒ x = 5
Substituting x = 5 in equation (ii), we get
3(5)+ 2y = 9
⇒ 15 + 2y = 9
⇒ 2y = – 15 + 9
= -6
⇒ y = -3
Thus, x = 5 and y = -3.
![]()
Question 29.
In a trapezium, show that any line drawn parallel to the parallel sides of the trapezium divides the non-parallel sides proportionally.
Or
∆ABC is an isosceles triangle in which AB = AC = 10 cm and BC = 12 cm. PQRS is a rectangle inside the isosceles triangle. If PQ = SR = y cm, PS = QR = 2x, then prove that x = 6 – \(\frac{3y}{4}\).
Solution:
Given In trapezium ABCD,
AB || DC and EF || AB
To prove \(\frac{A E}{E D}=\frac{B F}{F C}\)
Construction Join AC to intersect EF at G.
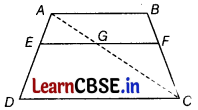
Proof Since, AB || DC and EF || AB
∴ EF || DC
[since lines parallel to the same line are also parallel to each other]
In ∆ADC,
EG || DC [∵EF || DC]
By using the basic proportionality theorem,
\(\frac{A E}{E D}=\frac{A G}{G C}\)
[by Thales theorem] …… (i)
In ∆ABC, GF || AB [∵ EF || AB]
By using the basic proportionality theorem,
\(\frac{C G}{A G}=\frac{C F}{B F}\) or \(\frac{A G}{G C}=\frac{B F}{C F}\)
[by Thales theorem] … (ii)
and taking the reciprocal of the terms]
From Eqs. (i) and (ii), we get
\(\frac{A E}{E D}=\frac{B F}{F C}\)
Hence proved.
OR
Given, AB = AC = 10 cm, BC = 12 cm and PORS is a rectangle in which PC = SR = y cm and PS = QR = 2x.

Question 30.
A bag contains 18 balls out of which, x balls are red. [3]
(i) If one ball is drawn at random from the bag, then what is the probability that it is the red ball?
Answer:
∵ Total number of balls in the bag = 18
Total number of red baUs in the bag = x
∴ P(drawing a red ball) = \(\frac{x}{18}\)
(ii) If 2 more red balls are put in the bag, then the probability of drawing a red ball will be 9/8 times that of the probability of a red ball coming in part (i). Find the value of x.
Answer:
∵ The number of red balls added to the bag = 2
∴ Total number of balls in the bag = 18 + 2 = 20
and total number of red balls in the bag = x + 2
Now, P (drawing a red ball) = \(\frac{x+2}{20}\)
According to the question,
\(\frac{x+2}{20}\) = \(\frac{9}{8}\left(\frac{x}{18}\right)\)
⇒ \(\frac{x+2}{20}\) = \(\frac{x}{16}\)
⇒ 16x + 32 = 20x
⇒ 4x = 32
∴ x = 8
Question 31.
If α and β are the zeroes of the quadratic polynomial f(x) = 3x² -4x + 1, then find a quadratic polynomial whose zeroes are
\(\frac{\alpha^2}{\beta}\) and \(\frac{\beta^2}{\alpha}\).
Solution:
Given that α and β are the zeroes of the polynomial
f(x) = 3x² -4x + 1
α + β = \(-\frac{\text { Coefficient of x }}{\text { Coefficient of x^2 }}\)
= \(-\frac{(-4)}{3}\) = \(\frac{4}{3}\)
and α . β = \(\frac{\text { Constant term }}{\text { Coefficient of x^2 }}\)
= \(\frac{1}{3}\)
Lets and P be sum and product of the zeroes of the
polynomial whose zeroes are \(\frac{\alpha^2}{\beta}\) and \(\frac{\beta^2}{\alpha}\).
Then,
S = \(\frac{\alpha^2}{\beta}\) + \(\frac{\beta^2}{\alpha}\) = \(\frac{\alpha^3+\beta^3}{\alpha\beta}\)

Section D
(Section D consists of 4 questions of 5 marks each.)
Question 32.
Find the mode of the following frequency distribution :

The table below gives the distribution of villages under different heights from sea level in a certain region. Find the mean height of the villages.
| Heights | No. of village |
| 200 | 142 |
| 600 | 265 |
| 1000 | 560 |
| 1400 | 271 |
| 1800 | 89 |
| 2200 | 16 |
Solution:
| Class | Frequency |
| 140 – 145 | 3 |
| 145 – 150 | 7f 0 |
| l 150 – 155 | 10f m |
| 155 – 160 | 7f 1 |
| 160 – 165 | 6 |
| 165 -170 | 1 |
| 170 – 175 | 3 |
Modal class = Class with highest frequency
= 150 – 155
Mode = l + \(\frac{f_m-f_0}{2 f_m-f_0-f_1}\) × h
Here, l = 150, f
m
= 10, f
1
= 7, f
0
= 7,h = 5
∴ Mode = 150 + \(\frac{10-7}{20-7-7}\) × 5
= 150 + \(\frac{3}{6}\) × 5
= 150 + 2.5 = 152.5
OR
Solution:
Compute the mean height of the region.
| Height (x i ) | No. of villages (f i ) | u i = \(\frac{x_i-\mathbf{A}}{h}\) | f i u i |
| 200 | 142 | -3 | -426 |
| 600 | 265 | -2 | -530 |
| 1000 | 560 | -1 | -560 |
| A = 1400 | 271 | 0 | 0 |
| 1800 | 89 | 1 | 89 |
| 2200 | 16 | 2 | 32 |
| Σf i = 1343 | Σf i u i = -1395 |
Here A = 1400, h = 400
We know that, Mean = A + \(\left\{\frac{\Sigma f_i u_i}{\Sigma f_i}\right\}\) × h
= 1400 + \(\frac{-1395}{1343}\) × 400
= 1400 – 415.49
= 984.51.
Question 33.
Find the missing frequencies in the following frequency distribution table, if n = 100 and median is 32.
Table 1
Solution:
Given, median = 32 and N = Σf
i
= 100
Let f
1
and f
2
be the frequencies of the class interval 10-20 and 40-50, respectively.
Since, sum of frequencies = 100
∴ 10 + f
1
+ 25 + 30 + f
2
+ 10 = 100
⇒ f
1
+ f
2
= 100 – 75
⇒ f
1
+ f
2
= 25
⇒ f
2
= 25 – f
1
…(i)
Now, the cumulative frequency table for given distribution is

Here, N = 100 ⇒ \(\frac{N}{2}\) = 50
Given, median = 32, which belongs to the class 30-40,
So, the median class is 30 – 40.
Then, l = 30, h = 10, f = 30 and cf = 35 + f
1
∵ \(\text { Median }=l+\left[\frac{\frac{N}{2}-cf}{f}\right] \times h\)
32 = 30 + \(\left\{\frac{50-35-f_1}{30}\right\}\) × 10
32 – 30 = \(\frac{15-f_1}{30}\) × 10
⇒ 2 × 3 = 15 – f
1
⇒ f
1
= 15 – 6 = 9
On putting the value of A, in Eq. (i), we get
f
2
= 25 – 9 = 16
‘Hence, the missing frequencies are f
1
= 9 and f
2
= 16.
Question 34.
Determine an A.P. whose 3
rd
term is 16 and when 5th term is subtracted from the 7th term, we get 12.
OR
Find the stun of all three-digit numbers which leave the remainder 3 when divided by 5.
Solution:
Let the first term of A.P. be a and common difference be d.
Given, a
3
= 16 and a
7
– a
5
= 12
So, a + 2d = 16 ………. (i)
and a + 6d – (a + 4d) = 12
⇒ a + 6d – a – 4d = 12
⇒ 2d = 12
∴ d = 6 ……… (ii)
Putting the value of d from equation (ii) in equation (i), we get
a + 2 × 6 = 16
⇒ a = 16 – 12
⇒ a = 4
Hence the required A.P. is : 4,10,16,22,…
OR
Smallest 3-digit number which leaves the remainder 3 when divided by 5 = 103
Greatest 3-digit number which leave the remainder 3 when divided by 5 = 998
Hence, the series is 103,108,113,118,…, 998
We observe that the above series is an A.P.
Where a – 103, d = 5, a
n
= 998
We know that, a
n
= a + (n- 1 )d
⇒ 998 = 103 + (n – 1) 5
⇒ 998 = 103 + 5n – 5
⇒ 998 = 98 + 5n
5 n = 998 – 98 = 900
n = 180
Now, S
n
= \(\frac{n}{2}\) [a + a
n
]
= \(\frac{180}{2}\) [103 + 998] = 90 × 1101 = 99090
Hence, sum of three-digit numbers which leave the remainder 3 when divided by 5 is 99090.
![]()
Question 35.
In an AP, the sum of m terms is equal to n and the sum of n terms is equal to m, then prove that the sum of (m + n) terms is -(m + n).
Or
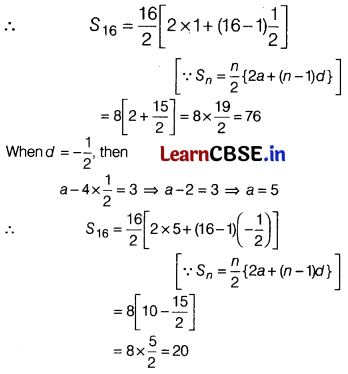
The sum of the third and seventh terms of an AP is 6 and their product is 8. Find the sum of first sixteen terms of an AP.
Solution:
Let a and d be the first term and common difference of an AP.
Then, S
m
= n
⇒ \(\frac{m}{2}\)[2a + (m – 1)d] = n
⇒ 2am + m(m – 1)d =2n …(i)
and S
n
= m
⇒ \(\frac{n}{2}\)[2a + (n -1)d] = m
⇒ 2an + n(n – 1)d = 2m …..(ii)
On subtracting Eq. (ii) from Eq. (i), we get
2a(m-n) + {m(m -1)-n(n -1)}d = 2n – 2m
⇒ 2a(m – n)+{m² – m – n² + n}d = 2(n – m)
⇒ 2a(m – n) + {m² – n² -(m – n)}d = -2(m – n)
⇒ (m -n) [2a + (m + n – 1)d] = -2(m – n)
[∵ a² – b² = (a + b)(a – b)]
⇒ [2a+(m + n – 1)d] = -2
[dividing both sides by (m – n)]
⇒ 2a + (m + n – 1)d = -2 …………(iii)
Now, S
m+n
= \(\frac{m+n}{2}\)[2a + (m + n – 1)d]
= \(\frac{m+n}{2}\)[-2] [from Eq. (iii)]
= -(m+n)
Hence proved.
Or
Let a and d be the f:rst term and common difference of an AP
Then, a
3
+ a
7
= 6 and a
3
a
7
= 8
⇒ a + (3 – 1)d+ a + (7 – 1)d = 6
and [a + (3-1)c/][a-ri7-iiry] = 8
[∵ a
n
= a + (n – 1)d]
⇒ a + 2d + a + 6d = 6
and [a + 2d][a + 6d] = 8
⇒ 2a + 8d = 6 and (a + 2d)(a+ 6d) = 8
⇒ a+ 4d = 3 and (a + 2d)(a + 6d) = 8
⇒ (3 – 4d + 2d )(3 – 4d + 6d) = 8
[∵ put a = 3 – 4d]
⇒ (3 – 2d)(3 + 2d) = 8
⇒ 9 – 4d² = 8
⇒ 4d² = 1
⇒ d² = \(\frac{1}{4}\)
d =±\(\frac{1}{2}\)
When d = \(\frac{1}{2}\)
a + 4d = 3 ⇒ a + 2 = 3 ⇒ a = 1
Section E
(Case Study Based Questions)
(Section E consists of 3 questions. All are compulsory.)
Question 36.
Last night a big strom hit the city of Cuttack. Wind blew with the speed more than 200 km/hr. Many trees got uprooted, pillars broken. Many places in the city got darken as there was no electricity. An electrician was called to repair the faulty wires. He has to repair an electric fault on a pole of height 5 m. He needs to reach a point 1.3 m below the top of the pole to undertake a repair work as shown in figure.

(i) If the ladder is inclined at 60°. Then find the length of the ladder required.
OR
How far the foot of the ladder should be placed from the foot of the pole?
(ii) At what angle should the ladder of height 10 m to be placed if he has to reach the top of the electric pole?
(iii) Upto what length a ladder of height 4√2 m reaches the pole inclined at an angle of 45°?
Solution:
(i) Given, Height of the pole = 5 m
Height to be reached = 5 -1.3 = 3.7 m
Angle of elevation = 60°
In ΔBDC, Height of ladder = BC
sin 60° = \(\frac{B D}{B C}\)
\(\frac{\sqrt{3}}{2}=\frac{3.7}{B C}\)
BC = \(\frac{3.7 \times 2}{\sqrt{3}}=\frac{7.4}{\sqrt{3}}=\frac{7.4}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}\)
= \(\frac{7.4 \sqrt{3}}{3}\) m
OR
Distance between foot of the pole and foot of the ladder is DC.
tan 60° = \(\frac{B D}{D C}\)
√3 = \(\frac{3.7}{\mathrm{DC}}\)
DC = \(\frac{3.7}{\sqrt{3}}\)
= \(\frac{3.7 \times \sqrt{3}}{3}=\) = 1.23√3 m
(ii) Height of pole = 5 m
Height of ladder = 10 m
Angle of inclination = \(\frac{5}{10}\) = \(\frac{1}{2}\)
= sin 30°
(iii) Length of ladder = 4√2 m
Angle of inclination = 45°
Height it can reach is given by,
sin 45° = \(\frac{\text { Height reached }}{\text { Length of ladder }}\)
\(\frac{1}{\sqrt{2}}=\frac{\text { Height reached }}{4 \sqrt{2}}\)
Height that can be reached = \(\frac{4 \sqrt{2}}{\sqrt{2}}\) = 4 m
Question 37.
A ferris wheel (or a big wheel in the United Kingdom) is an amusement ride consisting of a rotating upright wheel with multiple passenger-carrying components (commonly referred to as passenger cars, cabins, tubes, capsules, gondoals, or pods) attached to the rim in such a way that as the wheel turn, they are kept upright, usually by gravity.
After taking a ride in Ferris wheel, Aarti came out from the crowd and was observing her friends who from the crowd and was observing her friends who were enjoying the ride. She was curious about the different angles and measures that the wheel will form. She forms the figure as given below.
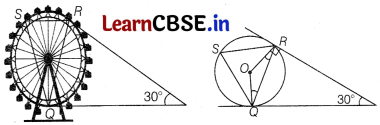
(i) In the given figure, find ∠ROQ. [1]
(ii) Find ∠RSQ. [2]
Or Find ∠ORP [2]
(iii) Find ∠RQP [1]
Solution:
(i) In quadrilateral PQOR, we have
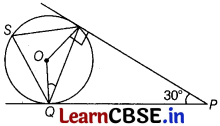
∠QPR + ∠PRO + ∠PQO + ∠ROQ = 360°
⇒ 30° + 90° + 90° + ∠ROQ = 360°
[∵ radius is always perpendicular to the tangent at point of contact]
⇒ ∠ROQ = 360° – 210° = 150°
(ii) We know that angle subtended by an arc at centre is double the angle subtended by it at any other part of the circle.
2 ∠RSQ = ∠ROQ
∠RSQ = \(\frac{1}{2}\) × 150° = 75°
Or
∠ORP = 90° as radius is always perpendicular to the tangent at the point of contact.
(iii) In AQOR, OQ = OR [radii]
Now, ∠ROQ + ∠ORQ + ∠OQR = 180°
⇒ 2∠OQR = 180° – 150°
⇒ 2∠OQR = 30°
⇒ ∠OQR = 15°
Again, ∠OQP = 90° [∵ OQ ⊥ OP]
⇒ ∠OQR + ∠RQP = 90°
⇒ ∠RQP = 90° – 15° = 75°
Question 38.
Due to covid-19 and Lockdown every company is going through many crises. They have to cut-down the salaries of few employees. Before doing so they decided to have the survey of the salaries of company workers. In survey of salaries of workers of a company following data is collected :

Based on the above information answer the following questions:
(i) What will be the upper limit of modal class?
(ii) Estimate the mean salary of the workers.
OR
How many workers have salary more than ₹20,000?
(iii) Class mark of class interval 20 – 25 is equal to:
Solution:
(i) Modal class is the class with maximum frequency i.e. 133.
Hence upper limit of modal class is 15.
(ii)
| Class interval | f i | . x i | . f i x i |
| 5 – 10 | 50 | 7.5 | 375 |
| 10 – 15 | 133 | 12.5 | 1662.5 |
| 15 – 20 | 63 | 17.5 | 1,102.5 |
| 20 – 25 | 16 | 22.5 | 360 |
| 25 – 30 | 8 | 27.5 | 220 |
| Σf i = 270 | Σf i x i = 3720 |
Mean = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)
= \(\frac{3720}{270}\) = 13.778
Mean salary = 13.778 × 1000 = ₹13778
OR
No. of workers have salary more than ₹20,000 = 16 + 8 = 24
(iii) Class mark of a Class interval (20 – 25) = \(\frac{1}{2}\) (lower limit + upper limit)
= \(\frac{1}{2}\)(20 + 25)
= \(\frac{1}{2}\)(45) = 22.5