CBSE Sample Papers for Class 10 Maths Standard Set 2 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Standard with Solutions Set 2 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 2 with Solutions

Time: 3 hrs
Max. Marks:80

Instructions:

1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
(Section-A consists of 20 Questions of 1 mark each)

Question 1.
The sum of three non-zero prime numbers is 100. One of them exceeds the other by 36. Find the largest number. [1]
(a) 73
(b) 91
(c) 67
(d) 57
Answer:
(c) 67

If the sum of three prime numbers is even, then one of the numbers must be 2. [1]
Let the second number be x.
Then, as per the given condition,
x + (x + 36) + 2 = 100
⇒ 2x + 38 = 100 ⇒ x = 31
So, the numbers are 2, 31,67.
Hence, largest number is 67.

Question 2.

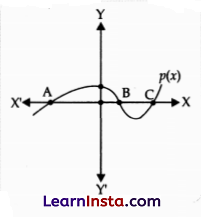
In figure, the graph of a polynomial p(x) is shown. The number of zeroes of
p(x) is
(a) 1
(B) 2
(C) 3
(D) 4
Solution:
(C) 3

Explanation: According to the property of the polynomials,
Number of zeroes = Number of points at which graph intersects the X-axis.

From the figure it is clear that the graph intersects the X-axis at three different points. Therefore, the polynomial has 3 zeroes.

Question 3.
The sum of the first 7 terms of AP sequence, 27, 30, 33, is [1]
(a) 152
(b) 252
(c) 100
(d) 150
Answer:
(b) 252

In the given AP sequence, 27, 30, 33, …….
first term, a = 27 and
common difference, d = 30 – 27 = 3
∵ S _n = \(\frac{n}{2}\) [2a + (n – 1) d]
∴ S ₇ = \(\frac{7}{2}\) [2 × 27 + (7 – 1) × 3]
= \(\frac{7}{2}\) [54 + 18] = \(\frac{7}{2}\) × 72 = 7 × 36 = 252

Question 4.
Two linear equations in variables x and y are given below:
a ₁ x + b ₁ y + c = 0
a ₂ x + b ₂ y +c = 0
Which of the following pieces of information is independently sufficient to determine a solution exists or not for this pair of linear equations?
(i) \(\frac{a_1}{b_1}=\frac{a_2}{b_2}\) = 1
(ii) \(\frac{a_1}{b_1}=\frac{a_2}{b_2}\)
(iii) \(\frac{a_1}{b_1}=\frac{a_2}{b_2}\) ≠ 1
(iv) \(\frac{a_1}{b_1}≠\frac{a_2}{b_2}\)

(A) IV
(B) I and IV
(C) II and IV
(D) I and III
Solution:
(B) I and IV

Explanation: According to given linear equations

Question 5.
If HCF (306,657) = 9, what will be the LCM (306, 657)? [1]
(a) 12338
(b) 22338
(c) 23388
(d) 22388
Answer:
(b) 22338

We know that,
LCM × HCF = Product of two numbers
∴ LCM (306, 657) × HCF (306, 657) = 306 × 657
⇒ LCM × 9 = 306 × 657
⇒ LCM =22338

Question 6.
A(5, 1), B(1, 4) and C(8, 5) are the coordinates of the vertices of a triangle.
Which of the following types of triangle will ΔABC be?
(A) Equilateral triangle
(B) Scalene right-angled triangle
(C) Isosceles right-angled triangle
(D) Isosceles acute-angled triangle
Solution:
(C) Isosceles right-angled triangle

Explanation: In ΔABC

⇒ AB = AC
Thus, ΔABC isisosceles. (i)
By Applying Pythagoras theorem, we can see that,
BC ² = AB ² + CA ²
(5√2) ² = (5) ² + (5) ²
50 = 50
So, ΔABC is right angled triangle
(By converse of Pythagoras theorem) (ii)
From (i) and (ii)
ΔABC is Right Angled Isosceles Triangle.

Question 7.
If a sector of a circle has an area 100 cm³, then the perimeter of this sector is [1]
(a) r + \(\frac{200}{r}\)
(b) 2r + \(\frac{200}{r}\)
(c) r + \(\frac{100}{r}\)
(d) 3r + \(\frac{200}{r}\)
Answer:
(b) 2r + \(\frac{200}{r}\)

We know that the area of a sector of angle θ in a
circle of radius r is \(\frac{\theta}{360^{\circ}} \times \pi r^2\)
\(\frac{\theta}{360^{\circ}} \times \pi r^2\) = 100 ⇒ \(\frac{\theta}{360^{\circ}}=\frac{100}{\pi r^2}\) …….(i)
Now, the perimeter of a sector of angle θ in a circle of radius r is
2r + \(\frac{\theta}{360^{\circ}}\) × 2πr = 2r + \(\frac{100}{\pi r^2}\) × 2πr [using Eq.(i)]
= 2r + \(\frac{200}{r}\)

Question 8.

In the following figure, ST || QR, point S divides PQ in the ratio 4: 5. If ST = 1.6 cm, what is the length of QR?
(Note: The figure is not to scale.)
(A) 0.71 cm
(B) 2 cm
(C) 36 cm
(D) cannot be calculated from the given data.
Solution:
(C) 36 cm

Explanation:

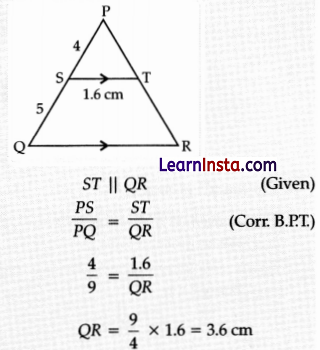
Question 9.
Given that, sin α = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\), then the value of α + β is [1]
(a) 60°
(b) 30°
(c) 0°
(d) 90°
Answer:
(d) 90°

Given, sin α = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\)
⇒ sin α = sin 30° and cos β = cos 60°
[∵ sin 30° = cos 60° = \(\frac{1}{2}\)]
⇒ α = 30° and β = 60°
∴ α + β = 30° + 60° = 90°

Question 10.
A circle has a centre O and radii OQ and OR. Two tangents, PQ and PR, are drawn from an external point, P. In addition to the above information, which of these must also be known to conclude that the quadrilateral PQOR is a square?
(i) OQ and OR are at an angle of 90°.
(ii) The tangents meet at an angle of 90°.
(A) Only (i)
(B) only (ii)
(C) either (i) or (ii)
(D) both (i) and (ii)
Solution:
(C) either (i) or (ii)

Explanation:

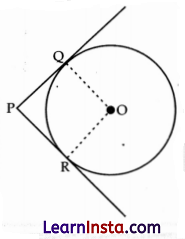
(i) OQ ⊥ PQ
And, OR ⊥ PR
( ∵ Radius is perpendicular to the tangent through the point of contact)
∴ ∠OQP = ∠ORP = 90°
Hence, OQ and OR are at an angle of 90°.
(ii) In square all angles are right angle
∴ ∠QPR = 90°
Thus, tangents meet at an angle of 90°.
Hence, both conditions either (i) or (ii) should be known to conclude that PQOR is a square.

Question 11.
For what value of k, -4 is a zero of the polynomial x² – x -(2k + 2)? [1]
(a) 7
(b) 8
(c) 9
(d) 10
Answer:
(c) 9

Let p(x) = x² – x – (2k + 2)
Since, – 4 is a zero of p(x).
p(-4) = 0
⇒ (- 4)² – (-4) – (2k + 2) = 0
⇒ 16 + 4 – 2k – 2 = 0
⇒ 2k = 18
⇒ k =9

Question 12.
In a right-angled triangle PQR, ∠Q = 90°.
Which of these is ALWAYS 0?
(A) cos P – sec R
(B) tan P – cot R
(C) sin P – cosec R
(D) (cannot be known without knowing the value of P)
Solution:
(B) tan P – cot R

Explanation: In Right Angle Triangle PQR,
∠Q = 90°
(i) cos P – sec R
\(\frac{b}{c}-\frac{c}{a}\) ≠ 0
(ii) tan P – cot R
\(\frac{a}{b}-\frac{a}{b}\) = 0
(iii) sin P – cosec R
\(\frac{a}{c}-\frac{c}{b}\) ≠ 0

Question 13.
If point P lies inside the circle, then the number of tangent(s) drawn from point P, is [1]
(a) 0
(b) 1
(c) 2
(d) None of these
Answer:
(a) 0

If point P lies inside the circle, then no tangent can be drawn.

Question 14.

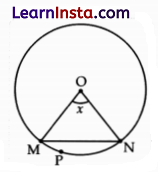
Shown below is a circle with centre O. Chord MN subtends an angle at O.
Which of these is true for the above circle.

(A) only I
(B) only II
(C) both I and II
(D) neither I nor II
Solution:
(C) both I and II

Explanation: According to the formula
(I) Length of Arc = \(\frac{x}{360^{\circ}}\) × 2πr
(II) Area of Minor sector = \(\frac{\pi r^2 \theta}{360^{\circ}}\)

Question 15.
If two solid hemispheres of same base radius r are joined together along their bases, then curved surface area of this new solid is [1]
(a) 4πr²
(b) 6πr²
(c) 3πr²
(d) 8πr²
Answer:
(a) 4πr²

Because curved surface area of a hemisphere is 2πr² and here, we join two solid hemispheres along their bases of radius r, from which we get a solid sphere.
Hence, the curved surface area of new solid
= 2πr² + 2πr² = 4πr²

Question 16.
A number was selected at random from 1 to 100 (inclusive of both number) and it was found to be a multiple of 10.
What is the probability that the selected number is a multiple of 5?
(A) \(\frac{1}{10}\)
(B) \(\frac{1}{5}\)
(C) \(\frac{1}{2}\)
(D) 1
Solution:
(D) 1

Explanation: Total marks = 100
Numbers selected as multiple of 10 = 10
∴ Total outcomes = 10
Favourable outcomes ( Multiples of 5) = 10
P(number is a multiple of 5) = \(\frac{10}{10}\) = 1

Question 17.
In an equilateral ΔABC, G is the centroid. Each side of the triangle is 6 cm. Then, the length of AG is [1]
(a) 2√2 cm
(b) 3√2 cm
(c) 2√3 cm
(d) 3√3 cm
Answer:
(c) 2√3 cm

In an equilateral triangle,
AG : GD = 2 : 1
⇒ AG = 2x and GD = x

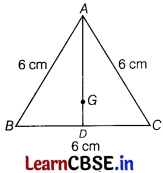
Now, AD = \(\frac{\sqrt{3}}{2}\) a = \(\frac{\sqrt{3}}{2}\) × 6 = 3√3 cm
Again AG + GD = 3√3
2x + x = 3√3
3x = 3√3
x = √3 cm
AG = 2x = 2√3 cm

Question 18.
A survey was conducted on 80 gamers on how many games did they plan in a 6 day. The data is given below.

Number of games	Number of gamers
1-2	20
2-3	24
3-4	10
4-5	12
5-6	8
6-7	4
7-8	2

Which of the following is the modal class?
(A) 1-2
(B) 2-3
(C) 4-5
(D) 7-8
Solution:
(B) 2-3

Explanation: Mode is the number that occurs the highest number of times. So, 24 is Mode.
∴ Modal Class is 2-3.

Directions In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.

Question 19.
Assertion (A): Points A(6,4), B(-4, – 6) and C(4,6) are such that AB = \(\sqrt{200}\), BC = \(\sqrt{208}\) and AC = \(\sqrt{8}\). Since, AB + BC > AC, points A, B, and C form a triangle.
Reason (R): If BC ² = AB ² + AC ² , then ∆ABC is a right-angled triangle, right-angled at A. [1]
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

∴ AB + BC > AC and AB +AC > BC
[∵ sum of the two sides is greater than the third side]
∴ ABC is a triangle.
Also, BC ² = AB ² + AC ²
[∵ \(\sqrt{208}^2\) = \(\sqrt{200}^2\) + \(\sqrt{8}^2\)]
∴ ABC is a right-angled triangle.
So, both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Question 20.
Assertion (A): If the second term of an A.P., is 13 and the fifth term is 25, then its 7 ^th term is 33.
Reason (R): If the common difference of an A.P. is 5, then a ₁₈ – a ₁₃ is 25.
Solution:
(B) Both (A) and (R) are true but (R) is not the correct explanation of the (A).

Explanation: In case of assertion:
In the given A.P., a ₂ = 13 and a ₅ = 25
a + d =13
a + 4d = 25
Solving these equations, we get a = 9 and d = 4
Thus,
a _n = a +(n – 1)d
⇒ a ₇ = 9 + (7 – 1)4 = 33
∴ Assertion is true.
In case of reason:
In the given A.P., d = 5
Thus,
a ₁₈ – a ₁₃ = a + 17d – a – 12d = 5d = 25
∴ Reason is true.
Hence, both assertion and reason are true but reason is not the correct explanation for assertion.

Section B
(Section B consists of 5 questions of 2 marks each)

Question 21.
Check whether the lines x + y = 1 and 2x + y = x + 2 are either parallel or perpendicular. [2]
Solution:
We have, x + y = 1
and 2x + y = x +2 =>x + y = 2
On comparing both equations with ax + by + c = 0,
we get,
a ₁ = 1, b ₁ =1, c ₁ = -1, a ₂ = 1, b ₂ = 1 and c ₂ = -2
Here \(\frac{a_1}{a_2}=\frac{1}{1}\), \(\frac{b_1}{b_2}=\frac{1}{1}\) and \(\frac{c_1}{c_2}=\frac{1}{2}\)
∴ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

Question 22.

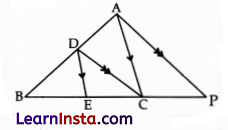
In the adjoining figure, DE || AC and DC || AP. Prove that \(\frac{B E}{E C}\) = \(\frac{B C}{C P}\)
Solution:
In ΔABP,
DC || AP [Given]
\(\frac{B D}{D A}\) = \(\frac{B C}{C P}\)  (From BPT) … (i)
In ΔABC,
DE || AC [Given]
\(\frac{B D}{D A}\) = \(\frac{B E}{E C}\)  (From BPT) … (ii)
From equations (i) and (ii), we have
\(\frac{B E}{E C}\) = \(\frac{B C}{C P}\) Hence Proved.

Question 23.
The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 min. [2]
Solution:
Given, length of minute hand = radius of the circle
⇒ r = 14 cm
∵ Angle swept by the minute hand in 60 min = 360°
∴ Angle swept by the minute hand in 5 min
= \(\frac{360°}{60°}\) × 5 = 30°
Now, area of the sector with, r = 14 cm and θ = 30°
= \(\frac{\theta}{360^{\circ}}\) × πr² = \(\frac{360°}{60°}\) × \(\frac{22}{7}\) × 14 × 14
= \(\frac{11 \times 14}{3}\) = \(\frac{154}{3}\) cm²
Thus, the required area swept by the minute hand by
5 min = \(\frac{154}{3}\) cm².

Question 24.
(A) If cos (A + 2B) = 0, 0° ≤ (A + 2B) ≤ 90° and cos (B – A) = \(\frac{\sqrt{3}}{2}\), 0° ≤ (B – A) ≤ 90° then find cosec (2A + B).
Show your work.
Solution:
cos (A + 2B) = 0 (given)
⇒ cos (A + 2B) = cos 90° ( ∵ cos 90° = 0)
A + 2B = 90° … (i)
Now, cos (B – A) = \(\frac{\sqrt{3}}{2}\)
⇒ cos (B – A) = cos 30°
B – A = 30° … (ii)
Add both the equations
A + 2B + B – A = 90° + 30°
⇒ 3B = 120°
⇒ B = 40°
Substitute value of B in equation (i)
A + 2 × 40° = 90°
A = 10°
Thus, cosec (2A + B) = cosec (2 × 10° + 40°)
= cosec 60°
= \(\frac{2}{\sqrt{3}}\)
Hence, cosec (2A + B) = \(\frac{2}{\sqrt{3}}\)

OR

State whether the following statements are true or false. Give reasons
(i) As the value of sin θ increases, the value of tan θ decreases.
(ii) When the value of sin θ is maximum, the value of cosec θ is also maximum.
(Note: 0° < θ < 90°)
Solution:
(i) False
We know that, tan θ = \(\frac{sin θ}{cos θ}\)
So, tan θ is directly proportional to sin θ.
Hence, if sin θ increases the value of tan θ also increases.

(ii) False
As sin θ = \(\frac{1}{cosec θ}\)
So, sin θ is inversely proportional to cosec θ.
Hence if sin θ is maximum the value of cosec θ is not maximum.

Question 25.
In the given figure, line BD || CE. If AB = 1.5 cm, BC = 6 cm and AD =2 cm. Find DE. [2]

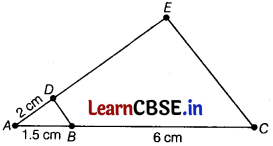
Solution:
In ∆ADB and ∆AEC,
∠ADB = ∠AEC
[corresponding angles as BD || CE]
∠ABD = ∠ACE
[corresponding angles as BD || CE]
∠A = ∠A [common]
∴ ∆ADB ~ ∆AEC
[by AAA similarity criterion]
⇒ \(\frac{A D}{A E}=\frac{A B}{A C}\)
∴ \(\frac{2}{2+DE}=\frac{1.5}{1.5+6}\) ⇒ \(\frac{2}{2+DE}=\frac{1.5}{7.5}\)
⇒ \(\frac{2}{2+DE}=\frac{1}{5}\) ⇒ 2 + DE = 10
⇒ DE = 8cm

Section C
(Section C consists of 6 questions of 3 marks each)

Question 26.
Find the smallest pair of 4-digit numbers such that the difference between them is 303 and their HCF is 101.
Show your steps.
Solution:
Let a and b be the required numbers.
Let the smallest 4 digit be 1000
HCF of two number =101 (given)
On dividing 1000 by 101
We get, remainder = 91
Now Subtract it from 101 = 101 – 91 = 10
∴ First number (a) = 1000 + 10 = 1010
It is given that, b – a = 303
By subsituting value of ‘b’ in above equation we get,
b – 1010 = 303
b = 303 + 1010
= 1313
Thus, pair of smallest 4 digit numbers are 1010, 1313.

Question 27.
Prove that
\(\frac{1}{2}\) = 1 + sec θ cosec θ.
Or
If sec θ = x + \(\frac{1}{4x}\), then prove that
sec θ + tan θ = 2 x or \(\frac{1}{2x}\). [3]
Solution:

Or
We have sec θ = x + \(\frac{1}{4x}\) ……(i)
∵ tan² θ = sec² θ – 1

Question 28.
(A) 3(3) ^2m + 11(3) ^m = 4
Use the substitution (3) ^m = x to solve for m. Show your steps.
Solution:
Given
3(3) ^2m + 11(3) ^m = 4
⇒ 3 × (3 ^m ) ² + 11(3) ^m = 4
By substituting value of 3 ^m we get
3x ² + 11x – 4 = 0
3x ² + 12x – x – 4 = 0
3x(x + 4) – 1 (x + 4) = 0
(3x – 1)(x + 4) = 0
x = \(\frac{1}{3}\) and x = -4
3 ^m = \(\frac{1}{3}\)
3 ^m = 3 ^-1
Hence, m = -1
But 3 ^m = -4 is not possible as 3 to any variable power cannot be negative.

OR

(B) Find all the possible value(s) of x for the following equation to be true.
\( \sqrt{(15-2 x)}\) = x
Show your steps and give valid reasons.
Solution:
\( \sqrt{(15-2 x)}\) = x
On squaring both sides we get
(\( \sqrt{(15-2 x)}\)) ² = x ²
15 – 2x – x ² = 0
-x ² – 2x + 15 = 0
x ² + 2x – 15 = 0
x(x + 5) – 3 (x + 5) = 0
(x + 5) (x – 3) =0
So, x = -5 and x = 3
Now, if x = -5
(\( \sqrt{(15-2×(-5))}\) – (-5) = 0
\( \sqrt{(15+10)}\) + 5 = 0
√25 + 5 = 0
5 + 5 = 0
10 ≠ 0
LHS ≠ RHS
∴ x ≠ -5
If x = 3
\( \sqrt{(15-2×3)}\) – 3  =0
\( \sqrt{(15-6)}\) – 3 =0
√9 – 3 = 0
3 – 3 = 0
0 = 0
LHS = RHS
∴ x = 3

Question 29.
In an AP, if the pth term is q and the qth term is p, then show that the nth term is (p + q – n). [3]
Solution:
Let a be the first term and d be the common difference of the given AP Then,
T _p = a + (p – 1)d and T _q = a + (q – 1)d
Now, T _p = q and T _q = p [given]
∴ a + (p – 1)d = q …(i)
and a + (q – 1)d = p ……(ii)
On subtracting Eq. (i) from Eq. (ii), we get
(q – p)d = (p – q) =* d = -1
On putting d = -1 in Eq. (i), we get a = (p + q – 1)
Thus, a = (p + q – 1) and d = -1
∴ nth term = a + (n – 1)d = (p + q – 1) + (n – 1) × (-1)
= p + q – n
Hence, the nth term = (p + q – n).

Question 30.
Prove that \(\frac{\cos ^4 x-\sin ^4 x}{1-\tan x}=\frac{(\cot x+1)}{\sec x {cosec} x}\)
Solution:

Question 31.
In the given figure, PT and PS are tangents to a circle from a point P such that PT = 4 cm and ∠TPS = 60°.

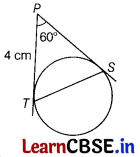
Find the length of chord TS. How many lines of same length TS can be drawn in the circle?
Or
AB is a diameter and AC is a chord of a circle such that ∠BAC = 30°. If the tangent at C intersects AB produced at D, then prove that BC – BD. [3]
Solution:
We know that tangents drawn from external point to the circle are equal in length.
Here, P is an external point.
∴ PS = PT = 4cm
So, ∠PTS = ∠PST
[∵ angles opposite to equal sides are equal]
In APTS, we have
∠PTS + ∠PST + ∠TPS = 180°
[by angle sum property of triangle]
⇒ ∠PTS + ∠PTS + 60° = 180°
[∵ ∠PST = ∠PTS and ∠TPS = 60° ]
⇒ 2∠PTS =180° – 60°
⇒ 2∠PTS = 120°
⇒ ∠PTS = \(\frac{120°}{2}\) = 60°
∴ ∆PTS is an equilateral triangle.
Hence, TS = 4 cm
Here, infinite lines of same length TS can be drawn in a circle.

Or

Given AB is the diameter of the circle with centre O and Dt is the tangent of the circle and ∠BAC = 30°.
To prove: BC = BD
Construction Join O to C.

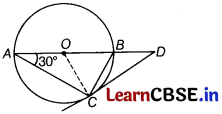
Proof Since, OC ⊥ CD
[∵ the tangent at any point of a circle is perpendicular to the radius through the point of contact]
∴∠OCB + ∠BCD = 90°
Now, OC = OA [radii]
⇒ ∠OCA = ∠OAC
[angles opposite to equal sides are equal]
∴∠OCA = 30°
Now, ∠ACB = 90° [angle in a semi-circle]
∴ ∠OCA + ∠OCB = 90°
⇒ ∠OCB = 60° and ∠BCD = 30°
In ∆ACD, ∠ACD + ∠CAD + ∠ADC = 180°
⇒ 120° + 30° + ∠ADC = 180°
⇒ ∠ADC = 30°
∴ In ∆BCD,
∠BCD = ∠BDC = 30°
∴ BC = BD Hence proved.

Section D
(Section D consists of 4 questions of 5 marks each)

Question 32.
(A) Two water taps together can fill a tank in 1\(\frac{7}{8}\) hours. The tap with longer diameter takes 2 hours less than the tap with smaller one to fill the tank separately. Find the time in which each tap can fill the tank separately.
Solution:
Let the time taken by the smaller diameter tap = xh
∴ lime for larger diameter tap = (x – 2) h

15(2x – 2) = 8x(x – 2)
30x – 30 = 8x ² – 16x
8x ² – 46x + 30 = 0
4x ² – 23x + 15 = 0
4x ² – 20x – 3x + 15 = 0
4x(x – 5) – 3(x – 5) = 0
(4x – 3)(x – 5) = 0
x = \(\frac{3}{4}\) or x = 5
If x = \(\frac{3}{4}\),
then x – 2 = \(\frac{3}{4}\) – 2
x = \(\frac{-5}{4}\).
Since, time cannot be negative, we neglect x = \(\frac{-5}{4}\).
Therefore, x = 5 and x – 2 = 5 – 2 = 3
Hence, time taken by larger diameter tap = 3 hours and time taken by smaller diameter tap = 5 hours.

OR

(B) To fill a swimming pool two pipes are used. If the pipe of larger diameter used for 4 hours and the pipe of smaller diameter for 9 hours, only half of the pool can be filled. Find, how long it would take for each pipe to fill the pool separately, if the pipe of smaller diameter takes 10 hours more than the pipe of larger diameter to fill the pool?
Solution:
Let the time taken by larger pipe alone to fill the tank = x hours
Therefore, the time taken by the smaller pipe = x + 10 hours
Water filled by larger pipe running for 4 hours = \(\frac{4}{x}\) litres
Water filled by smaller pipe running for 9 hours = \(\frac{9}{x+10}\) litres
According to questions, \(\frac{4}{x}\) + \(\frac{9}{x+10}\) = \(\frac{1}{2}\)
Which on simplification gives:
x ² – 16x – 80 = 0
x ² – 20x + 4x – 80 = 0
x(x – 20) + 4 (x – 20) = 0
(x + 4)(x- 20) = 0
x = -4, 20
x cannot be negative.
Thus, x =20
x + 10 = 30
Larger pipe would alone fill the tank in 20 hours and smaller pipe would fill the tank alone in 30 hours.

Question 33.
The angle of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m. [5]
Solution:
Let the tower be represented by AB in the figure.
Let AB = h m.

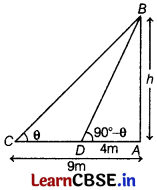
∴ In right angled ∆ABC,
we have
\(\frac{A B}{A C}\) = tan θ
⇒ \(\frac{h}{9}\) = tan θ ……..(i)
In right angled ∆ABD,
we have
\(\frac{A B}{A D}\) = tan(90°- θ) = cot θ
⇒ \(\frac{h}{4}\) = cot θ ……..(i)
On multiplying Eqs. (i) and (ii), we get
\(\frac{h}{9}\) × \(\frac{h}{4}\) = tan θ × cot θ = 1 [∵ tan x × cot x = 1]
⇒ \(\frac{h^2}{36}\) = 1
⇒ h² = 36
⇒ h = ± 6m
∴ h = 6m [∵ height is positive only]
Thus, the height of the tower is 6 m.

Question 34.
(A) A bird feeder tube has a diameter of 8 cm and height of 28 cm. The tube has 7 circular openings of 2 cm diameter each for the birds to eat from. The tube can hold a maximum of 3 kg of bird food.
(Note: The image is for visual representation only.)
If the birds eat an average of 75 g of food per hour, what will be the height of the food in the tube after 5 hours? Show your work.
(Note: Take π as \(\frac{22}{7}\))
Solution:
Volume of feeder tube = πr ² h
= \(\frac{22}{7}\) × 4 × 4 × 28
= 1408 cm ³
Birds can eat 75 g in an hour.
So, Bird’s can eat in 5 hours = 75 × 5 = 375 g
Total capacity of tube = 3 kg
= 3000 g
So, Volume of feeder tube = capacity of tube
1408 cm ³ = 3000 g
375 g = 176 cm ³
Volume of tube after 5 hours = 1408 – 176
= 1232 cm ³
i.e., πr ² h = 1232
h = \(\frac{(1232 \times 7)}{(22 \times 4 \times 4)}\) = 24.5
Thus, height of food in tube after 5 hours = 24.5 cm

OR

(B) Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/hour. How much area will it irrigate in 30 minutes; if 8 cm standing water is needed?

Solution:
Canal is of the shape of cuboid, where
Breadth = 6 m
Depth = 1.5 m
and Speed of water = 10 km/h
Length of water moved in 60 minutes = 10 km
Length of water moved in 1 minute = \(\frac{1}{60}\) × 10 km
Length of water moved in 30 minutes
= \(\frac{30}{60}\) × 10 = 5 km = 5000 m
Now, volume of water in canal = Length × Breadth × Depth
= 5000 × 6 × 1.5 m ³
Now, volume of water in canal = volume of water in area irrigated
5000 × 6 × 1.5 m ³ = Area irrigated × 8 cm
5000 × 6 × 1.5 m ³ = Area irrigated × \(\frac{8}{100}\) m
∴ Area irrigated = \(\frac{5000 \times 6 \times 1.5 \times 100}{8}\)m ³
= 5.625 × 10 ⁵ m ²

Question 35.
A right angled triangle whose sides other than hypotenuse are 15 cm and 20 cm, is made to revolve about its hypotenuse. Find the volume and surface area of the double cone, so formed. [take, π =3.14]
Or
A solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is 4 cm and the diameter of the base is 8 cm. If a right circular cylinder circumscribes the solid. Find how much more space it will cover? [5]
Solution:
Let BAC be a right angled triangle such that
AB = 15 cm and AC = 20 cm.
Using Pythagoras theorem, we have

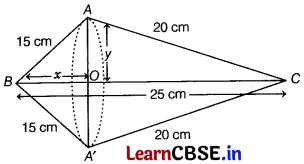
(BC) ² = (AB) ² + (AC) ²
⇒ (BC) ² = 15 ² + 20 ²
⇒ (BC) ² = 225 + 400 = 625
∴ SC = 25 cm
[taking positive square root]

Let OB = x and OA = y.
Again, using Pythagoras theorem in AOAB and AOAC, we have
AB ² = OB ² + OA ²
⇒ 15 ² = x ² + y ²
⇒ x ² + y ² = 225 …(i)
and AC ² = OA ² + OC ²
⇒ 20 ² = y ² + (25 – x)
⇒ (25- x) ² + y ² = 400 …(ii)
On subtracting Eq. (i) from Eq. (ii), we get
⇒ {(25 – x) ² + y ² } – {x ² + y ² } = 400 – 225
⇒ (25 – x) ² – x ² = 175
⇒ (25 – x – x)(25 – x + x) = 175
[∵ a ² – b ² = (a – b) (a + b)]
⇒ (25 – 2x) × 25 = 175
⇒ 25 – 2x = 7
⇒ 2x = 18
On putting x = 9 in Eq. (i), we get
81 + y ² = 225
⇒ y ² = 144
∴ y = 12
[taking positive square root]
Thus, we have OA = 12 cm and OB = 9 cm

∴ Volume of the double cone
= Volume of cone CAA’ + Volume of cone BAA’
= \(\frac{1}{3}\) π (OA) ² × OC + \(\frac{1}{3}\) π (OA) ² × OB
= \(\frac{1}{3}\) π × 12 ² × 16 + \(\frac{1}{3}\) π × 12 ² × 9
= \(\frac{1}{3}\) π × 144(16 + 9)
= \(\frac{1}{3}\) × 3.14 × 144 × 25
= 3768 cm³
∴Total surface area of the double cone
= Curved surface area of cone CAA’ + Curved surface area of cone BAA’
= π × OA × AC + π × OA × AB
= π × 12 × 20 + π × 12 × 15= 420 π
= 420 × 3.14= 1318.8 cm²

Or

Let 6PC be the hemisphere and ABC be the cone mounted on the base of the hemisphere.
Let EFGH be the right circular cylinder circumscribing the given toy.

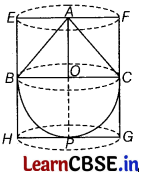
We have, height of cone, OA = 4 cm
Diameter of the base of the cone, d =8 cm
∴ Radius of the base of cone, r = \(\frac{d}{2}\) = \(\frac{8}{2}\) = 4 cm
Here, AP = AO + OP = 4 + 4 = 8 cm
∴ Required space
= Volume of cylinder – (Volume of cone + Volume of hemisphere)

Hence, the right circular cylinder covers 64π cm³ more space than the solid toy.

Section E
(Case study based questions are compulsory)

Question 36.
Answer the questions based on the given information.
Shown below is a house of cards, a structure created by stacking playing cards on top of each other in the shape of a pyramid. Each small triangle is made using 3 cards and each layer has 1 less triangle than the layer below it.

Ankit and his friends were having a sleepover and wanted to do something fun. One of the friends suggested that they could make a house of cards.

(i) Ankit and his friends want to use 3 cards in the top layer and 18 in the bottom layer. From an AP showing the number of cards in each layer starting from the layer.
Solution:
Let number of cards in top layer be (a) = 3
Common-Difference (d) = 3
∴ AP = 3, 6, 9, 12, 15, 18.

(ii) They have a total of 360 cards with them.
Find the maximum number of layers that Ankit and his friends can make using the cards they have if they want to have 1 triangle (3 cards) at the top layer. Show your work.
Solution:
Sum of all cards (S _n ) = 360
Total number of layers = n
a = 3; d = 3
(S _n ) = \(\frac{n}{2}\) [2a + (n – 1)d]
360 = \(\frac{n}{2}\) [6 + (n – 1)3]
720 = 6n + 3n2 -3n
3n2 + 3n – 720 = 0
n2 + n – 240 = 0
n2 + 16n – 15n – 240 = 0
n(n + 16) – 15 (n + 16) =0
(n + 16)(n – 15) =0
n = -16 and 15
Thus maximum number of layers = 15

OR

Ankit is planning to make a pyramid with the top and bottom 10 layer containing 15 and 138 cards respectively.
How many layers will such a pyramid have? Show your work.
Solution:
(a) = 15
(d) = 3
T _n = a + (n – 1)d
138 = 15 + (n – 1)3
123 = 3n – 3
\(\frac{126}{3}\) = n
n = 42
Thus number of layers = 42

(iii) Which mathematical concept is used here?
Solution:
This question is based on mathematical concept Arithmetic Progression.

Question 37.
No Smoking Campaign
All of them know that smoking is injurious for health. So, college students decide to make a campaign.

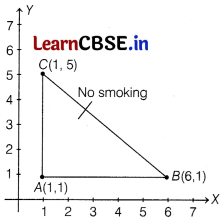
To raise social awareness about the hazards of smoking, a school decided to start a “No SMOKING” campaign.
10 students are asked to prepare campaign banners in the shape of triangle (as show in the figure)
Based on the above information, answer the following questions.
(i) If cost of per cm² of banner is ₹ 2, then find the overall cost incurred on such campaign. [2]
Or
If we want to draw a circumscribed circle of given, then find the coordinates of the centre of circle. [2]
(ii) If we draw the image of figure about the line BC, then find the total area. [1]
(iii) Find the centroid of the given triangle. [1]
Solution:
(i) Here, from the figure,
coordinates of A = (1, 1),
coordinates of B = (6, 1)
and coordinates of C = (1, 5)
∴ Area of banner = Area of ∆ABC
Now, area of one banner = \(\frac{1}{2}\) × AB × AC
= \(\frac{1}{2}\) × 5 × 4
= 10 sq units
Then, area of 10 banners
= 10 × Area of one banner
∴ Cost of 10 banners at the rate of ₹ 2 per cm²
= 2 × Area of 10 banners
= 2 × 10 × 10
= ₹ 200

Or

The centre of the circumscribed circle of a given triangle is the mid-point of the hypotenuse.
Centre of circle = Mid-point of BC
= \(\left(\frac{1+6}{2}, \frac{5+1}{2}\right)\)
= \(\left(\frac{7}{2}, \frac{6}{2}\right)\)
= (3.5, 3)

(ii) Total area of the required figure
= 2 × Area of ∆ABC
= 2 × 10 = 20 sq units

(iii) Centroid of the triangle (x, y)
= \(\left(\frac{1+1+6}{3}, \frac{5+1+1}{3}\right)\)
= \(\left(\frac{8}{3}, \frac{7}{2}\right)\)
= (2.6, 2.3)

Question 38.
In the giant wheel shown below, Gagan is sitting in one of the cabins which is 12 m high from the platform. Jyoti and Karan are sitting in the lowest and the highest cabins from the platform respectively. From Gagan, the angle of depression of Jyoti and the angle of elevation of Karan is 30° and 60° respectively.
(Note: The figure is not to scale.)

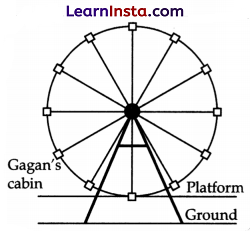
Solution:
Given: Distance of Gagan from platform = 12 m
Angle of elevation of Kiran = 60°
Angle of depression of Jyoti = 30°

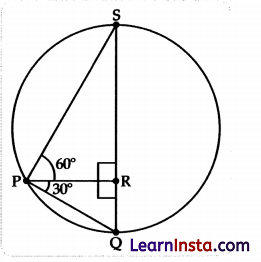
(Note: The figure is not to scale.)
In given figure:
Position of Gagan = Point P
Position of Karan = Point S
Position of Jyoti = Point Q

(i) What will be the angle of elevation of Gagan from Jyoti?
Solution:
Angle of elevation = Angle of depression
∴ Angle of elevation of Gagan from Jyoti = 30°

(ii) Find the diameter of the giant wheel?
Solution:
In ΔPRQ
∠R = 90°
RQ = 12 cm
(As Gagan is 12 m high from platform)

SR = 12 × 3 = 36 m
Thus, Diameter of the giant wheel = SR + RQ
= 36 + 12
= 48 m

OR

Find the distance between Gagan and Karan.
Solution:
In ΔPSR
∠PRS = 90°

(iii) What will be the angle of depression of Gagan from Karan?
Solution:
Angle of depression of Gagan from Karan = 60°