CBSE Sample Papers for Class 10 Maths Standard Set 11 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths with Solutions Set 11 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 11 with Solutions

Time: 3 hrs
Max. Marks: 80

Instructions

1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
(Section A consists of 20 questions of 1 mark each.)

Question 1.
Which of the following is not an irrational number? [1]
(a) 7\(\sqrt{5}\)
(b) \(\sqrt{2}\) + 2\(\sqrt{2}\)
(c)(\(\sqrt{7}\)– 3)- \(\sqrt{7}\)
(d) \(\sqrt{3}\) + 2
Answer:
(c)(\(\sqrt{7}\)– 3)- \(\sqrt{7}\)

We have, (\(\sqrt{7}\) – 3) – \(\sqrt{7}\) = \(\sqrt{7}\) – 3 – \(\sqrt{7}\) = -3
Since – 3 is a rational number.
So, (\(\sqrt{7}\) – 3) – \(\sqrt{7}\) is a rational number.

Question 2.
What is the product or sum of a rational and irrational numbers?
(a) Rational number
(b) Natural number
(c) Irrational number
(d) Integer number
Answer:
(c) Irrational number
Explanation: Product or sum of rational and irrational number will always be a irrational number.
e.g., 2 + √3 is irrational number
5 √7 is also a irrational number.

Question 3.
If the HCF of 408 and 1032 is expressed in the form 1032 × 2 + 408 × p, then the value of p is [1]
(a) 5
(b) -5
(c) 4
(d) -4
Answer:
(b) -5

Prime factors of given numbers are
408 = 2 ³ × 3 × 17
and 1032 = 2 ³ × 3 × 43
HCF (408, 1032) = 2 ³ × 3 ¹ = 24
But HCF expressed in the form
1032 × 2 + 408 × p = 24
⇒ 2064 + 408 × p = 24
⇒ 408p = – 2040
⇒ p = –\(\frac{2040}{408}\) = -5

Question 4.
What is a quadratic polynomial whose sum of zeroes is 3 and product of zeroes is – 2?
(a) x ² + 3x – 2
(b) x ² – 3x – 2
(c) x ² + 3x + 2
(d) x ² – 3x + 2
Answer:
(b) x ² – 3x – 2
Explanation: Given, sum of zeroes, S = 3
Product of zeroes, P = – 2
Required polynomial is given by
f(x) = x ² – (Sum of zeroes)x + Product of zeroes
⇒ f(x) = x ² – 3x – 2

Question 5.
The discriminant of the quadratic equation 6x ² – 7x + 2 = 0 is [1]
(a) 0
(b)-1
(c) 1
(d) 2
Answer:
(c) 1

Given, 6x ² – 7x + 2 = 0 …….. (i)
On comparing Eq. (i) with ax ² + bx + c = 0, we get
a = 6, b = -7 and c = 2
We know that, D = b ² – 4ac
= (-7) ² – 4(6)(2)
= 49 – 48 = 1
Hence, the value of the discriminant is 1.

Question 6.
For what value of k, the system equation 2x + 3y =5 and 4x + ky = 10 has infinite solutions?
(a) 7
(b) 8
(c) 6
(d) 4
Answer:
(c) 6
Explanation: Given system of equation is
2x + 3y – 5 = 0
4x + ky – 10 = 0
Here, a ₁ = 2, b ₁ = 3, c ₁ = -5
a ₂ = 4, b ₂ = k, c ₂ = -10
For infinite solutions, \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)
⇒ \(\frac{2}{4}=\frac{3}{k}=\frac{5}{10}\)
⇒ \(\frac{2}{4}=\frac{3}{k}\)
2k = 3 × 4
k = 6
Hence, for k = 6 given system of equations has infinitely many solutions.

Question 7.
In the given figure, ∠ABC = 90° and BD ⊥ AC. If BD = 8 cm and AD = 4 cm, then the value of CD is [1]

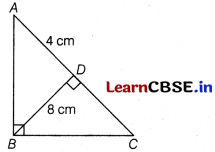
(a) 16 cm
(b) 8 cm
(c) 4 cm
(d) 10 cm
Answer:
(a) 16 cm

Given, BD = 8 cm and AD = 4 cm
In ∆ADB and ∆BDC,
∠BDA = ∠CDB [each 90°]
∠DBA = ∠DCB [each (90°-∠A)]
∆ADB~∆BDC [by AA similarity criterion]
⇒ \(\frac{B D}{C D}\) = \(\frac{A D}{B D}\)
⇒ CD = \(\frac{(B D)^2}{A D}\) = \(\frac{8^2}{4}\) = \(\frac{64}{4}\) = 16 cm

Question 8.
What is the probability that a non-leap year selected at random will contain 53 Sundays?
(a) \(\frac{1}{7}\)
(b) 7
(c) \(\frac{1}{6}\)
(d) \(\frac{6}{7}\)
Answer:
(a) \(\frac{1}{7}\)
Explanation: A non-leap year has 365 days and so it has 52 weeks and 1 day.
This 1 day can be Sunday or Monday or Tuesday or Wednesday or Thursday or Fridays or Saturday. Thus, total outcomes = 7
Favourable outcome = 1
Probability = \(\frac{\text { Number of favourable outcomes }}{\text { Number of total outcomes }}\) = \(\frac{1}{7}\)
Number of total outcomes 7

Question 9.
If cosec A = 2, then the value of \(\frac{1}{\tan A}\) + \(\frac{\sin A}{1+\cos A}\) is [1]
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(c) 2

Given, cosec A = 2 ⇒ A = 30°

Question 10.
If P(E) = 0.05, what is the probability of ‘not E’?
(a) 0.93
(b) 0.95
(c) 0.89
(d) 0.98
Answer:
(b) 0.95
Explanation: Given: P(E) = 0.05
P(not E) = 1 – 0.05 = 0.95
The probability of ‘not E’ is 0.95.

Question 11.
The number of solutions of the pair of equations x = 0 and x = 3 is [1]
(a) infinite many solutions
(b) no solution
(c) one solution
(d) None of the above
Answer:
(b) no solution

x = 0 is the Y-axis and x = 3 is the line parallel to the Y-axis at a distance of 3 units from it. These lines do not meet anywhere. So, no solution exists.

Question 12.
Find the ratio in which the line segment joining A(1, -5) and B(-4, 5) is divided by the X-axis?
(a) 1 : 1
(b) 2 : 1
(c) 1 : 2
(d) 2 : 5
Answer:
(a) 1 : 1
Explanation: Given Let K : 1 be the ratio in which X-axis divides the line joining A (1, -5) and B (-4, 5).
Let P be the point on X-axis that divides the line AB, and then
P(x, y) = (\(\frac{-4 \mathrm{~K}+1}{\mathrm{~K}+1}, \frac{5 \mathrm{~K}-5}{\mathrm{~K}+1}\))
As P(x, y) lies on X-axis P(x, 0) = (\(\frac{-4 \mathrm{~K}+1}{\mathrm{~K}+1}, \frac{5 \mathrm{~K}-5}{\mathrm{~K}+1}\))
⇒ \(\frac{5 \mathrm{~K}-5}{\mathrm{~K}+1}\) = 0
5 = 5K
K = 1
∴ Point (x, 0) on X-axis divides the line segment in 1 : 1 ratio.

Question 13.
If a cylinder is filled with water and a spherical ball of radius r is dropped into the cylinder, then the quantity of water spread out, is [1]
(a) 2 × volume of sphere
(b) volume of sphere
(c) 3 × volume of sphere
(d) None of the above
Answer:
(b) volume of sphere

When we draped the ball into a cylinder full of water, the quantity of spreading water is equal to the volume of the sphere i.e. \(\frac{4 \pi}{3}\)r ³

Question 14.
Find the 17th term of A.P. 19,14, 9, …………..
(a) 61
(b) 16
(c) -61
(d) 60
Answer:
(c) – 61
Explanation: Given A.P. is 19, 14, 9, …………..
Here First term, a = 19
Common difference, d = 14 -19 = – 5
We know that n ^th term of an A.P. is given as,
a _n = a + (n – 1 )d
∴ a ₁₇ = a + (17 – 1 )d
= a + 16 d
= 19 + 16(- 5) = 19 – 80
⇒ a ₁₇ = -61.

Question 15.
The simplified value of(l -cos ² A) cosec ² A is [1]
(a) -1
(b) 1
(c) 0
(d) 2
Answer:
(b) 1

We have, (1 – cos ² A) cosec ² A
= cosec ² A – cos ² A cosec ² A
= cosec ² A – cos ² A∙\(\frac{1}{\sin ^2 A}\)
= cosec ² A – cot ² A = 1

Question 16.
Find the HCF of 81 and 237.
(a) 3
(b) 2
(c) 79
(d) 9
Answer:
(a) 3
Explanation: Given integers are 81 and 237
Prime factors of 81 =3 × 3 × 3 × 3
Prime factors of 237 = 3 × 79
Hence, HCF (81, 237) = 3.

Question 17.
If the points A(4,3) and B(x, 5) are on the circle with centre O (2, 3), then the value of x is [1]
(a) 5
(b) 6
(c) 2
(d) 4
Answer:
(c) 2

Since A and B lie on the circle having centre O. Then, the distance between points A and B from the centre are same as they are radius of the circle.

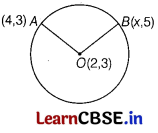
i.e. OA = OB
From the distance formula,
\(\sqrt{(4-2)^2+(3-3)^2}\) = \(\sqrt{(x-2)^2+(5-3)^2}\)
⇒ \(\sqrt{4+0}\) = \(\sqrt{(x-2)^2+4}\)
On squaring both sides, we get
4 = (x – 2) ² + 4
⇒ (x – 2 ) ² = 0 ⇒ x – 2 = 0 ⇒ x = 2

Question 18.
Two circles touch each other externally at P. AB is a common tangent to the circles, touching them
at A and B. The value of ∠APB is:
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Answer:
(d) 90°
Explanation: Let PO meet AB at O such that PO is a tangent.

Thus, AO = PO = OB and ∠AOP = ∠BOP = 90°.
As ΔAOP and ΔBOP are right-angled isosceles triangles.
So, ∠OAP = ∠OPA = ∠OBP = ∠OPB = 45°
Thus, ∠APB = ∠APO + ∠OPB
= 45° + 45° = 90°

Directions In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) If α and β are the zeroes of the polynomial x ² + 2x – 15, then \(\frac{1}{\alpha}\) + \(\frac{1}{\beta}\) is \(\frac{2}{15}\).
Reason (R) If α and β are the zeroes of a quadratic polynomial ax ² + bx + c, then
α + β = –\(\frac{b}{a}\) and αβ = \(\frac{c}{a}\). [1]
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Let f(x) = x ² + 2x – 15
On comparing f(x) with ax ² + bx + c = 0, we get a = 1, b = 2 and c = -15
Then, α + β = -2 and α∙β = -15
⇒ \(\frac{1}{\alpha}\) + \(\frac{1}{\beta}\) = \(\frac{\alpha+\beta}{\alpha \cdot \beta}\) = \(\frac{-2}{-15}\) = \(\frac{2}{15}\)
So, both Assertion (A) and Reason (R) are true and Reason (R) is a correct explanation of Assertion (A).

Question 20.
Statement A (Assertion): If two tangent segments are drawn to one circle from the same external point, then they are congruent.
Statement R (Reason): If a line touches a circle, then the perpendicular distance of the line from the center of the circle is equal to the radius 20 of the circle.
Solution:
(b) Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Explanation: As per the two-tangent theorem, if two tangent segments are drawn to one circle from the same external point, then they are congruent. So, the assertion is proved to be correct, For the reason, as per the tangent to a circle theorem “A line is tangent to a circle if and only if the line is perpendicular to the radius drawn to the point of tangency/7 So, the statement in the reason is also true. But they don’t support or define each other.

Section B
(Section B consists of 5 questions of 2 marks each.)

Question 21.
Solve the following system of equations by elimination method [2]
x + y = a – b
ax – by = a ² + b ²
Answer:
The given equations are
x + y = a – b ………..(i)
ax – by = a ² + b ² ……….(ii)
On multiplying Eq. (i) by b, we get
bx + by = ab – b ² ……….(iii)
On adding Eqs. (ii) and (iii), we get
(ax – by) + (bx + by) = (a ² + b ² ) + (ab – b ² )
(a + b)x = a ² + ab = a(a + b)
⇒ x = \(\frac{a(a+b)}{a+b}\) = a
On putting x = a in Eq . (i), we get
a + y = a – b ⇒ y = a – b – a = -b

Or

In a two-digit number, the ten’s digit is three times the unit’s digit. When the number is decreased by 54, then the digits are reversed. Find the number. [2]
Answer:
Let the digit in unit’s place be x and the digit in ten’s place be y.
Then, number = 10y + x
According to the given condition,
y = 3x ……. (i)
Number obtained by reversing the digits = 10x + y
If the number is decreased by 54, the digits are reversed.
∴ Number – 54 = Number of obtained by reversing the digits
⇒ 10y + x – 54 = 10x + y
⇒ 9x – 9y = -54
⇒ x – y = -6
[dividing on both side by 9] ……… (ii)
On putting y = 3x from Eq. (i) to Eq. (ii), we get
x – 3x = -6
⇒ x = 3
On putting x = 3 in Eq. (i), we get
y = 9
Hence, number = 10y + x
= 10 × 9 + 3
= 93

Question 22.
Solve the quadratic equation x ² + 2√2x – 6 = 0.
OR
Solve the quadratic equation 2x ² + ax – a ² = 0 for x.
Solution:
Given quadratic equation is,
x ² + 2√2x – 6 = 0
⇒ x ² + 3√2x – √2x – 6 = 0
⇒ x(x + 3√2) – √2(x + 3√2) = 0
⇒ (x + 3√2)(x – √2) = 0
⇒ (x + 3√2) = 0 or x – √2 = 0
⇒ x = -3√2 or x = √2
OR
Given quadratic equation is,
2x ² + ax – a ² = 0
⇒ 2x ² + 2ax – ax – a ² = 0
⇒ 2x (x + a) – a (x + a) = 0
⇒ (2x – a) (x + a) = 0
⇒ x = \(\frac{1}{2}\), x = – a

Question 23.
If cos α = \(\frac{1}{2}\) and tan β = \(\frac{1}{\sqrt{3}}\), then find sin (α + β), where α and β are both acute angles. [2]
Answer:

Or

Find an acute angle θ, when
\(\frac{\cos \theta-\sin \theta}{\cos \theta+\sin \theta}\) = \(\frac{1-\sqrt{3}}{1+\sqrt{3}}\) [2]
Answer:

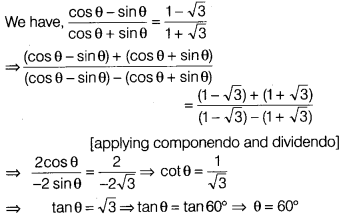
Alternate Method
We have, \(\frac{\cos \theta-\sin \theta}{\cos \theta+\sin \theta}\) = \(\frac{1-\sqrt{3}}{1+\sqrt{3}}\)
⇒ \(\frac{\frac{\cos \theta-\sin \theta}{\cos \theta}}{\frac{\cos \theta+\sin \theta}{\cos \theta}}\) = \(\frac{1-\sqrt{3}}{1+\sqrt{3}}\)
[dividing numerator and denominator by cos θ]
⇒ \(\frac{1-\tan \theta}{1+\tan \theta}\) = \(\frac{1-\sqrt{3}}{1+\sqrt{3}}\)
⇒ 1 + \(\sqrt{3}\) – tan θ – \(\sqrt{3}\)tan θ = 1 + tan θ – \(\sqrt{3}\) – \(\sqrt{3}\)tan θ
⇒ 2tan θ = 2\(\sqrt{3}\)
⇒ tan θ = \(\sqrt{3}\) ⇒ tan θ = tan 60°
⇒ θ = 60°

Question 24.
Find the coordinates of point A, where AB is diameter of a circle whose centre is (2, -3) and B is the point (1, 4).
Solution:

Let the coordinates of point A be (x, y) and point O (2, – 3) be the centre, then
By mid-point formula, \(\frac{x+1}{2}\) = 2 and \(\frac{y+4}{2}\) = -3
or x = 4 – 1 and y = – 6 – 4
⇒ x = 3 and y = – 10
∴ The coordinates of point A are (3, – 10)

Question 25.
The short and long hands of a clock are 6 cm and 8 cm long, respectively. Then, find the sum of the distance travelled by their tips in 1 day. [take π = 22/7] [2]
Answer:
In 1 day, i.e. 24 h, short (hour) hand of the clock make 2 revolutions and long (minute) hand make 24 revolutions.
In 1 revolution, distance travelled by tip of hour hand = Circumference of circle of radius 6 cm = 2 × \(\frac{22}{7}\) × 6
In 1 revolution distance travelled by tip of minute hand = Circumference of circle of radius 8 cm = 2 × \(\frac{22}{7}\) × 8
∴ Sum of distances travelled by tips of both hand in 1 day = 2 × 2 × \(\frac{22}{7}\) × 6 + 24 × 2 × \(\frac{22}{7}\) × 8
= 2 × \(\frac{22}{7}\)(12 + 192)
= 2 × \(\frac{22}{7}\) × 204
= 1282.29 cm (approx).

Section C
(Section C consists of 6 questions of 3 marks each.)

Question 26.
Find the area of the minor segment of a circle of radius 14 cm, when its central angle is 60°. Also find the area of the corresponding major segment. [Use π = \(\frac{22}{7}\)]
Solution:
Let ACB be the given arc subtending an angle of 60° at the centre.

Here, r = 14 cm and θ = 60°.
Area of the minor segment ACBA = (Area of the sector OACBO) – (Area of ΔOAB)
= \(\frac{\pi r^2 \theta}{360^{\circ}}\) – \(\frac{1}{2}\)r ² sin θ
= \(\frac{22}{7}\) × 14 × 14 × \(\frac{60^{\circ}}{360^{\circ}}\) – \(\frac{1}{2}\) × 14 × 14 × sin 60°
= \(\frac{308}{3}\) – 7 × 14 × \(\frac{\sqrt{3}}{2}\) = \(\frac{308}{3}\) – 49√3 = 17.89 cm ²
Area of the major segment BDAB = Area of circle – Area of minor segment ACBA
= πr ² – 17.89
= \(\frac{22}{7}\) × 14 × 14 – 17.89
= 616 – 17.89 = 598.11 ≈ 598 cm ² .

Question 27.
If sin θ + sin ² θ = 1, then find the value of
cos ¹² θ + 3cos ^1o θ + 3cos ⁸ θ + cos ⁶ θ + 2 cos ⁴ θ + 2cos ² θ – 2. [3]
Answer:
Given sin θ + sin ² θ = 1
⇒ sinθ = 1 – sin2θ
⇒ sinθ = cos ² θ
Now, cos ¹² θ + 3cos ¹⁰ θ + 3cos ⁸ θ + cos ⁶ θ + 2cos ⁴ θ + 2cos ² θ – 2
= (cos ¹² θ + 3cos ¹⁰ θ + 3cos ⁸ θ + cos ⁶ θ) + 2(cos ⁴ θ + cos ² θ – 1)
= (cos ⁴ θ + cos ² θ) ³ + 2 (cos ⁴ θ + cos ² θ – 1)
[∵ a ³ + 3a ² b+ 3ab ² + b ³ = (a+ b) ³ ]
= (sin ² θ + cos ² θ) + 2(sin ² θ + cos ² θ – 1)
[∵ cos ² A = sinA ⇒ cos ⁴ A = sin ² A]
= 1 + 2(1 – 1) = 1

Question 28.
Prove that the parallelogram circumscribing a circle is a rhombus.
Solution:
Let ABCD be a parallelogram such that its sides touch a circle with centre O.
Now, we know that tangents to a circle from an exterior point are equal in length.
∴ AP = AS …… (i)
BP = BQ …… (ii)
CR = CQ …… (iii)
DR = DS …… (iv)

Adding equations (i), (ii), (iii) and (iv), we get
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
⇒ AB + AB = BC + BC (Since ABCD is a parallelogram AB = CD, BC = DA)
⇒ 2AB = 2BC
AB =BC
Thus, AB = BC = CD = AD
Hence, ABCD is a rhombus.

Question 29.
If α and β are zeroes of a quadratic polynomial x ² – 5, then form a quadratic polynomial whose zeroes are 1 + α and 1 + β. [3]
Answer:
Let p(x) = x ² – 5
To find the zeroes of p(x), put p(x) = 0.
∴ x ² – 5 = 0 ⇒ x = ±5
Let α = 5 and β = -5
Now, 1 + α = 1 + 5 = 6 and 1 + β = 1 – 5 = -4
Thus, 6 and -4 are the zeroes of new quadratic polynomial.
Therefore, the new quadratic polynomial will be (x – 6) (x + 4) or x ² – 2x – 24.

Or

Can the quadratic polynomial x ² + kx + k have equal zeroes for some odd integer k > 1? [3]
Answer:
Let the given polynomial be p(x) = x ² + kx + k.
On comparing it with ax ² + bx + c, we get a = 1, b = k and c = k
Let equal zeroes be α and α.
Then, sum of zeroes, α + α = \(\frac{-b}{a}\) = \(\frac{-k}{1}\)
[∵ sum of zeroes = \(-\left(\frac{\text { coefficient of } x}{\text { coefficient of } x^2}\right)\)]
⇒ 2α = \(\frac{-k}{1}\) ⇒ α = \(\frac{-k}{2}\)
and product of zeroes, α ∙ α = \(\frac{c}{a}\) = \(\frac{k}{1}\) ⇒ α ² = k
[∵ product of zeroes = \(=\frac{\text { constant term }}{\text { coefficient of } x^2}\)]
∴ \(\left(\frac{-k}{2}\right)^2\) = k
⇒ k ² – 4k = 0
⇒ k(k – 4) = 0 ⇒ k = 0 or 4
When k = 0, then p(x) = x ²
When k = 4, then p(x) = x ² + 4x + 4
∴ p(x) = (x – 0) ² or (x + 2) ²
So, zeroes of p(x) are 0, 0 or -2, -2.
[∵ (x – 0) ² = 0 ⇒ x = 0, 0
and (x + 2) ² = 0 ⇒ x = -2, -2]
Thus, the equal roots are possible only, when k is even.
Hence, the given quadratic polynomial has no equal zeroes for some odd integer k > 1.

Question 30.
A two-digit number is such that the product of its digits is 20. If 9 is added to the number, the digit interchange their places. Find the number.
Solution:
Let the ten’s digit be x and the unit’s digit be y.
Thus, the given number is (10x + y) and its reverse is (10y + x).
So, xy = 20
x = \(\frac{20}{y}\) ….. (i)
and 10x + y + 9 = 10y + x
⇒ 9x – 9y = – 9
⇒ x – y = – 1
⇒ \(\frac{20}{y}\) – y = – 1
⇒ 20 – y ² = – y
⇒ y ² – y – 20 = 0
⇒ y ² – 5y + 4y – 20 = 0
⇒ y(y – 5) + 4(y – 5) = 0
⇒ (y – 5)(y + 4) = 0
⇒ y = 5, -4
So, x = \(\frac{20}{5}\), –\(\frac{20}{4}\)
x = 4, -5
So, Thus, the number is 45 or – 54.

Question 31.
From a well-shuffled pack of 52 cards, few cards of same colour are missing. If P (drawing a red card) = 2/3 and P (drawing a black card) = 1/3, then which colour cards are missing and how many? [3]
Answer:
Since, the probability of drawing a black card is less than that of a red card, therefore black cards are missing.
Let x be the number of missing black cards.
Then, P (drawing a black card) = \(\frac{26-x}{52-x}\) = \(\frac{1}{3}\)
⇒ 78 – 3x = 52 – x
⇒ -3x + x = 25 – 78
⇒ -2x = -26
⇒ x = \(\frac{26}{2}\) = 13
Hence, 13 black cards are missing.

Section D
(Section D consists of 4 questions of 5 marks each.)

Question 32.
Show that the sum of an AP whose first term is a, the second term b and the last term c, is equal to \(\frac{(a+c)(b+c-2 a)}{2(b-a)}\).
The ratio of the 11th term to the 18th term of an AP is 2 : 3. Find the ratio of the 5th term to the 21st term and also the ratio of the sum of the first five terms to the sum of the first 21 terms.
Solution:
Given: a (first term) = a,
d = b – a, a _n = c
By the formula of nth term, a + (n – 1)d = c
(n – 1)(b – a) = (c – a)


OR
Let a be the first term and d be the common difference of an AP.
a ₁₁ : a ₁₈ = 2 : 3
⇒ \(\frac{a+10 d}{a+17 d}\) = \(\frac{2}{3}\)
⇒ 3a + 30d = 2a + 34d
⇒ 3a – 2a = 34d – 30d
⇒ a = 4d ………… (i)

Question 33.
Compute the Arithmetic Mean for the following data [5]

Marks obtained	Number of students
Less than 10	14
Less than 20	22
Less than 20	37
Less than 40	58
Less than 50	67
Less than 60	75

Answer:
The above data may be written as

Class	0-10	10-20	20-30	30-40	40-50	50-60
Frequency	14	8	15	21	9	8

Here, h = 10
Let assumed mean = midpoint of (30 – 40) = 35
Now, we form the table under

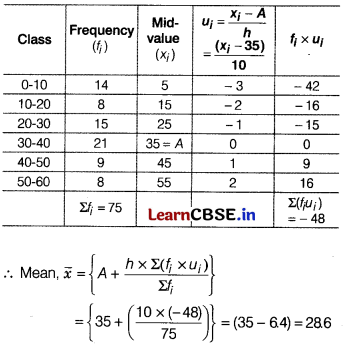
Question 34.
If sec θ + tan θ = p, show that: \(\frac{p^2-1}{p^2+1}\) = sin θ
Solution:
Given : Now, sec θ + tan θ = p

\(\frac{2 \tan \theta(\tan \theta+\sec \theta)}{2 \sec \theta(\tan \theta+\sec \theta)}\) = \(\frac{\tan \theta}{\sec \theta}\)
\(\frac{\sin \theta}{\cos \theta} \times \frac{\cos \theta}{1}\) = sin θ
R.H.S. Hence proved.

Question 35.
Find the solution of the following equation by factorization method.
\(\frac{x+1}{x-1}\) – \(\frac{x-1}{x+1}\) = \(\frac{5}{6}\), x ≠ 1, -1 [5]
Answer:
Given, equation is \(\frac{x+1}{x-1}\) – \(\frac{x-1}{x+1}\) = \(\frac{5}{6}\)
⇒ \(\frac{(x+1)^2-(x-1)^2}{(x+1)(x-1)}\) = \(\frac{5}{6}\)
⇒ \(\frac{x^2+1+2 x-\left(x^2+1-2 x\right)}{\left(x^2-1\right)}\) = \(\frac{5}{6}\)
⇒ 6[4x] = 5(x ² – 1)
⇒ 5x ² – 24x – 5 = 0
⇒ 5x ² – 25x + x – 5 = 0
[splitting middle term]
⇒ 5x(x – 5) + 1(x – 5) = 0
⇒ (x – 5)(5x + 1) = 0
⇒ x – 5 = 0 and 5x + 1 = 0
⇒ x = 5 and x = –\(\frac{1}{5}\) ….. (2)

Or

Solve the quadratic equation 9x ² – 9(a + b)x + (2a ² + 5ab + 2b ² ) = 0 by factorisation method.
Answer:
Given, quadratic equation is 9x ² – 9(a + b)x + (2a ² + 5ab + 2b ² ) = 0 … (i)
Now, 2a ² + 5ab + 2b ² = 2a ² + 4ab + ab + 2b ² = 2a(a + 2b) + b(a + 2b)
= (2a + b)(a + 2b)
∴ Eq. (i), can be rewritten as 9x ² – 9(a + b)x + (2a + b)(a + 2b) = 0
⇒ 9x ² – 3{(2a + b) + (a + 2b)}x + (2a + b)(a + 2b) = 0
⇒ 9x ² – 3(2a + b)x – 3(a + 2b)x + (2a + b)(a + 2b) = 0
⇒ 3x{3x – (2a + b)} – (a + 2b){3x – (2a + b)} = 0
⇒ {3x-(2a + b)}{3x-(a + 2b)} = 0
⇒ 3x – (2a + b) = 0 or 3x – (a + 2b) = 0
⇒ x = \(\frac{2 a+b}{3}\) or x = \(\frac{a+2 b}{3}\)

Section E
(Case Study Based Questions)
(Section E consists of 3 questions. All are compulsory.)

Question 36.
Sun casts a shadow on a nearby tree and building. If the height of building is √3 times the length of shadow and the angle of elevation of the top of building from its tip of shadow which is 160 m away from building is 60°. Based on the given data and answer the following questions :
(i) What is the angle of elevation of sun from tree?
(ii) What is the height of building?
(iii) If another building 80 m high casts a shadow of length 120 m. Find the angle of elevation.
OR
If the length of the shadow reduces from 160 m to 80 m and height of building remains same. Calculate the angle of depression of shadow tip from the top of building.
Solution:
(i) Given, height of building = √3 times × Length of shadow (l)
or h = √3 l
so, tan θ = \(\frac{\sqrt{3} l}{l}\)
or tan θ = √3
θ = 60° (∵ tan 60° = √3)

Question 37.
Sports Day
For a sports day celebration, the school decided to make activity between students in such a way that Vicky, Garvit and Shalini are standing at positions A, B and C whose coordinates are (3, 3), (5, 9) and (9, 3), respectively.

The teacher asked Deepanshi to fix the country flag at the mid-point of the line joining point A and B.

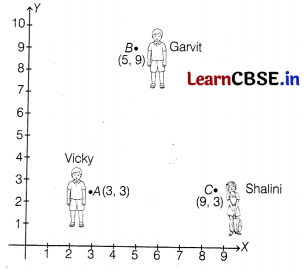
Based on above information, answer the following questions.
(i) Find the coordinates of the mid-point of line joining A and B. (1)
(ii) Find the distance between Garvit and Vicky. (1)
(iii) What is the space covered by these persons? (2)
Answer:
(i) Given points are A(3, 3) and B (5, 9).
Let Deepanshi fix the country flag at point D (x, y).
∴ x = \(\frac{3+5}{2}\) = \(\frac{8}{2}\) = 4 and y = \(\frac{3+9}{2}\) = \(\frac{12}{2}\) = 6
So, country flag is situated at point D(4, 6).

(ii) The distance between Gravit and Vicky
= \(\sqrt{(5-3)^2+(9-3)^2}\)
[∵ distance between two points = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)]
= \(\sqrt{(2)^2+(6)^2}\)
= \(\sqrt{4+36}\) = \(\sqrt{40}\)
= 2\(\sqrt{10}\) units

(iii) The space covered by three persons
= Area of ∆ABC
= \(\frac{1}{2}\)(base × height)
= \(\frac{1}{2}\) × (6 × 6) = \(\frac{36}{2}\)
= 18 sq units

Or

Find the point on the X-axis, which is equidistant from points A and C. (2)
Answer:
Let point on X-axis be P(x, 0)
Then, AP ² = CP ²
∴ (x – 3) ² + (0 – 3) ² = (x – 9) ² + (0 – 3) ²
⇒ x ² – 6x + 9 + 9 = x ² + 81 – 18x + 9
⇒ 12x = 72 ⇒ x = 6
Hence, point on X-axis is (6, 0).

Question 38.
Sita and Savita had 2 cubes of same dimension. They want to join the cubes as show in the figure.

The resulting shape is a cuboid. The side of the cube is 8 cm.
Answer the following questions:
(i) What are the dimensions of the resulting cuboid?
(ii) If the resulting cuboid, needs to be covered by a paper, how much area of paper is needed?
(iii) What is the volume of the resulting cuboid?
OR
If the cost of the paper is ?0.05/cm2. What is the total cost of the paper pasted on the cuboid? Solution:
(i) In resulting cuboid, length gets doubled, breadth and height remains same
Then l = 8 + 8 = 16 cm
b = 8 cm, h = 8 cm

(ii) Total surface area of cuboid = 2 (lb+ bh + hl)
= 2(16 × 8 + 8 × 8 + 16 × 8)
= 2 (128 + 64 + 128)
= 2 × 320 = 640 cm ²

(iii) Dimension of cuboid =16 cm, 8 cm, 8 cm
Volume of cuboid = lbh
= 16 × 8 × 8 = 1024 cm ²
OR
T.S.A. of paper used = 640 cm ²
Rate of paper = ₹0.05/cm ²
∴ Cost of paper = ₹640 × 0.05
= \(\frac{640 \times 5}{100}\) = ₹32