CBSE Sample Papers for Class 10 Maths Standard Set 10 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths with Solutions Set 10 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 10 with Solutions

Time: 3 hrs
Max. Marks: 80

Instructions

1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
(Section A consists of 20 questions of 1 mark each.)

Question 1.
If the mean of first n natural numbers is \(\frac{5 n}{9}\), then the value of n is (1)
(a) 5
(b) 7
(c) 9
(d) 0
Answer:
(c) 9

According to the given condition, mean of first n natural numbers = \(\frac{5 n}{9}\)

Question 2.
In the given figure, ΔABC ~ ΔPQR, find the measure of ∠C.

(a) 60°
(b) 40°
(c) 80°
(d) None of these
Answer:
(b) 40°
Explanation: Since,
ΔABC ~ ΔPQR
∠A = ∠P = 80° [Given]
⇒ ∠B = ∠Q – 60° [Given]
∠C = ∠R
By angle sum property, we have
∠A + ∠B + ∠C = 180°
⇒ 80° + 60° + ∠C = 180°
⇒ 140° + ∠C = 180°
⇒ ∠C = 180° – 140°
⇒ ∠C = 40°

Question 3.
The value of 2tan ² θ + cos ² θ – 2, if θ is an acute angle and sin θ = cos θ, is (1)
(a) 0
(b) 1
(c) –\(\frac{1}{2}\)
(d) \(\frac{1}{2}\)
Answer:
(d) \(\frac{1}{2}\)

Given, sinθ = cosθ
⇒ \(\frac{\sin \theta}{\cos \theta}\) = 1 ⇒ tanθ = 1
⇒ tanθ = tan 45° ⇒ θ = 45°
∴ 2tan ² θ + cos ² θ – 2 = 2tan ² 45° + cos ² 45° – 2
= 2(1) ² + \(\left(\frac{1}{\sqrt{2}}\right)^2\) – 2
= 2 × 1 + \(\frac{1}{2}\) – 2 = \(\frac{5}{2}\) – 2 = \(\frac{1}{2}\)

Question 4.
A tangent PQ at a point P to a circle of radius 5 cm meets a line through the centre O at a point Q, so that OQ = 13 cm, find PQ (in cm).
(a) 14
(b) 12
(c) 10
(d) None of these
Answer:
(b) 12
Explanation: Since tangent to a circle is perpendicular to radius.
So, ΔPOQ is right angled at P.
By Pythagoras theorem OQ ² = PQ ² + PO ²
⇒ (13) ² = (PQ) ² + (5) ²
⇒ 169 – 25 = (PQ) ²
⇒ 144 = PQ ²
⇒ PQ = \(\sqrt{144}\)
= 12 cm

Question 5.
In a rectangle ABCD, AB = 40 cm, ∠BAC = 30°, then the side BC is (1)
(a) \(\frac{40 \sqrt{3}}{3}\) cm
(b) \(\frac{20 \sqrt{3}}{3}\) cm
(c) \(\frac{20}{\sqrt{3}}\) cm
(d) None of these
Answer:
(a) \(\frac{40 \sqrt{3}}{3}\) cm

In ΔABC, we have AB =40 cm and ∠BAC = 30°

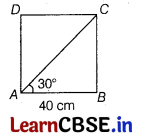
∴ tan 30° = \(\frac{B C}{A B}\) ⇒ \(\frac{1}{\sqrt{3}}\) = \(\frac{B C}{40}\)
⇒ BC = \(\frac{40}{\sqrt{3}}\) \(\frac{\sqrt{3}}{\sqrt{3}}\) = \(\frac{40 \sqrt{3}}{3}\) cm

Question 6.
Write the value of cot ² θ – \(\frac{1}{\sin ^2 \theta}\)
(a) -1
(b) 1
(c) 0
(d) None of these
Answer:
(a) – 1
Explanation: Given, cot ² θ – \(\frac{1}{\sin ^2 \theta}\)
⇒ cot ² θ – cosec ² θ [∵ cosec θ = \(\frac{1}{\sin \theta}\)]
⇒ – (cosec ² θ – cot ² θ)
⇒ -1 [∵ cosec ² θ – cot ² θ = 1)]

Question 7.
If the HCF of two numbers is 11 and their LCM is 693. If one of the numbers is 77, then the other number is (1)
(a) 99
(b) 33
(c) 112
(d) 94
Answer:
(a) 99

Let first number = 77
We know that
LCM × HCF = First number × Second number
⇒ Second number = \(\frac{11 \times 69}{77}\) = 99

Question 8.
A card is drawn from a well-shuffled deck of 52 playing cards. The probability that the card will not be an ace is:
(a) \(\frac{1}{13}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{12}{13}\)
(d) \(\frac{3}{4}\)
Answer:
(c) \(\frac{12}{13}\)
Explanation: Total number of possible outcomes = 52
Number of aces in the pack = 4
Thus, the probability of not drawing an ace
∴ P(E) = \(\frac{52-4}{52}=\frac{48}{52}=\frac{12}{13}\)

Question 9.
The HCF of two numbers p and q is 5 and their LCM is 200, then the product of pq is equal to (1)
(a) 100
(b) 1000
(c) 200
(d) 500
Answer:
(b) 1000

Given, HCF (p, q) = 5 and
LCM (p, g) = 200
∵ LCM × HCF = Product of two numbers
⇒ 5 × 200 = pq
⇒ pq = 1000

Question 10.
Two cubes each of 10 cm edge are joined end to end then what will be the surface area of the resulting cuboid?
(a) 100 cm ²
(b) 10000 cm ²
(c) 500 cm ²
(d) 1000 cm ²
Answer:
(d) 1000 cm ²
Explanation: Length of resulting cuboid = 20 cm
Breadth of resulting cuboid = 10 cm
Height of resulting cuboid =10 cm
Surface area of cuboid = 2(lb + bh + hi)
= 2(20 × 10 + 10 × 10 + 20 × 10)
= 2 [200 + 100 + 200]
= 2 × 500 = 1000 cm ²

Question 11.
If the circumference of a circle exceeds its diameter by 30 cm, then the radius of the circle is (1)
(a) 7 cm
(b) 8 cm
(c) 4 cm
(d) 6 cm
Answer:
(a) 7 cm

Let C be the circumference and d be the diameter.
Then, C = d + 30
⇒ 2π ᐧ \(\frac{d}{2}\) = (d + 30) ⇒ 2πd = 2d + 60
⇒ πd = d + 30 ⇒ d(π – 1) = 30
⇒ d\(\left(\frac{22-7}{7}\right)\) = 30 ⇒ d\(\left(\frac{15}{7}\right)\) = 30 ⇒ d = 7 × 2
∴ r = 7 cm

Question 12.
Write maximum value of \(\frac{1}{{cosec} \theta}\).
(a) \(\frac{1}{2}\)
(b) √2
(c) 1
(d) None of these
Answer:
(c) 1
Explanation: Maximum value of \(\frac{1}{{cosec} \theta}\) = sin θ = 1, when θ = 90°

Question 13.
If P(-2, 2) is the mid-point of the line segment joining A(-5, b) and B(b, 3), then the value of b is (1)
(a) 0
(b) -1
(c) 1
(d) 2
Answer:
(c) 1

Mid-point of A(-5, b) and B(b, 3) is \(\left(\frac{-5+b}{2}, \frac{b+3}{2}\right)\) = (-2, 2)
⇒ \(\frac{-5+b}{2}\) = -2
⇒ -5 + b = -4 ⇒ b = 5 – 4 = 1
and \(\frac{b+3}{2}\) ⇒ b = 4 – 3 = 1
∴ b = 1

Question 14.
How many real zeroes does the polynomial x ⁴ – 1 has?
(a) 3
(b) 4
(c) 1
(d) 2
Answer:
(d) 2
Explanation: Given polynomials is x ⁴ – 1
⇒ x ⁴ – 1 = (x ² – 1)(x ² + 1) [∵ a ² – b ² = (a – b)(a + b)]
⇒ x ⁴ – 1 = (x – 1)(x + 1)(x ² + 1)
So, x ⁴ – 1 has two real zeroes.

Question 15.
In a lottery ticket, there are 10 prizes and 25 blanks, the probability of not getting a prize is (1)
(a) \(\frac{7}{5}\)
(b) \(\frac{5}{7}\)
(c) 1
(d) 0
Answer:
(b) \(\frac{5}{7}\)

Total number of lottery ticket = 10 + 25 = 35
∴ P(not getting prize) = \(\frac{25}{35}\) = \(\frac{5}{7}\)

Question 16.
If t _n = n(n + 3), then difference of its 5 ^th term and 2 ^nd term is:
(a) 20
(b) 30
(c) -30
(d) 10
Answer:
(b) 30
Explanation: t _n = n(n + 3)
∴ t ₅ = 5(5 + 3) = 40
∴ t ₂ = 2(2 + 3) = 10
∴ t ₅ – t ₅ = 40 – 10 = 30

Question 17.
\(\frac{1+\cot ^2 A}{1+\tan ^2 A}\)is equal to (1)
(a) tan ² A
(b) sec ² A
(c) cot ² A
(d) 1 – sin ² A
Answer:
(c) cot ² A

we have, \(\frac{1+\cot ^2 A}{1+\tan ^2 A}\)
= \(\frac{1+\cot ^2 A}{1+\frac{1}{\cot ^2 A}}\) [∵ tanθ = \(\frac{1}{\cot \theta}\)]
= \(\frac{\cot ^2 A\left(1+\cot ^2 A\right)}{\cot ^2 A+1}\) = cot ² A

Question 18.
In the given figure, QR is parallel to AB and DR is parallel to QB. What is the number of distinct pairs of similar triangles?

(a) 1
(b) 2
(c) 3
(d) 4
Ans.
(b) 2
Explanation: QR is parallel to AB.
According to basic proportionality theorem,
\(\frac{\mathrm{PQ}}{\mathrm{PA}}\) = \(\frac{\mathrm{PR}}{\mathrm{PB}}\) ……… (1)
ΔPQR ~ ΔPAB

DR is also parallel to QB. [Given]
According to basic proportionality theorem,
\(\frac{\mathrm{PD}}{\mathrm{PQ}}\) = \(\frac{\mathrm{PR}}{\mathrm{PB}}\) ……… (2)
ΔPDR ~ ΔPQB
Therefore, there are two distinct pair of similar triangles in the given figure.

Directions In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) The distance of a points P (x, y) from the origin is \(\sqrt{x^2-y^2}\).
Reason (R) If P(-1, 1) is the mid-point of the line segment joining A(-3, b) and B(1, b + 4), then value of b is -1. (1)
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true but Reason (R) is false
(d) Assertion (A) is false but Reason (R) is true
Answer:
(d) Assertion (A) is false but Reason (R) is true

The distance of point P(x, y)from origin
= \(\sqrt{(x-0)^2+(y-0)^2}\)
= \(\sqrt{x^2+y^2}\)
Mid-point of A(-3, b) and B(1, b + 4) is
\(\left(\frac{-3+1}{2}, \frac{b+b+4}{2}\right)\) = (-1, b + 2)
Hence, Assertion is false but Reason is true.

Question 20.
Statement A (Assertion): If two tangent segments are drawn to one circle from the same external point, then they are congruent.
Statement R (Reason): If a line touches a circle, then perpendicular distance of the line from the centre of the circle is equal to the radius of the circle.
Answer:
(b) Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A).
Explanation: As per the two-tangent theorem, if two tangent segments are drawn to one circle from the same external point, then they are congruent. So, the assertion is proved to be correct. For this reason, as per the tangent to a circle theorem “A line is tangent to a circle if and only if s the line is perpendicular to the radius drawn to the point of tangency.” So, the statement in the reason is also true. But they don’t support or define each other.

Section B
(Section B consists of 5 questions of 2 marks each.)

Question 21.
One root of the quadratic equation 2x ² – 8x – k – 0 is 5/2. Find the other root and the value of k. (2)
Answer:
Given, 5/2 is one of the roots of the equation
2x ² – 8x – k = 0
On putting x = \(\frac{5}{2}\) in Eq.(i), we get
2(\(\frac{5}{2}\)) ² – 8(\(\frac{5}{2}\)) – k = 0
⇒ \(\frac{50}{4}\) – \(\frac{40}{2}\) – k = 0 ⇒ \(\frac{50-80-4 k}{4}\) = 0
⇒ -30 – 4k = 0
⇒ 4k = -30
⇒ k = \(\frac{-30}{4}\) = \(\frac{-15}{4}\)
Now, putting the value of k in Eq. (i), we get
2x ² – 8x + \(\frac{15}{2}\) = 0
⇒ 4x ² – 16x + 15 = 0
⇒ 4x ² – 6x – 10x + 15 = 0 [by factorisation]
⇒ 2x (2x – 3) – 5 (2x – 3) = 0
⇒ (2x – 5) (2x – 3) = 0
∴ x = \(\frac{5}{2}\) or \(\frac{3}{2}\)
Hence, the other root is \(\frac{3}{2}\) and the value of k is –\(\frac{15}{2}\).

Or

Using quadratic formula, solve for x
9x ² – 3(a + b)x + ab = 0.
Answer:
Given, equation is 9x ² – 3(a + b)x + ab = 0.
On comparing it with standard form
Ax ² + Bx + C = 0, we get
A = 9, B = -3(a + b) and C = ab
Discriminant, D = B ² – 4AC
= 9(a + b) ² – 4(9)(ab)
= 9{(a + b) ² – 4ab}
= 9(a – b) ² ≥ 0
[∵ (a + b) ² – 4ab = (a – b) ² ]

Therefore, the two real roots of the equation are given by

Hence, the two roots are \(\frac{a}{3}\) and \(\frac{b}{3}\).

Question 22.
Find whether the following system of equations is consistent or inconsistent:
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y = 7 and 9x – 10y = 14.
Solution:
We have,
\(\frac{3}{2}\)x + \(\frac{5}{3}\)y – 7 = 0
and 9x – 10y – 14 = 0
Here, a ₁ = \(\frac{3}{2}\), b ₁ = \(\frac{5}{3}\) c ₁ = -7
a ₂ = 9, b ₂ = -10, c ₂ = -14
Thus \(\frac{a_1}{a_2}=\frac{3}{2 \times 9}=\frac{1}{6}, \frac{b_1}{b_2}=\frac{5}{3(-10)}=-\frac{1}{6}\)
Since \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
So, given system of equations has unique solution and it is consistent.

Question 23.
If ΔABC – ΔDEF such that DE = 6 cm, EF = 4 cm, DF = 5 cm and BC = 8 cm, then find perimeter of ΔABC. (2)
Answer:
Given, ΔABC ~ ΔDEF
and DE = 6 cm, EF = 4 cm, DF = 5 cm
and BC = 8 cm

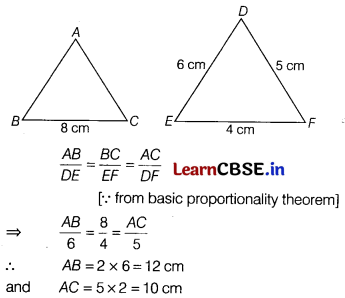
Now, perimeter of ΔABC = AB + BC + CA
= 12 + 8 + 10 = 30 cm

Question 24.
Find the 15 ^th term from the last term of the A.P.: 3, 8, 13, …, 253.
OR
Find the sum of all multiples of 7 lying between 500 and 900.
Sol. Given A.P. is 3, 8,13,…, 253.
Here, a = 3, d = 8 – 3 = 5, l = 253
We know that, nth term from last = l – (n -1 )d
∴ 15th term from last = 253 – (15 -1)5
= 253 – 70
⇒ = 183
Multiples of 7 lying between 500 and 900 are
504, 511, 518, 525,…, 896
We observe that the above series is an A.P.
∴ a = 504, d = 7, a _n = 896
Now, we know that,an = a _n + (n – 1 )d
⇒ 896 = 504 + (n – 1) 7
⇒ 392 = 7(n – 1)
⇒ n – 1 = 56
⇒ n = 57
Thus, S ₅₇ = \(\frac{57}{2}\) [504 + 896] [∵ S _n = \(\frac{n}{2}\) (a + l)]
\(\frac{57}{2}\) × 1400
= 57 × 700 = 39900

Question 25.
In the given figure, PT and PS are tangents to a circle from a point P, such that PT = 4 cm and ∠TPS = 60°. Find the length of chord TS. How many lines of same length TS can be drawn in the circle? (2)

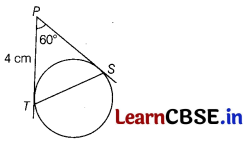
Answer:
We know that, tangents drawn from external point to the circle are equal in length.
Here, P is an external point.
∴ PS = PT = 4 cm
So, ∠PTS = ∠PST
[∵ angle opposite to equaP sides are equal]
∠PTS + ∠PST + ∠TPS = 180°
[by angle sum property of triangle]
⇒ ∠PTS + ∠PTS + 60° = 180°
[∵ ∠PST = ∠PTS and ∠TPS = 60°].
⇒ 2∠PTS = 180° – 60°
⇒ 2∠PTS = 120°
⇒ ∠PTS = \(\frac{120^{\circ}}{2}\) = 60°
∴ ΔPTS is an equilateral triangle.
Hence, TS = 4 cm
Here, infinite lines of same length TS can be drawn in a circle.

Or

AB is a diameter and AC is a chord of a circle such that ∠BAC = 30°. If the tangent at C intersects AB produced at D, prove that BC = BD.
Answer:
Given AB is a diameter of the circle with centre O and DC is the tangent of circle and ∠BAC = 30°.
To prove BC = BD
Construction Join O to C.

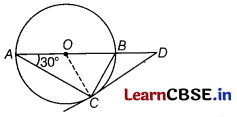
Proof Since, OC ⊥ CD
[∵ the tangent at any point of a circle is perpendicular to the radius through the point of contact]
∴ ∠OCB + ∠BCD = 90°
Now, OC = OA [radii]
⇒ ∠OCA = ∠OAC [angles opposite to equal sides are equal]
∴ ∠OCA = 30°
Now, ∠ACB = 90° [angle on a semi-circle]
∴ ∠OCA + ∠OCB = 90°
⇒ ∠OCB = 60° and ∠BCD = 30°
In ΔACD, ∠ACD + ∠CAD + ∠ADC = 180°
⇒ 120° + 30° + ∠ADC = 180°
⇒ ∠ADC = 30°
∴ In ΔBCD, ∠BCD = ∠BDC = 30°
[angles opposite to equal sides are equal]
∴ BC = BD Hence proved.

Section C
(Section C consists of 6 questions of 3 marks each.)

Question 26.
One card is chosen from a well-shuffled deck of 52 cards. Calculate the probability of getting :
(i) A non-ace
(ii) Neither a king nor a jack.
Solution:
Total number of cards = 52
(i) Let, E be the event that chosen card is a non-ace.
Number of non-ace cards = 52 – 4 = 48
Thus, P(E) = \(\frac{\text { Number of non-ace cards }}{\text { Total number of cards }}\)
= \(\frac{48}{52}\)
= \(\frac{12}{13}\)

(ii) Let, E be the event that chosen card is neither a king nor a jack.
Number of cards in which there is neither a king nor a jack = 52 – 8 = 44
Thus, P(E) = \(\)
= \(\frac{44}{52}\)
= \(\frac{11}{13}\)

Question 27.
From a bus stand in Delhi, if we buy 2 tickets to Pitampura and 3 tickets to Dilshad Garden, the total cost is ₹ 46 but if we buy 3 tickets to Pitampura and 5 tickets to Dilshad Garden, the total cost is ₹ 74. Then, find the fares from the bus stand to Pitampura and to Dilshad Garden. (3)
Answer:
Let fare from bus stand to Pitampura be ₹ x and to Dilshad Garden be ₹ y.
According to the question, we have
Cost of 2 tickets to Pitampura + 3 tickets to Dilshad Garden = ₹ 46
∴ 2x + 3y = 46 ……..(i)
and cost of 3 tickets to Pitampura + 5 tickets to Dilshad Garden = ₹ 74
and 3x + 5y = 74 …….(ii)
Multiplying Eq. (i) by 3 and Eq. (ii) by 2, we get
6x + 9y = 138 ………(iii)
and 6x + 10y = 148 …………..(iv)
Subtracting Eq. (iii) from Eq. (iv), we get
y = 10
From Eq. (i),
2x + 3(10) = 46 ⇒ 2x + 30 = 46
⇒ 2x = 16
⇒ x = 8
Hence, the fare from the bus stand in Delhi to Pitampura is ₹ 8 and the fare to Dilshad Garden is ₹ 10.

Question 28.
If one zero of the polynomial 2x ² + 3x + λ is \(\frac{1}{2}\), then find the value of λ and other zero.
Solution:
Let P(x) = 2x ² + 3x + λ
Its one zero is \(\frac{1}{2}\)
So, P(\(\frac{1}{2}\)) = 0
⇒ 2(\(\frac{1}{2}\)) ² + 3(\(\frac{1}{2}\)) + λ = 0
⇒ \(\frac{1}{2}\) + \(\frac{3}{2}\) + λ = 0
⇒ \(\frac{4}{2}\) + λ = 0
⇒ 2 + λ = 0
⇒ λ = -2
Let other zero be α. Then,
α + \(\frac{1}{2}\) = \(\frac{-3}{2}\)
⇒ α = \(\frac{-3}{2}\) – \(\frac{1}{2}\) = -2
Hence, λ = -2 and the other zero is -2.

Question 29.
Find a quadratic polynomial whose zeroes are reciprocals of the zeroes of the polynomial f(x) = ax ² + bx + c, a ≠ 0, c ≠ 0. (3)
Answer:
Let α and β be the zeroes of the polynomial
f(x) = ax ² + bx + c
Then, α + β = –\(\frac{b}{a}\) = αβ = \(\frac{c}{a}\)
Let S and P denote respectively, the sum and product of the zeroes of a polynomial whose zeroes are \(\frac{1}{\alpha}\) and \(\frac{1}{\beta}\)
∴ The required polynomial g(x) is given by
g(x) = k(x ² – Sx + P) = k(x ² + \(\frac{b}{c}\)x + \(\frac{a}{c}\)x)
where k is any non-zero constant.

Or

If α, β are the zeroes of the polynomial p(x) = 2x ² + 5x + k satisfying the relation α ² + β ² + αβ = \(\frac{21}{4}\), then find the value of k for this to be possible.
Answer:
Given, α and β are zeroes of polynomial p(x) = 2x ² + 5x + k.

Question 30.
In the given figure, XP and XQ are two tangents to the circle with centre O drawn from an external point X. ARB is another tangent touching the circle at R. Prove that XA + AR = XB + BR.

As XP and XQ are two tangents from X, so
XP = XQ ……. (i)
Also, AP = AR [Tangents from the external point A] …… (ii)
and BR = BQ [Tangents from the external point B] …… (iii)
Now, XP = XQ [from (i)]
⇒ XA + AP = XB + BQ
⇒ XA + AR = XB + BR [from (ii) and (iii)]
Hence Proved.

Question 31.
If the point R (x, y) is equidistant from the points P(a + b, a – b)and Q(b – a, a + b), then find distance of P from origin, mid-point of PQ and also prove that xa = yb. (3)
Answer:
P(a + b, a – b) be the given points and O(0, 0) be the origin
∴ OP = \(\sqrt{(a+b-0)^2+(a-b-0)^2}\) [by distance formula]
= \(\sqrt{(a+b)^2+(a-b)^2}\)
= \(\sqrt{a^2+b^2+2 a b+a^2+b^2-2 a b}\) = \(\sqrt{2\left(a^2+b^2\right)}\)
Mid-point of PQ
= \(\left(\frac{a+b+b-a}{2}, \frac{a-b+a+b}{2}\right)\)
= (b, a) [by mid-point formula]
Given, R (x, y) is equidistant from the points P (a + b, a – b) and Q (b – a, a + b), i.e. we have
PR = QR
⇒ \(\sqrt{[x-(a+b)]^2+[y-(a-b)]^2}\) = \(\sqrt{[x-(b-a)]^2+[y-(a+b)]^2}\) [by distance formula]
On squaring both sides, we get
(x – a – b) ² + (y – a + b) ² = (x – b + a) ² + (y – a – b) ²
⇒ x ² + a ² + b ² – 2xa + 2ab – 2xb + y ² + a ² + b ² – 2ya – 2ab + 2yb
= x ² + b ² + a ² – 2xb – 2ab + 2xa + y ² + a ² + b ² – 2ya + 2ab – 2yb
[∵ (x + y + z) ² = x ² + y ² + z ² + 2xy + 2yz + 2zx]
∴ -2xa + 2yb = 2xa – 2yb ⇒ 4yb = 4xa
⇒ xa = yb Hence proved.

Section D
(Section D consists of 4 questions of 5 marks each.)

Question 32.
Two ships are there in the sea on either side of a lighthouse in such a way that the ships and the lighthouse are in the same straight line. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45°. If the height of the lighthouse is 200 m, find the distance between the two ships. [Use √3 = 1.73]
Solution:
Given, the height of the lighthouse AC is 200 m. Let the distance of the first ship B from the lighthouse be x m and the distance of the second ship D from the lighthouse be y m.
Since the angle of depression is 60° for the first ship.

In ΔABC, we have
tan 60° = \(\frac{200}{x}\)
⇒ √3 = \(\frac{200}{x}\)
⇒ x = \(\frac{200}{\sqrt{3}}\)
Also, as the angle of depression is 45° with the second ship.
In ΔACD, we have
tan 45° = \(\frac{200}{y}\)
⇒ 1 = \(\frac{200}{y}\)
⇒ y = 200 m ……….. (ii)
Thus, from equations (i) and (ii), the distance between the two ships is
x + y = \(\frac{200}{\sqrt{3}}\) + 200
= 200(1 + \(\frac{1}{\sqrt{3}}\)) = 200(\(\frac{\sqrt{3}+1}{\sqrt{3}}\))
200(\(\frac{1.73+1}{1.73}\)) = 200(\(\frac{2.73}{1.73}\))
= 200(1.578)
= 315.6

Question 33.
Find the unknown entries m, n, o, p, q, and r in the following distribution of heights of students in a class. The total number of students is 50. (5)

Height (in cm)	150 – 155	155 – 160	160 – 165	165 – 170	170 – 175	175 – 180
Frequency	12	n	10	P	q	2
Cumulative frequency	m	25	0	43	48	r

Answer:
Given, distribution table is

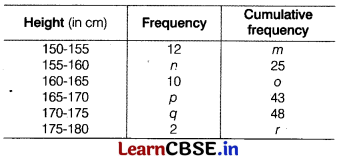
We know that the cumulative frequency of an interval is equal to the sum of the frequency of that interval and previous intervals.
Here, m = 12
∴ m + n = 25
⇒ 12 + n = 25
⇒ n = 25 – 12
⇒ n = 13
and 25 + 10 = o
⇒ o = 35
Also, 0 + p = 43
⇒ 35 + p = 43
⇒ p = 43 – 35 = 8
and 43 + q = 48
⇒ q = 48 – 43 = 5
and 48 + 2 = r ⇒ r = 50
Hence, the required values are m = 12, n = 13, 0 = 35, p = 8, q = 5 and r = 50.

Or

The following table gives the wages of workers in a factory.

Wages (in ₹)	Number of workers
45 – 50	5
50 – 55	8
55 – 60	30
60 – 65	25
65 – 70	14
70 – 75	12
75 – 80	6

Calculate the mean by the step deviation method.
Answer:
Let assumed mean, A = 62.5
To make a table for the product of frequency and step deviation

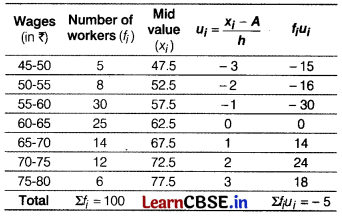
We know that
Mean \((\bar{x})\) = A + \(\frac{\Sigma f_i u_i}{\Sigma f_i}\) × h = 62.5 + \(\frac{(-5) \times 5}{100}\)
= 62.5 – 0.25 = 62.25
Hence, the mean wages are ₹ 62.25.

Question 34.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{OD}}\) Show that ABCD is a trapezium.
OR
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting AC at L and AD produced at E and AD = DE. Prove that EL = 2BL.
Solution:
Let EO || DC meet AD at E.
So, in ΔADC, EO || DC

So, \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{AE}}{\mathrm{ED}}\) [Thales’ theorem] …… (i)
But \(\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{BO}}{\mathrm{OD}}\)
By (i) and (ii), [Given …… (ii)]
So, \(\frac{\mathrm{BO}}{\mathrm{OD}}=\frac{\mathrm{AE}}{\mathrm{ED}}\)
Hence, \(\frac{\mathrm{BO}}{\mathrm{OD}}=\frac{\mathrm{AE}}{\mathrm{ED}}\)
and BO, OD, AE and ED are line segments of ΔDAB.
So, EO || AB
But EO || DC
Thus, AB || DC [By converse of Thales’ theorem]
As there are only two parallel sides in this quadrilateral, it is a trapezium. Hence proved.
OR
In ΔBMC and ΔEMD, we have

∠1 = ∠2 [Vertically opposite angles]
MC = MD [M being the mid-point of CD]
∠BCM = ∠EDM [Alternate angles]
Thus, ΔBMC ≅ ΔEMD [by ASA]
⇒ BC = DE (cpct)
Again, BC = AD [Opposite sides of the parallelogram ABCD]
∴ BC = AD = DE
So, AE = AD + DE = 2BC …… (i)
Again, in ΔAEL and ΔCBL, ∠5 = ∠6 [Vertically opposite angles]
∠3 = ∠4 [Alternate angles]
So, ΔAEL ~ ΔCBL
∴ \(\frac{\mathrm{EL}}{\mathrm{BL}}=\frac{\mathrm{AE}}{\mathrm{BC}}=\frac{2 \mathrm{BC}}{\mathrm{BC}}\) = 2 [From (i)]
Thus, EL = 2BL. Hence proved.

Question 35.
Find the roots of the following equation \(\frac{1}{x+4}\) – \(\frac{1}{x-7}\) = \(\frac{11}{30}\), x ≠ -47. (5)
Answer:
Given, equation is \(\frac{1}{x+4}\) – \(\frac{1}{x-7}\) = \(\frac{11}{30}\), x ≠ -4, 7

On comparing it with standard quadratic equation ax ² + bx + c = 0, we get
a = 1, b = -3 and c = 2
By using quadratic formula, we get

Hence, the roots of the given equation are 2 and 1.

Or

Solve for x, 2\(\left(\frac{2 x+3}{x-3}\right)\) – 25\(\left(\frac{x-3}{2 x+3}\right)\) = 5
Answer:
Let \(\frac{2 x+3}{x-3}\) = y ……… (i)
Then, \(\frac{x-3}{2 x+3}\) = \(\frac{1}{y}\)
Therefore, the given equation reduces to 2y – 25\(\frac{1}{y}\) = 5 ⇒ 2y ² – 25 = 5y
⇒ 2y ² – 5y – 25 = 0 ⇒ 2y ² – 10y + 5y – 25 = 0
[by factorisation method]
⇒ 2y(y – 5) + 5(y – 5) = 0 ⇒ (y – 5)(2y + 5) = 0
⇒ y = 5 or y = \(\frac{-5}{2}\)
Now, putting y = 5 in Eq. (i), we get
\(\frac{2 x+3}{x-3}\) = \(\frac{5}{1}\)
⇒ 5x – 15 = 2x + 3
⇒ 3x = 18 ⇒ x = 6
Again, putting y = –\(\frac{5}{2}\) in Eq. (i), we get
\(\frac{2 x+3}{x-3}\) = –\(\frac{5}{2}\)
⇒ 5x + 15 = 4x + 6
∴ 9x = 9
⇒ x = 1
Hence, the values of x are 1 and 6.

Section E
(Case Study Based Questions)
(Section E consists of 3 questions. All are compulsory.)

Question 36.
Students of class X are on visit of Sansad Bhawan. Teacher assign them the activity to observe and take some pictures to analyses the seating arrangement between various MP and Speaker based on coordinate geometry. The staff tour guide explained various facts related to Math’s of Sansad Bhawan to the students, students were surprised when teacher ask them you need to apply coordinate geometry on the seating arrangement of MP’s and Speaker.

Calculate the following refer to the above image and graph.
Answer the following questions :
(i) Refer to the points D and C, find the distance between the points C and D, if the coordinates of C is (2, -2) and D is (-2, -3).
(ii) Refer to the points D, A and H, condition for collinearity of points DAH satisfy by relation.
OR
Refer to the points B and C, join BC. Mark a point P on BC and P divides the line segment ‘ BP k
B(l, 4) and C(2, -2) such as = \(\frac{\mathrm{BP}}{\mathrm{PC}}=\frac{k}{1}\), if P lies on the line x – y = – 8. Find the value of k.
(iii) Refer to the points F and E. Find the mid-point of the line segment joining by the points F(-4, 3) and E(12, 3).
Solution:

(i) Distance between C(2, -2) and D(-2, -3) is
CD = \(\sqrt{(-2-2)^2+(-3+2)^2}\)
CD = \(\sqrt{16+1}\)
CD = \(\sqrt{17}\)

(ii) DA + AH = DH
OR
Given that P divides the line segment joining B(l, 4) and C(2, -2) in the ratio k : 1 so the coordinates of P are (\(\frac{2 k+1}{k+1}, \frac{-2 k+4}{k+1}\))
P(\(\frac{2 k+1}{k+1}, \frac{-2 k+4}{k+1}\)) lies on the line segment x – y = -8
⇒ (\(\frac{2 k+1}{k+1}\)) – (\(\frac{-2 k+4}{k+1}\)) = -8
⇒ 2k + 1 + 2k – 4 = – 8k – 8
⇒ 12k = -5
⇒ k = \(\frac{-5}{12}\)

(iii) Given point F(-4, 3) and E(12, 3).
Coordinates of mid-point are (\(\frac{-4+12}{2}, \frac{3+3}{2}\)) ⇒ (4, 3)

Question 37.
Number of Tangents on a Circle
The number of tangents drawn from a point on a circle depends upon the position of the point concerning the circle.

Suppose O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm OT intersects the circle at E and AB is the tangent to the circle at E.

Based on the above information, answer the following questions.

(i) Find the length of the tangent at point T. (2)
Answer:
(i) Given, radius of circle OP = 5cm and OT = 13cm.
We know that tangent at any point of a circle is perpendicular to the radius through the point of contact.

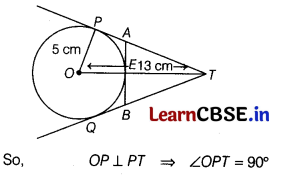
In right angled ΔOPT,
OT ² = OP ² + PT ²
[by Pythagoras theorem]
⇒ 13 ² = 5 ² + PT ²
⇒ PT ² = 169 – 25 = 144
∴ PT = 12 cm
[taking positive square root as length cannot be negative]

Or

Find the length of the tangent AB, if the length of the tangent at point T is 12 cm. (2)
(ii) How many tangents can be drawn from point O ? (1)
(iii) How many tangents can be drawn from point T? (1)
Answer:
Also, we know that lengths of tangents drawn from a point to a circle are equal.
Therefore, AP = AE = x (say)
Now, AT = PT – AP = (12 – x) cm
Since AB is tangent to the circle at point E and OE is the radius.
Therefore, OE ⊥ AB ⇒ ∠OEA = 90°
⇒ ∠AET = 90°
[∵ OT is a straight line, so ∠OEA + ∠AET = 180°]
Now, in right-angled ΔAET,
AT ² = AE ² + ET ²
[by Pythagoras theorem]
⇒ (12 – x) ² = x ² + (13 – 5) ²
[∵ ET =OT – OE = 13 – 5]
⇒ 144 – 24x + x ² = x ² + 64
[∵ (a – b) ² = a ² + b ² – 2ab]
⇒ -24x = -80 ⇒ x = \(\frac{10}{3}\) cm
⇒ AE = \(\frac{10}{3}\) cm
Similarly, BE = \(\frac{10}{3}\) cm
Hence, AB = AE + BE = \(\frac{10}{3}\) + \(\frac{10}{3}\) = \(\frac{20}{3}\) cm

(ii) No tangent can be drawn from point O.
(iii) 2 tangents can be drawn from point T.

Question 38.
Radha was very happy about her birthday. She got lots of presents on her birthday. Out of many birthday presents she liked the playing top the most. The shape of that top is like a cone which is surmounted by a hemisphere top as shown in the figure. The Top’ was painted with dull colours, now Radha want to make it more bright by colouring it with different colours. The height of the top is 7 cm diameter of hemisphere is 5.6 cm.

Answer the following questions :
(i) What is the surface area of hemispherical part, which is to be painted green?
(ii) If conical part need to be coloured bright orange. How much area need to be painted? (approx.)
(iii) Find the ratio of the height of the cone and hemispherical portion.
OR
What is the total cost of painting? If its cost ₹ 0.05 for 1 cm ² ?
Solution:
(i) Curved surface area of hemisphere = 2πr ²
= 2 × \(\frac{22}{7}\) × (\(\frac{5.6}{2}\)) ²
= 2 × \(\frac{22}{7}\) × 2.8 × 2.8
= 49.28 cm ²
= 50 cm ² (Approx)

(ii) C.S.A. of cone = πrl
= πr\(\sqrt{h^2+r^2}\)
Here, r = 2.8 cm, h = 7 – 2.8 = 4.2 m
∴ C.S.A. = \(\frac{22}{7}\) × 2.8\(\sqrt{(4.2)^2+(2.8)^2}\)
= 22 × 0.4 × \(\sqrt{17.64+7.84}\)
= 8.8 × \(\sqrt{25.48}\)
= 44.42 cm ²
= 45 cm ² (Approx)

(iii) Height of cone = 7 – 2.8 = 4.2 cm
Height of hemisphere = 2.8 cm (radius of cone)
∴ Ratio = \(\frac{4.2}{2.8}=\frac{6}{4}=\frac{3}{2}\)
OR
Total area to be painted = 45 + 50 = 95 cm ²
Cost = 95 × 0.05 = 4.75