CBSE Sample Papers for Class 10 Maths Standard Set 1 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Standard with Solutions Set 1 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Standard Set 1 with Solutions

Time: 3 hrs
Max. Marks: 80

Instructions:
1. This question paper has 5 Sections A-E.
2. Section A has 20 MCQs carrying 1 mark each.
3. Section B has 5 questions carrying 2 marks each.
4. Section C has 6 questions carrying 3 marks each.
5. Section D has 4 questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment (4 marks each).
7. All questions are compulsory. However, an internal choice in 2 questions of 2 marks, 2 questions of 3 marks and 2 questions of 5 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section A
Section-A consists of 20 Questions of 1 mark each

Question 1.
Which term of the AP 2, -1,-4 , -7, …… is -40 ? [1]
(a) 8th
(b) 11th
(c) 15th
(d) 23rd
Answer:
(c) 15th

Here, a = 2 and d = (-1 – 2) = – 3
Let a _n = – 40
Then, a + (n – 1)d = a _n
⇒ 2 + (n – 1) × (-3) = – 40
⇒ n = 15th

Question 2.
The given linear polynomial y = f(x) has

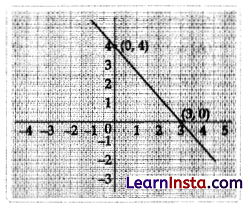
(A) 2 zeros
(B) 1 zero and the zero is ‘3’
(C) 1 zero and the zero is ‘4’
(D) No zero 1
Solution:
(B) 1 zero and the zero is ‘3’

Detailed Answer:
Polynomial y = f(x) intersects the x-axis at only one point, so the zero is one, and intersects the x-axis at point (3), so the zero of the polynomial y = f(x) is 3.

Question 3.
The area of the shaded portion is [1]

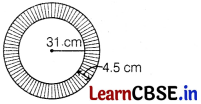
(a) 940.5 cm²
(b) 930.5 cm²
(c) 400.5 cm²
(d) 510.5 cm²
Answer:
(a) 940.5 cm²

Radius of smaller circle = 31 cm
Radius of larger circle = 31 + 4.5= 35.5 cm
∴ Area of path = [π(35.5)2 – π(31)2]
= π [(35.5) ² – (31) ² ]
= π (35.5 + 31) (35.5 – 31)
= π × 66.5 × 4.5
= \(\frac{22}{7}\) × 66.5 × 4.5= 940.5 cm²

Question 4.
The nature of roots of the quadratic equation 9x ² – 6x – 2 = 0 is:
(A) No real roots
(B) 2 equal real roots
(C) 2 distinct real roots
(D) More than 2 real roots 1
Solution:
(C) 2 distinct real roots

Detailed Answer:
Given quadratic equation is 9x ² – 6x – 2 = 0
9x ² – 6x – 2=0
a = 9
b = -6
c = -2
Now, b ² – 4ac
⇒ (-6) ² – 4 × 9 × (-2)
⇒ 36 + 72
b ² – 4ac = 0
So the roots is distinct real. Here, the given equation is of order 2, so there are two roots.

Question 5.
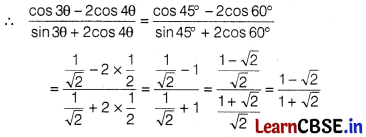
If θ = 15°, then \(\frac{\cos 3 \theta-2 \cos 4 \theta}{\sin 3 \theta+2 \cos 4 \theta}\) is equal to [1]
(a) \(\frac{1}{\sqrt{2}}\)
(b) \(\frac{1+\sqrt{2}}{1-\sqrt{2}}\)
(c) \(\frac{2+\sqrt{2}}{2-\sqrt{2}}\)
(d) \(\frac{1-\sqrt{2}}{1+\sqrt{2}}\)
Answer:
(d) \(\frac{1-\sqrt{2}}{1+\sqrt{2}}\)

Given, θ = 15°

Question 6.
What is the ratio in which the line segment joining (2,-3) and (5,6)is divided by the x-axis?
(A) 1:2
(B) 2:1
(C) 2:5
(D) 2:1
Solution:
(A) 1:2

Detailed Answer:

Question 7.
In a right-angled ∆ABC, right-angled at C, if tan A = 1, then the value of 2 sin A cos A, is [1]
(a) 0
(b) 1
(c) 2
(d) \(\frac{1}{2}\)
Answer:
(b) 1

We have, tan A = 1 ⇒ ∠A = 45°
∴ 2 sin A cos A = 2 sin45°cos45°
= 2 × \(\frac{1}{\sqrt{2}}\) × \(\frac{1}{\sqrt{2}}\) = \(\frac{1}{2}\) = 1

Question 8.

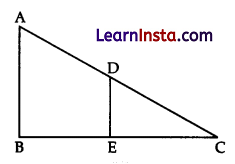
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is
(A) \(\frac{a c}{b}\)
(B) \(\frac{a c}{b+c}\)
(C) \(\frac{a b}{c}\)
(D) \(\frac{a b}{b+c}\)
Solution:
(B) \(\frac{a c}{b+c}\)

Detailed Answer:
Using basic proportional theorem.

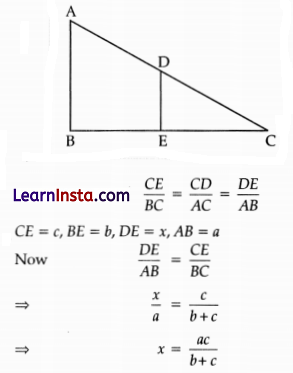
Question 9.
If 2x² + bx + 8 =0 to have non-real roots, then the interval for b is [1]
(a) -8 < b < 8
(b) -6 < b < 6 (c) -8 > b > 8
(d) None of these
Answer:
(a) -8 < b < 8

Given, 2×2 + bx+8 = 0 …(i)
We have, for non-real roots D < 0
⇒ b² – 4ac < 0
⇒ b² – 64 < 0
⇒ b² < 64
⇒ |b| < 8
⇒ b < 8 and b > -8
For -8 < b < 8, Eq. (i) has non-real roots.

Question 10.
A quadrilateral PQRS is drawn to circumscribe a circle.
If PQ = 12 cm, QR = 15cm and RS = 14 cm, find the length of SP is:
(A) 15cm
(B) 14cm
(C) 12cm
(D) 11cm
Solution:
(D) 11cm

Detailed Answer:

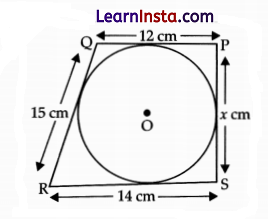
PQ + RS = PS + QR
12 + 14 = x + 15
26 – 15 = x
x = 11cm

Question 11.
If the common difference of an AP is 5, then the value of a ₁₈ – a ₁₃ is [1]
(a) 5
(b) 20
(c) 25
(d) 30
Answer:
(c) 25

Given, common difference of an AP, d = 5
Now, a ₁₈ – a ₁₃ = (a + 17d) – (a + 12d)
= a + 17d – a – 12d
= 5d = 5(5) = 25

Question 12.
(sec A + tan A) (1 – sin A) equals:
(A) sec A
(B) sin A
(C) cosec A
(D) cos A
Solution:
(D) cos A

Detailed Answer:
Since, (sec A + tan A) (1 – sin A)

= cos A

Question 13.
Suppose mean of 10 observations is 20, if we add 5 in each observation, then the new mean is [1]
(a) 25
(b) 10
(c) 20
(d) 5
Answer:
(a) 25

If we add 5 in each observation, then new mean will be 20 + 5 i.e. 25.

Question 14.
If the perimeter and the area of a circle are numerically equal, then the radius of the circle is:
(A) 2 units
(B) π units
(C) 4 units
(D) 7 units
Solution:
(A) 2 units

Detailed Answer:
Let radius of the circle be r
Given, perimeter of circle = Area of circle
2πr = πr ²
2 = r
r = 2 units

Question 15.
A solid ball is exactly fitted inside a cubical box of side a. The volume of the ball is [1]
(a) \(\frac{1}{6}\) πa ³
(b) \(\frac{4}{3}\) πa ³
(c) \(\frac{1}{3}\) πa ³
(d) None of these
Answer:
(a) \(\frac{1}{6}\) πa ³

Because a solid ball is exactly fitted inside the cubical box of side a. So, a is the diameter for the solid ball.
∴ Radius of the ball = \(\frac{a}{2}\)
So, volume of the ball = \(\frac{4}{3}\) π(\(\frac{a}{2}\)) ³ = \(\frac{1}{6}\) πa ³

Question 16.
There is a complete shaded square board of side ‘2a’ units circumscribing a shaded circle. Jayadev is asked to keep a dot on the above said board. The probability that he keeps the dot on the complete shaded region.
(A) \(\frac{\pi}{4}\)
(B) \(\frac{4-\pi}{4}\)
(C) \(\frac{\pi-4}{4}\)
(D) \(\frac{4}{\pi}\)
Solution:
(B) \(\frac{4-\pi}{4}\)

Detailed Answer:

Since, Total area of board = Area of complete shaded + Area of shaded region
= Area of square board (2a) ² = 4a ² unit ²
Radius of shaded circle = 2a/2 = 2
Now Area of complete shaded region = Area of square board – Area of shaded circle
= 4a ² – πa ²
= a ² (4 – π)
Required probability = \(\frac{\text { Area of complete shaded region }}{\text { Total area }}\)
= \(\frac{a^2(4-\pi)}{4 a^2}=\frac{4-\pi}{4}\)

Question 17.
Write the value of k for which the system of equations x + ky = 0 and 2x – y = 0 has unique solution. [1]
(a) k = \(\frac{1}{2}\)
(b) k = \(– \frac{1}{2}\)
(c) k ≠ \(\frac{-1}{2}\)
(d) k ≠ \(\frac{1}{2}\)
Answer:
(c) k ≠ \(\frac{-1}{2}\)

Given system of equations,
x + ky = 0 and 2x – y = 0
On comparing these equations with
a ₁ x + b ₁ y + c ₁ = 0 and a ₂ x + b ₂ y + c ₁ = 0, we get
a ₁ = 1, b ₁ =k, c ₁ = 0
and a ₂ =2, b ₂ = -1, c ₂ = 0
Condition for unique solution,
\(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)
⇒ \(\frac{1}{2} \neq \frac{k}{-1}\)
⇒ k ≠ \(\frac{-1}{2}\)

Question 18.
The upper limit of the modal class of the given distribution is:

(A) 165
(B) 160
(C) 155
(D) 150
Solution:
(D) 150

Detailed Answer:

Class	Frequency
135-140	4
140-145	7
145-150	18
150-155	11
155-160	6
160-165	5

Higher frequency is 18 then modal class is 145 – 150.
The upper limit at modal class is 150.

Question 19.
Assertion (A): All regular polygons of the same number of sides such as equilateral triangles, squares, etc. are similar.
Reason (R): Two polygons are said to be similar if their corresponding angles are equal and the lengths of corresponding sides are proportional.
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A)
(c) Assertion (A) is true but Reason (R) is false
(d) Assertion (A) is false but Reason (R) is true
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A)

Two polygons are similar if their corresponding angles are equal and sides are proportional.
∵ In equilateral triangle and square, each angle are equal and sides are also proportional therefore, regular polygons are similar.
Hence, both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

Question 20.
Statement A (Assertion): -5, \(\frac{-5}{2}\), 0, \(\frac{5}{2}\), …. is in Arithmetic Progression.
Statement R (Reason): The terms of an Arithmetic Progression cannot have both positive and negative rational numbers.
(A) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A)
(B) Both assertion (A) and reason (R) are true and reason (R) is not the correct explanation of assertion (A)
(C) Assertion (A) is true but reason (R) is false.
(D) Assertion (A) is false but reason (R) is true.
Solution:
(C) Assertion (A) is true but reason (R) is false.

Detailed Answer:

Hence, common difference is equal each term so this series is A.P. So, assertion is true.
Reason: The term of A.E have also negative and positive rational number, so reason is false.

Section B
(Section-B consists of 5 Questions of 2 marks each)

Question 21.
Prove that
(cosec A – sin A) (sec A – cos A) = \(\frac{1}{tan A + cot A}\)
Or
If cos θ + sin θ = √2 cos θ, then prove that cos θ – sin θ = √2 sin θ. [2]
Solution:
LHS = (cosec A – sin A) (sec A – cos A)

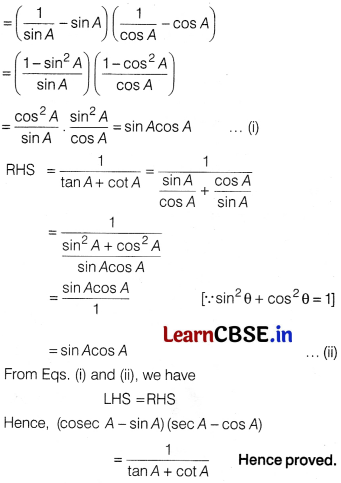
Or

Let cos θ – sin θ = x …(i)
Given, cos θ + sin θ = √2 cos θ …….(ii)
On squaring Eqs. (i) and (ii) and adding, we get
cos²θ + sin²θ – 2 cos0 ⋅ sin0 + cos²θ + sin²θ + 2 cosθ ⋅ sinθ = x² + 2 cos²θ
⇒ 1 + 1 = x² + 2 cos²θ
⇒ 2 = x² + 2(1 – sin²θ)
⇒ 2 = x² + 2 – 2 sin²θ
⇒ x² = 2 sin²θ
⇒ x = √2 sin θ
Hence, cos θ – sin θ = √2 sin θ

Alternate :

Given, cos θ + sin θ = √2 cos θ
sin θ = √2 cos θ – cos θ
⇒ sin θ = cos0(√2 – 1)
⇒ (√2 + 1) sin θ = cos θ (√2 – 1) (√2 + 1)
⇒ √2 sin θ + sinθ = cos θ(2 – 1)
⇒ √2 sin θ = cos θ – sin θ
Hence, cos θ – sin θ = √2 sin θ

Question 22.

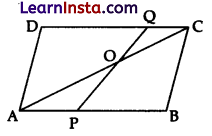
ABCD is a parallelogram. Point P divides AB in the ratio 2 : 3 and point Q divides DC in the ratio 4: 1.
Prove that OC is half of OA.
Solution:
ABCD is a parallelogram.

Question 23.
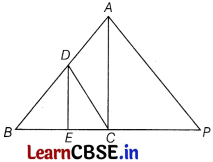
In given ∆ABC, DE || AC. If DC || AP, where point P lies on BC produced, then prove that \(\frac{B E}{E C}=\frac{B C}{C P}\).

Or
In ∆ABC and ∆DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, show that the two triangles are similar but not congruent. [2]
Sol. Given, in ∆ABC,
DE || AC [given]
So, \(\frac{B E}{E C}=\frac{B D}{D A}\) ……(i)
[by basic proportionality theorem]
DC || AP [given]
So, \(\frac{B C}{C P}=\frac{B D}{D A}\) ……..(ii)
[by basic proportionality theorem]
From Eqs. (i) and (ii), we get
\(\frac{B E}{E C}=\frac{B C}{C P}\)
Hence Proved.

Or

In ∆ABC and ∆DEF, we have ∠B = ∠E, ∠F = ∠C
⇒ ∆ABC ~ ∆DEF
[by AA similarity criterion]

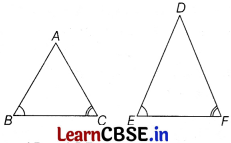
Since AB and DE are corresponding sides.
But AB = 3DE [given]
We know that two triangles are congruent,
if they have the same shape and size.
But here, AB = 3DE i.e. two triangles are not of same size.
∴ ∆ABC is not congruent to ∆DEF.
Hence, the two triangles are similar but not congruent.

Question 24.
(A) If tan (A + B) = √3 and tan (A-B) = = \(\frac{1}{\sqrt{3}}\); 0° < A + B < 90°; A>B, find A and B.
Solution:
∵ tan(A + B) = √3
∴ A + B = 60° … (i)
∵ tan(A – B) = \(\frac{1}{\sqrt{3}}\)
∴ A – B = 30 … (ii)
Adding (i) & (ii), we get 2A = 90°
⇒ A = 45°
Also (i) – (ii), we get 2B = 30°
⇒ B = 15°

OR

(B) Find the value of x if
2cosec ² 30° + x sin ² 60° – \(\frac{3}{4}\) tan ² 30° = 10
Solution:
2cosec ² 30° + x sin ² 60° – \(\frac{3}{4}\) tan ² 30° = 10
⇒ 2(2) ² + x (\(\frac{\sqrt{3}}{2}\)) ² – \(\frac{3}{4}\)(\(\frac{1}{\sqrt{3}}\)) ² = 10
⇒ 2(4) + x(\(\frac{3}{4}\)) – \(\frac{3}{4}\)(\(\frac{1}{3}\)) = 10
⇒ 8 + x(\(\frac{3}{4}\)) – \(\frac{1}{4}\) = 10
⇒ 32 + x(3) – 1 = 40
⇒ 3x = 9
⇒ x = 3

Question 25.
The students of a class are made to stand in rows. If 4 students are extra in each row, there would be 2 rows less. If 4 students are less in each row, there would be 4 rows more, then find the number of students in the class. [2]
Solution:
Let the number of rows = x
and the number of students in each row = y
Then, the total number of students = xy
When there are 4 more students in each row,
number of students in each row = y + 4
and number of rows = x – 2
Now, total number of students = (x – 2) (y + 4)
Given, (x – 2)(y + 4) = xy
⇒ 4x – 2y = 8
⇒ 2x – y = 4 … (i)
When 4 students are removed from each row, number of students in each row = (y – 4)
and number of rows = (x + 4)
Total number of students = (x + 4) (y – 4)
Given, {x + 4) (y – 4) = xy
⇒ 4y – Ax = 16
⇒ 4(y – x) = 16
⇒ y – x = 4 …(ii)
Adding Eqs. (i) and (ii), we get x = 8
On putting x = 8 in Eq. (ii), we get
y – 8 = 4 ⇒ y = 12
x = 8 and y = 12
Total number of students in the class = (12 × 8) = 96

Section C
(Section-C consists of 6 Questions of 3 marks each)

Question 26.
National Art convention got registrations from students from all parts of the country, of which 60 are interested in music, 84 are interested in dance and 108 students are interested in handicrafts. For optimum cultural exchange, organisers wish to keep them in minimum number of groups such that each group consists of students interested in the same art form and the number of students in each group is the same. Find the number of students in each group. Find the number of groups in each art form. How many rooms are required if each group will be allotted a room?
Solution:
Number of students in each group subject to the given condition = HCF (60, 84, 108)
HCE (60, 84, 108) = 12
Number of groups in Music = \(\frac{60}{12}\) = 5
Number of groups in Dance = \(\frac{84}{12}\) = 7
Number of groups in Handicrafts = \(\frac{108}{12}\) =9
Total number of rooms required = 21

Question 27.
Find the value(s) of k for which the following equations have equal roots (k – 12)x ² + 2(k – 12)x + 2 = 0 [3]
Solution:
Given quadratic equation is
(k – 12)x ² + 2(k – 12)x + 2 = 0
On comparing with ax ² + bx + c = 0, we get
a = k – 12, b = 2(k – 12) and c = 2
∴ D = b ² – 4ac = 4(k – 12) ² – 4(k – 12) × 2
= 4(k – 12)[k – 12 – 2]
= 4(k – 12)(k – 14)
The given equation will have equal roots, if
D = 0
⇒ 4(k – 12)(k – 14) = 0
⇒ (k – 12) = 0 and (k – 14) = 0
⇒ k = 12 and k = 14
Hence, the value of k is 12 and 14.

Question 28.
(A) The sum of a two-digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?
Solution:
Let the ten’s and the unit’s digits in the first number be x and y, respectively.
So, the original number = 10x + y
When the digits are reversed, x becomes the unit’s digit and y becomes the ten’s digit.
So the obtain by reversing the digits = 10y + x
According to the given condition.
(10x + y) + (10y + x) = 66
ie, 11(x + y) = 66
ie, x + y = 6 … (i)
We are also given that the digits differ by 2,
therefore, either x – y = 2 … (ii)
or y – x = 2 … (iii)
If x – y = 2, then solving (i) and (ii) by elimination,
we get x = 4 and y = 2.
In this case, we get the number 42.
If y – x = 2, then solving (i) and (iii) by elimination,
we get x = 2 and y = 4.
In this case, we get the number 24.
Thus, there are two such numbers 42 and 24.

OR

(B) Solve: \(\frac{2}{\sqrt{x}}\) + \(\frac{3}{\sqrt{y}}\) = 2; \(\frac{4}{\sqrt{x}}\) – \(\frac{9}{\sqrt{y}}\) = -1 x,y>0
Solution:
Let \(\frac{1}{\sqrt{x}}\) be ‘m’ and \(\frac{1}{\sqrt{y}}\) be ‘n’
Then the given equations become
2m + 3n = 2
4m – 9n = -1
(2m + 3m = 2) × – 2
⇒ -4m – 6n = -4 … (i)
4m – 9n = -1 … (ii)
Adding (i) and (ii)
We get, -15n = -5
⇒ n = \(\frac{1}{3}\)
Substituting n = \(\frac{1}{3}\) in 2m + 3n = 2, we get
2m + 1 = 2
2m = 1
m = \(\frac{1}{2}\)
√x = 2
x = 4 and n = \(\frac{1}{3}\)
√y = 3
y = 9

Question 29.
In the given figure, PQ is a chord of a circle and PT is tangent at P such that ∠QPT = 60°, then find the measure of ∠PRQ.

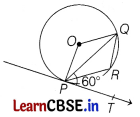
Solution:
Take a point Q’ on circle and join PQ’ and QQ’.

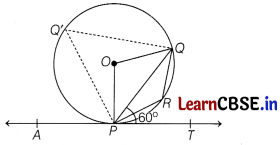
Now, ∠OPQ = 90° – 60° = 30°
[∵ ∠OPT = 90°, as radius OP is perpendicular to the tangent]
∠OQP = 30° [angles opposite to equal sides are equal]
In ∆OPQ, using the angle sum property of a triangle,
∠POQ + ∠OPQ + OQP = 180°
⇒ ∠POQ + 30°+ 30° =180°
⇒ ∠POQ = 180°- 60° = 120°
⇒ ∠PQ’Q = 60°
[The angle subtended by an arc at center is twice the angle subtended at the remaining part of the circle]
⇒ ∠PRQ = 180° – ∠PQ’Q = 180°- 60° = 120°
[∵ opposite angles are supplementary in a cyclic quadrilateral PQ’QR]

Question 30.
IF 1 + sin ² θ = 3 sin θ cos θ then prove that tan θ = 1 or 1/2.
Solution:
Given, 1 + sin ² θ = 3 sinθ cos θ
Dividing both sides by cos ² θ,
= \( \frac{1}{\cos ^2 \theta} \) + tan ² θ = 3 tan θ
sec ² θ + tan ² θ = 3 tan θ
1 + tan ² θ + tan ² θ = 3 tan θ
1 + 2 tan ² θ = 3 tan θ
2 tan ² θ – 3 tan θ + 1 = 0
If tan θ = x, then the equation becomes
2x ² – 3x + 1 = 0
⇒ (x – 1) (2x – 1) =0
x = 1 or \(\frac{1}{2}\)
tan θ = 1 lor \(\frac{1}{2}\)

Question 31.
If tan A = n tanB and sin A = m sin B, then prove that cos² A = \(\frac{m^2-1}{n^2-1}\)
Solution:
We have to find cos²A in terms of m and n . This means that ∠B is to be eliminated from the given relations.
Now, tan A = n tan B ⇒ tan B = \(\frac{1}{n}\) tan A

Section D
(Section-D consists of 4 Questions of 5 marks each)

Question 32.
(A) A motor boat whose speed is 18 km/h in still water takes 1 h. more to go 24 km upstream than to return downstream to the same spot. Find the speed of stream.
Solution:
Let the speed of the stream be x km/h.
The speed of the boat upstream = (18 – x) km/h and
The speed of the boat downstream = (18 + x) km/h.
The time taken to go upstream = \(\frac{\text { Distance }}{\text { Speed }}\)
= \(\frac{24}{18-x}\) hours
The time taken to go downstream = \(\frac{\text { Distance }}{\text { Speed }}\)
= \(\frac{24}{18+x}\) hours
According to the question,
\(\frac{24}{18-x}\) – \(\frac{24}{18+x}\) = 1
24(18 + x) – 24(18 – x) = (18 – x) (18 + x)
x ² + 48x – 324 =0
x = 6o or -54
Since x is the speed of the stream, it cannot be negative.
Therefore, x = 6 gives the speed of the stream
= 6km/h

OR

(B) Two water taps together can fill a tank in 9\(\frac{3}{8}\) hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Solution:
Let the time taken by the smaller pipe to fill the tank = x h
Time taken by the larger pipe = (x – 10) h
Part of the tank filled by smaller pipe in 1 hour = \(\frac{1}{x}\)
Part of the tank filled by larger pipe in 1 hour = \(\frac{1}{x-10}\)
The tank can be filled in 9\(\frac{3}{8}\) = \(\frac{75}{8}\) hours by both the pipes together.
Part of the tank filled by both the pipes in 1 hour = \(\frac{8}{75}\)
Therefore, \(\frac{1}{x}\) + \(\frac{1}{x-10}\) =  \(\frac{8}{75}\)
8x ² – 230x + 750 = 0
x = 25,  \(\frac{30}{8}\)
Time taken by the smaller pipe cannot be \(\frac{30}{8}\) = 3.75 hours, as the time taken by the larger pipe will become negative, which is logically not possible. Therefore, the time taken individually by the smaller pipe and the larger pipe will be 25 and 25 – 10 = 15 hours, respectively.

Question 33.
Draw the graphs of 2x + y = 6 and 2x – y + 2 = 0. Shade the region bounded by these lines and X-axis. Find the area of the shaded region.
Or
Places P ₁ and P ₂ are 250 km apart from each other on a national highway. A car starts from P ₁ and another from P ₂ at the same time. If they go in the same direction, then they meet in 5 h and if they go in opposite directions they meet in \(\frac{25}{13}\) h, then find their speeds. [5]
Solution:
We have, 2x+ y = 6 and 2x – y + 2 = 0
Table for equation y = 6 – 2x is

x	0	3
y	6	0

On plotting the points A(0, 6) and B(3, 0) on a graph paper and join them, we obtain the graph of line represented by the equation 2x + y = 6 as shown in the figure.

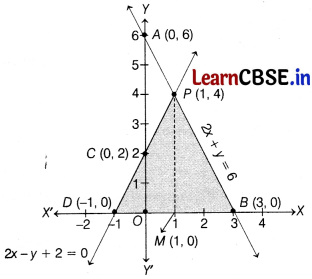
On plotting the pointsC(0,2)and D(-1, 0)on the same graph paper and join them, we obtain the graph of line represented by the equation 2x – y + 2 = 0 as shown in the figure.
The two lines intersect at point P( 1, 4).
Thus, x = 1 and y = 4 is the solution of the given system of equations. The area enclosed by the lines and X-axis is shaded part in the figure. Draw PM perpendicular from P on X-axis.
Clearly, we have
PM = y-coordinate of point P(1, 4)
⇒ PM = 4 and DB = 4
Area of the shaded region = Area of A PSD
= \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\)(DB × PM)
= \(\frac{1}{2}\) × 4 × 4
= 8 sq units

Or

Let A and B be the two cars. A starts from P ₁ with constant speed of x km/h and B starts from P ₂ with constant speed of y km/h.
Case I When the two cars move in same directions as shown in figure, the cars meet at the position Q.

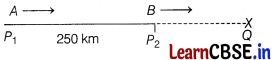
Here, P ₁ Q = 5x km, i.e. the distance travelled by car A in 5 h with x km/h speed.
P ₂ Q = 5y km, i.e. the distance travelled by car B in 5 h with y km/h speed.
We have, P ₁ Q – P ₂ Q = 250
5x – 5y = 250
⇒ x – y = 50 …(i)
Case II When two cars move in opposite directions as shown in figure, the cars meet at the position R.

Here, P ₁ R = \(\frac{25}{13}\) x km and P ₂ R = \(\frac{25}{13}\) y km
So, P ₁ R + P ₂ R = 250
\(\frac{25}{13}\) x + \(\frac{25}{13}\) y = 250
⇒ x + y = 130 ………(ii)
On adding Eq. (i) and Eq. (ii), we get 2x = 180
⇒ 2x = 180
⇒ x = 90
On subtracting Eqs. (i) from (ii), we get
⇒ 2y = 80
⇒ y = 40
∴ Their speeds are 90 km/h and 40 km/h.

Question 34.
(A) Water is flowing at the rate of 15 km/h through a pipe of diameter 14 cm into a cuboidal pond which is 50 m long and 44 m wide. In what time will the level of water in pond rise by 21 cm?
What should be the speed of water if the rise in water level is to be attained in 1 hour?
Solution:
Length of the pond, l = 50 m, width of the pond, b = 44m
Water level is to rise by, h = 21 cm = \(\frac{21}{100}\) m
Volume of water in the pond = lbh
= 50 × 44 × \(\frac{21}{100}\) m ³
= 462 m ³
Diameter of the pipe = 14 cm
Radius of the pipe, r = 7 cm = \(\frac{7}{100}\) m
Area of cross-section of pipe = πr ²

Speed of water if the rise in water level is to be attained in 1 hour = 30 km/h.

OR

(B) A tent is in the shape of a cylinder surmounted by a conical top. If the height and radius of the cylindrical part are 3 m and 14 m respectively, and the total height of the tent is 13.5 m, find the area of the canvas required for making the tent, keeping a provision of 26 m ² of canvas for stitching and wastage. Also, find the cost of the canvas to be purchased at the rate of ₹ 500 per m ² .
Solution:
Radius of the cylindrical tent (r) = 14 m
Total height of the tent = 13.5 m
Height of the cylinder = 3 m
Height of the Conical part = 10.5 m

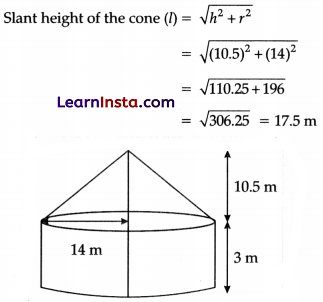
Curved surface area of cylindrical portion = 2πrh
= 2 × \(\frac{22}{7}\) × 14 × 3
= 264 m ²
Curved surface area Of conical portion = πrl
= \(\frac{22}{7}\) × 14 × 17.5
= 770 m ²
Total curved surface area = 264 m ² + 770 m ²
= 1034 m ²
Provision for stitching and wastage = 26 m ²
Area of canvas to be purchased = 1060 m ²
Cost of canvas = Rate × Surface area
= 500 × 1060
= ₹ 5,30,000

Question 35.
Find the unknown entries a, b, c, d, e and f in the following distribution of heights of students in a class

Height (in cm)	Frequency	Cumulative frequency
150-155	12	a
155-160	b	25
160-165	10	c
165-170	d	43
170-175	e	48
175-180	2	f
Total	50

Or
Find the median for the following frequency distribution

Class	0-8	8-16	16-24	24-32	32-40	40-48
Frequency	8	10	16	24	15	7

Solution:
The cumulative frequency table for the given continuous distribution is given below

Height (in cm)	Frequency (f)	Cumulative frequency (given)	Cumulative frequency (cf)
150-155	12	a	12
155-160	b	25	12 + 5
160-165	10	c	22 + 5
165-170	d	43	22 +b + d
170-175	e	48	22 + 5 + d + e
175-180	2	f	24 + b + d + e
Total	50

On comparing last two tables, we get
a = 12
12 + b = 25
⇒ b = 25 – 12 = 13
22 + b = c
⇒ c = 22 + 13 = 35
22 + b + d =43
⇒ 22 + 13 + d = 43
⇒ d = 43 – 35 = 8
22 + b + d + e = 48
⇒ 22 + 13 + 8 + e = 48
⇒ e = 48 – 43 = 5
and 24 + b + d + e = f
⇒ 24 + 13 + 8 + 5 = f
f = 50

Or

We prepare the cumulative frequency table, as given below.

Section E
(Case study based questions are compulsory)

Question 36.

Manpreet Kaur is the national record holder for women in the shot-put discipline. Her throw of 18.86 m at the Asian Grand Prix in 2017 is the maximum distance for an Indian female athlete.

Keeping her as a role model, Sanjitha is determined to earn gold in Olympics one day. Initially her throw reached 7.56 m only. Being an athlete in school, she regularly practiced both in the mornings and in the evenings and was able to improve the distance by 9 cm every week.

During the special camp for 15 days, she started with 40 throws and every day kept increasing the number of throws by 12 to achieve this remarkable progress.
(i) How many throws Sanjitha practiced on 11th day of the camp?
Solution:
Number of throws during camp, a = 40; d = 12
t ₁₁ = a + 10d
= 40 + 10 × 12
= 160 throws

(ii) What would be Sanjitha’s throw distance at the end of 6 weeks?
Solution:
a = 7.56 m; d = 9 cm = 0.09 m
n = 6 weeks
t _n = a + (n – 1)d
t ₁₁ = 7.56 + 6(0.09)
= 7.56 + 0.54
Sanjitha’s throw distance at the end of 6 weeks = 8.1 m

OR

When will she be able to achieve a throw of 11.16 m?
Solution:
a = 7.56 m; d = 9 cm = 0.09 m
t _n = 11.16 m
t _n = a + (n – 1)d
11.16 = 7.56 + (n – 1) (0.09)
3.6 = (n – 1) (0.09)
n – 1 = \(\frac{3.6}{0.09}\) = 40
n = 41
Sanjitha’s will be able to throw 11.16 m in 41 weeks.

(iii) How many throws did she do during the entire camp of 15 days?
Solution:
a = 40; d = 12; n = 15
S _n = \(\frac{n}{2}\) [2a + (n – 1)d]
S _n = \(\frac{15}{2}\) [2(40) + (15 – 1)(12)]
= \(\frac{15}{2}\) [80 + 168]
= \(\frac{15}{2}\) [248]
= 1860 throws

Question 37.
Cylindrical Wooden Article
A wooden article was made by scooping out a hemisphere from one end of a cylinder and a cone from the other end as shown in the figure. If the height of the cylinder is 40 cm, the radius of the cylinder is 7 cm and the height of the cone is 24 cm.

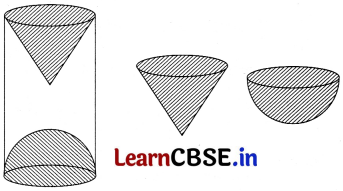
Based on the above information, answer the following questions.
(i) Find the slant height of the cone and volume of the hemisphere. [2]
Or
Find the total volume of the article. [2]
(ii) Find the curve surface area of the cone. [1]
(iii) Find the surface area of the article. [1]
Solution:
Given, the height of the cylinder (H) = 40 cm
The radius of the cylinder (r) = 7 cm
The radius of the hemisphere (r) = 7 cm
The radius of the cone (r) = 7 cm
Height of the cone (h) = 24 cm

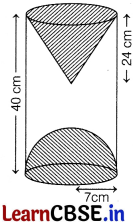
(i) Slant height of the cone (l) = \(\sqrt{h^2 + r^2}\)
= \(\sqrt{(24)^2 + (7)^2}\)
= \(\sqrt{576 + 49}\)
= \(\sqrt{625}\)
= 25 cm
volume of a hemisphere = \(\frac{2}{3}\)πr ³
= \(\frac{2}{3}\) × \(\frac{22}{7}\) × (7) ³
= \(\frac{44}{3}\) × 49
= \(\frac{2156}{3}\) = 718.67 cm³

Or

Volume of the article
= Volume of the cylinder – Volume of the cone – Volume of the hemisphere

(ii) Curve surface area of cone = πrl
= \(\frac{22}{7}\) × 7 × 25 = 22 × 25 = 550 cm²

(iii) Total surface area of the article
= Curved surface area of the cylinder
+ Curved surface area of the cone
+ Surface area of the hemisphere
= 2πrH + πrl + 2πr² = πr [2H + l + 2r]
= \(\frac{22}{7}\) × 7 × [2 × 40 + 25 + 2 × 7]
= 22 × [80 + 25 + 14] = 22 × 119 = 2618 cm²

Question 38.

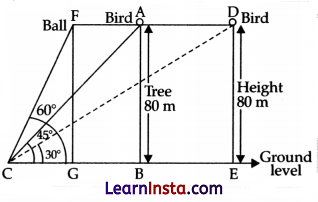
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80 m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°

(i) At what distance from the foot of the tree was he observing the bird sitting on the tree?
Solution:
tan 45° = \(\frac{80}{CB}\)
CB = 80 m

(ii) How far did the bird fly in the mentioned time?
OR
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball?
Solution:

(iii) What is the speed of the bird in m/min if it had flown 20(√3 +1) m?
Solution: