Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 6 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths BasicTerm 2 Set 2 for Practice
Time allowed: 2 hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one questions.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one questions. It contains two case study based questions.
Section – A (12 Marks)
Question 1.
Draw a line segment of length 7.8 cm and divide it in the ratio of 5 : 8.
OR
To draw a pair of tangents to a circle which are inclined to each other at an angle of 60°, it is required to draw tangents at one end points of those two radii of the circle. Then, what should be the angle between the radii?
(2)
Question 2.
If the equation x
2
+ kx + 12 = 0 has 2 as one of its root and the equation x
2
+ kx + q = 0 has equal roots, then what is the value of q? (2)
Question 3.
The following are the ages of 800 patients getting medical treatment in a hospital on a particular day.
| Age (in years) | No. of Students |
| 10-20 | 60 |
| 20-30 | 42 |
| 30-40 | 55 |
| 40-50 | 70 |
| 50 – 60 | 53 |
| 60 – 70 | 20 |
Form the less than type cumulative frequency distribution table.
Question 4.
In an AP, if a = 7, a
13
= 35, find d and S
13
. (2)
Question 5.
There are 2 circles of centres P and Q of radii 9 cm and 2 cm respectively. PQ the line joining the centers is 17 cm. Another circle with centre R have radius 2 cm, which touches the other two circles externally. Write an equation in terms of x, if ∠PRQ = 90°. (2)
Question 6.
A solid cube is cut into 2 cuboids of equal volumes. What is the ratio of the total surface area of the given cube to that one of the cuboid?
OR
Circumference of the edge of a hemispherical bowl is 132 cm. What is the capacity of the bowl? Use π = \(\frac{22}{7}\) (2)
Section – B (12 marks)
Question 7.
In a health check up camp of women in the age of 40+ years, the number of heart beats of women were recorded in the following table.
Number of heart beats/ minute Number of women
| Number of heart beats/ minute | Number of women |
| 65-69 | 2 |
| 70-74 | 18 |
| 75-79 | 16 |
| 80-84 | 4 |
Find the mean of the data. (3)
Question 8.
Rohan is flying a kite. Being a student, he tried to estimate the length of the string he is using to fly that kite. The kite is flying at height of 90 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Then find the length of the string assuming there is no slack in the string. (3)
Question 9.
Two tangents segments BC, BD are drawn to a circle with centre O, such that ∠DBC = 120°. Prove that BO = 2BC. (3)
Question 10.
What is the median of the first ten prime numbers?
OR
60 accidents reported were randomly picked up from local evening newspaper involving the age of drivers.
| Age group | No. of Students |
| 0-20 | 17 |
| 20-40 | 12 |
| 40-60 | 24 |
| 60-80 | 12 |
| 80-100 | 5 |
Find the mode of the data (3)
Section – C (16 marks)
Question 11.
A rectangular tank is 225 m and 162 m at base. With what speed should water flow into it through an aperture 60 cm × 45 cm, so that the level of water is raised by 20 cm in 2.5 hours ? (4)
Question 12.
The angle of elevation from the top of a building from the foot of a tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
OR
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower. (4)
Question 13.
Case Study—1
Time is of the essence in human life. Time and tide waits for none, which means that just like tide even time does not wait for anyone. Shweta was very particular in her work and fond of buying new-new watches and clock. She went to a gift shop in which she saw a beautiful clock.
This table clock reminded Shweta of a particular shape in which a circle is inscribed inside a triangle And sides of a triangle are touching the circle as the tangents to the circle.
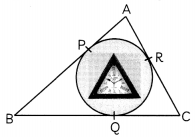
In the given figure, PA = 4 cm, BP = 3 cm and AC = 11 cm.
Now, answer the following question:
(A) In the given figure, calculate the length of side RC. (2)
(B) If O is the centre of the circle and length of OB is 5 cm, then what is the radius of the circle? (2)
Question 14.
Case Study—2
Akshay is a fitness freak and great athlete. He always want to make his nation proud by winning medals and prizes in the athletic activities.
An upcoming activity for athletes was going to be organised by Railways. Akshay want to participate in 200 m race. He can currently run that distance in 51 seconds. But he wants to increase his speed, so to do it in 31 seconds. With each day of practice it takes him 2 seconds less.

(A) He wants to makes his best time as 31 sec. in how many days will be able to achieve his target? (2)
(B) What will be the difference between the time taken on 5th day and 7th day. (2 )