Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 3 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths BasicTerm 2 Set 3 with Solutions
Time allowed: 2 hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one questions.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one questions. It contains two case study based questions.
Section – A (12 marks)
Question 1.
By mistake, the coefficient of x in quadratic equation x
2
+ ax + b = 0 was taken as 17 in place of 13; whose roots were found to be – 2 and – 15. What are the roots of the original equation?
OR
In the equation (c
2
– ab) x
2
– 2(a
2
– bc)x + b
2
– ac = 0, if the roots are equal, then show that either q = 0 or a
3
+ b
3
+ c
3
= 3abc. (2)
Answer:
When coefficient of x is 17. roots of the equation are -2 and -15.
i.e x
2
+ 17x + b = 0
⇒ (-2)
2
+ 17(–2) + b = 0
⇒ b = 30
Now, original equation becomes
x
2
+ 13x + 30 = 0
x
2
+ 10x + 3x + 30 = 0
⇒ x(x + 10) + 3(x + 10) = 0
⇒ x = -10,-3
Hence, original roots are – 3 and – 10.
OR
The given equation is;
(c
2
– ab)x
2
– 2(a
2
– bc)x + b
2
– ac = 0
Since, roots ore equal
∴ D = 0
or B
2
– 4AC = 0
∴ 4(a
2
– bc)
2
– 4(c
2
– ab) (b2 -ac) = 0
⇒ 4[a
4
+ b
2
c
2
– 2a
2
bc – b
2
c
2
+ ac + ab
3
– a
2
bc] = 0
⇒ a
4
– 3a
2
bc + ac
3
+ ab
3
= 0
⇒ a(a
3
+ b
3
+ c
3
– 3abc) = 0
Either a = 0 or a
3
+ b
3
+ c
3
= 3abc.
Question 2.
If in an A.P., the sum of first p terms is ap
2
+ bp, then what is its common difference. (2)
Answer:
Here, S
p
= ap
2
+ bp
Then S
p-1
=a(p – 1)
2
+ b(p – 1)
∴ a
p
= S
p
— S
p-1
= (ap
2
+ bp) -[a(p – 1)
2
+ b(p- 1)]
= ap
2
+ bp – (ap
2
+ a – 2ap + bp – b)
= ap
2
+ bp – ap
2
– a + 2ap – bp + b)
= ap
2
+ bp – ap
2
– a + 2ap – bp + b
= 2ap + b – a
a
1
= 2a + b – a, (p = 1)
= a + b
a
2
= 4a + b – a
= 3 a + b
d = a
2
– a
1
= (3o + b) – (a + b)
= 2a
Question 3.
The mean of the following data is 12, then what is the value of p? (2)
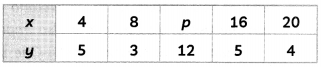
Answer:
Here, the given data is
| x | f | fx |
| 4 | 5 | 20 |
| 8 | 3 | 24 |
| P | 12 | 12p |
| 16 | 5 | 80 |
| 20 | 4 | 80 |
| Σf = 29 | Σfx = 204 + 12p |
But, mean = 12
x̄ = \(\)
12 = \(\)
12p = 348 – 204
p = \(\frac{144}{12}\) = 12
Caution
Draw the appropriate table, and use the required formula for finding the value
Question 4.
A student taking a test consisting of 10 questions is told that each question after the first question is worth 2 marks more then the preceeding questions. If third question of the test is worth 5 marks, what is the maximum score that the student can obtain by attempting 8 questions? (2)
Answer:
Here, difference between 2 questions is of 2 marks.
∴ d = 2
Numbers of questions
n = 10
And a= 5
∴a + (n – 1)d = 5
⇒ a + (3 – 1) × 2 = 5
⇒ a = 5 – 4 = 1
If n = 8, then maximum marks obtained when starting question 3 is.
S
8
= \(\frac{n}{2}\)[2a + (n – 1)d]
= \(\frac{8}{2}\) [2 × 5 + (8 – 1) × 2]
= 4(10 + 14)
= 4 × 24
= 96
Hence, 96 is the maximum marks obtained by the student.
Caution
Here, maximum marks will be obtained by solving the question of the maximum mark i.e. questions in the last.
Question 5.
Find the value x and y from the given cumulative distribution. (2)
| Classes | Frequency | c.f |
| 0-8 | 15 | 15 |
| 8-16 | x | 28 |
| 16-24 | 15 | 43 |
| 24-32 | 18 | y |
| 32-40 | 09 | 70 |
Answer:
From the cumulative frequency distribution:
15 + x = 28
⇒ x= 28-15 = 13
and 43 + 18 = y
⇒ y = 61
Hence, value of x is 13 and y is 61.
Question 6.
A toy is in the shape of a hemisphere surmounted by a cone, as shown in the figure
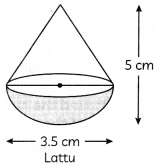
What is the surface area of the complete toy ?
OR
The figure shows a wax candle in the shape of right circular cone with base radius 5 cm and height 12 cm. It takes 1 hour 40 minutes to burn completely
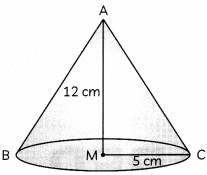
What is volume of the candle before it started burning? (2)
Answer:
Area of toy = C.S.A of cone + C.S.A. of hemisphere
= πrl + 2πr
2
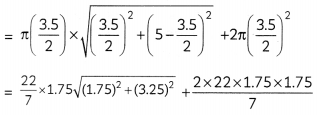
= 20.30 + 19.25
= 39.55
≅ 40 sq. cm
OR
Here, shape of the candle is a cone, whose height,
h = 12 cm and radius,
r = 5 cm
∴ Volume of the candle = πr
2
h
= π × 5 × 5 × 12 = 300 π cm
2
Caution
Candle when not burnt, will be in the shape of a cone.
Section – B (12 marks)
Question 7.
If PA and PB are any two tangents drawn from a point P to a circle with centre O, touching it at A and B, then prove that OP is the perpendicular bisector of AB. (3)
Answer:
Let OP intersect AB at a point C. Here, PA and PB are the two tangents from a point P lying outside the circle, to the circle with centre O.
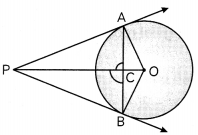
∠APO = ∠BPO
[∵ O Lies on the bisector of ∠APB]
Now, in ∆ACP and ∆BCP, we have
AP = BP (tangents from an external point)
PC = PC (Common)
∠APO = ∠BPO (Proved above)
⇒ ∆ACP ≅ ∆BCP [By SAS congruence axiom]
⇒ AC = BC [by c.p.ct]
And ∠ACP = ∠BCP
⇒ \(\frac{1}{2}\) × 180 = 90° [by c.p.ct]
Hence OP is the perpendicular bisector of AB.
Question 8.
A man is standing on the deck of a ship, which is 10 m above water level and observes the angle of elevation of the top of a hill as 60° and angle of depression of the base as 30°. Find the distance of the hill from the ship and height of the hill.
OR
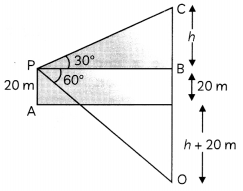
At a point P, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30°. The angle of depression of the cloud in the lake, at P is 60°. Find the distance of the cloud from P? (3)
Answer:
Here, PQ is the deck of the ship and man is standing at the point P. AC is a hill and from point P, the angle of elevation is 60° and angle of depression is 30°
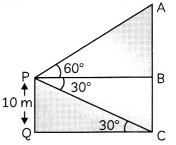
∴ In ∆PQC,
tan 30° = \(\frac{\mathrm{PQ}}{\mathrm{QC}}\)
\(\frac{1}{\sqrt{3}}=\frac{10}{Q C}\)
⇒ QC = 10√3 m
Now, QC = PB = 10√3 m
Now, in ∆ABP
tan 60° = \(\frac{AB}{PB}\)
√3 = \(\frac{\mathrm{AB}}{10 \sqrt{3}}\)
AB = 30 m
∴ Distance of hill from ship = 10√3 m
and height of the hill = AB + BC
= 30 + 10
= 40 m
Related Theory
Angie of elevation denotes the angle from the horizontal upward to an object. And angle of depression denotes the angle from the horizontal downward to an object.
OR
Let BP be x m
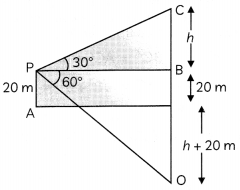
In ∆BPC
tan 30° = \(\frac{\mathrm{BC}}{\mathrm{BP}}\)
\(\frac{1}{\sqrt{3}}=\frac{h}{x}\)
⇒ x = √3h ………..(i)
From ∆PBO
tan 60° = \(\frac{\mathrm{BO}}{\mathrm{PB}}\)
⇒ √3 = \(\frac{20+20+h}{x}\)
x = \(\frac{40+h}{\sqrt{3}}\) ……….(ii)
From (i) and (ii)
\(\frac{40+h}{\sqrt{3}}\) = √3h
⇒ 3h = 40 + h
⇒ 2h = 40
h = 20 m
x = \(\frac{40+20}{\sqrt{3}}\)
= \(\frac{60}{\sqrt{3}}\)
= 20√3
PC = \(\sqrt{B C^{2}+P B^{2}}\)
= \(\sqrt{20^{2}+(20 \sqrt{3})^{2}}\)
= \(\sqrt{400+1200}\)
= \(\sqrt{1600}\)
= 40 m
Caution
Here, final answer that is to be calculated is the distance between cloud and the observer not the height of the cloud from the lake.
Question 9.
In the figure, ABC is a right-angled triangle with AB = 6 cm and AC = 8 cm. A circle with centre O has been inscribed inside the triangle. Calculate the value of r, the radius of the inscribed circle. (3)
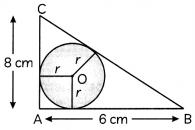
Answer:
In ∆ABC, BC
2
= AC
2
+ BA
2
BC = \(\sqrt{8^{2}+6^{2}}=\sqrt{100}\) = 10 cm
Join OA, OB and OC
Now, area of (∆OAC + ∆OAB + ∆BOC) = Area of ∆ABC
⇒ \(\frac{1}{2}\) × 8 × r + \(\frac{1}{2}\) × 6 × r + \(\frac{1}{2}\) × 0 × r = \(\frac{1}{2}\)
⇒ 4r + 3r + 5r = 24
⇒ 12r = 24
⇒ r = 2 cm
Question 10.
Prove that the lengths of tangents drawn from an external point to a circle are equal. (3)
Answer:
Let, AP and AQ be two tangents drawn to the circle from the externaL point A.
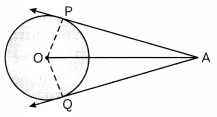
We need to show that AP = AQ
Join OA, OP and OQ
Consider ∆OPA and ∆OQA
Here, OP = OQ (Radius of the circle)
OA = OA (Common)
∠OPA = ∠OQA = 90°
(by property of tangent)
∴ ∆OPA ≅ ∆OQA
∴ PA = QA or AP = AQ
Caution
While proving any statement, give all the necessary steps in the detailed manner, with the reason.
Section – C (16 marks)
Question 11.
From the first floor of Qutub Minor, which is at a height of 25 m from the level ground, a man observes the top of a building at an angle of elevation of 30° and angle of depression of the base of the building to be 60°. Calculate the height of the building.
OR
Two pillars of equal height, stand on either side of a roadway which is 150 m wide. From a point on the roadway between the pillars, the elevations of the top of the pillars are 60° and 30°. Find the height of the pillars and the position of the point at which angle
of elevation is calculated. [Use √3 = 1.732] (4)
Answer:
Let, the first floor of Qutub Minar AB be at the point X.
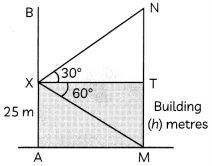
Let MN represent the building.
Here, XT ∥ AM.

Thus, the height of the building MN = MT + TN
= (25 + \(\frac{25}{3}\))
= \(\frac{100}{3}\) m
= 33\(\frac{1}{3}\) m
OR
Let h metres be the height of each pillar and point P be x metres away from pillar AB point
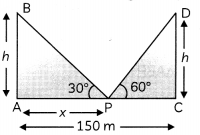
In ∆PCD,
\(\frac{h}{PC}\) = tan 60° = √3
⇒ PC = \(\frac{h}{\sqrt{3}}\) …….(i)
In ∆PAB,
\(\frac{h}{PA}\) = tan 30° = \(\frac{1}{\sqrt{3}}\)
PA = √3h ……..(ii)
Now, PA + PC = 150
√3h + \(\frac{h}{\sqrt{3}}\) = 150
⇒ 3h + h = 150√3
⇒ 4h = 150√3
h = \(\frac{150 \sqrt{3}}{4}\)
= 64.875 m
Also, PA = √3h
= √3 × \(\frac{150}{4}\) × √3
= 112.5 m
Thus, the height of the pillar is 64.875 m and the position of the point is at a distance of 112.5 m from the pillar AB.
Caution
Here, point ¡s in between the two plU ors, not the mid point of AC
Question 12.
If the diameter of cross- section of a wire is decreased by 5%. By how much percent will length be increased, so that the volume remains the same ? (4)
Answer:
If R be the radius and H be the height of the wire.
∴ Original volume = πR
2
H
When diameter is decreased by 5%, then radius is also decrease by 5%
New radius = R – \(\frac{5 R}{100}=\frac{95 R}{100}=\frac{19 R}{20}\)
New Radius = π\(\left(\frac{19 R}{20}\right)^{2}\)H
= \(\frac{\pi H \times 361 R^{2}}{400}\)
But we have to maintain the volume at the constant level, so length H is to be multiplied by \(\frac{400}{361}\) to keep it constant.
So, new length = \(\frac{400H}{361}\)
% Increase in Length = \(\frac{\frac{400 \mathrm{H}}{361}-\mathrm{H} \times 100}{361 \mathrm{H}}\)
= \(\frac{39}{361}\) × 100
= 10.8%
Question 13.
Case Study—1
Arithmetic progression has a wider application in day-to-day Life It can be applied in real life by analysing a certain pattern. For example, AP is used in straight Line depreciation, etc. The arithmetic sequence is important in real life because this enables us to understand things with the use of patterns. It is also important in stimulating systematic events. One use of arithmetic progression is in tissue paper roll, in which the first term is the diameter of the core of the roll and twice the thickness of the paper is the common difference. If sum of first n rolls of tissue and on a roll is S
n
= 0.1n
2
+ 7.9 n then answer the following questions.

(A) What is the nth term in the given sequence? (2)
(B) What is the common difference of the progression formed by tissue rolls? (2)
Answer:
Case Study—1
(A) Here.
S
n
= 0.1n
2
+ 7.9 n
Then a
n
= S
n
– S
n-1
= O.1n
2
+ 7.9n – [0.1 (n – 1)
2
+ 79(n – 1)]
= O.1n
2
+ 7.9n – [0.1(n
2
+ 1 – 2n) + 79n – 7.9]
= O.1n
2
+ 7.9n – [0.1n
2
+ 0.1 – 0.2n + 7.9n + 7.9]
= 7.9n – 0.1 + 0.2n – 7.9n + 7.9
= 7.8n + 0.2n
(B) S
1
= a
1
= 0.1(1)
2
+ 7.9(1)…(i)
= 8
a
2
= S
2
– S
1
= 0.1(2)
2
+ 7.9(2) – 8
= 0.4 + 15.8 – 8
= 16.2 – 8
= 8.2
Then, d = a
2
– a
1
= 8.2 – 8 = 0.2
Question 14.
Case Study—2
National Highway Authority of India (NHAI) has installed toll tax plaza or collection centre on highway for the maintenance of roads and highways. NHAI had set up booths to collect the toll taxes. They collect the toll tax only from the four wheeler or larger vehicle drivers who pass by toll roads. The central government levy fees at such rates as may be laid down by rules made in this behalf for services or benefits rendered in relation to the use to ferries, permanent bridges and tunnels on national highways and the use of sections of national highways.

On a particular day, NHAI checked the toll tax collection of a particular toll plaza in Mathura Uttar Pradesh.
The table shows the toll tax paid by drivers and the number of vehicles on that particular day:
| Toll tax (in ₹) | No. of vehicles |
| 30-40 | 90 |
| 40 – 50 | 100 |
| 50-60 | 110 |
| 60-70 | 80 |
| 70-80 | 40 |
(A) What is the mean value of the toll tax received by NHAI on a particular day from a particular toll plaza? (2)
(B) What is the median value of the given data? (2)
Answer:
| Toll tax (in ₹) | f i | x i | f i x i |
| 30-40 | 90 | 35 | 3150 |
| 40-50 | 100 | 45 | 4500 |
| 50-60 | 110 | 55 | 6050 |
| 60-70 | 80 | 65 | 5200 |
| 70-80 | 40 | 75 | 3000 |
| 420 | 21,900 |
∴ Mean = \(\frac{\Sigma f_{i} x_{i}}{\Sigma f_{i}}\)
= \(\frac{21900}{420}\)
= 52.14 (approx)
(B)
| CI | f | cf |
| 30-40 | 90 | 90 |
| 40-50 | 100 | 190 |
| 50-60 | 110 | 300 |
| 60-70 | 80 | 380 |
| 70-80 | 40 | 420 |
| 420 |
Now, \(\frac{N}{2}=\frac{420}{2}\)
= 210
Median doss = 50 – 60
Then median = l + \(\frac{\frac{N}{2}-c f}{f}\) × h
= 50 + \(\frac{210-190}{110}\) × 10
= 50 + \(\frac{200}{110}\)
= 50 + 1.81
= 51.81