Students can access the CBSE Sample Papers for Class 10 Maths with Solutions and marking scheme Term 2 Set 2 will help students in understanding the difficulty level of the exam.
CBSE Sample Papers for Class 10 Maths BasicTerm 2 Set 2 with Solutions
Time allowed: 2 hours
Maximum Marks: 40
General Instructions:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one questions.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one questions. It contains two case study based questions.
Section – A (12 marks)
Question 1.
Write the equation x = \(x=\sqrt{6+\sqrt{6+\sqrt{6}}}\)…. in the form of a quadratic equation, where, x is a natural number.
OR
State whether the equation (x + 1) (x – 2) + x = 0 has two distinct real roots or not. Justify your answer. (2)
Answer:
We have:
x = \(\sqrt{6+\sqrt{6+\sqrt{6}}}\)……
On squaring both sides, we get
x
2
= \(6+\sqrt{6+\sqrt{6+\sqrt{6}}}+\)…….
⇒ x
2
– x – 6 = 0,
which is the required quadratic equation.
Concept Applied:
In algebra a quadratic equation is any equation that can be rearranged in standard form as ax2 + b + c = 0 where x represents an unknown variable, a, b and c represent known numbers where a ≠ 0, If a = 0, then equation is linear, not quadratic.
OR
(x + 1) (x – 2) + x = 0
⇒ x
2
– x – 2 + x=0
⇒ x
2
– 2 = 0
We get, a = 1, b = 0 c = 2
∵ D = b
2
– 4ac
∴ 0 – 4 × 1 × (- 2) = 8 > 0
Hence, given equation has two district real roots.
Caution:
W Convert the equation in the form ax
2
+ bx + c = 0, to get the discriminant of the quadratic equation.
Question 2.
To make the walls of the room beautiful wallpaper is required. The wallpaper is 312 cm long and 25 cm wide. Length of the room is 7 m and its breadth is twice its height. Calculate the height of the room. (2)
Answer:
Area of wallpaper = 312 × 0.25
= 78.00 m
2
Length of room = 7 m
Let, height of room be x m, then breadth is 2x
∴ Area of four walls = 2(l × h + b × h)
A.T.Q 4×2 + 14x = 78
⇒ 2x
2
+ 7x – 39 = 0
⇒ 2x
2
+ 13x – 6x – 39 = 0
⇒ x(2x + 13) – 3(2x + 13) = 0
⇒ x = 3 or x = \(\frac{-13}{2}\) (rejected)
Hence, height of room is 3 m.
Caution:
Use the splitting of middle term method to get the value of x, in the quadratic equation formed in the condition.
Question 3.
Determine the median class for the following distribution (2)
| Class | Frequency |
| 0 – 10 | 5 |
| 10 – 20 | 3 |
| 20 – 30 | 4 |
| 30 – 40 | 3 |
| 40 – 50 | 6 |
| 50 – 60 | 12 |
Answer:
| Class | Frequency | C.F. |
| 0-10 | 5 | 5 |
| 10-20 | 3 | 8 |
| 20 – 30 | 4 | 12 |
| 30 – 40 | 3 | 15 |
| 40 – 50 | 6 | 21 |
| 50 – 60 | 12 | 33 |
| N = 33 |
Here N = 33,
\(\frac{N}{2}\) = \(\frac{33}{2}\)
= 16.5
Since, \(\frac{N}{2}\) = 16.5 Then, median class is 40 – 50
caution:
Median cLass is the dass having the cumulative frequency just greater than \(\frac{N}{2}\)
Question 4.
If the sum of four numbers in A.P. are such that their sum is 50 and greatest number is 4 times the least, then evaluate the numbers. (2)
Answer:
Consider the numbers as a, a + d, a + 2d, a + 3d
A.T.Q., a + a + d+ a + 2d + a + 3d = 50
⇒ 4a + 6d = 50
⇒ 2a + 3d = 25 ……….. (i)
and
a + 3d = 4a
3d = 3a
⇒ a = d ……. (ii)
From equations (i) and (ii), we get
a = d = 5
Numbers are 5, 10, 15, 20
Question 5.
Determine the mode of the following data (2)
| Class | Frequency |
| 0-20 | 15 |
| 20-40 | 6 |
| 40-60 | 18 |
| 60-80 | 10 |
Answer:
Here, the class with maximum frequency is 40-60
∴ Mode = l + \(\frac{f_{1}-f_{0}}{2 f_{1} f_{0}-f_{2}}\) × h
= 40 + \(\frac{18-6}{36-6-10}\) × 20
= 40 + \(\frac{12 \times 20}{20}\) = 52
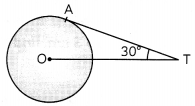
Question 6.
In the figure, AT is a tangent to the circle with centre O, such that OT = 8 cm and ∠OTA = 30°. What is the length of AT?
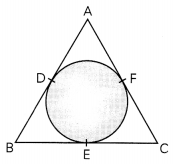
In the figure, if AB = AC, then prove that BE = EC. (2)
Answer:
Here, AT is the tangent to the circle with centre O.
∴ ∠OAT = 90° (By property of tangent)
In ∆OAT,
cos 30° = \(\frac{\mathrm{AT}}{\mathrm{OT}}\)
⇒ \(\frac{\sqrt{3}}{2}\) = \(\frac{\mathrm{AT}}{8}\)
⇒ AT = 4√3 cm
Caution:
Use the property of tangent and trigonometric ratios to get the answer.
OR
Given: AB = AC
To Prove: BE = EC
Since, length of tangent from an external point are equal.
∴ AD = AF …….. (i)
BE = BD …….. (ii)
EC = CF ……. (iii)
But, AB = AC
AD + BD = AC = AF + FC (Given)
⇒ AF + BD = AF + FC [from (i)]
⇒ BD = CF
⇒ EC = CF [From (ii) and (iii)] Hence, proved.
Section – B (12 marks)
Question 7.
The sum of n terms of an A.P., whose first term is 6 and common difference is 40 is equal to the sum of 2n terms of another A.P., whose first term is 40 and common difference is 6. Find n. (3)
Answer:
For 1
st
A.P.
First term, a = 6,
Common difference, d= 40
Sum of n terms = \(\frac{n}{2}\)[2 × 6 + (n – 1) × 40]
= \(\frac{n}{2}\) [12 + 40n – 40]
= \(\frac{n}{2}\) [40n – 28]
For II
nd
A.P.
First term A = 40.
Common difference, d = 6
Sum of 2n terms
= \(\frac{2n}{2}\) [2 × 40 + (2n – 1)6]
= n[80 + 12n – 6]
= n[74 + 12n]
A.T.Q.,
\(\frac{n}{2}\)(40n – 28) = n(74 + 12n)
⇒ 40n – 28 = 148 + 24n
⇒ 16n = 176
n = 11
Question 8.
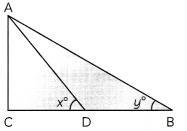
In the given figure, a bird is flying at the point A and two persons are standing at the point B and D, such that D is the mid-point of BC and observing the bird. Then, find the value of \(\frac{\tan x^{\circ}}{\tan y^{\circ}}\).
OR
In an experiment, some masses are hung in equilibrium as shown in the figure. AB = 40 cm, ∠CAB = 45° and ∠CBA = 30°.
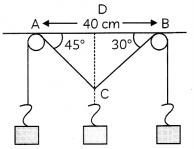
Find
(A) the perpendicular distance of AB from C.
(B) the length of AC
(C) the length of BC (3)
Answer:
Here, D is the mid-point of BC
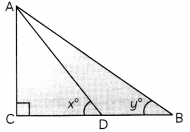
∴ BD = CD
In ∆ACD
tan x° = \(\frac{A C}{C D}\)
In ∆ACB
tan x° = \(\frac{A C}{B C}\)
= \(\frac{A C}{2 C D}\) (∵ BD = CD)
∴ \(\frac{\tan x^{\circ}}{\tan y^{\circ}}\) = \(\frac{A C / C D}{A C / 2 C D}\)
= \(\frac{2 C D}{C D}\)
= 2 : 1
Related Theory:
Value of tangent of an angle depends on the dimensions of perpendicular and base.
OR
(i) Draw CD ⊥ AB

In right angled ∆ADC
\(\frac{A D}{C D}\) = cot 45°
⇒ AD = CD
In right ABDC
\(\frac{B D}{C D}\) = cot 30° = √3 CD …… (i)
⇒ BD = √3 CD ………… (ii)
Adding (i) and (ii), we get
40 = AD + BD
40 = CD + √3CD
40 = 2.732
CD = \(\frac{40}{2.732}\)
= 14.64 cm
≈ 14.6 cm
(i) In right ∆ADC
\(\frac{C D}{A C}\) = sin 45°
⇒ AC = √2CD
= 0.414 × 14.64
= 20.7 cm
(iii) In right ∆BDC
\(\frac{C D}{B C}\) = sin 30°
⇒ BC = 2 × CD,
= 2 × 14.64 = 23.28
≈ 29.3 cm
Caution:
Here, drawing of line CD is important to calculate the value of the required sides as by drawing it, the right-angled triangles are obtained which are used to calculate the required sides by using trigonometric ratios.
Question 9.
In the given figure, calculate the perimeter of ∆PCD (3)
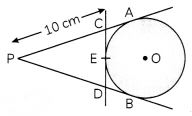
Answer:
Here, PA = 10 cm
Since, tangents from an external point are equal
∴ PA = PB = 10 cm „.(i)
Now, CA and CE are also the tangents from an external point C.
∴ CA = CE …(ii)
Similarly, DB = DE …(iii)
Perimeter of ∆ PCD = PC + CD + PD
= PC + CE + ED + PD
= PC + CA + DB + PD
[Using (ii) and (iii)]
= DA + PB
= 2PA [Using (i)]
= 2 × 10 = 20 cm
Related Theory:
(A) When a point lies outside the circle, then two tangents can be drawn from that point to the circle.
(B) When a point lies on the circle, then a single tangent can be drawn.
(C) When a point lies inside the circle, then no tangent can be drawn.
Question 10.
If the roots of the quadratic equation p(q – r)x
2
+ q(r – p)x = 0 are equal, then show \(\frac{1}{p}+\frac{1}{r}=\frac{2}{q}\) (3)
Answer:
Given, quadratic equation is:
p(q – r)x
2
+ q(r – p)x + r(p – q)= 0
On comparing the given equation with standard equation:
ax
2
+ bx + c = O
Here, a = p(q – r), b = q (r – q), c = r(p – q)
∴ D = b
2
– 4ac
= [q(r – p)]
2
– 4 x p(q – r) X r(p – q)
= q
2
(r – p)
2
– 4pr(q – r)(p – q)
= q
2
(r
2
+ p
2
– 2pr) – 4pr(pq – pr – q
2
+ qr)
= q
2
r
2
+ q
2
p
2
– 2prq
2
– 4p
2
qr + 4prq
2
+ 4p
2
r
2
– 4pr
2
q
= q
2
r
2
+ q
2
p
2
+ 2prq
2
– 4p
2
qr +4p
2
r
2
– 4pqr
2
∴ D = (2pr – qr – pq)
2
For equal roots. =0
(2pr – qr – qp)
2
=0
⇒ 2pr – qr – qp=0
⇒ qr + qp = 2pr
On dividing both sides by pqr, we get
\(\frac{q r}{p q r}+\frac{q p}{p q r}=\frac{2 p r}{p q r}\)
⇒ \(\frac{1}{p}+\frac{1}{r}=\frac{2}{q}\)
Related Theory:
- When, discriminant D = b 2 – 4ac is (positive) we get two real solutions.
- When D = 0. then we get just one real solution (both answers are the same).
- When it is negative, we get a pair of complex solution.
Section – C (16 marks)
Question 11.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at angle of 80°.
OR
Draw two concentric circles of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also, measure its length. (4)
Answer:
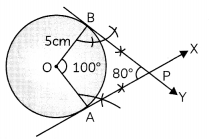
Steps of construction:
(1) Draw a circle with center O and radius 5cm.
(2) Draw any radius OA.
(3) At point O, construct ZAOB = 100°, intersecting the circumference of the circle at B.
(4) At points A and B, construct ZOAX = ZOBY = 90° respectively.
Let ray AX and BY intersect each other at point P.
Then, AP and BP are the required tangents to the circle, which are inclined to each other at an angle of 80°.
OR
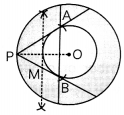
Steps of construction:
(1) Take point O. Draw 2 concentric circles of radii 3 cm and 5 cm respectively.
(2) Mark point P on the circumference of the larger circle.
(3) Join OP and bisect it
(4) Let M be its mid-point
(5) Taking M os a centre and MP as the radius. draw the arc intersecting smaller circle at A and B
(6) Join PAand PB.
Thus, PA and PB are the required tangents
Caution:
Draw the figure, with o pointed pencil, so the lines should not be overlapping and untidy.
Question 12.
The following table given production yield per hectare of wheat of 100 farms of a village
| Production Yields(in kg/ha) | No. of farms |
| 50-55 | 2 |
| 55-60 | 8 |
| 60-65 | 12 |
| 65-70 | 24 |
| 70-75 | 38 |
| 75-80 | 16 |
Change to the distribution a ‘Less than type’ distribution and find its mean. (4)
Answer:
The given data could be converted to less than type distribution.
| Production yields in kg/ ha | No. of farms (f) | c.f. |
| 50-55 | 2 | 2 |
| 55-60 | 8 | 10 |
| 60-65 | 12 | 22 |
| 65-70 | 24 | 46 |
| 70-75 | 38 | 84 |
| 75-80 | 16 | 100 |
| 100 |
Now for mean,
This is the required distribution
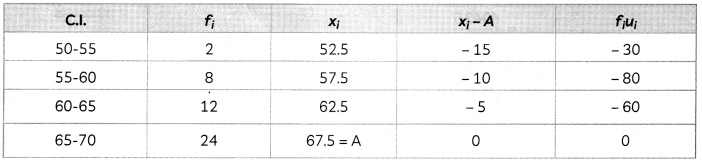

Then, mean = A + \(\frac{\sum f_{i} u_{i}}{\sum f_{i}}\)
= 67.5 + \(\frac{180}{100}\)
= 69.3
Question 13.
Case Study – 1
Sara and Hema, went to enjoy their holidays in a hill station Himachal Pradesh blessed with spectacular and gorgeous mountains and river valleys. Himachal Pradesh is India’s outdoor adventure playground. Both of the girls were thrilled about the fascinating experience of the state. During day time Sara, who is standing on the ground spots a paraglider at a distance of 24 m from him at an elevation of 30°. Her friend, Hema is also standing on the roof of a 6m high balcony, observes the same paraglider at the angle of elevation of 45°. Both of them are on the opposite sides of the paraglider.
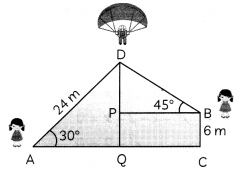
(A) How high is the paraglider flying from the ground? (2)
(B) How far is paraglider from the girl standing on the roof of the building? (2)
Answer:
(A) Here. paragtider is at the points D and he/she is at a distance of DQ from the ground.
In ∆ADQ, sin 30° = \(\frac{\mathrm{DQ}}{\mathrm{AD}}\)
⇒ \(\frac{1}{2}=\frac{\mathrm{DQ}}{24}\)
⇒ DQ = 12cm
Hence, height at which paraglider flying is 12cm.
(B) The girl standing on the roof of the building is Hema.
Here. DQ = 12 m
and PQ = BC = 6cm
∴ DP = DQ – PQ
= 12 – 6 = 6m
∴ In ∆BPD, sin 45° = \(\frac{D P}{B D}\)
⇒ \(\frac{1}{\sqrt{2}}=\frac{6}{B D}\)
⇒ BD = 6√2 m
Hence. distance between paralider and Hema as 6√2m.
Question 14.
Case Study – 2
Every one is very much excited when a New year begins with a new caiendar, Despite it is very cold on that day, but still everybody enjoy having ice-creams as desserts So, to make it fun. On the occasion of New Year, Shweta’s father bought an ice-cream brick. For making it interesting, she bought some ice-cream cones along with it, as children enjoy eating ice-cream in cones.
He bought a 1.51 ice cream brick, whose dimensions are (30 x 25 x 10) cm3. The ice¬cream is filled in the cones in the shape of hemisphere on it, whose radius is 3.5 cm. The height of the cone is 15 cm and radius is 3.5 cm.

(A) If each cone needed to be filled upto brim, then how many scoops are required to fill the cone? (2)
(B) If the complete ice-cream in the brick is distributed in cones, how many cones will be filled by the ice-cream. (2)
Answer:
(A) Volume of a cone = \(\frac{1}{3}\)πr
2
h
= \(\frac{1}{3} \times \frac{22}{7}\) × (3.5)
2
× 15
= \(\frac{4042.5}{21}\)
= 192.5 cm
3
Volume of one scoop = \(\frac{2}{3}\)πr
3
= \(\frac{2}{3} \times \frac{22}{7}\) × 3.5 × 3.5 × 3.5
= \(\frac{1886.5}{21}\) = 89.83 cm
3
∴ Number of scoop required = \(=\frac{\text { Volume of cone }}{\text { Volume of one scoop }}\)
= \(\frac{192.5}{89.83}\) = 2.14 ≈ 2
(B) Volume of ice-cream brick
= l × b × h
= 30 × 25 × 10
= 7500 cm
3
Volume of 1 cone = \(\frac{1}{3}\)πr
2
h
= \(\frac{1}{3} \times \frac{22}{7}\) × 35 × 3.5 × 15
= 192.5 cm
3
∴ Number of cones needed to distribute complete ice-cream
= \(\frac{7500}{192.5}\)
= 38.96
≈ 39 cones
Hence, total ice-cream can be distributed in 39 cones.