CBSE Sample Papers for Class 10 Maths Basic Set 4 with Solutions

Students must start practicing the questions from CBSE Sample Papers for Class 10 Maths Basic with Solutions Set 4 are designed as per the revised syllabus.

CBSE Sample Papers for Class 10 Maths Basic Set 4 with Solutions

Time : 3 hrs
Max. Marks : 80

General Instructions:

1. This Question Paper has 5 Sections A, B, C, D and E.
2. Section A has 20 Multiple Choice Questions (MCQs) carrying 1 mark each.
3. Section B has 5 Short Answer-I (SA-I) type questions carrying 2 marks each.
4. Section C has 6 Short Answer-II (SA-II) type questions carrying 3 marks each.
5. Section D has 4 Long Answer (LA) type questions carrying 5 marks each.
6. Section E has 3 Case Based integrated units of assessment questions (4 marks each).
7. All Questions are compulsory. However, an internal choice in 2 Qs of 2 marks, 2 Qs of 3 marks and 2 Questions of 5 marks has been provided. An internal choice has been provided in the 2 marks question of Section E.
8. Draw neat figures wherever required. Take π = 22/7 wherever required if not stated.

Section – A
Section A consists of 20 questions of 1 mark each

Question 1.
In the adjoining figure ∆APQ is similar to ∆ABC, AQ = 10 cm, BC = 3.5 cm and PQ = 7 cm, then AC is equals to

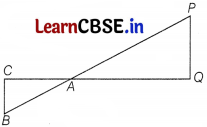
(a) 5 cm
(b) 3 cm
(c) 4 cm
(d) 2 cm
Answer:
(a) 5 cm

∆APQ ~ ∆ABC
∴ \(\frac{A Q}{A C}=\frac{P Q}{B C}\)
⇒ \(\frac{10}{A C}=\frac{7}{3.5}\)
AC = \(\frac{10 \times 3.5}{7}\)
⇒ AC = 5

Question 2.
For any two positive integers ‘a’ and ‘b’, what is the value of HCF (a, b) × LCM (a, b)? 1
(a) ab
(b) a ² b
(c) a × b
(d) a + b
Answer:
(c) a × b
Explanation: We know the relation,
HCF (a, b) × LCM (a, b) = Product of a and b.

Question 3.
The mean of the following distribution is

(a) 19.5
(b) 18
(c) 16.96
(d) 15.24
Answer:
(c) 16.96

Σ f _i x _i = 3 × 12 + 5 × 14 + 8 × 18 + 7 × 20
= 36 + 70 + 144 + 140
= 390
∴ Mean = \(\frac{\sum f_i x_i}{\sum f_i}\)
= \(\frac{390}{3+5+8+7}\)
= \(\frac{390}{23}\)
= 1696

Question 4.
Using prime factorisation method, the HCF and LCM of 210 and 175 is: 1
(a) 35,1000
(b) 34,1050
(c) 35,1050
(d) 35,1010
Answer:
(c) 35, 1050
Explanation: The prime factorisation of 210 and 175 are:
210 = 2 × 3 × 5 × 7
175 = 5 × 5 × 7
So, HCF (210, 175) = 5 × 7 = 35;
and LCM (210, 175)= 2 × 3 × 5 × 7 × 5 = 1050

Question 5.
If d _i = x _i – 20, Σf _i d _i = 300 and Σf _i = 40, then the value of \(\bar{x}\) is
(a) 20.3
(b) 32
(c) 27.5
(d) 22.9
Answer:
(c) 27.5

Given, Σf _i d _i = 300,
Σf _i = 40
and d _i = x _i – 20
We know that d _i = x _i – a
On comparing, we get a = 20
∴ \(\bar{x}\) = a + \(\left\{\frac{\Sigma f_i d_i}{\Sigma f_i}\right\}\)
= 20 + \(\frac{300}{40}\)
= 20 + \(\frac{30}{4}\)
= 20 + 7.5 = 27.5

Question 6.
By taking A = 90° and B = 30°, sin A cos B – cos A sin B is: 1
(a) 0
(b) \(\frac{\sqrt{3}}{2}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{1}{\sqrt{2}}\)
Answer:
(b) \(\frac{\sqrt{3}}{2}\)
Explanation: sin A cos B – cos A sin B
= sin 90° cos 30° – cos 90° sin 30°
= 1 × \(\frac{\sqrt{3}}{2}\) – 0 × \(\frac{1}{2}\) = \(\frac{\sqrt{3}}{2}\)

Question 7.
If 2 is a zero of polynomial f(x) = 4x ² + 4x – 4a, then the value of a is
(a) 6
(b) 2
(c) 4
(d) 8
Answer:
(a) 6

Given, polynomial is f(x) = 4x ² + 4x – 4a.
Since, 2 is a zero of the given polynomial.
∴ f(2) = 0
⇒ 4 (2) ² + 4(2) – 4a = 0
⇒ 16 + 8 – 4a = 0
⇒ 4a = 24
⇒ a = \(\frac{24}{4}\) = 6

Question 8.
The ratio of the volume of a right circular cone to that of the volume of right circular cylinder, of equal diameter and height is: 1
(a) 4 : 3
(b) 1 : 4
(c) 2 : 3
(d) 1 : 3
Answer:
(d) 1 : 3
Explanation: Volume of a right circular cone = \(\frac{1}{3}\)πr ² h
Volume of a right circular cylinder = πr ² h
So, required ratio is 1: 3.

Question 9.
The radius of a wheel is 0.25 m. The number of approximate revolutions it will make to travel a distance of 11 km, is
(a) 5000
(b) 7000
(c) 6000
(d) 1000
Answer:
(b) 7000

The distance covered in one revolution is equal to the circumference of the wheel.
∵ Circumference of wheel = 2πr
= 2 × \(\frac{22}{7}\) × 0.25
= \(\frac{11}{7}\)
∴ Number of revolutions = Distance covered by wheel / Circumference of wheel
= \(\frac{11 \times 1000}{11 / 7}\)
= 7000

Question 10.
The zeroes of the quadratic polynomial x ² + 99x + 127 are: 1
(a) both positive
(b) both negative
(c) one positive and one negative
(d) both equal
Answer:
(b) both negative
Explanation: a = 1, b = 99, c = 127

= \(\frac{-2.6}{2}\) or \(\frac{-195.4}{2}\)
= -1.3 or -97.7
Both are negative.

Question 11.
If HCF of 306 and 657 is 9, then the LCM is
(a) 19428
(b) 27352
(c) 22338
(d) None of these
Answer:
(c) 22338

Given, HCF of 306 and 657 is 9.
We know that
⇒ LCM × HCF = Product of two numbers
⇒ LCM × 9 = 306 × 657
⇒ LCM = \(\frac{306 \times 657}{9}\)
= 34 × 657 = 22338
∴ LCM of 306 and 657 = 22338.

Question 12.
The pair of linear equation is x + 3y – 6 = 0, 2x + 17y – 13 = 0 is: 1
(a) inconsistent
(b) parallel lines
(c) consistent
(d) data insufficient
Answer:
(c) consistent
Explanation: Here, a ₁ = 1, b ₁ = 3, c ₁ = -6
a ₂ = 2, b ₂ 17, c ₂ = – 13
Now, \(\frac{a_1}{a_2}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{3}{17}\) and \(\frac{c_1}{c_2}=\frac{6}{13}\)
⇒ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)
∴ Given pair of linear equations have a unique solution. Hence, given pair of linear equations is consistent.

Question 13.
If tan (3x + 30°) = 1, then the value of x is
(a) 3°
(b) 5°
(c) 10°
(d) 0°
Answer:
(b) 5°

We have, tan(3x + 30°) = 1
⇒ tan(3x + 30°) = tan 45°
[∵ tan 45° = 1]
⇒ 3x + 30° = 45°
⇒ 3x = 45° – 30° = 15°
⇒ x = 5°

Question 14.
Tony and Monu go to an ice-cream parlour where they find 5 different varieties of ice creams. If they order one ice-cream each. The probability that they both order the same variety of ice creams is: 1
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{3}\)
(d) \(\frac{1}{5}\)
Answer:
(d) \(\frac{1}{5}\)
Explanation: Total number of possible outcomes = 5 × 5 = 25
Let the five different varieties of icecreams be a, b, c, d and e.
So, favourable outcomes are {(a, a), (b, b), (c, c), (d, d), (e, e)}i.e., 5
∴ Required probability = \(\frac{5}{25}\) = \(\frac{1}{5}\)

Question 15.
If the LCM and HCF of two non-zero positive numbers are equal, then the numbers must be
(a) prime
(b) coprime
(c) composite
(d) equal
Answer:
(d) equal

Given, LCM and HCF are equal.
Let two non-zero positive numbers are p and q.
Then, HCF(p, q) = LCM (p, q) [given]
Let HCF (p, q) = k
⇒ p = ka
and q = kb
where, a and b are natural numbers,
∵ HCF × LCM = Product of numbers
k × k = ka × kb
⇒ a × b = 1
∴ a = b = 1, as they are natural numbers.
Hence, p = q or the number must be equal.

Question 16.
A stopwatch was used to find the time that it took a group of students to run 100m. 1

Time (in sec)	Number of students
0 – 20	8
20 – 40	10
40 – 60	13
60 – 80	6
80 – 100	3

What will be the upper limit of the modal class? 1
(a) 20
(b) 40
(c) 60
(d) 80
Answer:
(c) 60
Explanation: Modal class = 40 – 60, therefore upper limit = 60.

Question 17.
The prime factorization of 352 is
(a) 2 ⁸
(b) 2 ⁶ × 11
(c) 2 ⁵ × 11
(d) 2 ⁶ × 7
Answer:
(c) 2 ⁵ × 11

We have, 352 = 2 × 2 × 2 × 2 × 2 × 11
∴ 352 = 25 × 11

Question 18.
A rolling pin is made by joining three cylindrical pieces of wood, as shown in the figure:

Assuming that there is no wastage of wood, the volume of wood used in making the rolling pin is: 1
(a) 64π cm ³
(b) 280π cm ³
(c) 480π cm ³
(d) 544π cm ³
Answer:
(d) 544π cm ³
Explanation: For the bigger cylinder:
r ₁ = 4 cm
h ₁ = 30 cm
For the two smaller cylinders:
r ₂ = \(\frac{4}{2}\) = 2 cm,
h ₂ = 8 cm
Now, Volume of wood used = Volume of the pin
= Volume of bigger cylinder + ( 2 × Volume of smaller cylinder)
= πr ₁ ² h ₁ + 2 × πr ₂ ² h ₂
= π × (4) ² × 30 + 2 × π × (2) ² × 8
= 480π + 64π
= 544π cm ³

Directions: In question number 19 and 20, a statement of Assertion (A) is followed by a statement of Reason (R). Choose the correct option.

Question 19.
Assertion (A) : A coin is tossed 30 times and head appears 20 times. Then, the probability of getting a tail is 1 / 3.
Reason (R) : Probability of happening of an event
Number of trials in which = the event happened / Total number of trials
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation, of Assertion (A).
(b) Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
(c) Assertion (A) is true but Reason (R) is false.
(d) Assertion (A) is false but Reason (R) is true.
Answer:
(a) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation, of Assertion (A).

Total number of times in which tail appeared = 30 – 20 = 10
∴ Probability of getting a tail = \(\frac{10}{30}=\frac{1}{3}\)
So, the given Assertion (A) is true.
Also, the given Reason (R) is also true and it is the correct explanation of Assertion (A).

Question 20.
Assertion (A): If the probability of the occurence of an event is \(\frac{3}{7}\), then the probability of its non-occurrence is \(\frac{5}{7}\).
Reason (R): P(A) + P(\(\overline{\mathbf{A}}\)) = 1, when P(\(\overline{\mathbf{A}}\)) is a complement of P(A). 1
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A)
(c) Assertion (A) is true but reason (R) is false.
(d) Assertion (A) is false but reason (R) is true.
Answer:
(d) Assertion (A) is false but reason (R) is true.
Explanation: For an event A, the
P(A) + P(\(\overline{\mathrm{A}}\)) = 1
Here, P(A) = \(\frac{3}{7}\)
Then, P(\(\overline{\mathrm{A}}\)) = 1 – \(\frac{3}{7}\)
= \(\frac{4}{7}\)

Section – B
Section B consists of 5 questions of 2 marks each.

Question 21.
In the given figure, a circle is inscribed in a ∆ABC. If AB = 10 cm BC = 8 cm, and AC = 12 cm, then find the lengths of BM, CN and AL.

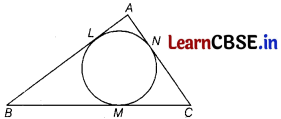
Answer:
We know that the lengths of the tangents drawn from an external point to a circle are equal.
Let AL = AN = x ;
BL = BM = y ;
CM =CN = z
Now, AL+BL = AB, x + y = 10 ……….(i)
BM + CM = BC, y + z = 8 ………….. (ii)
CN+AN = AC,z + x = 12 ……………(iii)
On subtracting Eq. (ii) from Eq. (iii), we get
x – y = 4 …………. (iv)
On solving Eqs. (i) and (iv), we get
x = 7, y = 3
Now, substituting y = 3 in Eq. (ii), we get
z = 5
BM = y = 3 cm,
CN = z = 5 cm
and AL = x = 7 cm

Question 22.
Find the zeros of 3x ² – x – 4. 2
Answer:
Let p(x) = 3x ² – x – 4
= 3x ² – 4x + 3x – 4
= x(3x – 4) + 1 (3x – 4)
= (3x – 4) (x + 1)
3x – 4 = 0, x + 1 = 0, x = \(\frac{4}{3}\), x = -1
So, the two zeros of 3x ² – x – 4 are \(\frac{4}{3}\) and -1.

Question 23.
If the 3rd and 9th terms of an AP are 4 and – 8 respectively, then which term of this AP • is zero?
Answer:
Let a be the first term and d be the common difference of an AP.
∵ The n th term of an AP is a _n = a + (n – 1) d
∴ a ₃ = a + 2d
⇒ a + 2d = 4
[∵ a ₃ = 4 (given)] …………(i)
and a ₉ = a + 8d
⇒ a + 8d = – 8
[∵ ag = – 8 (given)]… (ii)
On subtracting Eq. (i) from Eq. (ii), we get
6d = – 12
⇒ d = \(\frac{- 12}{6}\) = – 2
∴ From Eq. (i),
a + 2 × (- 2) = 4
⇒ a – 4 = 4
⇒ a = 4 + 4 = 8
Let the nth term of an AP is zero.
Then, a _n = 0
⇒ a + (n – 1) d = 0
⇒ 8 + (n – 1) (- 2) = 0
⇒ (n – 1) (- 2) = – 8
⇒ n – 1 = \(\frac{- 8}{- 2}\) = 4
⇒ n = 4 + 1 = 5
Hence, 5th term of an AP is zero.

Question 24.
Find the area of the shaded region. 2

Answer:
Area of the shaded region = Area of a semi-circle of radius 14 cm + 2 × Area of a semi-circle of radius 7 cm.
= (\(\frac{\pi}{2}\)(14) ² + 2 × \(\frac{\pi}{2}\)(7) ² )sq. cm
= (\(\frac{1}{2}\) × \(\frac{22}{7}\) × 14 × 14 + \(\frac{22}{7}\) × 7 × 7)sq. cm
= (308 + 154) sq. cm
= 462 sq. cm.

Question 25.
Two dice are thrown simultaneously. Find the probability of getting a multiple of 2 on one die and a multiple of 3 on the other die.
Answer:
Here, two dice are thrown, so possible outcomes are
(1.1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2.1), (2,2), (2, 3), (2, 4), (2, 5), (2, 6)
(3.1), (3,2), (3, 3), (3, 4), (3, 5), (3, 6)
(4.1), (4,2), (4, 3), (4, 4), (4, 5), (4, 6)
(5.1), (5,2), (5, 3), (5, 4), (5, 5), (5, 6)
(6.1), (6,2), (6, 3), (6, 4), (6, 5) and (6, 6)
∴ Total number of outcomes = 36
Let E = Event of getting a multiple of 2 on one die and a multiple of 3 on the other die.
Here, multiples of 2 are 2, 4 and 6 and multiples of 3 are 3 and 6.
So, favourable outcomes for event E are (2, 3), (4, 3), (6,3), (2,6), (4, 6), (6, 6), (3,2), (3,4), (3,6), (6,2) and (6, 4).
∴ Number of outcomes favourable to E = 11
∴ Required probability = P(E)
= \(\frac{\text { Number of favourable outcomes to } E}{\text { Total number of outcomes }}\)
= \(\frac{11}{36}\)

Or

Suppose you drop a die 5 m at random on the rectangular region shown in figure. What is the probability that it will land inside the circle of diameter 2 m?

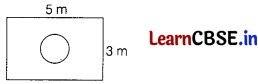
Answer:
Area of rectangle = 5 × 3 = 15 m ²
and area of circle of radius 1 m = π (1) ²
= π m ²
[∵ diameter = 2m
⇒ radius = \(\frac{2}{2}\) = 1 m]
Now, probability that the die land inside the circle = \(\frac{\pi}{15}\)

Section – C
Section C consists of 6 questions of 3 marks each

Question 26.
On a morning walk, three girls step off together and their steps measure 40 cm, 42 cm and 45 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps? 3
Answer:
Required minimum distance
= LCM (40, 42, 45)
∵ 40 = 2 × 2 × 2 × 5 i.e., 2 ³ × 5
42 = 2 × 3 × 7
45 = 3 × 3 × 5 i.e., 3 ³ × 5
∴ LCM (40, 42, 45) = 23 × 32 × 5 × 7
= 2520 cm

Question 27.
In the given figure, PP’ and QQ’ are the two common tangents of the two circles. Show that PP’ = QQ’.

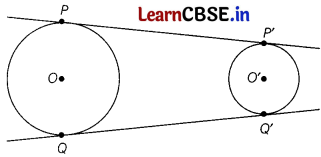
Answer:
Produce PP’ and QQ’ to meet at point R (say)

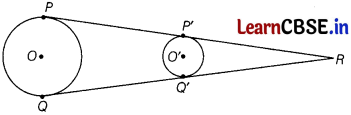
[∵ R is an external point and lengths of tangents drawn from an external point to a circle are equal]
⇒ RP’ + P’P = RQ’ + Q’Q
⇒ P’P = Q’Q
[∵ RP’ = RQ’]

Question 28.
In the figure, sectors of two concentric circles of radii 7 cm and 3.5 cm are shown.

Find the area of the shaded region. 3
Answer:
Area of the shaded region
= Area of the sector of radius 7 cm. – Area of the sector of radius 3.5 cm
= \(\frac{30^{\circ}}{360^{\circ}}\)π(7) ² – \(\frac{30^{\circ}}{360^{\circ}}\)π(3.5) ² ) sq .com
= \(\frac{30}{360}\) × \(\frac{22}{7}\) × (49 – 12.25) sq. cm
= 9.625 sq. cm

Question 29.
In ∆ABC, ∠B = 90° and BD ⊥ AC. If AC = 10 cm and AD = 4 cm, then find the value of BD.
Answer:
Given, AC = 10 cm,
AD = 4 cm
CD = AC – AD
= 10 – 4 = 6 cm

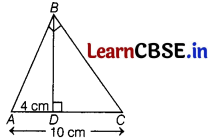
In ∆ABC and ∆ADB
∠BAC = ∠BAD
∠ABC = ∠ADB [each 90° angle]
∴ ∆ABC ~ ∆ADB
[by AA similarity criterion] …………….. (i)
In ∆ABC and ∆BDC,
∠ABC = ∠BDC [each 90° angle]
∠ACB = ∠BCD
∴ ∆ABC ~ ∆BDC
[by AA similarity criterion] ……………. (ii)
From Eqs. (i) and (ii),
∆ADB ~ ∆BDC
∴ \(\frac{B D}{C D}=\frac{A D}{B D}\)
⇒ BD ² = AD . CD
= 4 × 6
= 24 cm
⇒ BD = 2√6 cm

Question 30.
In the given figure, DE || AQ and DF || AR. Prove that EF || QR. 3

Answer:
Given: In ΔPQR, DE || AQ and DF || AR
To prove: EF || QR

Question 31.
Solve for x, \(2\left(\frac{2 x+3}{x-3}\right)-25\left(\frac{x-3}{2 x+3}\right)\) = 5.
Answer:
Given \(2\left(\frac{2 x+3}{x-3}\right)-25\left(\frac{x-3}{2 x+3}\right)\) = 5
Let \(\frac{2 x+3}{x-3}\) = y ……………(i)
Then, \(\frac{x-3}{2 x+3}=\frac{1}{y}\) = \(\frac{1}{y}\)
Therefore, the given equation reduces to
2y – 25 \(\frac{1}{y}\) = 5
⇒ 2y ² – 25 = 5y
⇒ 2y ² – 5y – 25 = 0
⇒ 2y ² – 10y + 5y – 25 = 0
⇒ 2y (y – 5) + 5 (y – 5) = 0
⇒ (y – 5) (2y + 5) = 0
⇒ y = 5 or y = \(-\frac{5}{2}\)
Now, on putting y = 5 in Eq. (i), we get
\(\frac{2 x+3}{x-3}=\frac{5}{1}\)
⇒ 5x – 15 = 2x + 3
⇒ 3x = 18
⇒ x = 6
Again, on putting y = – \(\frac{5}{2}\) in Eq. (i), we get
\(\frac{2 x+3}{x-3}=-\frac{5}{2}\)
⇒ – 5x + 15 = 4x + 6
∴ 9x = 9
⇒ x = 1
Hence, the values of x are 1 and 6.

Section – D
Section D consists of 4 questions of 5 marks each

Question 32.
Mr. Sharma and Mr. Arora are family and they decided to go for a trip. For the trip they reserved their rail tickets. Mr. Arora has not taken a half ticket for his child who is 6 years old whereas Mr. Sharma has taken half tickets for his two children who are 6.5 years and 8 years old. A railway half ticket costs half of the full fare but the reservation charges are the same as on a full ticket. Mr. and Mrs. Arora paid ₹ 1700, while Mr. and Mrs. Sharma paid ₹ 2700. Find the full fare of one ticket and the reservation charges per ticket.
OR
Rajiv walks and cycles at uniform speeds. When he walks for 2 hrs and cycles for 1 hr, distance travelled is 24 km. When he walks for 1 hr and cycles for 2 hrs, distance travelled is 39 km. Find his speed of walking and cycling. If he walked and cycled for equal to time in 3 hrs how much distance does he cover? 5
Answer:
Let the full fare of one ticket for a trip be ₹ x, then the railway half fare of one ticket for a trip be ₹ \(\frac{x}{2}\).
Let the reservation charges per ticket be ₹ y.
According to the given conditions:
x + y + x + y= 1700 (Amount paid by Mr. and Mrs. Arora)
⇒ 2x + 2y = 1700 …….. (i)
and (x + y) + (x + y) + (\(\frac{x}{2}\) + y) + (\(\frac{x}{2}\) + y) = 2700
(Amount paid by Mr. and Mrs. Sharma and their two children)
⇒ 3x + 4y = 2700 ….. (ii)
From (i), y = \(\frac{1700-2 x}{2}\) …………. (iii)
Substituting value of y from (iii) in (ii), we get
3x + 4(\(\frac{1700-2 x}{2}\)) = 2700
⇒ 3x + 3400 – 4x = 2700
⇒ x = 700
Now, putting x = 700 in (iii), we get
y = \(\frac{1700-2(700)}{2}\)
⇒ y = \(\frac{1700-1400}{2}\)
= \(\frac{300}{2}\) = 150
Hence, the full fare of one ticket = ₹ 700 and the reservation charges = ₹ 150 per ticket.
OR
Let the speed of walking be x km/hr and the speed of cycling be y km/hr.
According to the question,
2x + y = 24 ……….. (i)
and x + 2y = 39 ………. (ii)
Multiplying (i) by 2, we get 4x + 2y = 48 ……… (iii)
Subtracting (ii) from (iii), we get
3x = 9
⇒ x = 3
Putting the value of x in (i), we get
2(3) + y = 24
⇒ y = 24 – 6 = 18
∴ Speed of walking is 3 km/hr and speed of cycling is 18 km/hr.
When Rajiv walked and cycled for equal time.
Distance covered = 3 × 1.5 + 18 × 1.5
= 4.5 + 27 = 31.5 km

Question 33.
From the top of a 7 m high building the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45° . Determine thc height of the tower.
Answer:
Let AD = 7m be the height of the building
and BC = h be the height of the cable tower.
From the top of the building D, the angles of elevation and depression are ∠CDE = 60° and ∠EDB = 45°, respectively.
From the point D, draw a line DE || AB,
Then, ∠EDB = ∠48° = 45° (alternate angles)

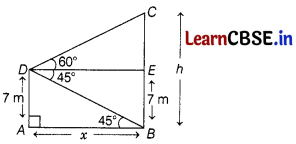
Also, let AB = DE = x be the distance between building and tower.
In right angled ∆BAD,
tan 45° = \(\frac{P}{B}=\frac{A D}{A B}\)
1 = \(\frac{7}{x}\)
[∵ tan 45° = 1]
⇒ x = 7 m
and in right angled ∆CED,
tan 60° = \(\frac{C E}{D E}\)
= \(\frac{C B-B E}{A B}\)
[∵ CE = CB – BE]
⇒ √3 = \(\frac{h-7}{x}\)
[∵ tan 60° = √3]
⇒ h – 7 = x√3
⇒ h = x√3 + 7
⇒ h = 7√3 + 7 [from Eq.(i)]
⇒ h = 7(√3 + 1) m
Hence, the height of the tower is 7 (√3 + 1) m.

Question 34.
In the given figure, O is the centre of circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30°, prove that BA : AT = 2 :1. 5

Answer:
Given: O is the centre of circle and TP is the tangent to circle and ∠PBT = 30°.

To prove: \(\frac{\mathrm{BA}}{\mathrm{AT}}=\frac{2}{1}\)
Construction: Join OP
Proof: ∠BPA = 90° [Angle in a semi circle]
In ΔBPA, ∠BPA + ∠PBA + ∠BAP = 180° [Angle sum property]
⇒ 90° + 30° + ∠BAP = 180°
⇒ ∠BAP = 60°
Also, ∠OPT = 90°
and OP = OA
(Radii of same circle) ……. (i)
∠OAP = ∠OPA
= 60° ….. (ii)
⇒ ∠APT = 90° – 60°
= 30°
Now, ∠OAP + ∠PAT = 180° [Linear pair]
⇒ 60° + ∠PAT = 180° [Using (ii)]
⇒ ∠PAT = 120°
In ΔPAT, ∠PAT + ∠APT + ∠PTA = 180°
⇒ 120° + 30° + ∠PTA = 180°
⇒ ∠PTA = 30°
⇒ PA = AT …… (iii)
Also, in ΔOAP,
∠AOP = 180° – 60° – 60° = 60°
∴ ∠AOP = ∠OPA
⇒ PA = OA …… (iv)
Hence, PA = AT = OA = OP
[Using (i), (iii) and (iv)]
Now, BA = BO + OA = 20A [∵ OA = OB]
⇒ BA = 2AT [∵ OA = AT]
⇒ \(\frac{\mathrm{BA}}{\mathrm{AT}}=\frac{2}{1}\)

Question 35.
In the given figure, AD is the bisector of ∠BAC of AABC.

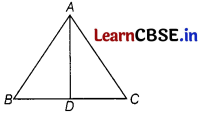
Prove that \(\frac{B D}{D C}=\frac{A B}{A C}\).
Answer:
Given : In the given figure, AD is the bisector of ∠BAC of AABC.
∴ ∠BAC = ∠ CAD
To prove : \(\frac{B D}{D C}=\frac{A B}{A C}\)
Construction : Now, draw CT || DA to meet BA produced at A.

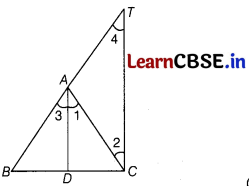
Proof CT|| DA
and transversal AC intersects them.
∴ ∠1 = ∠2 [alternate interior angles] ………….. (i)
Also, CT || DA
and transversal BT intersects them.
∴ ∠3 = ∠4 [corresponding angles] ……………. (ii)
But ∠1 = ∠3 [given]
⇒ ∠1 = ∠4 [from Eq. (ii)] …………… (iii)
From Eqs. (i) and (iii), we get
∠2 = ∠4
⇒ AT = AC
[since, sides opposite to equal angles of a triangle are also equal] ……………… (iv)
In ∆BCT,
AD || CT
∴ \(\frac{B D}{D C}=\frac{A B}{A T}\) [by BPT)
⇒ \(\frac{B D}{D C}=\frac{A B}{A C}\) [from Eq. (iv)]
DC Hence proved.

Section – E
Case study-based questions are compulsory

Question 36.
Rishu is riding in a hot air balloon. After reaching point P, he spots a car parked at B on the ground at an angle of depression of 30°. The balloon rises further by 50 meters and now he spots the same car at an angle, of depression of 45° and a lorry parked at B’ at an angle of depression of 30°. (Use √3 . = 1.73)

The measurement of Rishu facing vertically is the height. Distance is defined as the measurement of car/lorry from a point in a horizontal direction. If an imaginary line is drawn from the observation point to the top edge of the car/lorry, a triangle is formed by the vertical, horizontal and imaginary line.

Based on the above information, answer the following questions:
(A) If the height of the balloon at point P is ‘h’m and distance AB is V m, then find the relation between V and ‘h’. 1
(B) What is the relation between the height of the balloon at point P and distance AB? 1
(C) Find the height of the balloon at point P and the distance AB on the ground.
OR
Find the distance B’B on the ground. 2
Answer:

(A) In ΔAPB,
tan 30° = \(\frac{A P}{A B}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{h}{x}\)
⇒ x = \(\sqrt{3} h\)

(B) In ΔAP’B
tan 45° = \(\frac{A P^{\prime}}{A B}\)
⇒ AB = AP’
⇒ x = h + 50 …….. (ii)

(C) On solving equation obtained in (i) and (ii), we get
\(\sqrt{3} h\) = h + 50
⇒ h(√3 – 1) = 50
⇒ h = \(\frac{50}{0.732}\) = 68.5
In ΔAPB,
tan 30° = \(\frac{A P}{A B}\)
⇒ AB = \(\frac{\mathrm{AP}}{\tan 30^{\circ}}\)
= \(\frac{68.25}{\frac{1}{\sqrt{3}}}\)
= 68.25 × 1.732
= 118 m
OR
In ΔAP’B’
tan 30° = \(\frac{\mathrm{AP}^{\prime}}{\mathrm{AB}^{\prime}}\)
\(\frac{1}{\sqrt{3}}=\frac{68.25+50}{A B^{\prime}}\)
⇒ AB’ = 118.25 × 1.732
= 204.809
BB’ = AB’-AB
= 204.809 – 118
= 86.80 = 87 m

Question 37.
A teacher of class X drew the three graphs of quadratic polynomials on the board as shown below.

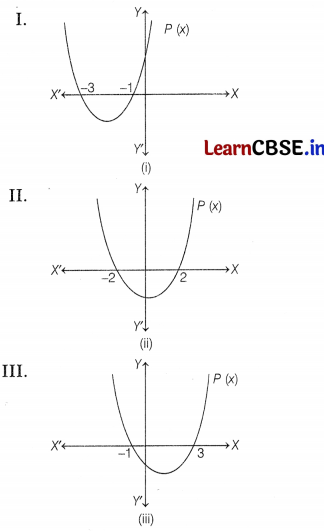
Answer the following questions which are based on the above graphs.

(i) Write the zeroes of polynomial P(x) in graph I.
Answer:
From the graph I, we have
Zeroes of P(x) = – 3, – 1

(ii) Write the zeroes of polynomial P(x) in graph II.
Answer:
From the graph II, we have
Zeroes of P(x) = – 2, 2

(iii) Write the polynomial P(x) for graph (I).
Answer:
In graph I, sum of zeroes = – 3 -1 = – 4
and product of zeroes = (- 3) (- 1) = 3
∴ Polynomial P(x) will be x ² – (Sum of zeroes) x + Product of zeroes = x ² + 4x + 3

Or
Find the value of (a + b) for which p(x) = x2 + ax – b in graph III. (2)
Answer:
From the graph III, we have
Zeroes of p(x) = – 1, 3
Sum of zeroes = 2 = \(\frac{-a}{1}\)
⇒ a = – 2
and product of zeroes = – 3 = – b
⇒ b = 3
∴ a + b = – 2 + 3 = 1

Question 38.
Delhi public school society has so many schools in different cities of India. One of the branches of Delhi Public School is in Ghaziabad. In that school thousands of students study in the classroom.

Out of them one of the boy is standing in the ground having coordinates (4, 1) facing ‘ towards east. He moves 4 units in straight line then take right and moves 3 units and stop. Now he is at his home.
The representation of the given situation on the coordinate axes is show below.

Based on the above information, answer the following questions:
(A) What is the shortest distance between his school and house?
OR
Suppose point D divide the line segment AB in the ratio 1: 2, then find the coordinate of D. 2
(B) If we draw perpendicular lines from
points A and B to the x-axis, find, the region covered by these perpendicular lines. 1
(C) Find the image of point C w.r.t. x-axis.l
Answer:
(A) From the given figure, shortest distance between school and house = AB
= \(\sqrt{(8-4)^2+(4-1)^2}\)
[from distance formula]
= \(\sqrt{4^2+3^2}=\sqrt{16+9}\)
= \(\sqrt{25}\) = 5 units
∴ Shortest distance = 5 km[l unit = 1 km]
OR
By using internal section formula.

(B) When, we draw perpendicular lines from the points, a rectangle is formed.
∴ Area of covered region
= l × b
= 4 × 1 = 4 sq units

(C) The image of a point C w.r.t. X-axis is (8,-4).